基于改进KH-ANFIS 的海洋溶菌酶发酵过程软测量

朱湘临，王 森，王 博

(江苏大学 电气信息工程学院,江苏 镇江 212000)

0 引言

与工业生产中普遍应用的蛋清溶菌酶相比，经嗜低温海洋细菌发酵之后得到的海洋溶菌酶(ML,marine lysozyme)具有更好的抗氧化、耐低温高压等生物特性，在生物工程领域、医药制造和食品包装方面得到了广泛的应用[1-3]。但是ML发酵过程十分复杂，发酵过程中某些关键生物参量(菌体浓度、基质浓度、相对酶活)在线测量十分困难[4-5]。目前发酵的关键参量常用的测量方法是离线测量的方法，但是发酵过程的高度时变性和大滞后性将会导致离线测量误差较大，且操作过程复杂的离线测量污染较为严重，不能够及时反映发酵过程当前状态。采用软测量技术[6-9]是解决该类问题的有效方式之一。

模糊神经网网络[10](FNN，fuzzy neural network)兼备神经网络以及模糊推理的优势，具有很强的推理能力和自适应性能。其强大的自适应能力，在复杂非线性的微生物发酵过程软测量建模中得到了广泛地应用。何朝峰[11]等人将FNN应用于发酵过程关键参数的软测量建模方法中，有效的提高了收敛速度，发酵关键参数的输出超调量得到了有效的控制，同时对其时变特性具有较好的鲁棒性。王华国[12]等人针对发酵过程中关键生物参量难以在线检测的问题提出了一种基于粒子群优化算法与FNN相结合的软测量方法，具有收敛速度快的优点。自适应模糊神经网络[13-15,17](ANFIS,adaptive fuzzy neural network)作为FNN的一种，其进一步加强了神经网络的推理功能，改善了传统神经网络易于陷入局部最优的欠缺点，在复杂非线性系统软测量中得到了广泛的应用。但是在ANFIS软测量建模过程中，存在自适应调节过程计算量复杂，在线修正权值过度等问题。而在ML实际发酵过程中，其过程参数随着时间的推移易发生改变，ANFIS模型的权值过度修正也将导致软测量模型精度的下降，难以对ML实际发酵过程进行准确预测。因此需要采用一些方法对ANFIS软测量模型进行优化改进。基于此，提出了一种基于改进的KH-ANFIS软测量模型的研究方法，将所提出的方法用于ML发酵过程菌体浓度的预测中，利用实际发酵过程中采集的发酵样本参数验证了该方法的有效可行性。

1 算法描述

1.1 自适应模糊神经网络

作为一种将人工神经网络和模糊推理结合的神经模糊推理系统，ANFIS网络结构如图1所示。

图1 ANFIS网络结构

模型共分为5层，详细的功能如下：

第一层：模糊化处理层，主要作用是确定过程数据输入量的隶属度函数，其输出函数为：

(1)

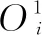
第二层：节点固定层，主要功能是对输入信号进行乘法运算，计算出对应规则的可信度，其输出函数表示为：

(2)

式中，ωi表示为自适应节点i的对应规则的适应度值。

第三层：去模糊化层，目的是对自适应节点i的规则适应度值进行归一化操作，其输出函数：

(3)

第四层：节点参数输出层，主要作用是利用后件参数对自适应节点i对应的规则输出进行计算，得出其对最后结果的影响，其具体函数表达：

(4)

式中，{pi,qi,ri}为自适应节点i的参数集合，统称为ANFIS网络的后件参数。

第五层：节点变量输出层，目的是对输入的模糊化参数进行退模糊化操作，通过计算得出所有过程数据输入变量对应的总输出，函数表达为：

(5)

通过分析可知，ANFIS软测量模型具有FNN的优点，但仍然存在着一些不足。由于反馈网络存在的计算量大，参数过度修正等问题，不能很好地提高预测精度，因此本文提出了一种优化ANFIS软测量模型的方法，使得最终的预测精度进一步提高。

1.2 改进磷虾群算法

1.2.1 磷虾群算法

磷虾群算法(KH，krill herd algorithm)[18-23]是一种模拟南极海洋中磷虾群个体的智能算法，其目的利用磷虾不同个体之间的互相合作和信息交流来完成在解空间内的迭代寻优，最终得到算法的最优解。

算法中，磷虾群的位置活动主要是由磷虾个体觅食活动导致的个体响应以及磷虾不同个体之间的最短相邻感应距离来决定的。而每一个磷虾个体的位置变化主要是由三种活动组成：不同个体互相感应导致的磷虾个体诱导游动，磷虾个体的随机扩散运动以及个体的觅食活动。其具体表达如下：

(6)

式中，Ni表示为磷虾个体i在其余个体诱导下产生的个体游动，Fi代表磷虾个体i的觅食活动，Di是磷虾个体i的随机扩散运动。其中磷虾个体i的当前食物位置以及之前的觅食经验组成了个体的觅食活动Fi，具体公式表达如下：

(7)

(8)

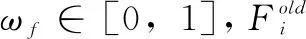
造成磷虾群在不断的随机游动活动中保持一定的聚集密度的原因是因为磷虾群中不同个体之间存在着一定的信息交换和相互感应。在解空间的相邻集合中，当磷虾个体i与磷虾群中其余个体之间的距离在个体i的感知范围之内，则该磷虾个体的移动方向为感知范围内距离最短的其他个体方向，其具体公式如下：

(9)

(10)

磷虾个体的扩散游动主要由两种因素决定，具体表达式如下：

Di=Dmaxδ

(11)

式中，Dmax是该个体随机扩散时的最大扩散速度；δ代表该个体进行随机扩散时的方向矢量，数值是[-1,1]的一个随机数。

个体利用自身的觅食活动，随机扩散以及个体感知范围内的游动来对其本身参数进行不断的更新，从而导致解空间内该磷虾个体的位置不断的变换，直至获得最优解，其在Δt时间间隔内位置变换的具体公式如下：

(12)

式中，Δt表示速度向量的缩放因子；Ct是步长缩放因子，Ct∈ [0，1]；NV为磷虾群中个体数量，Uβmax,Uβmin分别为其最大值和最小值。

1.2.2 基于自适应莱维飞行的KH算法

在传统的KH算法中，由于其自身的随机扩散游动将导致种群多样性下降，前期的全局搜索能力弱，因此提出利用自适应莱维飞行策略[24-25]来对其随机扩散游动进行改进的研究，通过前期全局搜索范围的扩大来增强算法在迭代过程前期的全局搜索能力；同时针对算法后期因种群多样性的下降导致的算法陷入局部最优解的问题，提出利用跳变技术(HOT)来使得算法跳出局部最优的研究方法。其具体流程如图2所示。

图2 改进磷虾群算法流程图

在传统KH算法中，磷虾群个体的随机扩散游动主要决定因素是最大扩散速度以及随机扩散方向矢量，根据标准KH算法中随机扩散公式可知，决定扩散游动方向的随机扩散方向矢量为随机数，这会造成算法在前期的全局搜索能力差的问题，通过莱维飞行策略来代替随机扩散游动方程，将式(11)改为：

L(s)～|s|-1-β，0<β<2

(13)

式中，s是随机步长，其具体表达式：

(14)

式中，μ，ν服从正态分布：

(15)

(16)

式中，τ表示积分运算；β=1.5；即σμ=0.69。

通过自适应莱维飞行策略对KH算法中的随机扩散运动进行改进，从而在算法前期达到全局搜索能力提高的效果。

针对KH算法后期因种群多样性下降造成的陷入局部最优解的问题，提出了利用HOT技术对算法位置更新公式进行改进的研究，具体表达式如下：

(17)

式中，θ为[-1,1]均匀分布的随机数。

在KH算法中加入跳变操作，当磷虾群个体陷入局部最优解时，利用位置更新公式(16)对磷虾个体i的位置重新计算，使得KH算法跳出局部最优解。

2 海洋溶菌酶软测量模型

将ML发酵获得的过程数据按照4∶4∶2的比例分为训练数据、测试数据和验证数据。利用训练数据得到初始ANFIS网络模型，并利用改进的KH算法对初始ANFIS网络模型前件参数进行动态优化，生成最优ANFIS 网络模型结构，并作为软测量最终预测模型。通过验证数据检测软测量预测模型的泛化能力并计算预测误差，并利用该模型对海洋溶菌酶发酵过程进行在线跟踪，实现发酵过程的控制。

2.1 辅助变量的选择

建立精确有效的软测量模型，首先要选择合适的辅助变量，在海洋溶菌酶发酵过程，能够利用仪器在线检测的主要环境参量有：通氧量DO、发酵罐压力p、发酵温度T、发酵液体积V、电机转速U、葡萄糖流加速率C、pH、光照强度E、氨水流加速率η等。

为获得能够准确反应海洋溶菌酶菌体浓度变化数据，采用一致关联度法[26]对主要环境参量进行选择，选出与菌体浓度关联度最高的环境参量作为软测量模型辅助参量，表1 为各发酵过程主要环境参量与菌体浓度关联度的具体数值。

表1 环境变量与关键参量的关联度

根据表1中的关联度值，选择与海洋溶菌酶菌体浓度关联度最高的发酵液pH、通氧量DO、发酵温度T、电机转速U作为辅助变量。

2.2 HLKH-ANFIS的软测量建模

采集离线数据训练构建基于HLKH-ANFIS的海洋溶菌酶菌体浓度软测量模型，利用训练数据对模型进行训练过程中，采用改进的KH算法对初始ANFIS网络反馈环节中的前件参数和聚类中心范围进行动态寻优，然后利用测试数据对训练好的模型进行测试，从而验证模型的预测能力。

算法具体步骤如下：

1) 首先选择样本数据，将数据划分为训练集和测试集，并对数据进行预处理，利用预处理之后的数据确定ANFIS网络结构，设定网络的前件参数。

2)初始化KH算法的相关参数，如最大迭代次数Nmax，种群数量n，搜索变量的个数NV等。

3)使用训练样本进行训练，并用网络的均方误差作为算法的适应度。

4)利用HLKH算法进行迭代搜索和位置更新，根据适应度最小原则选择最优的个体。

5)判断迭代次数是否达到最大迭代次数，若达到最大迭代次数，则结束迭代，否则，返回步骤4)，重新进行迭代。

6)迭代结束后，选择适应度最佳的模型参数建立ANFIS软测量预测模型，最后得到基于HLKH-ANFIS的海洋溶菌酶发酵菌体浓度软测量模型。

3 仿真实验验证

实验所需海洋溶菌酶发酵过程数据由江苏大学发酵控制系统平台提供，发酵罐所用型号为RT—100L—Y，利用标准发酵工艺所用培养基进行分批发酵，设置发酵罐内温度T=32℃；设定发酵搅拌轴转速n=400 r/min；罐内氧气含量设定为35%～40%；罐内pH=7.3；经实验可得海洋溶菌酶发酵时长为70 h；按照发酵控制平台测得的周期数据，取用10批次数据，其中训练集选用4 个批次数据，测试集选用4个批次数据，剩余2个批次实验数据作为软测量模型的验证集。首先对平台获得数据进行预处理(辅助变量的选择)后，利用上述的软测量建模方法对数据进行训练，然后采用测试集中的4批数据对模型的拟合程度以及预测精度进行验证，最后选择均方根误差(RMSE)和最大绝对误差(MAXE)对建立的模型的预测精度进行评价。

(18)

(19)

为了验证上述方法对海洋溶菌酶发酵过程软测量建模的可行性，采用基于改进KH-ANFIS软测量建模方法建立海洋溶菌酶发酵过程菌体浓度软测量模型。选用传统的KH-ANFIS作为对比，设定磷虾种群个数n=50，算法最大迭代次数Nmax=2 000，搜索变量NV=90,搜索范围[-10,10],设定迭代终止误差条件ε=0.03。由于所建模型具有4个输入变量和一个输出变量，ANFIS网络具有4个输入节点和1个输出节点，设定隐含节点数为7。预测结果仿真如图3所示。

图3 仿真效果图

对比图3中菌体浓度仿真效果图可知：基于HLKH-ANFIS的软测量预测模型比基于KH-ANFIS的预测模型更加接近真实值，即基于HLKH-ANFIS的软测量模型的拟合程度更高，预测效果更好。为了直观体现两种模型的预测精度，得出两种模型的软测量误差曲线如图4所示。

图4 预测模型误差

根据图4中两种软测量误差曲线可以得出：改进KH-ANFIS软测量模型预测误差比传统的KH-ANFIS模型的预测误差要小，拟合程度也较高。

表2为两种模型预测结果的误差对比。由表中误差数据可知，改进KH-ANIFS模型的均方根误差为0.246 2,其最大绝对误差也要低于传统的KH-ANFIS模型，表明了模型的稳定性较好且预测精度更高。

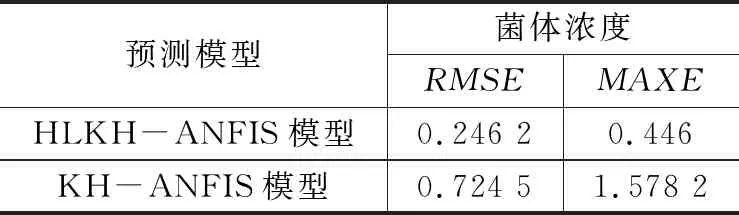
表2 预测模型仿真效果对比

4 结束语

针对传统KH算法全局搜索能力弱，算法后期易陷入局部最优解，收敛速度慢等问题，通过引入自适应莱维飞行策略和HOT技术对算法寻优过程进行改进。通过该改进方法对ANFIS软测量模型反馈网络参数进行优化，减少ANFIS网络反馈过程的计算量，将该软测量模型应用于海洋溶菌酶发酵过程的菌体浓度预测中，通过仿真分析证明该方法对海洋溶菌酶发酵过程中菌体浓度预测控制具有很好的自适应和鲁棒性，具有良好的建模能力，可以应用于一般发酵工艺的物化参数和生物指标测量[27-28]。