具有可变延时的四元数神经网络的指数稳定性
2021-01-07徐晓惠杨继斌
徐晓惠,杨继斌
(西华大学汽车测控与安全四川省重点实验室,四川 成都 610039)
神经网络在联想记忆、优化问题求解、图像处理等多个领域得到了越来越多的应用[1-3],因此受到学者们的广泛关注。按照信号的性质不同,神经网络可分为实值神经网络(Real-valued neural networks)、复值神经网络(Complex-valued neural networks)及四元数神经网络(Quaternion-valued neural networks)。对于特殊场合的应用,比如彩色图像处理、阵列信号处理、风速预报等,实值神经网络和复值神经网络已经不能满足需求,而四元数作为复数理论在某种意义上的扩展在这些方面具有极大的优势[4]。由于乘法的不可交换性,四元数神经网络的性质比实值神经网络和复值神经网络更为复杂,而平衡点稳定性的研究是神经网络应用的前提条件;因此,四元数神经网络的动态行为的研究引起了学者们的关注。文献[5]研究了一类具有参数不确定性和脉冲干扰的四元数神经网络的动态行为,并得到了确保系统鲁棒稳定性的充分条件,然而在模型中没有考虑神经元之间信号传输的延时问题。文献[6 -7]在四元数神经网络模型中引入了固定延时。考虑到系统神经元个数较多,且不同神经元之间的信号传输所需要的时间不断变化;因此,文献[8 -10]在不同类型的四元数神经网络模型中引入了可变时滞。在研究四元数神经网络的动态行为时有3 种主流的研究方法,分别为LMI 方法[9-12]、加权Lyaounov 函数方法[7,13-14]和Cauchy 收敛原理[15]。学者们[7,9,11-15]得到了判定系统稳定性的充分条件。文献[7,9,11 -15]的稳定性条件中均含有自由变量,在实际应用时对自由变量的选择很大程度上依赖于人们的经验,选择不当会导致其他参数选择范围变小,进而使得设计的系统较为保守。此外,矢量Lyapunov 函数法在分析神经网络的动态行为时具有一定的优势,如函数构造形式简单、稳定性条件较为紧凑、无自由变量等。目前还没有学者采用矢量Lyapunov 函数法对四元数神经网络的稳定性进行研究。
基于以上分析,本文将在一类四元数神经网络模型中考虑可变时滞后,利用矢量Lyapunov 函数法和M 矩阵相关性质,研究该系统在平衡点的全局指数稳定性,并得到保守性较低且形式紧凑的稳定性判据。
1 预备知识和模型描述
首先给出一些符号定义。令 R,C和 Q分别表示实数域,复数域和四元数域。
对于一个四元数z=z(0)+z(1)i+z(2)ι+z(3)κ ∈Q(z(q)∈R,q=0,1,2,3)。Re(z)=z(0)表示z的实部,Im(z)=z(1)i+z(2)ι+z(3)κ表示z的虚部,其中i,ι和κ分别代表虚数单位。
首先给出四元数的Hamilton’s 规则[15]:

对于两个四元数,即z=z(0)+z(1)i+z(2)ι+z(3)κ ∈Q和y=y(0)+y(1)i+y(2)ι+y(3)κ ∈Q,加法和乘法运算规则分别如下:

本文考虑如下模型:
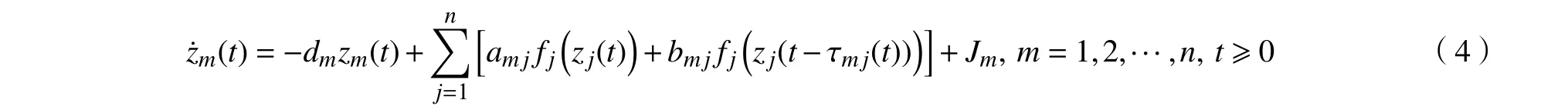
在系统(4)中,z(t)=(z1(t),z2(t),···,zn(t))T∈Qn代表神经元状态向量,D=diag(d1,d2,···,dn)∈Rn×n表示自反馈连接矩阵,其中dm>0,m=1,2,···,n。f(z(t))=(f1(z1(t)),f2(z2(t)),···,fn(zn(t)))T∈Qn代表神经元激活函数。A=(amj)n×n∈Qn×n和B=(bm j)n×n∈Qn×n为神经元之间的连接矩阵。J=(J1,J2,···,Jn)T∈Qn为外部输入向量。τmj(t)表示神经元之间的传输延时,τmj(t)是有界函数且满足τM=maxm,j∈{1,2,···,n}supt≥t0τmj(t)>0(m,j=1,2,···,n)。
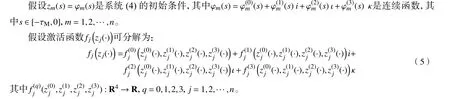
假设1激活函数fj(zj(·))满足fj(0)=0。对于任意给定zj,yj∈Q,存在常数>0 (q,qˆ=0,1,2,3,j=1,2,···,n)使得:

定义1若对于所有的J∈Qn和t≥t0,存在常数Γ >0和λ >0使得不等式Γexp(-λ(t-t0))成立,则平衡点~z是全局指数稳定的。
下面将系统(4)分解为1 个实部系统和3 个虚部系统:


其中:

2 稳定性条件



此时初始条件形式变为ψm(s)=φm(s)-(m=1,2,···,n)。显然系统(12)—(15)的原点是指数稳定的,则系统(11)的平衡点为指数稳定的。

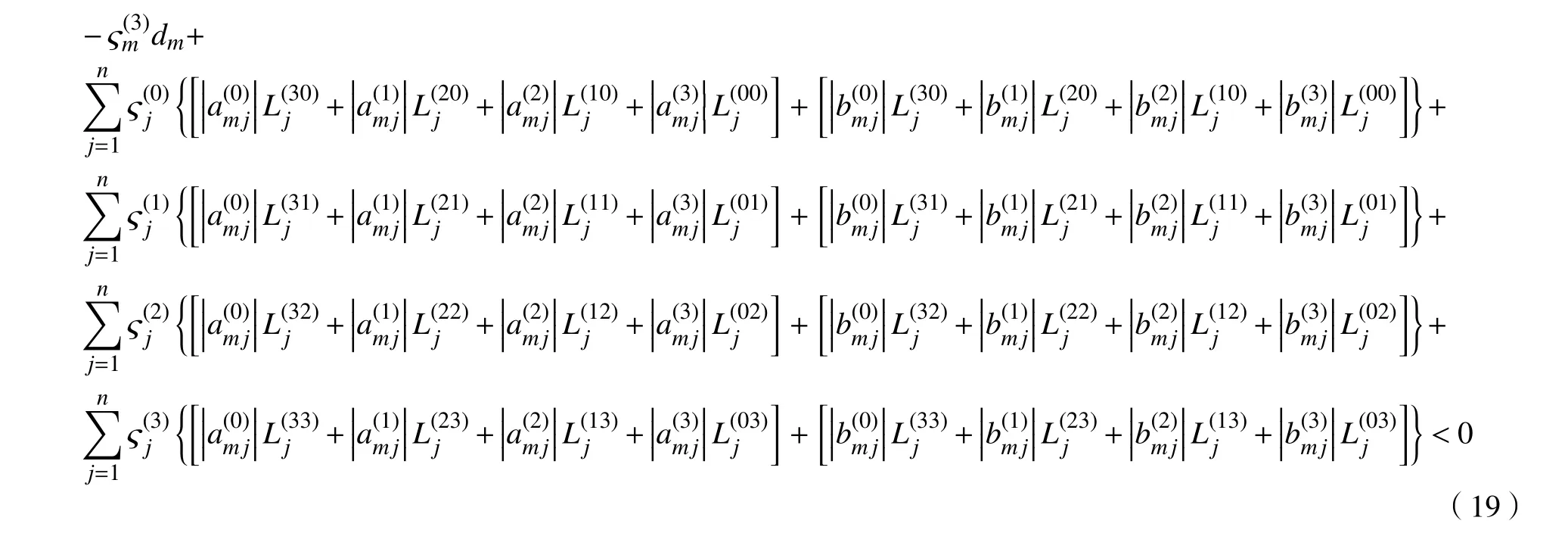
下面定义与系统(12)—(15)相关的4 个函数:
计算Vk(t,(t))k=1,2,···,n沿(13)的右上导数,并考虑到假设1,对所有,计算有:




注1:由式(5)可知:模型(4)中的激活函数在进行分解时满足强耦合条件,而文献[5,8 -9,11,16]中的激活函数满足弱耦合条件,选择激活函数时受到限制;因此,本文的假设条件更具有一般性。
注2:基于矢量Lyapunov 函数法和M 矩阵理论,定理1 以矩阵的形式给出了确保系统(4)指数稳定的充分条件。该判定矩阵中只包含系统自反馈系数、关联矩阵和激活函数,不含有任何待定条件或自由变量,相对文献[7,9,11 -15]中的稳定性条件,是一种较为直接的判据。此外,该判据形式紧凑且计算容易,在实际应用时更为方便和直观。
3 数值仿真
考虑如下系统:

注3:文献[15]也给出了判定系统(27)的解指数稳定的充分条件。将系统(27)的假设条件代入到文献[16]的推论4 中的稳定性条件,其他参数同文献[15]中的算例,计算结果如下:

图1 系统(27)的状态曲线

由上面计算结果可知,文献[15]推论4 中的稳定性条件显然是不成立的,因此根据推论4 无法判断出系统(27)的稳定性。然而,根据仿真结果(见图1)可以看出系统(27)的状态曲线是收敛的,同时本文定理1 也判断出了系统(27)的稳定性结论。因此,本文的稳定性条件给出的参数范围更广,具有更低的保守性。
4 结论
本文建立了一类具有可变时滞的四元数神经网络的数学模型,在假定激活函数满足强耦合条件的情况下,利用M 矩阵理论和矢量Lyapunov 函数法分析了该系统平衡点的全局指数稳定性,并给出了相关的稳定性判据。本文稳定性条件不仅形式简单易于应用,并且具有较大的参数范围。最后,本文通过给出的数值仿真算例验证了所得结论的正确性和低保守性。
