基于迭代稀疏组套索及SVM的高维分类研究

潘雪航

摘 要：高维数据存在大量的冗余变量和噪声，传统的分类方法在高维情况下通常效果不佳。为提高分类性能，将迭代稀疏组套索和支持向量机结合，提出了一种新的高维分类方法iSGL-SVM。分别在prostate和Tox_171数据集上验证了所提出的方法，并与其它三种方法进行比较。实验结果表明，该方法具有更好的变量选择效果和较高的分类精度，可广泛应用于高维小样本数据集的分类。

关键词：迭代稀疏组套索;支持向量机;高维分类;变量选择

中图分类号：O212      文献标识码：A

Abstract：There are a lot of redundant variables and noise in high-dimensional data， and traditional classification methods usually do not work well in high-dimensional situations. In order to improve the classification performance， the iterative sparse group lasso is combined with support vector machine， and a new high-dimensional classification method iSGL-SVM is proposed. The proposed method was verified on the prostate and Tox_171 datasets respectivelyand compared with the other three methods. The experimental results showed that the method has better variable selection effects and higher classification accuracy， which can be widely used for classification of high-dimensional small sample datasets.

Key words：iterative sparse group lasso; support vector machine; high-dimensional classification; variable selection

近年来，机器学习、生物信息学等各领域都出现了高维数据，并且已經很大程度上超过了以往的规模。如何从高维数据中提取重要信息，获得特征子集来进行数据分析一直是学者们面临的挑战。

通常情况下，高维数据包含成千上万个变量和少量样本，即p>>n，同时存在大量的冗余变量和噪声。在进行分类时，分类模型的性能依赖于选择合适的特征变量，同时去除不相关的特征变量。通过剔除冗余变量，能够带来更低的过拟合风险，更少模型的复杂性（因此提高了泛化能力）以及更低的计算成本[1]。因此，从高维小样本数据中去除冗余变量和选择相关变量可以提高分类模型的学习效率和分类准确率，从而有效地预测和制定政策。通常，在数万个变量中，只有一小部分变量起到关键性作用。换句话说，大多数变量与数据分类无关，这产生了噪声和降低了分类准确性。从机器学习的角度来看，变量太多总是会导致过拟合，对分类产生负面影响。因此，具有高预测精度的变量选择方法对于有效的高维数据分类是理想的[2]。

在科学研究中，分类模型已成为人工智能各个领域的有用工具，例如金融信用风险评估[3]，信号处理和模式识别[4]。为了避免维数灾难，从高维、海量的高维数据中选择有效的特征变量是分类的关键[5]。近年来，越来越多的学者热衷于使用稀疏方法作为分类的特征变量选择方法，因为它不仅能有效地解决维数灾难问题，而且能消除冗余变量和噪声，显著提高分类效果[6-8]。

Liu等人[9]提出了一种数据自适应核惩罚SVM 方法，这是一种同时实现特征选择和分类的新方法，特别是在数据不平衡的情况下;Li等[10]提出了一个用于精神分裂症疾病分类的深度经典相关稀疏自动编码器模型，并将提出的稀疏自动编码器模型应用于SNP数据和功能磁共振成像数据以检验其性能;Mohammed等人[11]使用了空间结构化的spike-and-slab先验，开发了一种贝叶斯方法来对多主体高维脑电图数据进行分类。Huo等[12]将Sparse Group Lasso与支持向量机结合，提出了一种新的高维分类SGL-SVM方法。

本研究的创新点在于改进了Huo提出的SGL-SVM分类方法，将SGL方法替换成iSGL[13]，提出了一种新的高维数据分类方法iSGL-SVM。该方法的优势是在变量选择部分，能够自动选择所有正则化参数，选择的特征变量更加准确可靠，提高了变量选择效果。

1 iSGL-SVM分类方法

传统的分类方法，如Fisher判别、逻辑回归等，在低维的情况下，即样本量大于变量个数时，能够很好地将不同标签的样本分类，分类效果较好。但是，当出现高维情况时，由于存在大量的冗余变量和噪声，如果使用传统的分类方法进行分类，分类效果会大大下降。所以需要使用高效的变量选择方法选择特征变量，然后使用分类器进行分类。

通常情况下，高维数据以分组形式出现[14]，例如单核苷酸多态性（SNP）和功能性磁共振成像数据（fMRI）。一个来解释预测变量群体结构的常用方法是Group Lasso（简称GL）。但这种方法只能实现组间稀疏，无法实现组内稀疏，因此往往会选择过多冗余变量。

2 实证分析

2.1 数据来源

实证分析使用两个数据集，一个二类prostate数据集和一个四类Tox_171数据集。Prostate数据集来源Singh等人[16]的研究。包含102例样本数据，其中正常人50例，患者52例，每个样本包含12600个变量，样本标签分别记为0和1。TOX_171数据集来源Stienstra等人[17]的研究。包含171例样本数据，每个样本包含5748个变量，样本标签分别记为1、2、3和4。

两个数据集具有以下特点： （1）所有实验数据均为真实的高维小样本数据;（2）变量数量远大于样本数量，即p>>n。（3）這些数据集包含大量冗余和不相关的变量。

2.2 评价指标

模型评价使用包括ACC、AUC、Kappa、召回率和F1评分等在内的评价指标。分类精度ACC定义如下：

根据表1，两个数据集的结果同时表明，使用RBF核函数时，分类性能最好。因此，在之后的实验中，支持向量机选择RBF核函数进行分类。

在两个数据集上，首先对归一化后的数据集采用Kruskal-Wallis秩和检验。KW检验能够检验多个总体分布是否存在显著差异，依次对不同总体的第i个变量进行KW检验。这个步骤能够除去数据集中大量的冗余变量，便于后续的变量选择。

然后，对处理后的数据集使用现有的iSGL-SVM方法进行分类，同时与EN-SVM、GL-SVM和SGL-SVM方法进行对比，选择RBF径向基核函数的支持向量机作为分类算法。

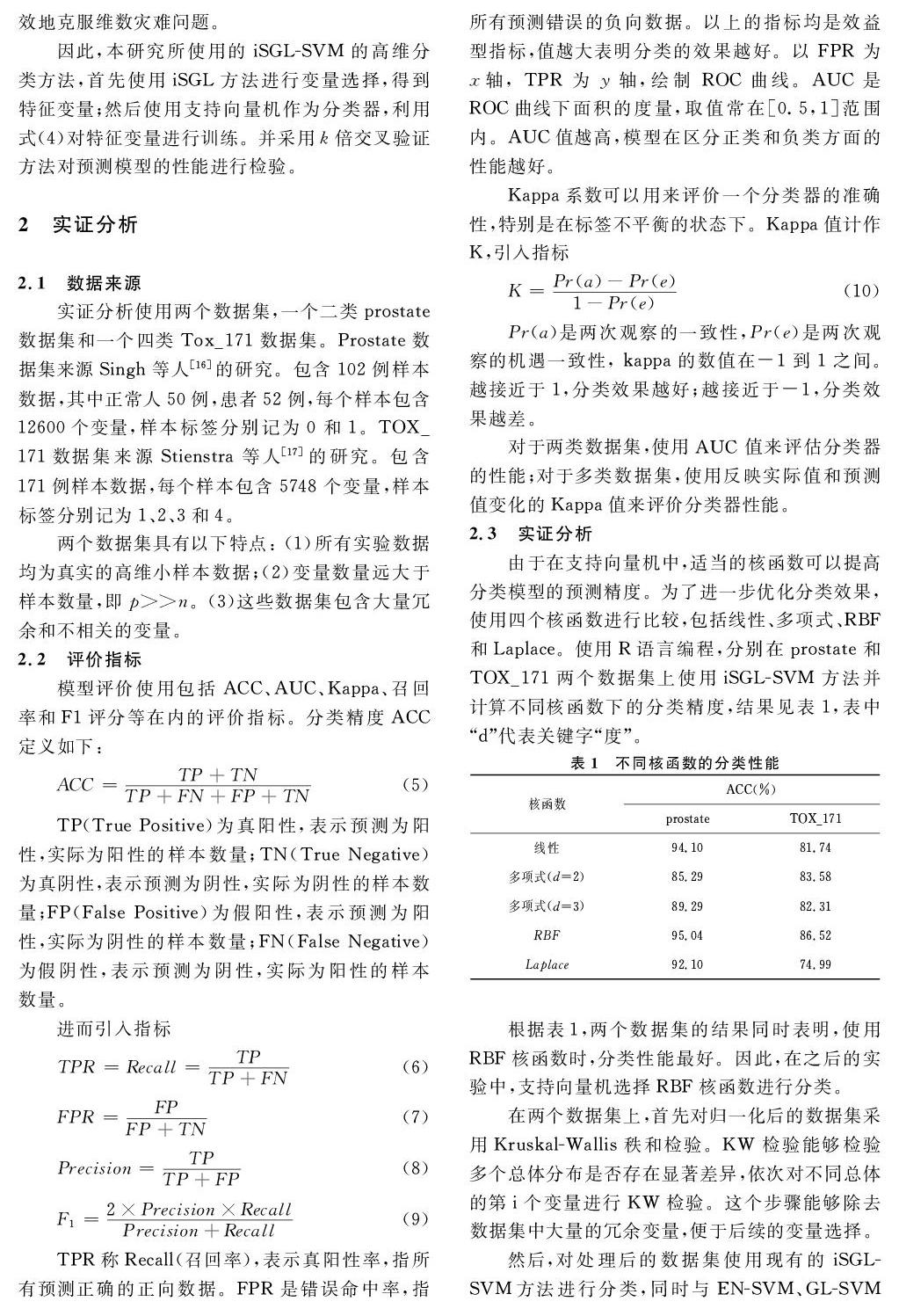
对于prostate数据集，使用5倍交叉验证对数据集进行测试和预测。对于TOX_171数据集，使用10倍交叉验证进行训练。使用R语言编程，计算出ACC等分类指标，比较两个数据集上四种不同算法对分类的影响。对于不同方法的平均精确率ACC值见表2。

根据表2，prostate数据集上，iSGL-SVM的分类精度达到了95%，而其他三种方法都在92%左右。由于该数据集只有两类，iSGL-SVM和其余三种方法的差别较小，优势并不明显;TOX_171数据集上，iSGL-SVM的分类精度达到了86%，EN-SVM的精度在83%左右，其余两种方法的准确度都低于80%，说明iSGL-SVM在多类数据集上分类效果更好，更具有优势。

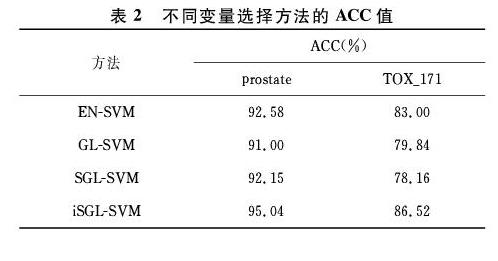
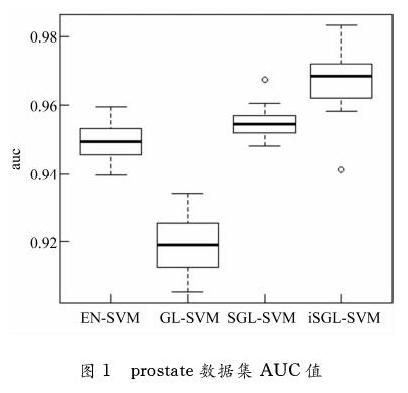
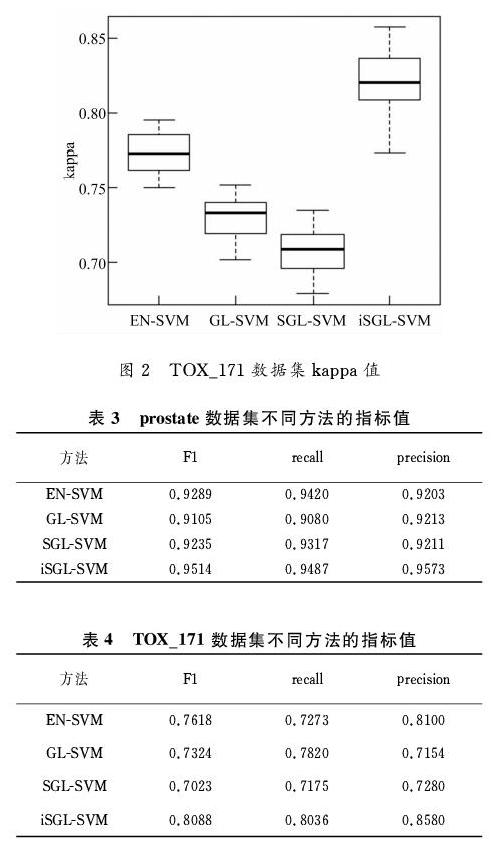
同时，分别对prostate数据集上进行的20次5倍交叉验证和TOX_171数据集上进行的20次10倍交叉验证计算了AUC、precision（阳性预测值）、F1评分和recall（召回率）四个评价指标。取AUC和Kappa值20次实验的均值作了箱线图，见图1和图2。20次实验的F1评分、recall和precision指标均值见表3和表4。

由图1和图2，iSGL-SVM方法在prostate数据集的AUC均值为0.9665，在TOX_171数据集的Kappa均值为0.8196，均高于其他分类方法，说明iSGL-SVM选择的特征变量更加准确可靠，获得了更高的分类效果。同时，由表3和表4，iSGL-SVM很好地获得了阳性预测值和召回率之间的权衡，而且从最高的F1评分（召回率和阳性预测值的加权调和平均）可以知道iSGL-SVM分类方法在高维数据分类上优于其他分类方法。这表明iSGL-SVM分类方法改善了高维数据的分类和预测。

3 结 论

将迭代稀疏组套索与支持向量机结合，提出了一种新的高维分类方法iSGL-SVM。实验结果表明，所提出的iSGL-SVM 方法在高维小样本数据中的分类表现优于其他三个相关方法。选择的变量更可靠，准确率更高。因此，所提出的方法在数据分类和预测方面显示出很大的前景，可广泛应用于高维小样本数据集的分类。

本研究只选择了支持向量机这一类分类方法，为此，可研究不同分类方法的影响，从而提高原方法的变量选择效果及预测效果。

参考文献

[1]BLUM A L， LANGLEY P. Selection of relevant features and examples in machine learning[J]. Artificial Intelligence， 1997， 97（1-2）： 245-271.

[2]WANG Y， LI X， RUIZ R. Weighted general group lasso for gene selection in cancer classification[J]. IEEE Transactions on Cybernetics， 2018， 49（8）： 2860-2873.

[3]ZHANG L， HU H， ZHANG D. A credit risk assessment model based on SVM for small and medium enterprises in supply chain finance[J]. Financial Innovation， 2015， 1（1）： 14.

[4]KHOKHAR S， ZIN A A B M， MOKHTAR A S B， et al. A comprehensive overview on signal processing and artificial intelligence techniques applications in classification of power quality disturbances[J]. Renewable and Sustainable Energy Reviews， 2015， 51： 1650-1663.

[5]BHARAT S. A meta-heuristic regression-based feature selection for predictive analytics[J]. Data Science Journal， 2014， 13： 106-118.

[6]BORGI M A， LABATE D， EL ARBI M， et al. Sparse multi-stage regularized feature learning for robust face recognition[J]. Expert Systems with Applications， 2015， 42（1）： 269-279.

[7]ALGAMAL Z Y， LEE M H. Penalized logistic regression with the adaptive LASSO for gene selection in high-dimensional cancer classification[J]. Expert Systems with Applications， 2015， 42（23）： 9326-9332.

[8]GAO J， KWAN P W， SHI D. Sparse kernel learning with LASSO and bayesian inference algorithm[J]. Neural Networks， 2010， 23（2）： 257-264.

[9]LIU X， ZHAO B， HE W. Simultaneous feature selection and classification for data-adaptive kernel-penalized SVM[J]. Mathematics， 2020， 8（10）： 1846.

[10]LI G， HAN D， WANG C， et al. Application of deep canonically correlated sparse autoencoder for the classification of schizophrenia [J]. Computer Methods and Programs in Biomedicine， 2020， 183： 105073.

[11]MOHAMMED S， DEY D K，ZHANG Y. Classification of high-dimensional electroencephalography data with location selection using structured spike-and-slab prior[J]. Statistical Analysis and Data Mining： The ASA Data Science Journal， 2020， 13（5）： 465-481.

[12]HUO Y， XIN L， KANG C， et al. SGL-SVM： A novel method for tumor classification via support vector machine with sparse group Lasso [J]. Journal of Theoretical Biology， 2020，486： 110098.

[13]LARIA J C， CARMEN A M， LILLO R E. An iterative sparse-group Lasso [J]. Journal of Computational and Graphical Statistics， 2019， 28（3）： 722-731.

[14]GOSSMANN A， CAO S， BRZYSKI D， et al. A sparse regression method for group-wise feature selection with false discovery rate control [J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics， 2018， 15（4）： 1066-1078.

[15]SIMON N， FRIEDMAN J， HASTIE T， et al. A sparse-group Lasso [J]. Journal of Computational and Graphical Statistics， 2013， 22（2）： 231-245.

[16]SINGH D， FEBBO P G， ROSS K N， et al. Gene expression correlates of clinical prostate cancer behavior [J]. Cancer Cell， 2002， 1（2）： 203-209.

[17]STIENSTRA R， SAUDALE F， DUVAL C， et al. Kupffer cells promote hepatic steatosis via interleukin-1beta-dependent suppression of peroxisome proliferator-activated receptor alpha activity [J]. Hepatology， 2010， 51（2）： 511-522.