基于Bézier曲线的碰撞角约束多项式制导方法

成忠涛 李聚峰 彭高祥 刘磊 王永骥

摘 要：研究了一种基于Bézier曲线的碰撞角约束的制导律。通过模型转化将制导指令设计的问题转化为二次Bézier曲线形式的航迹角设计问题。首先，利用Bézier曲线的性质设计了导弹速度大小不变的制导律;然后进一步对导弹速度时变的末端角度约束的制导律进行了研究，同时对导弹速度时变情形下的剩余飞行时间进行了估计;最后通过不同情况下的数值仿真，验证了所提出的制导律的有效性。

关键词：Bézier曲线;航迹角;碰撞角;制导律;剩余飞行时间

中图分类号：TJ765.3      文献标识码：A

飞行器制导律的设计一直是近几十年来研究的热点话题。随着导弹任务的多样化和作战场景的复杂化，对制导律提出了新的要求，如视场约束、碰撞时间控制和碰撞角控制[1-3]。其中，特定的碰撞角具有重要意义，第一，碰撞角控制制导律（IACG）可以引导导弹到达目标的最薄弱点;第二，特定任务的特定碰撞角度可以使杀伤能力最大化;最后，IACG可以引导导弹绕过防御系统。

IACG的最早研究可以追溯到1973年，Kim将其应用于再入飞行器[4]。他通过应用最优控制理论解决了碰撞角控制问题。Ryoo等针对不同的导弹动力学特性，提出了一种状态反馈形式的广义最优制导律[5]。进一步在一种新的飞行时间估计方法的基础上，提出了一种新的等速导弹最优碰撞角控制制导律[6]。文献[7]提出了一种新的线性最优IACG，与传统的框架不同，线性化不是在初始视线角附近进行的，而是在标称圆轨迹附近进行的。

Lyapunov稳定性和滑模控制等非线性控制理论，也被应用到IACG的设计中。文献[8]在Lyapunov候选函数中增加了一个碰撞角误差项，使之以特定的角度击中目标。文献[9]提出了一种基于减小航向误差角的Lyapunov候选函数的新型制导律，采用一种两级IACG来全方位命中目标。然而，在理论上，对于基于Lyapunov的制导律，只有当时间接近无限时，状态才会收敛到零。因此，其他一些研究涉及有限时间收敛IACG。文献[10]从滑模控制理论出发，提出了一种保证视线角在有限时间内收敛的IACG。文献[11]提出了一种非奇异终端滑模控制（NTSMC）的有限时间内收敛IACG，所得到的制导律能够以期望碰撞角命中目标。文献[12]得到了另一种有限时间收敛的制导律，这种制导律是由传统的NTSMC和二阶滑模控制相结合得到的。

除上述方法外，还采用几何和多项式方法推导了IACG。文献[13]首次提出了多项式制导的方法。之后，文献[14]提出了一种具有碰撞角和加速度约束的增广多项式制导律，制导指令以多项式函数形式给出，系数对应于碰撞角和加速度的约束。为了控制撞击时间和碰撞角，文献[15]提出了作为射程的函数的制导指令。文献[16]最新研究了涉及几何和多项式方法的自适应制导律。

上述对IACG的研究大多是基于等速假设。事实上，导弹的速度会受到推力、空气阻力及任务的进展而发生变化。因此，本研究将在导弹变速的情况下解决碰撞角控制问题。首先，通过问题描述将制导指令设计问题转化为航迹角的设计问题。然后，利用二次Bézier曲线拟合航迹角。最后，通过控制点的不同选择来实现碰撞角的控制。本研究在提出匀速导弹制导律的基础上，进一步提出了变速导弹的制导律，并对其剩余飞行时间进行了估计。

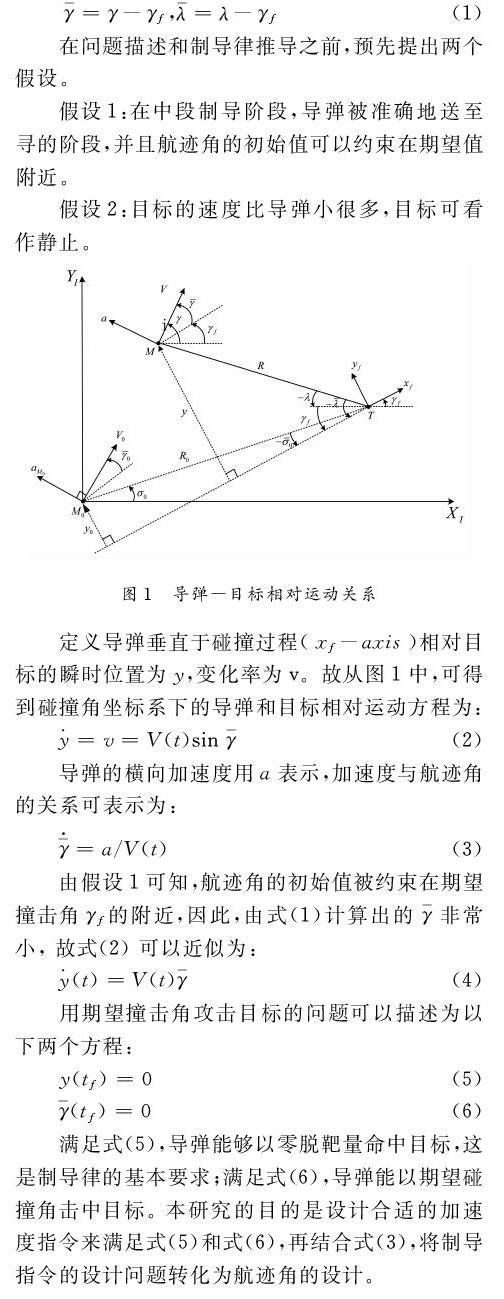
1 问题描述

3 数值仿真分析

本节中，将通过数值仿真来验证所提策略的有效性。在每种情况下，仿真步长均设为0.01 s。当相对速度符号变为正或相对作用距离小于0.01 m时，仿真终止。导弹的初始位置为（0，0），目标位置为（8000 m，0）。初始航迹角为30°。导弹初始速度为270 m/s，最大加速度为15 g，减速率为0.005。通过三个算例的仿真验证所提策略的有效性。

算例1 匀速导弹在相同初始条件下产生不同碰撞角

在此情况下，假设导弹的速度是恒定的，导弹期望碰撞角范围是-90°到0。从期望范围中选择四个典型的期望碰撞角。仿真结果如图2所示。

在图2中，实线和另外三种虚线分别代表不同的碰撞角。由图2d可知，所提出的制导律可以实现每个期望碰撞角。图2a为导弹轨迹，图2b为横向加速度，由图可知符合预定的加速度约束。图2c中，航向误差在终端时刻减小到零，保证了目标的脱靶量为零。仿真结果验证了所提制导律在匀速情况下是有效的。

算例2 匀速情况下不同的初始航迹角产生相同的碰撞角

该算例为证明在所提出的制导律下，不同的初始航迹角可以获得相同的碰撞角。给出三种不同的初始航迹角，分别为30°、60°和90°。仿真结果如图3所示。

在图3中，实线和另外两种虚线分别代表不同的航迹角。图3a为导弹轨迹，图3b为横向加速度，可以看出，当导弹的初始航迹角较大时，在初始时刻会产生较大的加速度指令。由图3c可知，所有航向角误差均减小到零。从图3d可知，导弹的初始航迹角不同，可以获得相同的期望碰撞角。因此，仿真结果验证了所提制导律在匀速情况下是有效的。

算例3 变速情况下的不同碰撞角问题

在此情况下，导弹速度不再被假定为常数。导弹的期望撞击角范围为-90°到90°。选择四个典型的期望碰撞角进行仿真，结果如图4所示。

在图4中，实线和另外三种虚线分别代表不同的碰撞角。由图4d可知，所提出的制导律可以实现每个期望碰撞角。图4b为横向加速度，由图可知其符合预定的加速度约束。由图4c可知，航向误差在终端时刻减小到零，保证了目标的脱靶量为零。因此，仿真结果验证了该制导律在变速度情况下是有效的。

4 结 论

提出了一种速度不变的碰撞角约束制导律，并进一步提出了速度时变的碰撞角约束制导律。该制导律是一条控制点待定的Bézier曲线形式的航迹角曲线。所提出的函数同时满足航迹角的初始条件和终止条件，并通过求解积分方程确定了未知系数，同时对提出速度时变制导律的剩余飞行时间進行了估计。通过不同的数值仿真，验证了所提出的制导律的有效性。在今后的工作中，制导律的设计还应考虑切向加速度的影响。

参考文献

[1] 赵曜，廖选平，迟学谦，等. 终端约束末制导律综述[J]. 航天控制，2017，35 （2）： 89-98.

[2] 黎克波，廖选平，梁彦刚. 基于纯比例导引的拦截碰撞角约束制导策略[J]. 航空学报，2020，41（S2）：79-88.

[3] 吴放，常思江. 攻击时间和攻击角度控制的非奇异终端滑模制导律[J].哈尔滨工业大学学报，2021，53（6）：94-103.

[4] KIM M，GRIDER K V. Terminal guidance for impact attitude angle constrained flight trajectories[J]. IEEE Transactions on Aerospace and Electronic Systems，1973，AES9 （6）： 852-859.

[5] RYOO C K，CHO H，TAHK M J. Optimal guidance laws with terminal impact angle constraint[J]. Journal of Guidance Control & Dynamics，2005，28 （4）：724-732.

[6] RYOO C K，CHO H，TAHK M J. Timetogo weighted optimal guidance with impact angle constraints[J]. IEEE Transactions on Control Systems Technology，2006，14 （3）：483-492.

[7] TSALIK R，SHIMA T. Optimal guidance around circular trajectories for impactangle interception[J]. Journal of Guidance Control & Dynamics，2016，39 （6）：1-14.

[8] KIM M，KIM Y. Lyapunovbased pursuit guidance law with impact angle constraint[C]. IFAC Proceedings Volumes，2014，47 （3）：2509-2514.

[9] CHENG Zhongtao，LIU Lei，WANG Yongji. Lyapunovbased switchedgain impact angle control guidance[J]. Chinese Journal of Aeronautics，2018，31（4）：765-775.

[10]ZHANG Yunxi，SUN Mingwei，CHEN Zengqiang. Finitetime convergent guidance law with impact angle constraint based on slidingmode control[J]. Nonlinear Dynamics，2012，70 （1）： 619-625.

[11]HOU Zhiwei，LIU Lei，WANG Yongji，et al. Terminal impact angle constraint guidance with dual sliding surfaces and modelfree target acceleration estimator[J]. IEEE Transactions on Control Systems Technology，2016，25（1）：85-100.

[12]HE Shaoming，LIN Defu，WANG Jiang. Continuous secondorder sliding mode based impact angle guidance law[J]. Aerospace Science & Technology，2015，41（2）：199-208.

[13]MIN B M，TAHK M J，SHIM H C D，et al. Guidance law for visionbased automatic landing of UAV[J]. International Journal of Aeronautical & Space Sciences，2007，8 （1）：4653.

[14]LEE C H，KIM T H，TAHK M J，et al. Polynomial guidance laws considering terminal impact angle and acceleration constraints[J]. Aerospace & Electronic Systems IEEE Transactions on，2013，49 （1）：7492.

[15]KIM T H，LEE C H，JEON I S，et al. Augmented polynomial guidance with impact time and angle constraints[J]. IEEE Transactions on Aerospace & Electronic Systems，2013，49 （4）：2806-2817.

[16]CHENG Zhongtao，WANG Bo，LIU Lei，et al. Adaptive polynomial guidance with impact angle constraint under varying velocity[J]. IEEE Access，2019，10（7）：104210-104217.

[17]馬帅，王旭刚，王中原，等. 带初始前置角和末端攻击角约束的偏置比例导引律设计以及剩余飞行时间估计[J]. 兵工学报，2019，40（1）：68-78.

[18]查世政，王永骥，苏茂.基于kriging滤波的高精度视线转率估计方法[J].计算技术与自动化，2014，33 （4）：20-25.