对一个运动斜面上摩擦力问题解法的探讨

郑 金

(凌源市职教中心 辽宁 朝阳 122500)

当斜面体在水平面上固定不动时，位于斜面上的物体在摩擦力的作用下可处于相对静止状态，而当斜面体沿水平方向加速运动时，位于斜面上的物体可能相对于斜面发生滑动或分离，这取决于斜面体运动加速度的大小和方向.但要注意刚好发生相对滑动的临界条件与刚好发生分离的临界条件是不同的，或者说，刚好相对滑动时不可能分离，而刚好分离时必将发生相对运动，刚好不分离的状态与刚好不滑动的状态完全不同，因此要注意这两种临界状态的区别，否则在解题时将会导致错误的结果.下面以《物理通报》2012年第3期第48面一道典型的动力学问题[1]为例进行分析.

【原题】如图1所示，劲度系数为κ的轻质弹簧一端与墙固定，另一端与倾角为θ的斜面体小车连接.小车置于光滑水平面上，在小车上叠放一个物体.已知小车质量为M，物体质量为m.当小车的左边缘位于O点时，整个系统处于平衡状态.现将小车从O点拉到B点，令OB=b，无初速释放后，小车在水平面的B和C两点间来回运动，物体和小车之间始终没有相对运动.求：b的大小必须满足什么条件，才能使小车和物体一起运动过程中，在某一位置时，物体和小车之间的摩擦力为零.

图1 题图

原解：当物体和小车之间的摩擦力为零时，取物体m为研究对象，有

mgtanθ=ma

取小车和物体组成的系统为研究对象，有

κb=(M+m)a

以上两式联立可得

为了使小车和物体在一起运动的过程中经过某一位置时二者之间的摩擦力为零，需小车在开始释放时到平衡位置的距离是一个范围，即

但b取值不能足够大，要想使物体和小车始终相对静止，b的最大值应是小车在B点时物体受到的支持力为零时取得，这时取物体为研究对象，有

取小车、物体和弹簧组成的系统为研究对象，有

κb=(M+m)a

以上两式联立可得

所以b的取值范围是

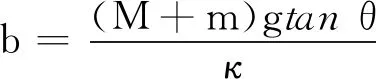
1 小车在平衡位置左侧与物体相对静止

当小车在平衡位置左侧刚释放时，加速度方向水平向右，可知当加速度较小时，物体有沿斜面向下滑的趋势；当加速度较大时，物体有沿斜面向上滑的趋势.物体刚好不滑动的临界条件是受到的摩擦力刚好达到最大静摩擦力，为了使小车在C点刚释放时物体与小车保持相对静止，初始加速度应存在一个取值范围，即在最小值和最大值之间，因此C点在弹簧振子的平衡位置左侧存在两个极端位置，则形变量b对应两个极值，下面分别推导加速度的最小值和最大值及其对应C点的位置.

其一，当小车刚释放时的加速度取最小值时，物体有沿斜面向下滑的趋势，则受到的摩擦力沿斜面向上，设此时静摩擦力刚好达到最大值，则在垂直于斜面方向由牛顿第二定律有

N-mgcosθ=masinθ

在平行于斜面方向由牛顿第二定律有

mgsinθ-μN=macosθ

联立方程可得小车刚释放时加速度的最小值为

与方程κb=(M+m)a联立可得

由题意可知在简谐运动的过程中物体与小车始终保持相对静止，那么当小车运动到平衡位置时，即加速度为零时，二者仍然保持相对静止，则动摩擦因数至少为μ=tanθ，即μ≥tanθ.而另一方面，由

可得

μ

这与μ≥tanθ发生矛盾，因此在μ>tanθ的条件下，amin不存在，即在小车向右加速运动的过程中不会出现物体刚好沿斜面下滑的情况.或者说，在简谐运动的过程中，如果物体与小车始终保持相对静止，那么当小车运动到平衡位置时，即加速度为零时物体不下滑，因此，在小车从平衡位置左侧向右加速运动或从平衡位置向左减速运动的过程中，即在超重状态下物体不可能沿斜面下滑，只需b>0即可.

其二，当小车刚释放时的加速度取最大值时，物体有沿斜面向上滑的趋势且刚好不滑动，那么受到最大静摩擦力的方向沿斜面向下.应用牛顿第二定律列方程，在平行于斜面方向有

mgsinθ+μN=macosθ

在垂直于斜面方向有

N-mgcosθ=masinθ

联立方程可得小车刚释放时加速度的最大值为

可知

综上可见，当小车位于平衡位置左侧时，为了使物体始终不发生相对滑动，b的取值范围应是0

下面推导物体受到的摩擦力刚好为零时的加速度的临界值及其对应C1点的位置.

在小车从平衡位置左侧向右运动的过程中，由于加速度逐渐减小，物体受到摩擦力的方向将发生改变，因此存在摩擦力为零的情况.当物体受到的摩擦力刚好为零时，在水平方向由牛顿第二定律有

mgtanθ=ma0

可得临界加速度为

a0=gtanθ

对于a0还有一种求解方法，当摩擦力刚好为零时，即使斜面光滑，物体也不发生滑动，那么把μ=0代入

可得

a0=gtanθ

由

κb=(M+m)a

可得

为了使物体与小车保持相对静止而且在某时刻受到的摩擦力为零，那么小车在平衡位置左侧刚释放时到平衡位置的距离应满足b0

(1)

2 小车在平衡位置右侧与物体相对静止

当小车在B点刚释放时将加速向左运动，物体在失重的状态下只有沿斜面向下滑的趋势，为了使物体与小车保持相对静止，物体受到摩擦力的方向必须沿斜面向上.这是因为整个弹簧振子受到的最大回复力方向水平向左，则最大加速度方向水平向左，那么物体受到的最大合力方向水平向左，由于重力竖直向下，支持力垂直于斜面向右，所以最大静摩擦力方向一定沿斜面向左.由于加速度越大，越容易发生相对滑动，因此小车刚释放时的加速度存在最大值，此时物体刚好不发生滑动，但有沿斜面下滑的趋势，摩擦力刚好为最大静摩擦力fm=μN.在垂直于斜面方向由牛顿第二定律有

mgcosθ-N=masinθ

在平行于斜面方向由牛顿第二定律有

fm-mgsinθ=macosθ

联立方程可得小车刚释放时的最大加速度为

对于a′max还有一种求解方法，对物体m在竖直方向由受力平衡有

fsinθ+Ncosθ=mg

在水平方向由牛顿第二定律有

fcosθ-Nsinθ=ma

当摩擦力为最大静摩擦力时，有f=μN.联立方程可得a′max.

对整体由牛顿第二定律有κb=(M+m)a，可得

如果向左的加速度过大，物体与小车将发生分离.当物体与小车刚要分离时，物体受到的支持力刚好为零，此时摩擦力也刚好为零，物体只受重力，做自由落体运动的加速度为ay=g，小车的加速度为ax=a.刚要分离时二者在垂直于斜面方向的加速度相等，即

gcosθ=asinθ

可得最大加速度

(2)

3 小车在简谐运动过程中与物体相对静止

设bmax对应小车的位置在C2点，b0对应小车的位置在C1点，b′max对应小车的位置在B点，可画出小车在平衡位置两侧时弹簧形变量b的临界值对应小车所在的位置分布如图2所示.

图2 弹簧形变量对应小车所在位置

观察bmax和b′max的表达式可知，一定有bmax>

(3)

这就是原题的正确答案，也可由不等式(1)和(2)取交集而得到.但对原题还需补充动摩擦因数为μ，否则在答案中将出现未知量.

即

μtan2θ+2tanθ-μ<0

可得

利用倍角公式得μ>tan 2θ.

为了在简谐运动过程中出现摩擦力为零的情况，应满足μ>tan 2θ，即tan 2θ<μ，则θ<0.5arctanμ，这是保证式(3)成立的前提条件.如果不满足这个条件，那么式(3)将不成立，就不会出现摩擦力刚好为零的状态.在一般情况下μ<1，则2θ<45°，即θ<22.5°，而不是θ<45°.由此可见，小车斜面的倾斜角应该是比较小的，这样才满足题意.在μ>tan 2θ的条件下，必定满足μ>tanθ，那么当小车运动到平衡位置时物体一定不下滑.所以原题的完整答案应为式(3)和约束条件μ>tan 2θ.