压杆稳定性的平衡视角与刚柔渐近

李 敏 李依伦(北京航空航天大学航空科学与工程学院，北京100191)

†(北京航空航天大学中法工程师学院，北京100191)

1 教学内容回顾与问题的提出

在材料力学课程体系中，作为结构安全性三大指标之一的稳定性是以压杆稳定性，特别是临界载荷的求解为主要教学内容。教学内容除稳定性现象描述外，还包括：刚杆与弹簧压杆稳定性分析；两端铰支细长压杆临界载荷的推导与讨论；两端非铰支细长压杆临界载荷的推导与比拟；中、小柔度压杆临界应力；压杆稳定条件与合理设计。

笔者在多年的教学实践中发现：在所有稳定性教学内容中，同学们在临界载荷公式应用方面掌握较好，但提及什么是压杆失稳以及为什么会失稳往往不能准确描述，这反映出学生在理解压杆稳定性的机理方面有欠缺。究其原因，一方面，相比强度与刚度分析中拉压、扭转、弯曲章节的重复强化，稳定性分析教学内容较少，所以学生感受不充分；另一方面，稳定性分析属于特征值问题，其分析方法与强度和刚度所归属的响应问题差异较大。以上的原因使学生们普遍对压杆稳定性章节产生一种“雾里看花”的感觉，因此找寻一种采用学生们熟知的分析模式，或者基于已有理论基础的教学方法非常必要。

事实上，除了弹性压杆稳定性的分析过程，刚杆-弹簧系统稳定性的分析，包括为了讲述方便而引入的刚性小球凹凸曲面稳定性问题(图1)，同学们认为稳定性的机理是比较清晰的：

(1)对于刚性小球--从力平衡的角度出发，当小球偏离平衡点A后，凹曲面内小球所受合力始终指向平衡位置；而凸曲面外小球所受合力始终背离平衡位置B，所以平衡点稳定性的机理一目了然；

(2)对于刚杆-弹簧轴向受压稳定性问题(图2)，基于从中学就熟悉的力(矩)平衡的知识，也能迅速领会驱动力矩Fδ与恢复力矩kδl的相互关系决定刚杆-弹簧系统直线平衡状态稳定性的机理，这与刚性小球平衡点稳定性分析一脉相承：均为力(矩)平衡关系的视角，而这种基于中学或大学物理课程中力(矩)平衡的分析模式很容易被学生们接受与掌握。

图1 刚性小球凹凸曲面平衡稳定性示意图

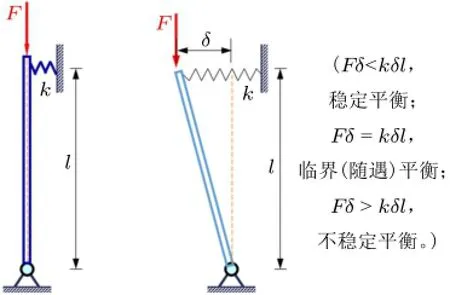
图2 刚杆-弹簧压杆平衡稳定性示意图

在两端铰支弹性细长压杆稳定性分析过程中，利用梁的挠曲轴(近似)微分方程，代入微弯临界状态下弯矩表达式，通过边界条件与通解存在条件确定临界载荷，在此过程中并未明显涉及熟知的力(矩)平衡，而是借用了常微分方程解算模式，致使解答(临界载荷)的物理含义不明晰。后续讲解临界载荷π2EI/l2属于结构的固有特性时，尽管学生们基于表达式的形式可以接受这一结论，但讲解中物理本质的缺失是学生理解弹性压杆稳定性机理的主要障碍。

2 弹性压杆稳定性问题的力(矩)平衡视角

事实上，在两端铰支弹性细长压杆分析过程中也有驱动力矩与恢复力矩的分类：在微弯临界状态下分离体平衡(图3)，由此获得内力分量的弯矩M与外力矩Fw平衡，其中弯矩M即为恢复力矩，而外力矩Fw为驱动力矩。尽管这种讲述方式也被部分教师采用，但相比刚杆-弹簧系统中恢复力矩kδl明确的物理含义，弹性压杆恢复力矩M与结构几何尺寸和材料有何关系并不明确，导致该种讲述方式失去阐述内在机理的价值。

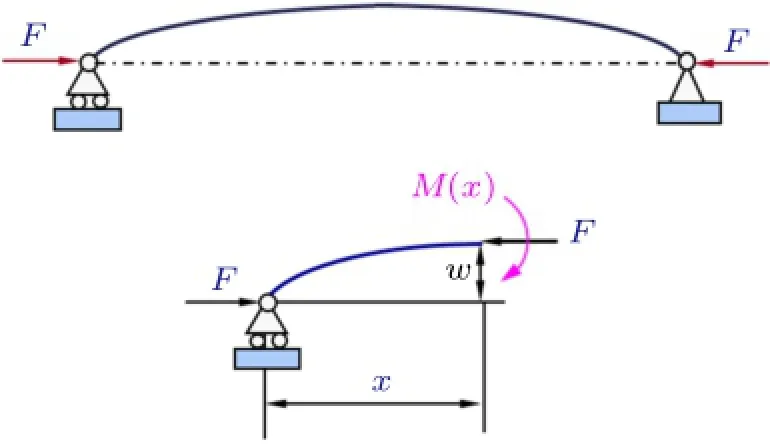
图3 弹性压杆平衡稳定性分析内力图

本文提出一种方法修补该缺陷，建议在基本内容讲述完成后对分析内容进行另一种模式的回顾：当弹性压杆处于微弯临界状态，利用挠曲轴近似微分方程与挠度解的形式，由

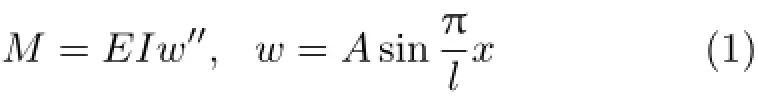
得

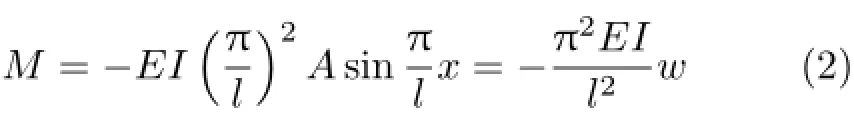
为了形象化表征各力矩变化与相互关系，使用图4表示弹性压杆系统的力矩变化，其中横轴表示外加轴向压力，纵轴表示力矩。当杆件偏离初始直线平衡位置时，图中OA1直线表示随着轴向压力F的增加，x=x1截面(任意轴向位置)驱动力矩Fw(x1)呈线性增长；而恢复力矩M=π2EIw(x1)/l2与外加轴向压力F无关所以呈水平直线(图中B1C1)(式(2)中负号表示恢复力矩M与驱动力矩方向相反，为了便于画图比较，图中只考虑数量)。两线相交点D1表征临界状态，其交点对应横坐标即为临界载荷Fcr=π2EI/l2。图中Fcr左侧箭头表示：当外加轴向压力F＜Fcr时，线段B1D1位于OD1之上，即恢复力矩大于驱动力矩，压杆将回到原始直线平衡位置；同理，右侧箭头表示外加轴向压力F＞Fcr时恢复力矩小于驱动力矩(线段D1C1位于D1A1之下)，压杆无法回到原始直线平衡位置。当然也可以取不同的轴向位置x=x2，情况是完全类似的：OA2表示驱动力矩Fw(x2)，B2C2表示恢复力矩π2EIw(x2)/l2，两线交点D2所对应的临界载荷仍为Fcr。

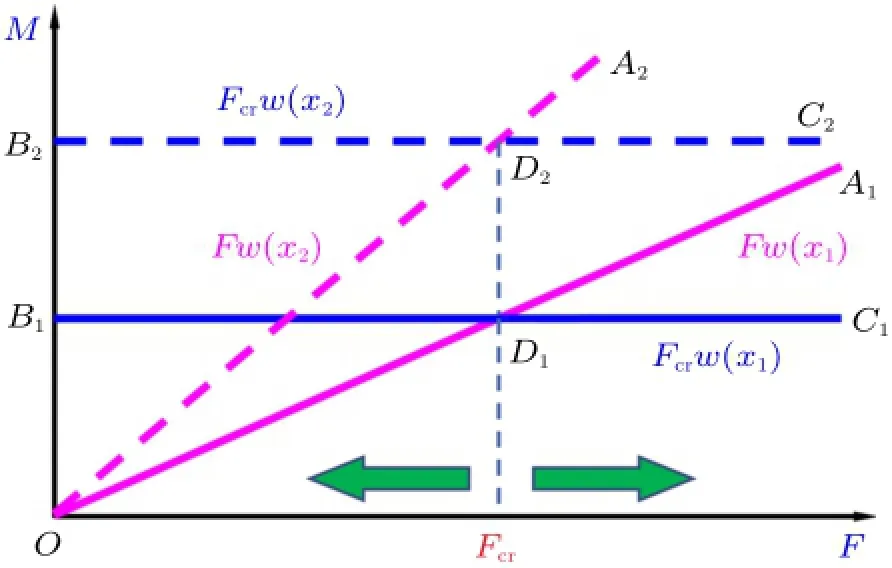
图4 弹性压杆系统的力矩变化

刚杆-弹簧系统驱动力矩Fδ与恢复力矩kδl的相互关系完全类似(如图5，图中δi均表示压杆上端部水平位移)，此处不再赘述。

图5 刚杆-弹簧系统的力矩变化

沿袭力(矩)平衡的视角，采用该类图线可以展示驱动力矩与恢复力矩的关系，临界载荷的来历，以及外力小于或大于临界载荷时系统的状态，不失为一种帮助学生理解弹性压杆稳定性机理的方法。

以上的分析模式从形式上统一了刚杆-弹簧系统与弹性压杆系统失稳机理，但相比于刚杆-弹簧系统恢复力矩的来源，弹性压杆系统的恢复力矩源于挠曲轴近似微分方程与挠度解的形式，也许会使学生感觉有些“陌生”或者“不直接”。更重要的是，相比前者临界载荷kl作为系统固有特性的物理本质，后者临界载荷π2EI/l2不易理解：尽管从直观感受上，结构抵抗失稳的能力与刚度成正向比例，与杆长度成反向比例是合理的，但比例的方次，包括系数大小，以及π2EI/l2从总体形式上与结构的什么性质直接关联并不明显。讲述内容中刚杆-弹簧系统与弹性压杆系统两种稳定性问题还是相对独立的，这是以上方法的“缺憾”。

3 压杆稳定性问题的刚柔渐近

为了解决上节方法中的“缺憾”，这里首先介绍一个典型题目(图6)，该题目出现在许多教科书中作为例题或习题[1-3]。

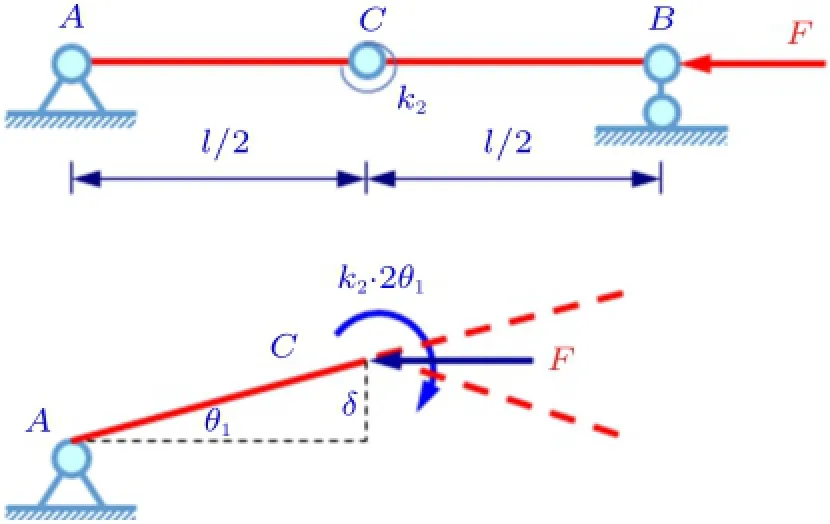
图6 双刚杆+线性碟簧系统稳定性问题示意图

双刚杆+一个线性碟簧(螺旋弹簧)系统临界载荷的解算是非常简单的，考虑微扰临界状态下分离体刚杆AC的平衡

则

在双杆模型的基础上进行扩展，使用相同的方法可以解算多杆+线性碟簧模型的临界载荷，对于三杆模型(图7)，根据对称性，CD杆处于水平位置，其力平衡分析与双杆模型相同

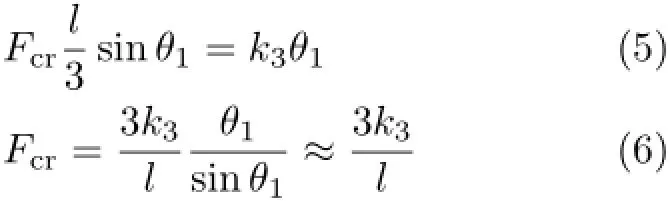
四杆模型(图8)需考虑AC杆与CD杆的平衡

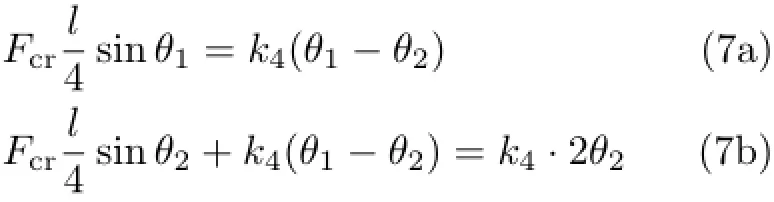
联立可得θ1与θ2的关系

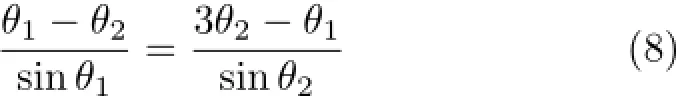
可解得θ2/θ1=■2-1，即

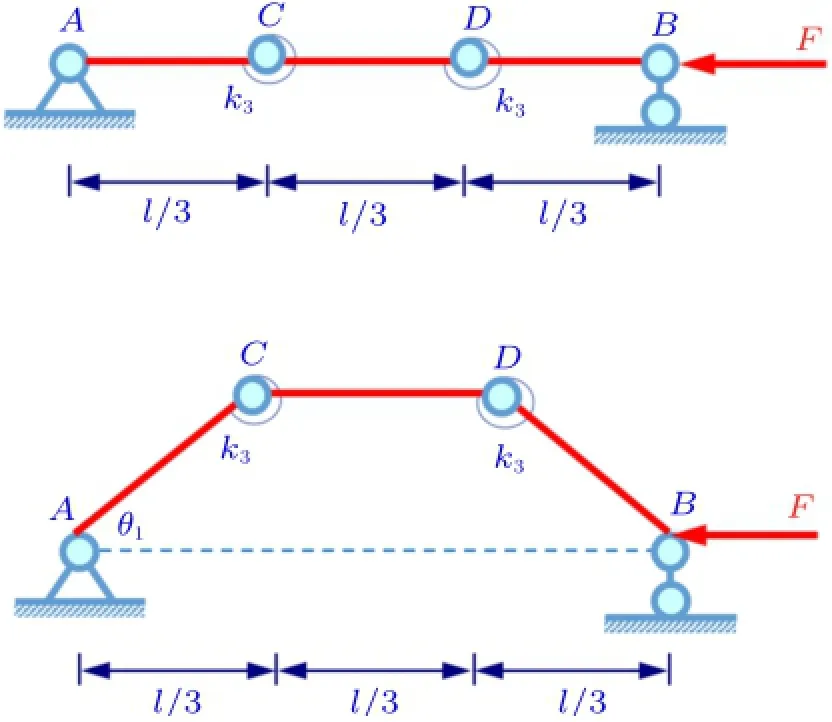
图7 三刚杆+线性碟簧系统稳定性问题示意图

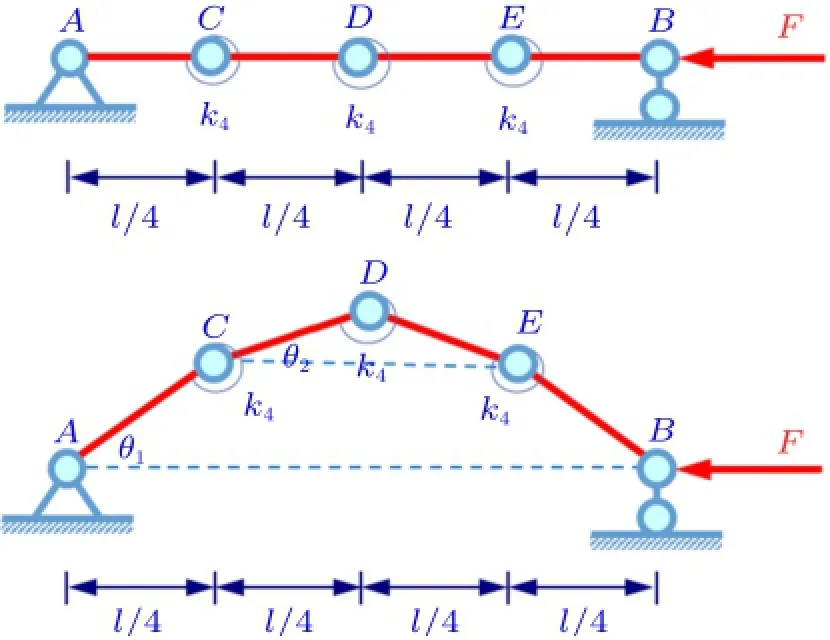
图8 四刚杆+线性碟簧系统稳定性问题示意图

更多杆件模型均可参照以上的平衡条件解出，另外也可利用最小势能原理，采用变分方法进行简化分析，以下给出各模型的势能表达式

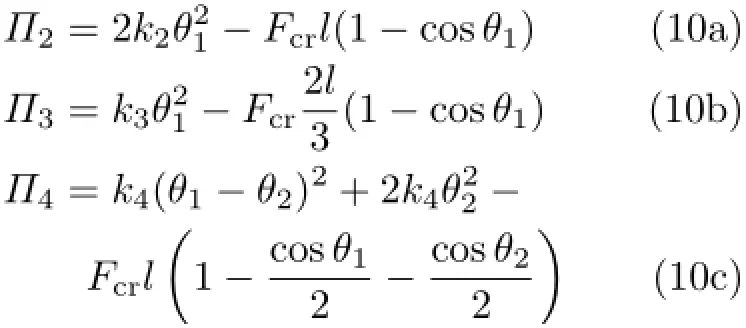
式中，Π的下标表示杆件数目，对θi变分即可得到平衡方程，这里不再详述[4]。

观察式(4)，式(6)和式(9)等系列结果并顺序排列，从形式上完全相似，临界载荷均与线性碟簧刚度成正比，与刚杆长度成反比。考虑到图中蝶形弹簧刚度的物理含义是相邻两刚杆产生单位转角所需力矩，如果关联到弹性梁弯曲变形中集中弯矩产生的弯曲角

可得

式中li=l/i。代入各模型临界载荷公式中整理成为统一的模式

式中ai数值如表1。

表1 ai数值表

随着杆件数目的增加，依据式(12)我们可以猜测ai的发展趋势是否有可能趋近π2≈9.87。

事实上，我们可以证明这一点：对于总长l等分i段(i→∞)的刚杆+线性碟簧模型如图9，考虑对称性取左半部分为研究对象(为方便画图，不妨设i为偶数)，

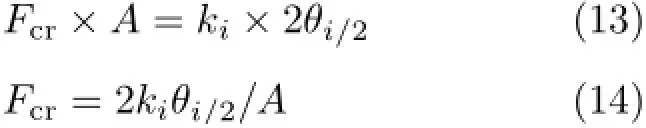
沿用形状函数Asinπx/l，极限状态下中点附近弯曲角极小，利用小变形假设

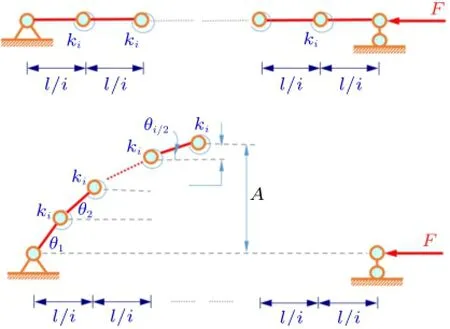
图9 无限细分刚杆+线性碟簧系统稳定性问题示意图

对于压杆稳定性教学内容的讲解，特别是压杆稳定性内涵的理解，此例有两方面的作用：

(1)说明了弹性压杆稳定性临界载荷π2EI/l2中各参数与方次的来历。

(2)统一了刚杆-弹簧压杆稳定性与弹性压杆稳定性两种压杆稳定性模式，前者是后者在一定条件下的近似，后者可以看作前者的极限化。

4 结语

在材料力学课程内容中，弹性压杆稳定性临界载荷的物理本质属于比较难于理解的部分。相对而言，基于中学或者大学物理中有关力(矩)平衡的基础知识进行讲解容易被学生接受。本文通过几种简单模型和图像展示，揭示了弹性压杆稳定性临界载荷中各参量与杆件弯曲刚度和几何尺寸的关系，并统一了两种压杆稳定性模型的分析过程，可作为材料力学压杆稳定性部分教学的补充材料。