北风卷地白草折——漫话湍流边界层中的涡旋结构

杨绍琼 姜楠

(天津大学机械工程学院，天津300354)

白雪歌送武判官归京

岑参(唐)

北风卷地白草折，胡天八月即飞雪。

忽如一夜春风来，千树万树梨花开。

散入珠帘湿罗幕，狐裘不暖锦衾薄。

将军角弓不得控，都护铁衣冷难着。

瀚海阑干百丈冰，愁云惨淡万里凝。

中军置酒饮归客，胡琴琵琶与羌笛。

纷纷暮雪下辕门，风掣红旗冻不翻。

轮台东门送君去，去时雪满天山路。

山回路转不见君，雪上空留马行处。

《白雪歌送武判官归京》[1]是唐朝著名边塞诗人岑参(约715-770年，图1)的代表作。唐朝时期，西北边疆一带战事频繁，岑参怀着到塞外建功立业的志向，两度出塞，久佐戎幕，前后在西北边疆军队中生活了六年，因而对鞍马风尘的征战生活与冰天雪地的塞外风光有长期的观察与体会，他的大多数边塞诗成于这一时期。这些边塞诗歌是他对边塞风光，军旅生活及少数民族的文化风俗的亲身感受。唐玄宗天宝十三年夏秋之交，岑参第二次出塞，充任安西北庭节度使封常清(690-756年)的判官，也就是节度使的僚属，而武判官即其前任(中唐名相武元衡(758-815年)的父亲武就(731-790年)[2])。诗人在轮台送他归京而写下了此诗。

此诗描写西域八月飞雪的壮丽景色，抒写塞外送别、雪中送客之情，表现离愁和乡思，却充满奇思异想，并不令人感到伤感(图2)。诗中所表现出来的浪漫理想和壮逸情怀使人觉得塞外风雪变成了可玩味欣赏的对象。全诗内涵丰富宽广，色彩瑰丽浪漫，气势浑然磅礴，意境鲜明独特，具有极强的艺术感染力，堪称“盛世大唐边塞诗的压卷之作”。其中“忽如一夜春风来，千树万树梨花开”等诗句已成为千古传诵的佳句。

图1 唐朝著名边塞诗人岑参(约715-770年)

图2 美术作品《白雪歌送武判官归京》

岑参还有一首著名的边塞诗《走马川行奉送出师西征》[3](也称《走马川行奉送封大夫出师西征》)：

君不见走马川行雪海边，平沙莽莽黄入天。

轮台九月风夜吼，一川碎石大如斗，随风满地石乱走。

匈奴草黄马正肥，金山西见烟尘飞，汉家大将西出师。

将军金甲夜不脱，半夜军行戈相拨，风头如刀面如割。

马毛带雪汗气蒸，五花连钱旋作冰，幕中草檄砚水凝。

虏骑闻之应胆慑，料知短兵不敢接，车师西门伫献捷。

此诗作于公元754年(唐玄宗天宝十三年)。这期间，封常清曾几次出兵作战。这是岑参为封常清出兵西征而创作的送行诗。这首诗将西北边塞风沙的猛烈、人物的豪迈，描写的惟妙惟肖，给人以雄浑壮美之感。为了表现出边防将士高昂的爱国精神，诗人用了反衬手法，抓住有边地特征的景物来状写环境的艰险，极力渲染、夸张环境的恶劣来突出人物不畏艰险的精神。诗中运用了比喻、夸张等艺术手法，写得惊心动魄，绘声绘色，热情奔放，气势昂扬。

唐朝另一位大诗人杜甫(712-770年)也有一首著名的《茅屋为秋风所破歌》[4]描写北风：

八月秋高风怒号，卷我屋上三重茅。

茅飞渡江洒江郊，高者挂罥长林梢，下者飘转沉塘坳。

南村群童欺我老无力，忍能对面为盗贼。

公然抱茅入竹去，唇焦口燥呼不得，归来倚杖自叹息。

俄顷风定云墨色，秋天漠漠向昏黑。

布衾多年冷似铁，娇儿恶卧踏里裂。

床头屋漏无干处，雨脚如麻未断绝。

自经丧乱少睡眠，长夜沾湿何由彻！

安得广厦千万间，大庇天下寒士俱欢颜！

风雨不动安如山。呜呼！何时眼前突兀见此屋，吾庐独破受冻死亦足！

在这些诗歌里，都描写了一种自然现象，就是“风”。风的威力很大，可以“北风卷地白草折”，也可以“随风满地石乱走”，还可以“卷我屋上三重茅”。从文学的角度来看，这是诗人用了夸张反衬手法，通过气势磅礴的描写，极力渲染环境的恶劣，体现诗人的浪漫理想和壮逸情怀。而从流体力学的角度来看，这是诗人对自然现象细致入微的观察和理性的思考，是符合近代流体力学科学原理的。那么，为什么风的威力这么大呢？这还要从两个流体力学重要概念--“边界层”和“湍流”谈起。

1 流体的“边界层”

图3 著名流体力学家路德维希·普朗特的照片(作者2009年在德国哥廷根DLR空气动力与流动技术研究所翻拍)

图4 普朗特进行边界层实验的照片(作者2009年在德国哥廷根DLR空气动力与流动技术研究所翻拍)

流体绕流过固体时，在固体表面附近很薄的区域内形成流体的“边界层”。边界层这个概念是德国著名流体力学家路德维希·普朗特(Ludwig Prandtl，1875-1953，图3)于1904年提出来的。他用撒在水里很细的铝粉观察水槽里的水流动时(图4)，发现靠近水槽边壁的水流速度慢，远离水槽边壁的水流速度快。由此，他提出在靠近固体边壁的附近，流体的黏性起了很大的作用，流体的流向速度存在一个随着远离边壁逐渐增长的区域，这个区域是边壁附近一个很薄的流体层，称为边界层。流体和边壁的流向相对速度在边壁上为零，随着远离壁面，流体的流向相对速度逐渐增加，直到出了边界层，流体的流向速度不再变化。在边界层内，流体的运动必须考虑黏性的影响，在边界层外，可以不考虑流体的黏性对流动的影响。普朗特提出的边界层理论非常重要，他既考虑了流体的黏性在边壁附近的重要性，符合实际流动的规律，又可以在远离边壁的地方不考虑黏性的影响，使问题简化。在1904年德国海德尔堡(Heidelberg)第三次国际数学年会上他发表了4页纸的论文“¨Uber Fl¨ussigkeitsbewegung bei sehr kleiner Reibung(关于极小摩擦的流体运动)”[5]，正式提出著名的边界层概念，深刻阐述了绕流物体在大雷诺数情况下，表面受黏性影响的边界层流动特征及其控制方程，巧妙地解决了整体流动和局部流动的关系问题，从而为解决黏性流体绕过物体的阻力问题找到了新的途径，填补了经典的理论流体力学与经验的工程水力学之间的鸿沟，起到划时代的里程碑作用，因而被称为近代流体力学的开端，普朗特本人也被称为近代流体力学之父。

2 湍流

流体的流动状态分为“层流”和“湍流”两种。层流是流体有序的流动，流体所包含的动量、能量和物质的传输主要靠流体分子。但层流是不稳定的，很容易转变为湍流。湍流使得流动非常混乱，产生大大小小各种尺度、各种形状的涡旋结构，使得流体的动量、质量、能量的传递能力大幅提高。例如：在内燃机燃烧室内，就希望湍流的混乱程度越高越好，因为越高越有利于燃料和氧气的充分混合，燃烧得越充分，越能提高燃烧效率，节省燃料，减少有害物质的排放。在化工装备中，也希望湍流的混乱程度越高越好，这有利于物料的充分混合，加快反应速度，提高反应效率。但是，对于航空航天飞行器的外部流场，我们就不希望流动是湍流，因为湍流流动使得飞行变得不稳定，使飞行器的振颤抖动加剧，壁面摩擦阻力增大，能量消耗增加，特别是高速飞行器，湍流会使得其壁面热流增大，其有效载荷降低，使其变得更加不稳定和难以被控制。

最早观察湍流流动的应该是意大利文艺复兴时期的大科学家达·芬奇(1452-1519，图5)[6]。在爱德华·马克库蒂的《列奥纳多·达·芬奇笔记》[7]中，其关于一般水流和“湍涡”的详细描述就单独占用了121页。在这本笔记手稿中，达·芬奇最早提出了“湍涡”的概念并分析了其成因。他的手绘(图6)或许是现世最早的“湍流涡旋”流动显示图。他还进一步地解释道“运动流体中小涡不计其数，大的主体运动只由大的湍涡旋转构成，而小的运动却是由大湍涡和小湍涡一起促成。”这是最早对湍流多尺度特征的描述。

图5 达·芬奇[6-7]

图6 达·芬奇手绘的湍流手稿[6-7]

1839年，在德国建筑学院和联合炮兵与工程学校担任液压工程讲师的海因里希·路德维希·哈根(Gotthilf Heinrich Ludwig Hagen，1797-1884，图7)在管道流中以木屑为示踪粒子进行了流动可视化实验，定性地表明“层流”会随着雷诺数的增加“转捩”为“湍流”[8]。之后，他用水在黄铜管中研究流体在管道中的压力损失规律，成功地观测到流体从“层流”到“湍流”的“转捩”过程及其对压力损失产生的影响[9]。他发现当流体速度超过一定阈值后，压力损失不再符合与流量除以半径的四次方成正比的规律(现在我们称这个规律为Hagen-Poiseuille定律)。哈根的研究工作比乔治·斯托克斯(George Gabriel Stokes，1819-1903)在1845年建立完整的黏性流体动力学方程还要早，是最早开展湍流定性和定量实验测量工作的。

图7 哈根(Gotthilf Heinrich Ludwig Hagen)的照片

1880年，英国曼彻斯特大学的理论物理学家雷诺(Osborne Reynolds，1842-1912，图8)在著名的圆管染色液流动显示实验中(图9)引入一个无量纲的常数Re=ρUD/μ，这个常数在1908年被德国物理学家阿诺德·索末菲(Arnold Sommerfeld，1868-1951)提议称为雷诺数。雷诺在实验中发现，在雷诺数超过一定数值后，圆管流动从层流转变为湍流。这一成果在1883年发表在英国皇家学会会刊上[10]。1895年，雷诺从N-S方程(Navier-Stokes equations)出发，提出将描述湍流流动的速度、压强等物理量分解为系综平均量和脉动量之和，将他们代入N-S方程，并对方程两边取系综平均，得到描述湍流平均运动的雷诺平均方程，开创了对湍流平均量进行定量动力学理论研究的工作。

图8 作者在英国曼彻斯特大学校内拍摄的雷诺肖像及其实验用水槽、其本人研究成果和著名的“雷诺实验”[10]示意图

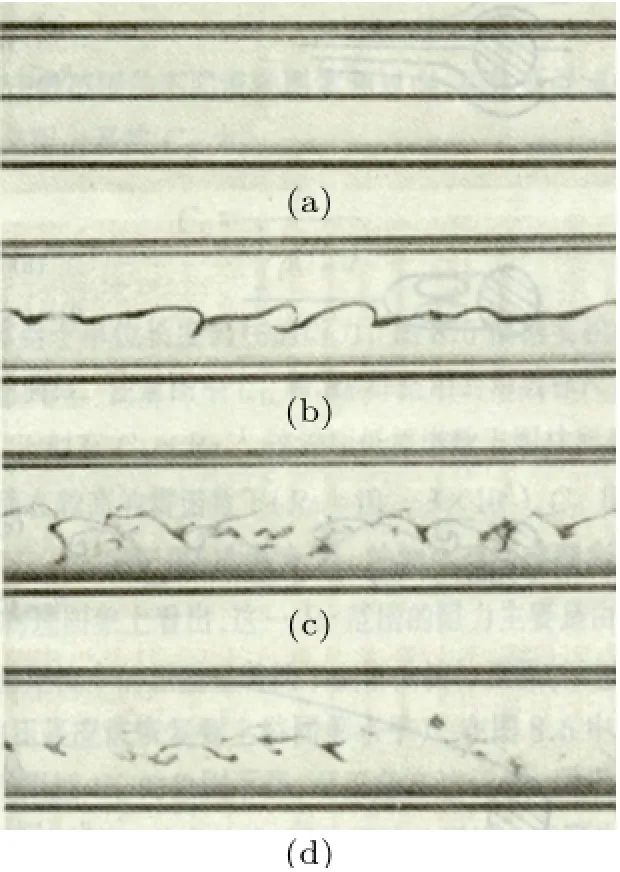
图9 圆管染色液流动显示实验(由图(a)到图(d)，管中流体的流动速度依次增大，相应的雷诺数也依次增大)

3 湍流边界层

流体边界层的流动是不稳定的，在边界层刚刚形成的阶段，是层流边界层，流体还是非常有序的流动，但是层流边界层是不稳定的，固壁上或者外界的扰动会导致层流边界层失稳，流动变得逐渐混乱起来，最终转捩为湍流边界层。图10是一个流体流过固体壁面形成的边界层发展演化的示意图。

图11 是湍流边界层的瞬态流动显示照片，湍流边界层内是非常混乱的流动，而且它的外边界是不规则的，也是随时间不断变化的。

在20世纪50年代以前，科学界普遍认为湍流就是流体质点完全随机无序的混乱运动。美国斯坦福大学的Kline(图12)小组在1967年用氢气泡流动显示的方法[11]，对湍流近壁区结构进行全面细致的观测，发现了湍流大尺度相干结构规律的“猝发”现象。湍流大尺度拟序结构(又称相干结构)的发现是湍流研究史上的一个重大突破。它极大地改变了学界对湍流本质的认识：湍流中不仅有随机的成分，而且存在有结构的有序成分。湍流是“随机”与“有序”并存的高度非线性复杂系统。相干结构在湍流产生、维持、发展、演化的过程和机制中起着重要作用。著名流体力学家李普曼(Liepmann)说过，“工程技术中的大量问题与湍流相干结构密切相关”，“湍流中存在相干结构的最重要方面(意义)也许是以干扰这种大尺度结构来控制它(自己)”[12]，也即预言了“人们可以通过控制相干结构来控制湍流运动”。

图13 是经过数字图像处理的湍流边界层近壁区大尺度相干结构的氢气泡流动显示图像。可以看到大尺度流向涡旋结构的强烈旋转现象。从这里我们就明白了前述唐诗中“北风卷地白草折”，“随风满地石乱走”，“卷我屋上三重茅”这些自然现象的原因

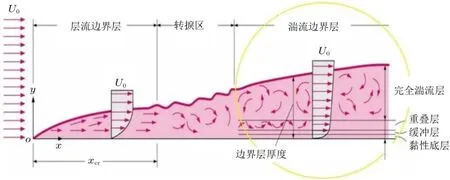
图10 流体流过固体壁面形成的边界层发展演化的示意图

图11 湍流边界层的瞬态流动显示照片

图12 美国斯坦福大学的Stephen Kline教授[13]

图13 湍流边界层近壁区大尺度相干结构的氢气泡流动显示图像[14]

了。正是狂风吹过地面以后，形成的大气湍流边界层内的大尺度相干结构(或超大尺度结构，very large scale motions，VLSMs)的强烈旋转和剪切，使得地面上的物体被风中强烈而复杂的涡旋不断卷折，形成了“北风卷地白草折”，“随风满地石乱走”，“卷我屋上三重茅”这些自然现象，这正是诗人对这些自然现象细致入微的观察和栩栩如生的描写。一般地，大气边界层风场雷诺数Reτ约为O(106)量级，当大气表面层含沙风场平均风速约为13 m/s(6级强风)时，边界层厚度δ约为430 m，其中形成的VLSMs在展向如蛇状蜿蜒摆动，其流向尺度可达1.3 km以上，对湍流能量、雷诺应力以及物质输运等的贡献显著大于其他相干结构[8]。有趣的是，VLSMs的演化在近地表主要是“自下而上”的上卷结构，而在大气表面层主要是“自上而下”的下卷结构，这也解释了诗人描述的“北风卷地白草折”等自然现象[8]。

湍流边界层相干结构在自然界还有很多表现形式，风吹过地面形成的(超)大尺度相干结构，是沙尘能够被吹离地面产生沙尘暴的原因(图14)，沙尘暴风场中的VLSMs主导了沙尘的输运[8]。图15是河床底部的湍流相干结构形成的沙丘，相干结构也是河床底部泥沙起动的原因。图16是风吹过沙漠以后，在沙漠上留下的湍流边界层相干结构的“脚印”。

图14 沙尘暴中的大气湍流边界层相干结构

图15 河床底部的相干结构形成的沙丘

图16 风吹过沙漠以后，在沙漠上留下的湍流边界层中相干结构的“脚印”

自然界中的很多现象都与力学原理有关，我们只有认真地观察自然，认识自然，才能认识这些自然现象所蕴含的力学原理，并体会到热爱自然、观察自然、认识自然、学习自然、与自然和谐相处的乐趣。

致谢感谢北京大学武际可教授、南京航空航天大学明晓教授、天津大学王振东教授和白玉川教授为本文写作提供的帮助。本文除特别注明外，图片均取自网络，仅作为科普教育使用，特此致谢。