利用人工神经网络进行纹样重构与创新

沈淑敏，施清清，孙梦洁，林 丽，陶 晨

(绍兴文理学院 纺织服装学院，浙江 绍兴 312000)

纹样是纺织品的重要构成要素之一，纹样的数字化和自动化生成，是纺织纹样领域的研究热点。目前，数字化纹样技术主要源于数学模型的可视化，其中最重要的是分形算法，如迭代函数系统[1-2]、Julia集[3-4]、L系统[5-6]，均可产生新颖的、别具一格的图案；其次是利用弱混沌系统[7]，包括准规则斑图[8]、均匀随机网[9]、哈密顿函数[10]等来生成纹样图案；其他生成图案的方法还包括傅里叶变换[11]、参数化模型[12]等，这些方法用于纹样创造(Creation)，可以产生新奇、有特色的图案。但针对现有纹样进行数字化改造(Innovation)，且在一定程度上保留原纹样特征的新纹样，未见系统性方法。纹样改造和纹样创造同样重要，特别是对于经典传统纹样，有效地实施纹样改造可为其注入新的生命力，是传统文化保护和发扬的重要途径。本文利用神经网络对现有纹样进行学习和改造的方法，通过将人工智能方法用于纺织纹样的学习与重构，为纹样的数字化创新开辟新的途径。

1 研究方法

1.1 网络模型

纺织纹样可视为一个关系函数F，该函数描述纹样中位置与颜色之间的关系，由式(1)表示：

C=F(P)

(1)

式中：P为纹样在图像中的位置；C为位置P处的颜色。

如果能掌握纹样的关系函数F，就可以在各种条件下重建纹样。关系函数F通常是非常复杂的，不能用简单的数学公式描述，但可以通过人工神经网络来学习和逼近。神经网络结构见图1。

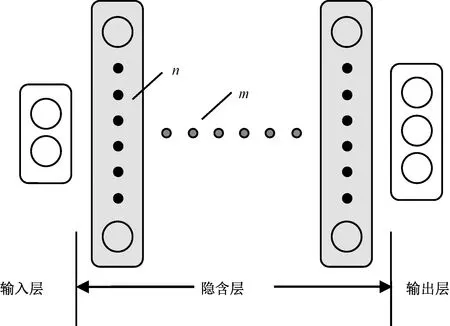
图1 神经网络结构

如图1所示，该网络包括一个输入层、一个输出层和若干隐含层。输入层包含2个神经元，分别接受x、y坐标值输入；输出层包含3个神经元，分别输出颜色r、g、b(红、绿、蓝)分量值；隐含层用来容纳输入、输出层之间的关系模型F，其规模为n×m(n为每个隐含层所含神经元个数，m为隐含层数量)。由于输入和输出层神经元个数固定，隐含层的规模实际上决定了该网络的规模。

该网络的规模(即隐含层规模)可根据纹样的复杂程度而定，复杂程度主要取决于纹样中包含的颜色数目。如果网络不能输出令人满意的结果，则可以扩大隐含层的规模。

另外，此网络结构中的输入和输出值都应被标准化，以保证输入/输出数值落入范围0～1内。坐标值x、y分别除以纹样的宽度和高度进行标准化，颜色分量r、g、b则除以最大值255。

1.2 纹样重构

纹样学习就是训练神经网络用来逼近关系函数F。纹样重构是指当网络完整学习关系函数F后，利用它的输出来重建纹样。

纹样图像中的每个像素对应一个输入样本，该样本即为对应像素的坐标值，其样本标签为对应像素的颜色值，如此1个纹样构成1个训练样本集。纹样图像构成训练样本集见图2。

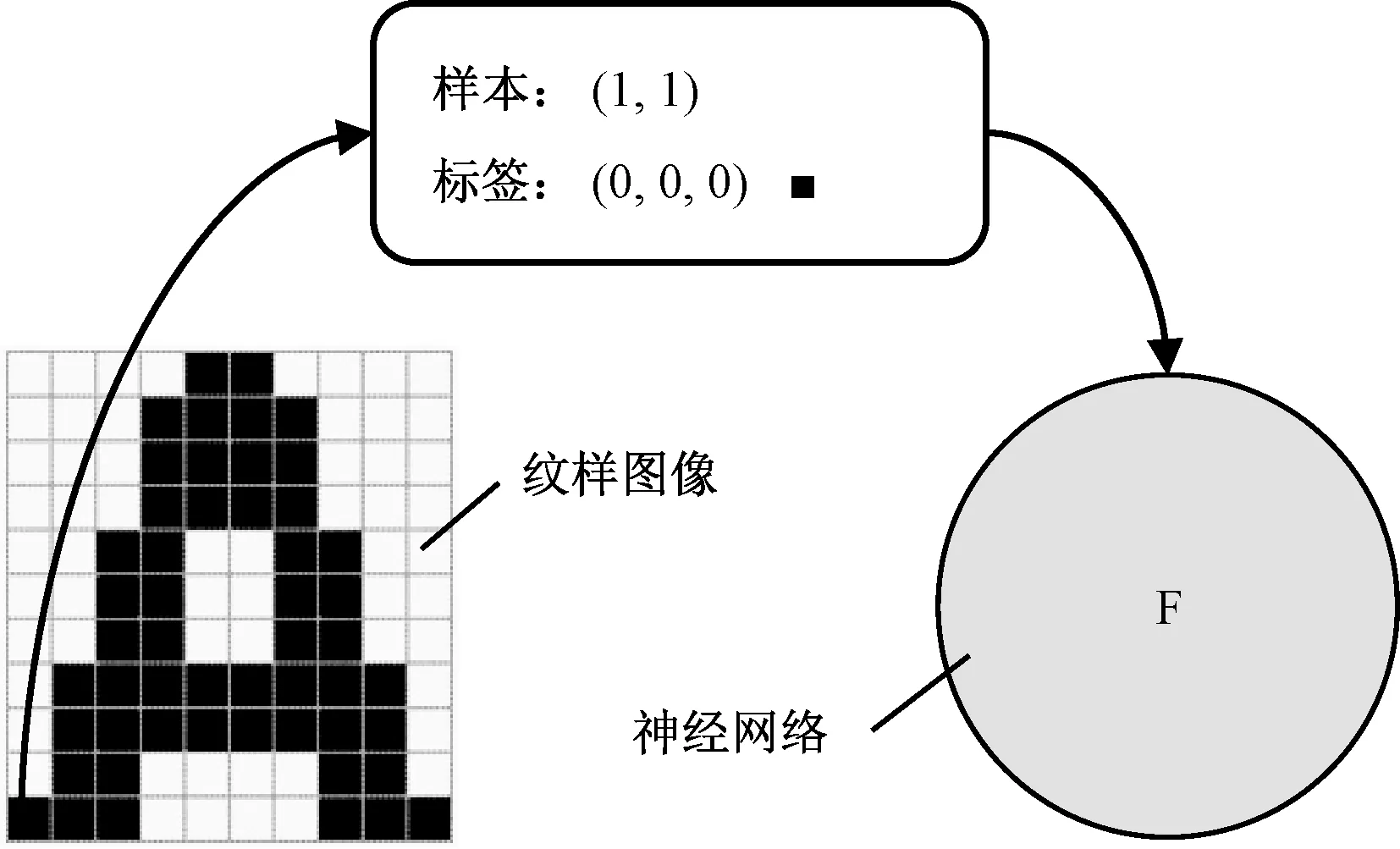
图2 纹样图像构成训练样本集

使用该样本集反复训练网络，采用反向回馈方法使网络输出与样本标签之间的误差不断减小，最终落入可接受的范围内，即完成了纹样学习。纹样学习过程中的误差变化见图3。

图3 纹样学习过程中的误差变化

由图3可以看出，随着训练次数的增加，总体误差不断减小，逼近0。当误差降低到一定程度，即可认为网络完整学习了纹样(即关系函数F)。一对坐标输入，就会得到该坐标上的颜色输出。纹样重构见图4。将这些颜色输出重新置于对应的坐标上，便完成了纹样重构。

图4 纹样重构

一般地，训练次数越多，网络输出误差越小，重构后的纹样与原纹样越接近。如果网络输出的误差足够小，该网络称为学习完善(Well-learnt)的网络，如图4(d)对应的网络；否则称为学习未完善(Poor-learnt)的网络，如图4(b)对应的网络。这2种网络之间没有绝对的界限，但纹样创新应该在学习完善的网络上进行，以尽量保留原纹样在造型或颜色上的一些特征。

1.3 纹样改造

当神经网络在一定程度上完整学习了关系函数F，可在网络的输入/输出层上插入干扰函数，对输入/输出值进行调制，实现纹样的改造和创新。干扰函数可以是任意函数，唯一的条件是其值域必须在0～1范围内，以适应网络模型对输入/输出值的要求。输入干扰见图5。

图5 输入干扰

在输入层上，原输入值x、y先经干扰函数处理并产生新的输入值x′、y′，再将新的输入值传递给神经网络。因此，输入干扰可定义为：

x′=Ix(x,y,r,g,b)

y′=Iy(x,y,r,g,b)

(2)

式中：Ix、Iy分别为原变量x、y上的干扰函数；x′、y′为相应干扰函数的结果变量；x、y、r、g、b为干扰函数中所涉及的变量，即参考变量。

通过输入干扰进行纹样改造，见图6。

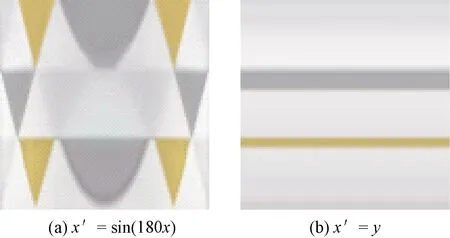
图6 输入干扰改造后的纹样

在图6(a)中，原变量x上的干扰函数利用正弦算子实施干扰，产生了具有对称特征的新纹样。该例中原变量y上的干扰函数实际为y′=y，如果某个干扰函数其结果变量等于原变量，则省略不写。图6(b)中，原变量x上的干扰函数将另一个原变量y赋予结果变量，实际上是对原纹样的对角线特征进行横向扩大。这2个纹样都是在图4(b)所对应的网络(即学习完善的网络)上施加干扰和输出的。同理，可以在输出层上插入干扰函数。原输出值r、g、b经干扰函数处理并产生新的输出值r′、g′、b′，再根据新的输出值进行纹样重构。输出干扰见图7。

图7 输出干扰

输出干扰可定义为：

r′=Ir(x,y,r,g,b)

g′=Ig(x,y,r,g,b)

b′=Ib(x,y,r,g,b)

(3)

式中Ir、Ig、Ib分别为原变量r、g、b上的干扰函数。

通过输出干扰进行纹样改造，见图8。

图8 输出干扰改造后的纹样

图8(a)中，原变量r上的干扰函数以坐标x为其中一个参考变量实施干扰，对纹样中的红分量的横向分布进行了调整。图8(b)则同时对颜色变量r、g进行干扰，使得纹样中的红、绿分量的横向和纵向分布发生了变化。可见，输入干扰通过重塑造型进行纹样改造和创新，而输出干扰则是通过调整颜色分布的方式进行纹样改造的。干扰函数中可以涉及的参考变量包括所有输入和输出变量。

2 结果与讨论

2.1 网络模型中的坐标形式

在本文研究中，将纹样看作一个位置P与颜色C之间的关系模型，使用人工神经网络学习该模型，从而能够重构纹样，以及进一步改造纹样。如前所述，位置P由一对直角坐标(x,y)表示，但也可用其他形式表示，如极坐标(由极径l和极角θ确定)。极坐标下的纹样重构与创新见图9。

图9 极坐标下的纹样重构与创新

图9(a)为训练8 000次后的输出结果。图9(b)中，原变量θ上的干扰函数以θ为参考变量，利用正弦算子实施干扰，产生的纹样具有对角线对称性质。图9(c)中，原变量l上的干扰函数将参考变量θ直接赋予结果变量，其结果纹样实际是原纹样中所有数值满足l=θ的点以左上角为中心的放射性扩展。图9(d)是一个输出干扰的例子，以θ为参考变量对颜色变量r实施干扰，使得结果纹样中的红分量在不同角度上的分布发生了变化。

同样，颜色C除用RGB颜色(“红/绿/蓝”颜色)表达外，也可采用其他形式表达，如HSV颜色(“色调/饱和度/亮度”颜色)。HSV颜色下的纹样重构与创新见图10。

图10 HSV颜色下的纹样重构与创新

图10 (a)是在HSV颜色下训练8 000次后网络输出的结果。图10 (b)是借助HSV颜色进行输出干扰的结果，以坐标x、y为参考变量，利用if算子和正弦算子复合形式对颜色变量v实施干扰，使得结果纹样出现了因明度变化引起的纹路。if算子的作用是条件选择，它有3个参数，第1个参数是1个条件表达式，当该表达式成立时取第2个参数值，否则取第3个参数值。

总之，对图1网络结构，存在2种输入形式(即直角坐标x、y输入和极坐标l、θ输入)和2种输出形式(即RGB颜色输出和HSV颜色输出)。

2.2 纹样重构的影响因素

如前所述，通过训练可使神经网络完整学习纹样关系模型，然后将网络输出置于对应的位置上，实现纹样重构。试验发现，极坐标形式下纹样学习过程与直角坐标形式类似，即总体误差随着训练次数的增加而下降并逼近0。图9(a)和图4(d)同为训练8 000次后的输出结果，其图像质量基本相当。

颜色表达方面，在神经网络中使用HSV颜色进行学习和重构，其效率和精度不如使用RGB颜色，图10 (a)与图4(d)相比精度较低。数字图形设备(如电脑显示器)基本上都使用RGB颜色，因此神经网络中的HSV数据需要经过2次转换，第1次是构造训练样本时将数字设备上的RGB数据转换成HSV数据，第2次是在网络输出后要将HSV数据转换成RGB颜色以便在显示器上绘制。由于RGB颜色与HSV颜色并不一一对应，2次转换导致的精度损失使得HSV颜色下的纹样重构不能令人十分满意。

此外，纹样重构的结果与训练次数和网络规模有关。训练次数对纹样重构的影响已由图3、4显示。给定训练次数t=8 000，不同网络规模下的纹样重构见图11。其中时间耗费(s)除以最大值进行标准化处理。

图11 不同网络规模下的纹样重构

由图11可以看出，在同样的训练次数下，网络规模越大，逼近能力越强，输出纹样与原纹样越接近，但时间耗费也越多。过大的规模可能不是必要的，图11(c)(d)显示的重构纹样差异非常微小几乎可以忽略，但耗费时间有显著不同。经验表明，如果网络输出长时间内不能达到训练目标，则应扩大网络规模。扩大网络规模不会引起所谓“过拟合”问题，因为该网络并不需要应用到新的纹样上，即它不需要适应新的样本。

2.3 纹样创新

如前所述，通过在网络的输入/输出点上插入干扰函数，对位置/颜色值进行调制，可实现纹样创新。对位置输入的干扰带来纹样造型的改造，而对颜色输出的干扰带来纹样色彩分布的改造。纹样改造能够产生非常丰富、新奇的图案，再结合简单的镜像处理，即可得到四方连续的纺织纹样。镜像处理见如图12。

图12 镜像处理

这种利用干扰函数实施的纹样改造不是随机、不可控的，其是有规律、可控的。本文总结几种典型的纹样改造方式及其对应的干扰函数。

2.3.1 条纹化

条纹化是指提取原纹样中的直线或曲线特征构成新的条纹纹样，这是通过输入干扰实现的，图6(b)、图9(c)都是条纹化改造的例子。条纹化改造的关键是，某个输入变量上的干扰函数以另一个输入变量为唯一参考变量。条纹化改造效果见图13。生成的纹样已经过镜像处理。

图13 条纹化改造效果

图13(a)、(b)中，输入变量y上的干扰函数以另一个输入变量x为唯一参考变量。图13(c)、(d)中，输入变量θ上的干扰函数以另一个输入变量l为唯一参数。它们的干扰函数中都使用了幂指数算子或三角算子。幂指数算子和三角算子是干扰函数中的基本算子，它们能保证计算结果在0～1范围内，此外三角算子的周期性还能带来图案上的对称和重复。

2.3.2 扭曲化

在输入干扰中，如果某个输入变量上的干扰函数同时依赖2个原输入变量，结果纹样呈现扭曲效果，扭曲化改造效果见图14。

图14 扭曲化改造效果

图14(a)中，输入变量l上的干扰函数被指定为2个原变量l、θ的复合运算形式，其中指数上的三角运算单元的绝对取值是为了保证其介于0～1内，从而结果变量也介于0～1之间。图14(d)中对原变量x、y分别实施干扰，干扰函数都以2个原变量为参考变量。

2.3.3 沙 化

沙化是借助rand算子实现的一种随机效果，rand算子的作用是生成0～1之间的均匀分布的随机数。沙化改造效果见图15。

图15 沙化改造效果

图15(a)是在图14(a)所示纹样基础上进行的沙化处理，使用rand算子对输入变量θ实施干扰。图15(b)是对图13(b)所示纹样进行沙化，使用if算子有选择地对纹样中的某些区域进行处理。

2.3.4 叠 印

在输出干扰中，如果干扰函数以位置变量(x、y、l、θ)为参数变量，并且使用高频三角算子进行调制，可以得到带有彩色纹路的叠印图案。与条纹化处理得到的纹路不同，这种纹路是色彩因子分布规律性变化带来的。叠印改造效果见图16。其三角算子的频率越高，纹路越细，如图16(a)、(b)所示。叠印处理的另一个特点是，处理灰度纹样也能产生丰富的彩色叠印效果，图16(d)是对图16(c)所示灰度纹样进行叠印处理的结果。

图16 叠印改造效果

3 结 论

本文研究将纺织纹样视为位置和颜色之间的关系函数。使用人工神经网络学习该关系函数，利用网络输出重构纹样，可取得与原纹样非常接近的效果。通过在网络输入输出层上设置干扰函数来进行纹样改造和创新，可获得非常丰富的纹样效果。

①在网络模型方面，采用1个输入层(2个输入点)、1个输出层(3个输出点)和若干隐含层的反向回馈网络结构，通过调节隐含层的规模可控制网络容量以适应不同的纹样关系函数。

②在纹样重构方面，从纹样像素构造网络输入样本集，通过反复训练将误差降低到可接受的范围内，将网络的颜色输出重新置于对应位置上实现纹样重构。重构的精度受网络规模、训练时间和样本集颜色模式的影响，网络规模越大、训练时间越长，重构精度越高；在样本集中采用RGB颜色比采用其他颜色(如HSV)获得的重构精度高。

③在纹样创新方面，通过在网络输入输出层上设置干扰函数，对输入输出量进行调制来实现纹样改造和创新。在输入层上设置干扰函数，对输入位置进行调制，可实现纹样造型的改造。在输出层上设置干扰函数，对输出颜色进行调制，可实现纹样颜色分布的改造。通过在干扰函数中包含相应的结果变量、原变量、参考变量及某些特殊算子，可以实现条纹化、扭曲化、沙化和叠印4种主要的纹样改造创新效果。

总之，基于人工神经网络的纹样重构与创新方法，可为纺织纹样的数字化创新提供一条便捷的途径。