深水测试管柱与隔水管的横向承载特性

孙巧雷 李 中 王尔钧 冯 定 陈文康 刘统亮 严淳鳀

1.长江大学机械工程学院 2.湖北省油气钻完井工具工程技术研究中心 3.中海油研究总院有限责任公司

0 引言

海上测试作业是进行海洋油气勘探开发、储层评价的基础，能为海洋油气的高效开采提供直接依据[1-2]。海上测试作业过程中，测试管柱位于隔水管内部，隔水管通过张紧装置与平台连接，测试管柱悬挂在顶驱大钩上，海水、隔水管、环空流体、测试管柱及管内流体组成了海上测试的“管中管”结构体系[3-6]。由于风、波浪、海流等环境载荷的激励，测试水深的增加，深水测试作业易导致隔水管与测试管柱产生复杂的横向动态特性，从而引起测试管柱的弯曲、碰撞、磨损等。

此前，在海上管柱力学方面，国内外研究主要围绕隔水管下入、立管涡激振动、隔水管与井口的耦合作用等方面[7-15]，而测试管柱力学研究则主要集中在地层段[16-17]，近几年海水段的研究才逐渐增多。唐海雄等[18]结合海上高温井测试特性，进行了温度对测试管柱伸缩变化量的研究；谢鑫等[19]应用有限元法，进行了波浪载荷作用下的管柱动力响应分析；杨志等[20]通过建立井筒温度预测模型，进行了深水测试水深变化下循环液温度的变化规律分析；结合深水测试过程，刘康等[21-23]、杨红君等[24]对测试密封插管安全长度的确定、测试作业的运作模式与测试技术、管柱螺纹连接密封、开关井管柱的安全窗口等进行了研究；何玉发等[25]应用Abaqus软件，开展了深水测试管柱的优化研究；刘红兵等[26]通过建立隔水管—测试管柱涡激振动模型，对涡激振动机理、疲劳损伤规律等展开了研究。但现有的测试管柱相关研究主要是集中测试管柱的工艺、管柱连接安全、天然气水合物等方面[27-28]，少有针对隔水管—测试管柱组成的结构进行横向承载特性分析。

笔者针对我国南海测试使用“管中管”体系结构及作业水深超过900 m的特点，建立了考虑内外流体影响下的测试管柱及隔水管横向动态受力模型；应用数值求解方法，研究了隔水管张紧力、测试管柱悬挂力、海流流速及平台漂移量对“管中管”结构横向承载参数的影响，以期为海上安全测试作业的控制提供理论支撑。

1 海水段井筒温压及轴向力计算模型

井筒温度、压力及管柱轴向力分布是进行测试管柱横向承载特性分析的前提，针对海水段多立管的温压场计算，众多学者已开展了研究[29-32]，笔者结合已有的研究成果，应用傅里叶传热定律、多层圆管传热特性、能量守恒方程，建立了海上测试作用海水段井筒的温压场计算模型；结合测试管柱多变截面、内部流体流动等特性，建立了海水段测试管柱轴向力计算模型。

1.1 井筒温度场模型

测试作业海水段的井筒位于泥线以上，测试管柱内部流体与海水间经油管、环空测试液、隔水管进行换热，井筒结构及其剖面如图1所示。为了简化温度场的计算，分析前作如下基本假设：①忽略测试管柱内部流体及环空流体轴向热传导，即仅考虑径向上的传热；②测试作业内部流体、环空流体及其海域的海水温度场是连续的；③测试管柱内部天然气及环空测试液为一维稳态流动及传热，管柱简化为等截面体；④内部流体无逃窜，环空流体充满。

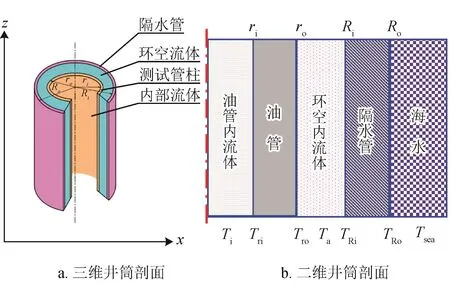
图1 海水段测试管柱井筒剖面图

基于以上假设，管内流体微元与环空流体微元换热量Qia、环空微元与海水微元的换热量Qas方程为：

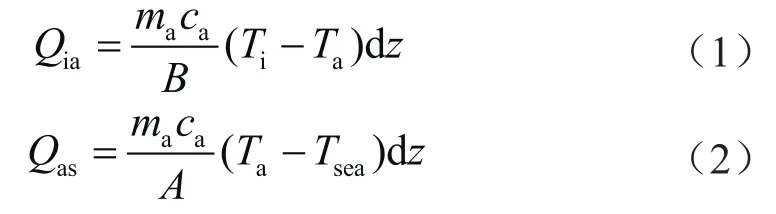
式中ma表示环空流体质量流量，kg/s；ca表示环空流体的比热，J/(kg·℃)；Ti表示测试管柱内流体的温度，℃；Ta表示环空流体的温度，℃；Tsea表示海水温度，℃；A、B表示中间变量，；Ro表示隔水管外径，m；ro表示测试管柱外径，m；Ui表示管柱内流体与环空间传热系数，W/(m2·℃)；Ua表示环空流体与海水的传热系数，W/(m2·℃ )。

对于流体微元的流动，应用能量守恒方程，可得到环空流体及管内流体微元的控制方程，然后通过高斯消元法及齐次微分方程的求解，可获得管内流体温度的解析解：

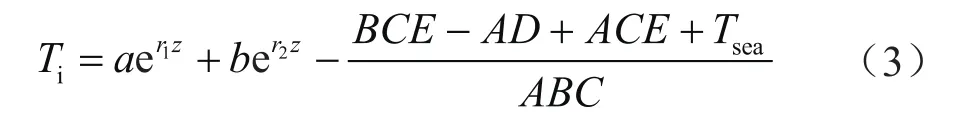
其中

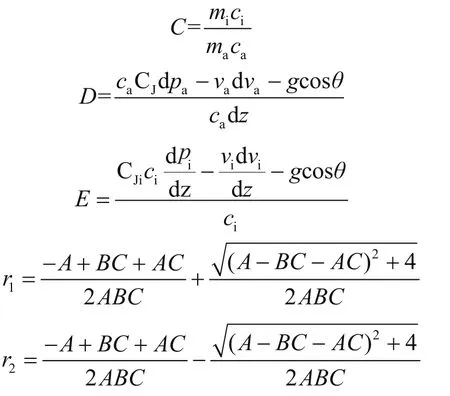
式中a、b分别表示待求量，C、D、E、r1、r2分别表示中间量；mi表示管内流体质量流量，kg/s；CJ表示环空流体的焦汤系数，CJi表示管柱内流体的焦汤系数，ci表示管内流体的平均比定热容，J/(kg·℃)；va表示环空流体流速，m/s；vi表示管内流体流速，m/s；θ表示微元段中心轴线与z轴（垂直于地心）间的夹角，（°）；pi表示管内流体压力，Pa；pa表示环空流体压力，Pa。

该模型的求解需结合井筒压力场及泥线处的环空温度与管内温度进行求解。

1.2 井筒压力场模型

1.2.1 环空测试液压力场

对于测试过程中环空流体的压力，忽略压力对液体性能的影响，简化条件的环空流体压力可按下式计算：

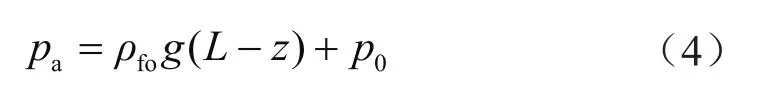
式中ρfo表示环空流体密度，kg/m3；L表示水深，m；p0表示环空井口处压力，Pa。

1.2.2 测试管柱内部流体压力场

由于当前我国深水测试主要以气井为主[33-34]，在考虑内部天然气特性的基础上，可通过分段求解内部流体的压力：

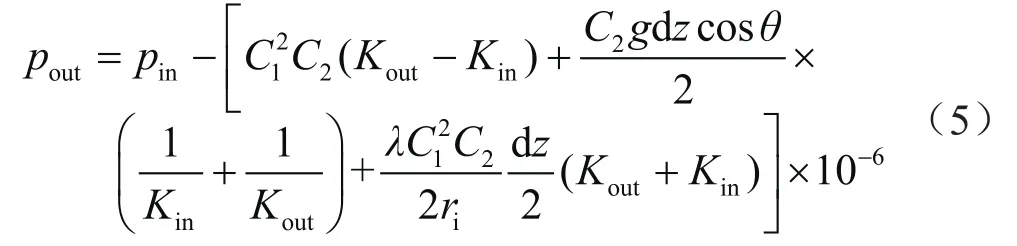
式中pout表示微元段出口压力，Pa；pin表示微元段进口压力，Pa；，qsc表示管内流体当量产量，m3/d；，γg表示管内流体密度，kg/m3；K表示中间变量，，Kin、Kout分别表示进出口计算参数；λ表示管内流体与油管间的流动摩阻系数。

1.3 测试管柱轴向力计算模型

测试作业时，考虑内外流体、截面效应、弯曲效应等对管柱轴向力的影响[35]，忽略测试管柱轴向与横向的方向的夹角，则深度距泥线处zm处t时刻海水段测试管柱单元的轴向力为：

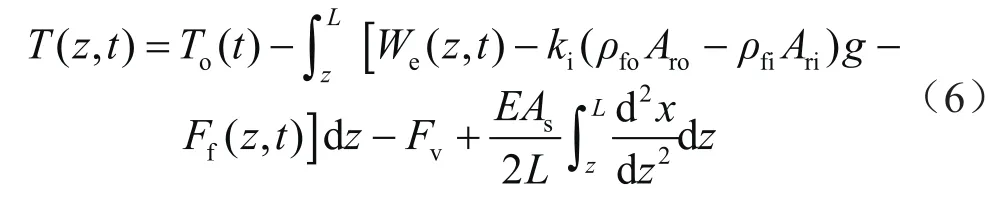
式中To(t)表示的大钩悬挂力，N；We(z,t)表示测试管柱有效浮重，N；表示内外流体压差产生的虚构拉力，N；Ff(z,t)表示内外流体沿管体轴向流动产生的摩擦阻力，N；Fv表示管柱内外变截面引起的附加力[35]，N ；表示管柱横向弯曲产生的附加轴向力，N；ρfo和ρfi分别表示管内、管外流体的密度，kg/m3；Aro和Ari分别管外部、管内部的截面积，m2；As表示管柱有效截面积，m2；g表示重力加速度，一般取9.81 m/s2。

2 “管中管”结构理论模型建立

2.1 管柱微元力学平衡方程

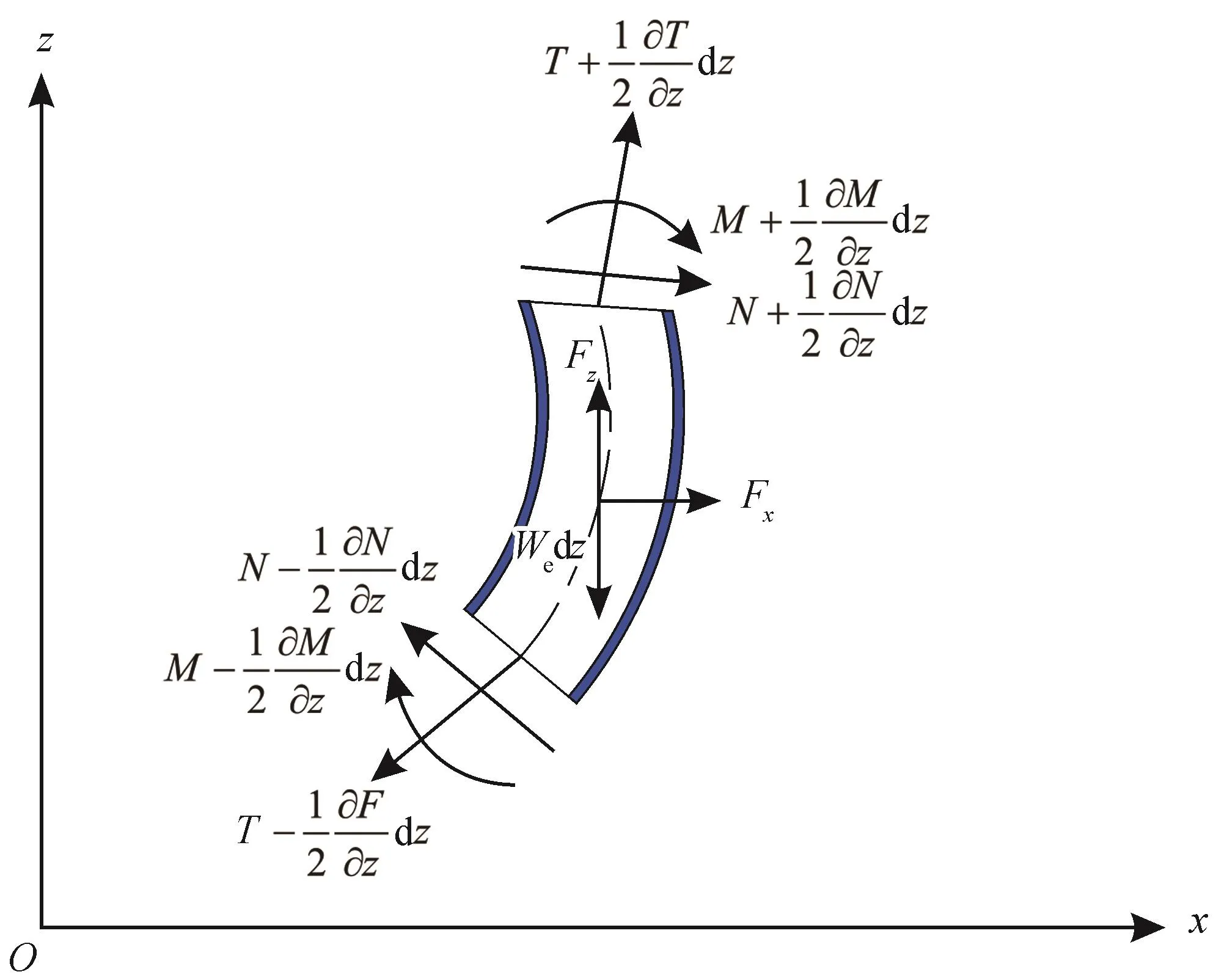
图2 测试管柱微元受力图

海上测试过程中，隔水管和测试管柱的内外壁均与流体相互作用，对于稳定流动下的管柱受力，以测试管柱微元段为例进行受力分析，如图2所示。假设单元为小变形量时，以管柱中心为原点，管柱中点的倾角为，管柱端面的力包括轴向力T、弯矩M、和剪力N，以及内外流体及隔水管对测试管柱微元的横向作用合力为Fx、轴向作用的合力为Fz，管柱重力We。根据单元水平方向上的力学平衡方程，可得：

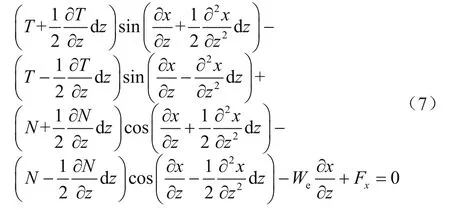
在小变形的假设下，忽略二阶小量，即认为，

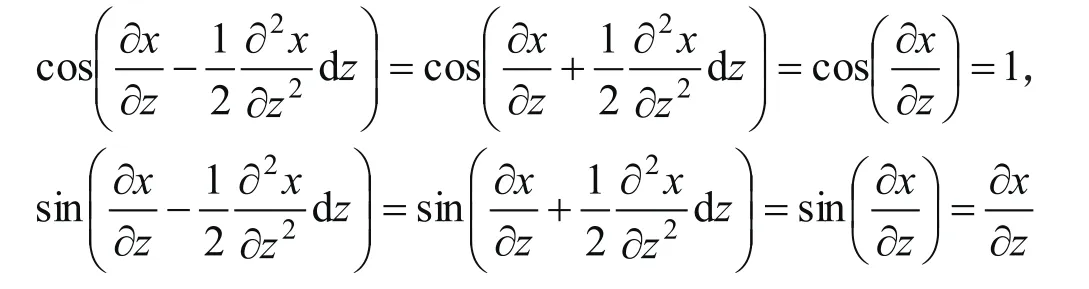
结合材料力学剪力、弯矩、曲率与变形间的关系[36-37]，可得：

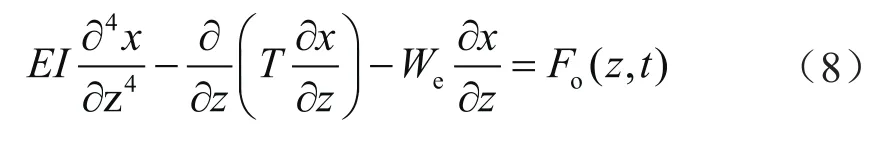
式中E表示测试管柱的弹性模量，Pa；I表示测试管柱惯性矩，m4；Fo(z,t)表示管柱单元的横向综合载荷。

在考虑管柱内外流体惯性力、管柱惯性力、管柱与流体相互作用的横向摩阻分量、隔水管与测试管柱相互作用力、管柱阻尼，管柱微元的横向综合载荷Fo(z,t)可表示为：

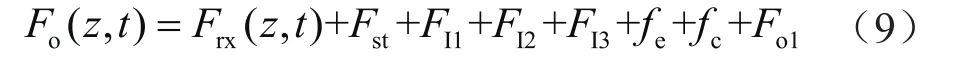
将式（9）代入式（8），最终获得考虑测试管柱与内外流体间相互作用的横向动态微分方程为：

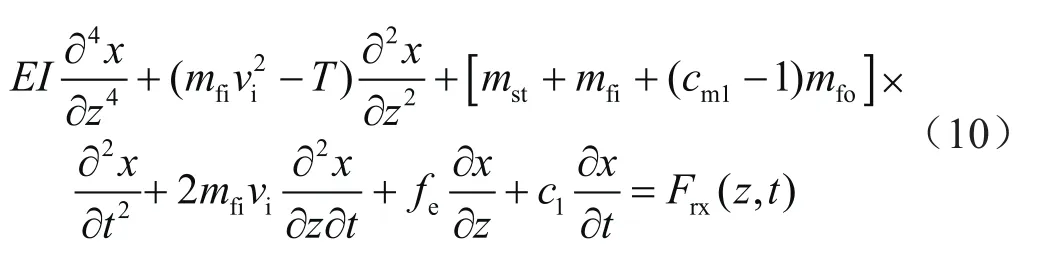
2.2 隔水管横向微分方程

对于测试作业的“管中管”结构体系，分别以隔水管与测试管柱微元为研究对象，建立其力学平衡方程。基于上述测试管柱微元的受力分析，隔水管与其内外流体的横向耦合作用动态微分方程为：

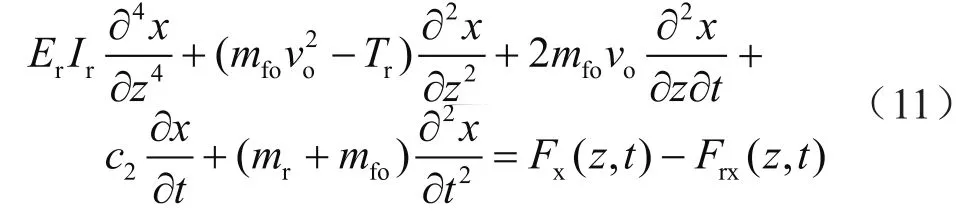
式中Er表示隔水管的弹性模量，Pa；Ir表示隔水管的惯性矩，m4；mfo表示单位长度环空流体质量，kg；mr表示单位长度隔水管质量，kg；vo表示环空流体流速，m/s；c2表示隔水管粘性阻尼系数；Tr表示隔水管轴向力分布，N。

2.3 海水对隔水管作用力

波浪力和海流力的载荷计算可应用莫里森方程表达[38]：

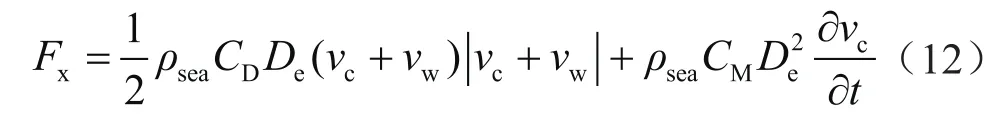
式中De表示隔水管外径，m；vc表示海流引起的水质点横向速度，m/s；vw表示波浪引起的水质点横向速度，m/s；表示波浪引起的水质点横向加速度，m2/s；CD表示拖拽力系数，取值范围介于0.6～1.2；CM表示惯性力系数，取值范围介于1.5～2.0。

3 模型定解条件与求解方法

3.1 模型求解方法

在产量测试过程中，由于环空流体不循环，因体积变化下的相对流速也较小，此时可忽略环空测试液的牵连惯性力、科氏惯性力，则测试过程中的隔水管与测试管柱构成的管柱体系的耦合受力模型为：

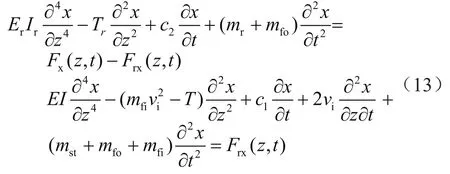
式（13）即为测试作业过程中“管中管”结构隔水管与测试管柱的横向动态受力模型，在隔水管与测试管柱整体产生稳定的横向变形时，此时可将上式联立进行求解。求解前，式中微分方程可应用差分法进行求解，此外还需对整个时间与空间内的求解域进行网格离散，如图3所示。

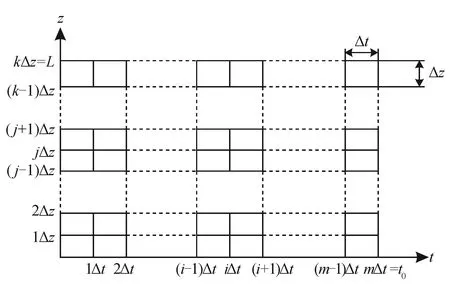
图3 求解网格离散图

在求解域内，各阶导数的计算可用积差表达：

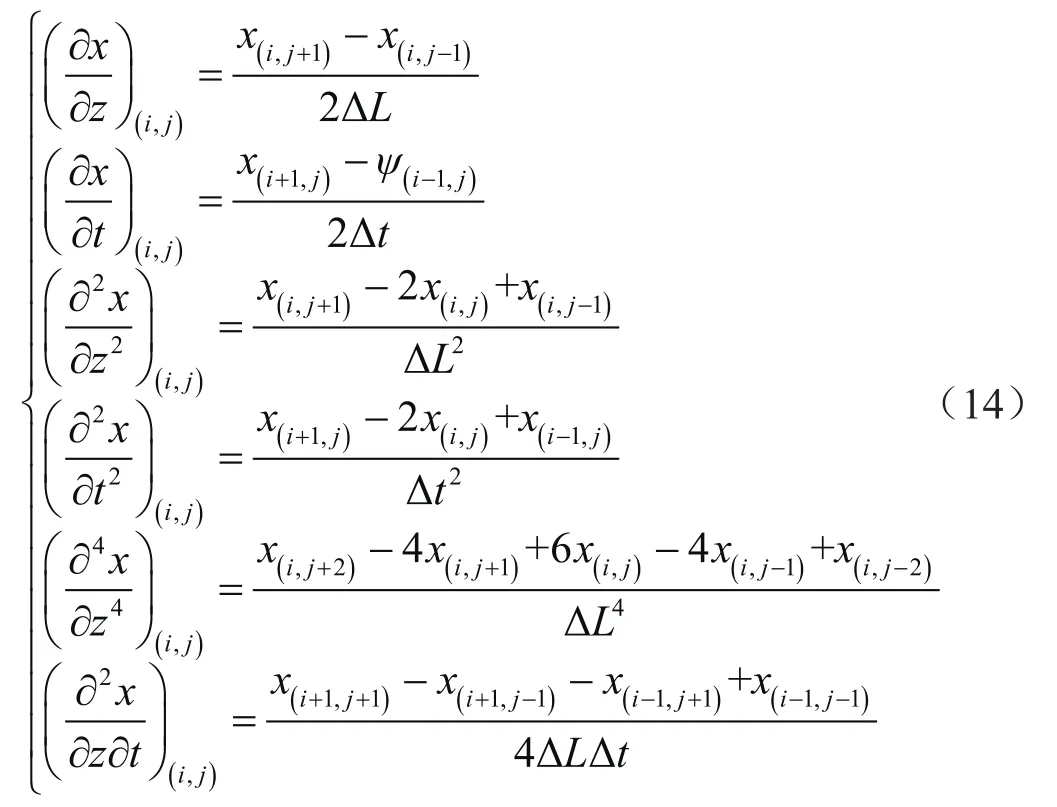
式中ΔL表示空间网格长度，m；Δt表示时间网格长度，s。

同时，在分析计算时，周期性载荷变化下可认为管柱的横向变形具有周期性，即

3.2 模型定解条件

对于测试管柱与隔水管的边界情况，测试管柱上端与平台的大钩相连，下端通过插入式悬挂器与水下井口头连接，在上部补偿情况下，悬挂器可产生小幅转动；隔水管上端与张紧器连接，下端也与水下井口连接，两者下端均可视为铰接，上端可随平台存在一定的漂移[39]。在进行模型求解时，主要分析测试管柱与隔水管的最大承载特性，忽略时间域的影响，并假设两者的最大横向承载一致，其下端边界条件可表示为：

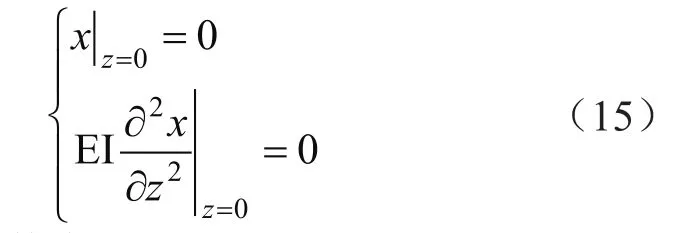
上端的边界条件为：

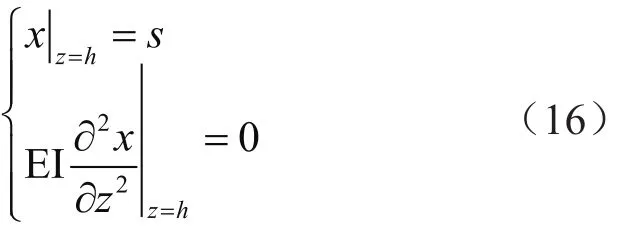
4 实例分析

4.1 相关基本参数

以我国南海已完成测试的某A井为例，该井是典型的深水井，水深为975 m，隔水管设计的初始顶张力大于隔水管柱串的浮重，隔水管与测试管柱的环空流体密度为1 300 kg/m3，作业期间的平均波浪周期约为6 s，波高2.2 m，表层海流速度为0.35 m/s，隔水管外径为533.4 mm，测试管柱外径为114.3 mm，产量为100×104m3/d时，基于井筒温压分布的计算结果，海水段测试管柱内部平均温度为315 K，平均压力为21.95 MPa，对应压缩因子取0.86，计算得管内天然气的平均密度为161 kg/m3，流速为8.37 m/s。对比不同模型下的轴向力计算结果如图4所示，图中考虑内外径及油管浮重、仅考虑油管浮重下的计算没有考虑温压的影响。

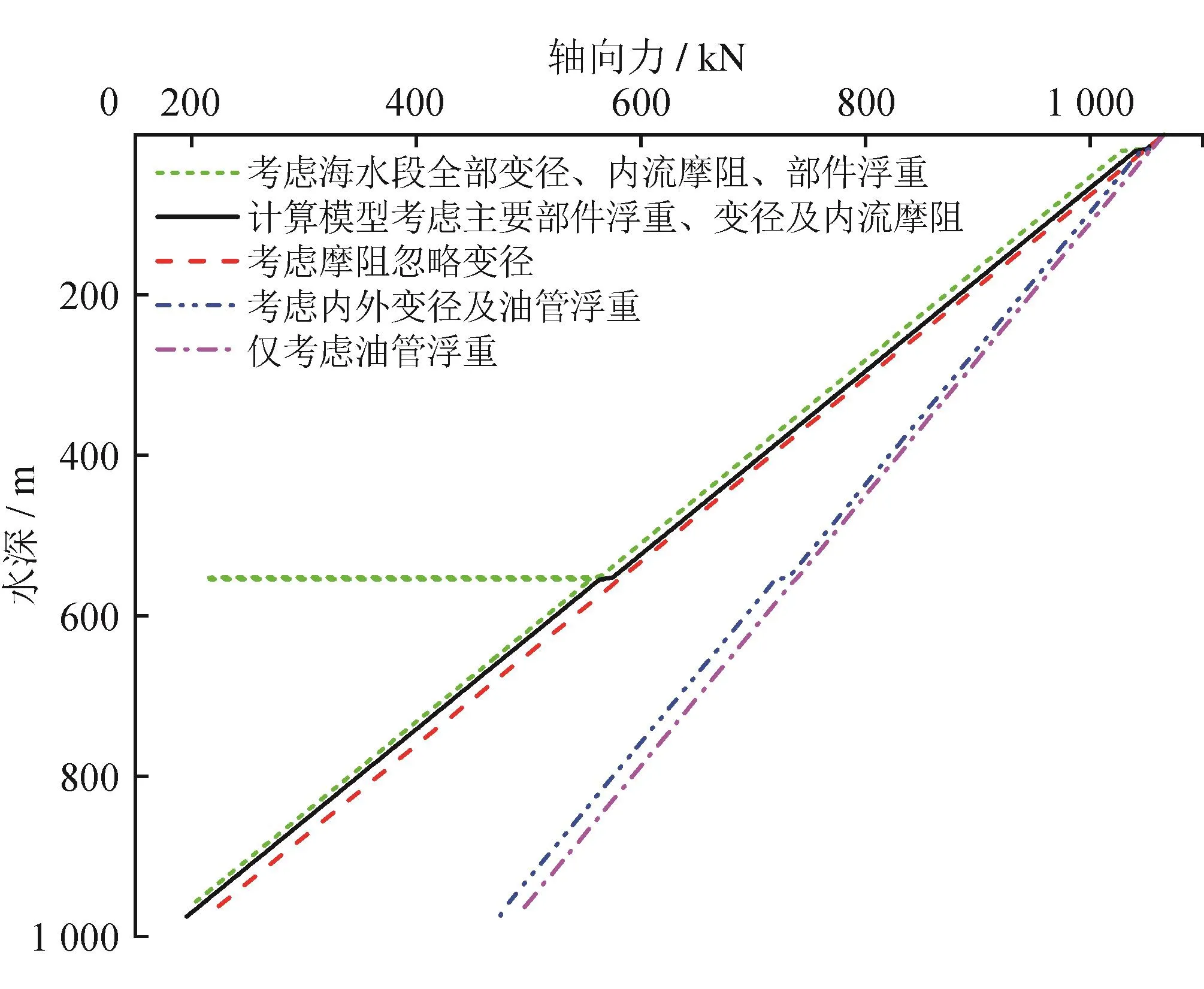
图4 考虑不同因素下轴向力计算结果图

将上述两种结果与考虑温度压力特性下的测试管柱轴向力结果进行对比可知，水深越深，两者的差值越大，由式（10）可知，轴向力的差异性势必引起管柱受力特性的变化，因此，在后续分析中，笔者将考虑温压、浮重、变径及内流摩阻下管柱轴向力模型作为横向动态受力模型求解和承载分析基础。

此外，隔水管、测试管柱作为整体稳定变形时，认为测试管柱、隔水管的位移、转角一致，弯矩变化规律相同。对于海上测试管柱与隔水管的等效应力，可应用第四强度理论进行计算，等效应力σc可表示为：

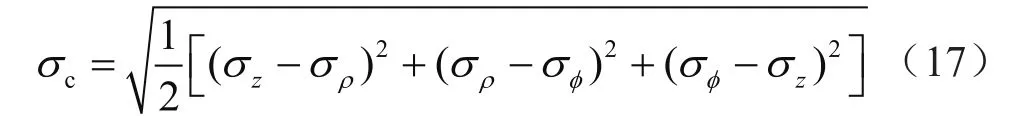
式中σz表示管柱的轴向应力；σρ表示管柱的径向应力；σφ表示管柱的环向应力。

根据相关研究结果[35,40]，隔水管与测试管柱的等效应力随着轴向应力的增大而增大；同时由式（6）以及轴向应力公式和弯矩计算公式，在管柱截面惯性矩一定情况下，弯矩的增长能反映管柱轴向应力的增长，即弯角、弯矩的增大，管柱的轴向应力也增大。在管柱周期性横向变形下，横向位移、弯角、弯矩的增大会导致管柱周期性应力的增大，从而减小管柱的疲劳寿命。因此，本文以隔水管—测试管柱组成的管柱体系的最大位移、最大转角、最大弯矩作为管柱体系横向承载特性进行分析[41]。

4.2 顶张力与悬挂力影响

以隔水管实际重力G为基准，分析顶张力为1.2 G、1.4 G、1.6 G、1.8 G下的横向承载，得到不同顶张力作用下管柱体系的横向最大位移、最大转角、最大弯矩如图5所示。在A井测试管柱坐挂悬挂力为1 066 kN的基础上，以1 066 kN悬挂力波动±20%内进行分析，获得的不同悬挂力下的管柱横向承载参数如图6所示。

由图5、6可知，随着隔水管顶张力、测试管柱悬挂力的增加，隔水管与测试管柱体系各水深处的最大位移、最大转角、最大弯矩均减小；在海平面至泥线100 m处附近，各水深处管柱体系的最大位移、最大转角、最大弯矩的绝对值随顶张力、悬挂力的增大而减小，靠近泥线处相关参数随顶张力、悬挂力增大而增大；在海平面至泥线100 m以上，各水深处的弯矩绝对值随着顶张力、悬挂力的增大而减小，泥线处附近弯矩随着顶张力、悬挂力的增大而增大。

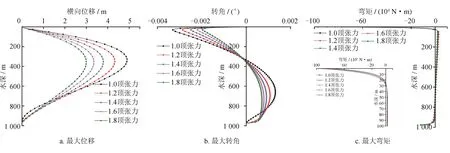
图5 顶张力变化下隔水管—测试管柱体系的最大横向位移、转角和弯矩图

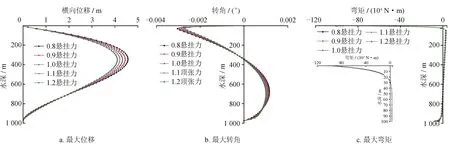
图6 悬挂力变化下隔水管—测试管柱体系的最大横向位移、转角和弯矩图

在隔水管顶张力、测试管柱悬挂力变化时，横向承载相关参数随水深的变化趋势基本一致，增加隔水管顶张力、测试管柱悬挂力均有助于减小管柱体系的最大横向位移，同比例增加顶张力的效果更明显。测试作业增加隔水管的顶张力有助于增加隔水管的横向刚度及振动阻尼、从而减小管柱体系的横向位移、转角及弯矩，在横向最大位移减小的基础上，管柱的振动应力幅值及大小也会有一定的减小[42]。但由于隔水管的张紧力过大也会导致其自振频率、轴向应力的增加，影响隔水管的抗疲劳[43]，因此隔水管的顶张力也不宜过大。

同时将上述结果与隔水管、测试管柱分别受相同海洋环境载荷时的结果进行对比，如图7所示。根据图7相关结果可知，管柱的最大位移、最大转角、最大弯矩在仅考虑隔水管时要大于考虑隔水管—测试管柱体系的值；将海洋环境载荷直接作用于测试管柱时，测试管柱的相关参数要小于管柱体系值，主要是由于海流与波浪对测试管柱截面的作用力、测试管柱的惯性矩等都减小；但对于管柱体系下的测试管柱而言，计算的测试管柱弯矩比将海洋环境载荷直接作用于测试管柱时的弯矩小，因此，将海洋载荷直接作用于测试管柱进行测试管柱力学分析与测试管柱位于隔水管内部的实际工况有较大差别。

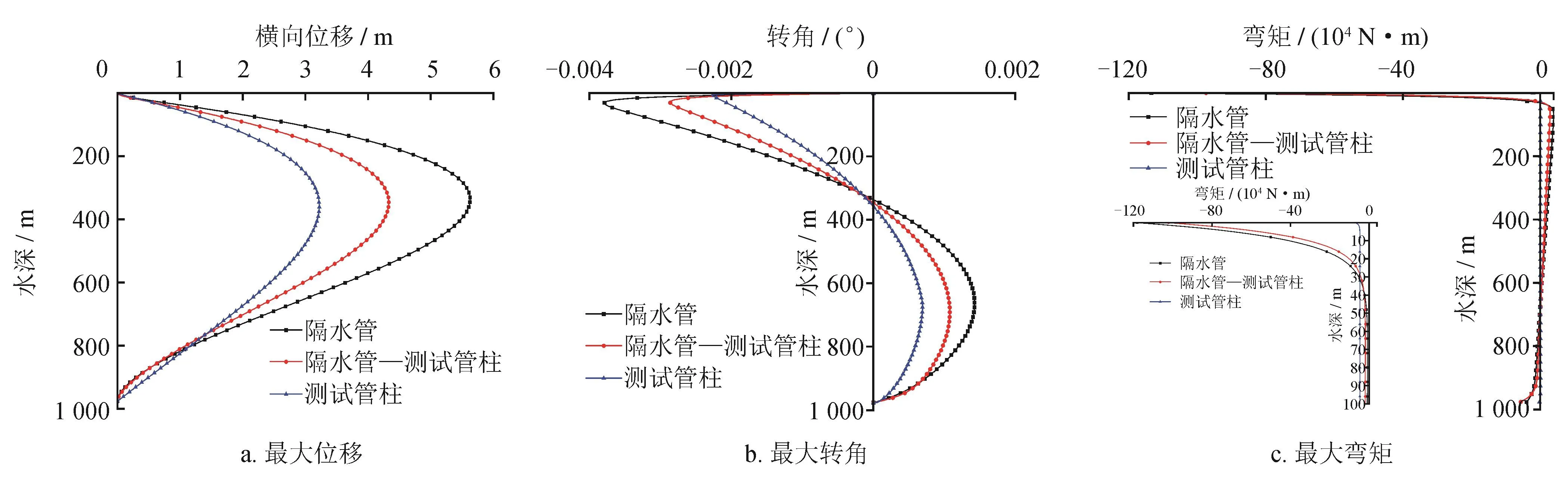
图7 相同海洋环境载荷下立管的最大横向位移、转角和弯矩图

4.3 波浪影响

根据A井作业海域海流参数的统计数据，分析作业区域常规流速、最大流速及不同年限周期所遇最大流速下的管柱体系的横向承载特性，相关海流参数如表1所示，通过计算得到不同海流流速下的隔水管—测试管柱体系的横向承载参数如图8所示。

由图8结果可知：当测试海域海流由0.35 m/s增加到2.27 m/s时，管柱体系各水深处的最大横向位移、转角、弯矩有明显增加，整个管柱参数出现极值点的水深均一定程度上增大，这是由于泥线处海流流速不为0，海流随水深的变化率增大。从总体上看，海流流速对管柱体系的横向承载参数作用明显，测试作业海域海流流速的增加，加大了管柱体系失效的风险，因此，在实际测试作业时一般会根据相关监测的相关海域的海洋环境载荷优选时间，同时现场测试作业也需密切监测作业海域的海流流速，以便应对潜在的风险。

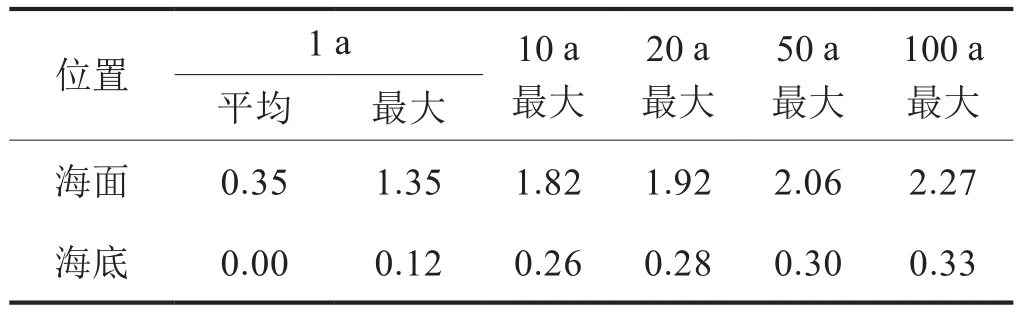
表1 A井海域海流流速统计参数表 单位：m/s

4.4 平台漂移影响

由于海洋环境载荷的作用，钻井平台在测试过程中可能会产生一定的漂移，以A井水深5%范围的5 m、10 m、20 m、30 m、50 m的偏移量进行“管中管”结构体系横向承载特性的研究，相关结果如图9所示。

由图9结果可知，管柱体系的最大位移随着平台漂移量的增加显著增加，管柱体系的最大横向位移幅值逐渐靠近海平面；最大转角及弯矩幅值随着平台漂移量的增加，先减小后增大；主要是由于海流作用使管柱和平台会产生一定程度的横向偏移量，要使平台井口与水下井口对中或作业超过平台自然横向偏移量，均会导致管柱上端悬挂处的弯矩和转角增大；因此，就管柱的理论最大弯矩和转角而言，在测试作业时，顺海流方向使平台产生的合理偏移，会使管柱体系弯角和弯矩减小，在一定程度上能改善管柱体系的承载，以A井为例，平台漂移量为10～20 m间有助于改善测试横向承载。

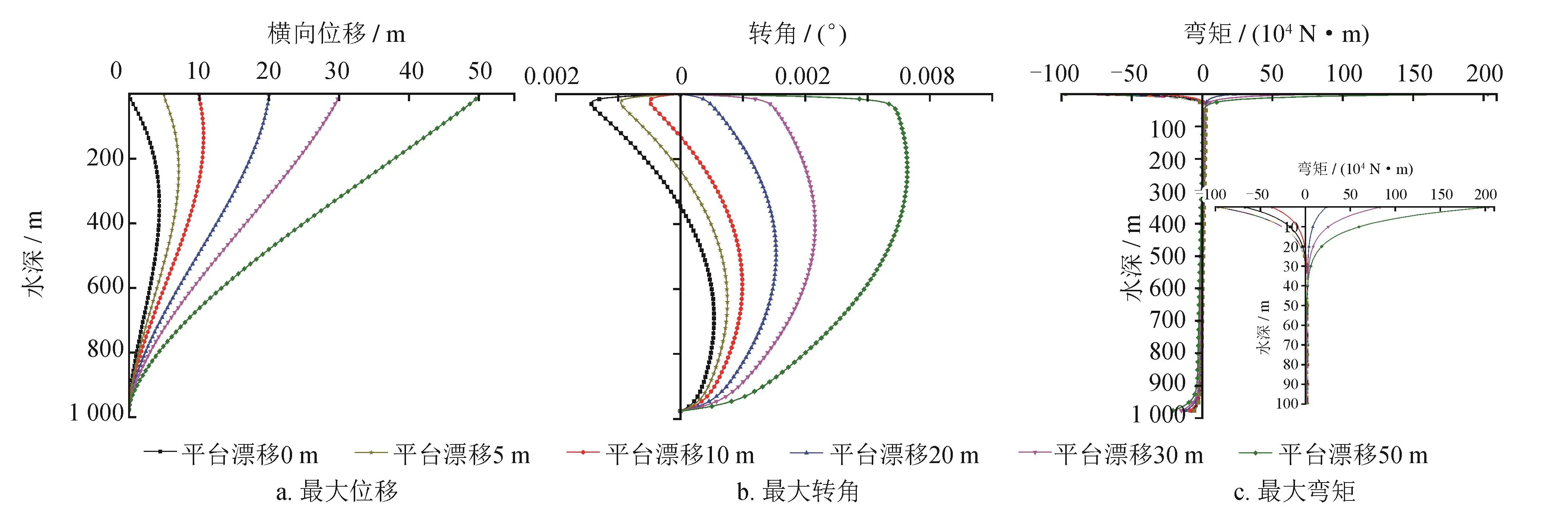
图9 漂移量变化下隔水管—测试管柱体系的最大横向位移、转角和弯矩图

5 结论

1）通过分析海上测试管柱海水段井筒温度传递过程、传热特性，考虑测试管柱内外流体压力的影响，建立了海上测试作业井筒的温压场模型；结合测试管柱内外多变径引起的截面效应、流体流动引起的摩阻效应、弯曲作用产生的附加轴向力等影响，建立了海水段测试管柱的轴向力模型。

2）基于管柱微元的受力模型，考虑内外流体流动下的惯性力、摩阻力、管柱结构惯性力、阻尼等建立了管柱微元的横向受力平衡方程；结合海水、隔水管、环空流体、测试管柱、管内流体构成的海上测试“管中管”结构特点，建立了“管中管”结构隔水管和测试管柱的横向动态受力模型，并结合其边界条件，对模型的求解方法及定解条件进行了确定。

3）基于建立的理论模型，在假设隔水管与测试管柱共同产生横向变形的基础上，分析了海上测试作业过程中测试管柱悬挂力、隔水管顶张力、海流及平台漂移量对管柱体系横向承载参数的影响，相关结果表明：增加隔水管顶张力、测试管柱悬挂力均有助于减小管柱体系的横向承载参数，同比例幅度增加隔水管的顶张力、测试管柱悬挂力，顶张力对管柱横向承载参数的影响更明显；海流流速的增加使得管柱体系的最大横向位移、转角、弯矩增大明显；顺着海流方向平台产生合理的漂移量有助于减小管柱体系的转角及弯矩，以A井为例，10～20 m的平台漂移量为宜。