多级多段细分注水管柱动态力学分析及蠕动规律

黄志宏, 王旱祥, 马珍福, 鲍 蕊,刘延鑫, 魏 振, 兰文剑, 汪润涛

(1.中国石油大学(华东)机电工程学院，山东青岛 266580； 2.中国石化胜利油田分公司科技处，山东东营 257000;3.中国石化胜利油田分公司石油工程技术研究院，山东东营 257000)

细分层注水管柱所在油区储层纵向上层多,层间非均质性严重,渗透率级差高达4～13倍,层间差异加剧,工况趋于多样复杂化,易造成封隔器蠕动失效及管柱永久性弯曲等问题。在管柱力学分析方面,国内外学者的研究主要集中在管柱力学模型及压力温度等参数变化下注水管柱力学状态等方面,李钦道等[1]建立了力学分析模型,讨论了变形受力等问题。温后珍[2]考虑温度、压力及管柱屈曲临界载荷等因素,建立了管柱力学分析模型。蒋敏等[3]针对管柱屈曲、断裂、封隔器失效等诸多安全问题,建立了管柱轴侧向力耦合分析模型。许志倩等[4]完整地描述了整个高压注水过程中管柱力学状态。刘清友等[5]考虑高温高压及复杂井身结构特点,建立了管柱力学分析模型。李敬元等[6]开发了管柱力学分析软件,并进行了初步应用。刘延鑫等[7-8]考虑4种效应以及封隔器的约束条件,探讨了注水管柱的蠕动机制。彭元东等[9]通过开发防蠕动工具,形成了不动管柱多级水力喷射压裂工艺技术。目前对于注水管柱动态力学分析及复杂载荷作用注水管柱蠕动问题少有研究。管柱蠕动会改变封隔器坐封位置及管柱力学状态,易产生胶筒磨损,影响注水管柱的安全性能,甚至会造成封隔器窜动。笔者在考虑井筒三维轨迹及多级多段注水管柱空间受力基础上建立注水管柱三维力学模型,分析封隔器处受力连续性条件和注水管柱动态力学性能,研究封隔器的蠕动机制,提出多级多段注水管柱力学蠕动计算方法。

1 细分注水管柱力学分析模型

分层注水管柱在井筒中受到多种载荷的共同作用[10-16],为真实反映其受力情况,将分注管柱置于三维空间视角中,考虑其所受到的内力(矩)、均布外力、内外流体压力、摩擦及井筒几何轨迹等因素的综合影响,建立分注管柱三维力学模型。

管柱轴线上任一点在切向、法向、副法线方向的单位向量分别用τ、n、b表示,用k0、T0、r表示分注井井筒的曲率、挠率以及管柱与套管间隙。在分注管柱上取s到s+ds之间的微元体,上端点A的井斜角为αi,方位角为φi;下端点B的井斜角为αi+1,方位角为φi+1。假设管柱轴线与井筒几何轨迹一致,分注管柱微元段受力分析如图1所示。

分注管柱在三维空间中各种载荷的联合作用下处于平衡状态,因此对于分注管柱有∑Fi=0, ∑M(Fi)=0。

分注管柱在三维空间中的受力包括[5]:

(1)分注管柱的内力和内力矩。

作用在管柱微元段上部截面上的内力F(s)和内力矩M(s)分别为

F(s)=Fτ(s)τ+Fn(s)n+Fb(s)b,

(1)

M(s)=Mτ(s)τ+Mn(s)n+Mb(s)b.

(2)

作用在管柱微元段下部截面上的内力为-F(s+ds),内力矩为-M(s+ds)。

图1 管柱微元体受力分析Fig.1 Mechanical analysis of string infinitesimals body

(2)分注管柱微元段上的均布力。

分注管柱单位长度浮重Q=qb;套管壁对单位长度分注管柱上的法向正压力N=Ncosθn-Nsinθb;单位长度分注管柱上,由于内外流体作用而产生的黏滞摩阻力为(fi+fo)τ;单位长度分注管柱上,由井筒内壁产生的摩擦力为f1Nτ。

其中q为井筒中管柱单位长度浮重;f1为分注管柱与套管壁之间的摩擦系数;fi、fo分别为内外流体对单位长度分注管柱产生的黏滞摩阻力。

(3)管柱微元段内外流体压力。

内压可以等效为作用在微元段两端截面上的一对轴向压缩力pi(s)和-pi(s+ds)及作用在整个微元段上的向下分布力dFi(s)=(Aiρigk-fiτ)ds;

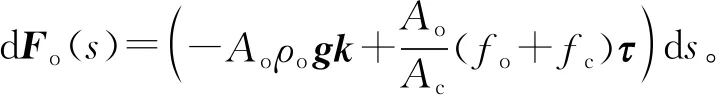
分注管柱在各种载荷的联合作用下处于平衡状态,由此建立力学平衡方程,整理得到:

(3)

其中

Feτ(s)=Fτ(s)+pi(s)Ai-po(s)Ao.

式中,Fτ(s)、Fn(s)、Fb(s)、Mτ(s)、Mn(s)、Mb(s)分别表示分注管柱在τ、n、b三个方向上的分力和分力矩;Feτ(s)=Fτ(s)+pi(s)Ai-po(s)Ao为等效轴力。

(4)

则其轴向力为

Fτ(s)=Feτ(s)-pi(s)Ai+po(s)Ao.

(5)

2 注水管柱蠕动算法

2.1 蠕动机制

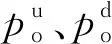
图2 封隔器微元段受力分析Fig.2 Mechanical analysis of packer infinitesimal section

该处的力学平衡方程为

整理得

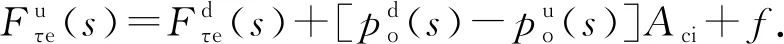
(6)

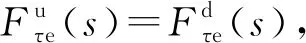
对式(6)进一步整理可得

FΔτ+Fp=f.

(7)

式中,FΔτ为封隔器上、下节点间轴向力之差;Fp为作用在封隔器处的压力引起的力;f为套管壁对胶筒的摩擦力。

在一定范围内轴差力越大,摩擦力也越大,且始终保持FS+Fp=f的受力平衡关系,因此胶筒不会发生移动。但是胶筒有最大静摩擦力,不能无限增大,有最大值fmax,当FS+Fp>fmax,即轴差力大于最大静摩擦力时,胶筒无法继续保持受力平衡,将发生轴向移动,即管柱蠕动现象。

2.2 锚定力及摩擦力确定

为准确计算管柱轴向力分布情况,在胜利油田石油工程技术研究院对SZSM-115水力锚的锚定力及SZSK344-115扩张式封隔器与套管间的摩擦力进行试验。测得锚定力、胶筒摩擦力与工作压差关系如图3所示。

根据实验结果拟合得到水力锚最大锚定力数学模型和扩张式封隔器摩擦力数学模型分别为

Fmd=6.279e-6Δp3-0.002 182Δp2+0.39Δp-12.97,

(8)

Ff=-1.103Δp4+46.48Δp3-565Δp2+4 851Δp+7 856.

(9)

图3 锚定力和摩擦力与注水压差关系Fig.3 Relationship of anchoring force, friction force and water injection pressure difference

2.3 管柱蠕动算法

为准确计算注水管柱在不同工况条件下的蠕动量,应根据图1、2确定注水管柱各节点轴向力,进而依据4个效应理论[7]计算得到胶筒的平衡位置。蠕动量为新的平衡位置与初始位置之间的距离。

细分层注水管柱为多级多段管柱,计算各节点蠕动量时,要考虑各级封隔器处胶筒摩擦力影响。以n级m段注水管柱为例,其有n个封隔器和m个配水器。以封隔器坐封为初始状态,先假定第n级封隔器不发生蠕动,计算第n-1级封隔器受力状态,分析其蠕动情况。若封隔器蠕动则计算第n-1级封隔器自由移动变形及蠕动量,若第n-1级封隔器不发生蠕动,计算管柱的受力变化后再分析第n-2级封隔器受力状态,以此类推,直至第一级封隔器。n级m段注水管柱蠕动计算的算法流程见图4。

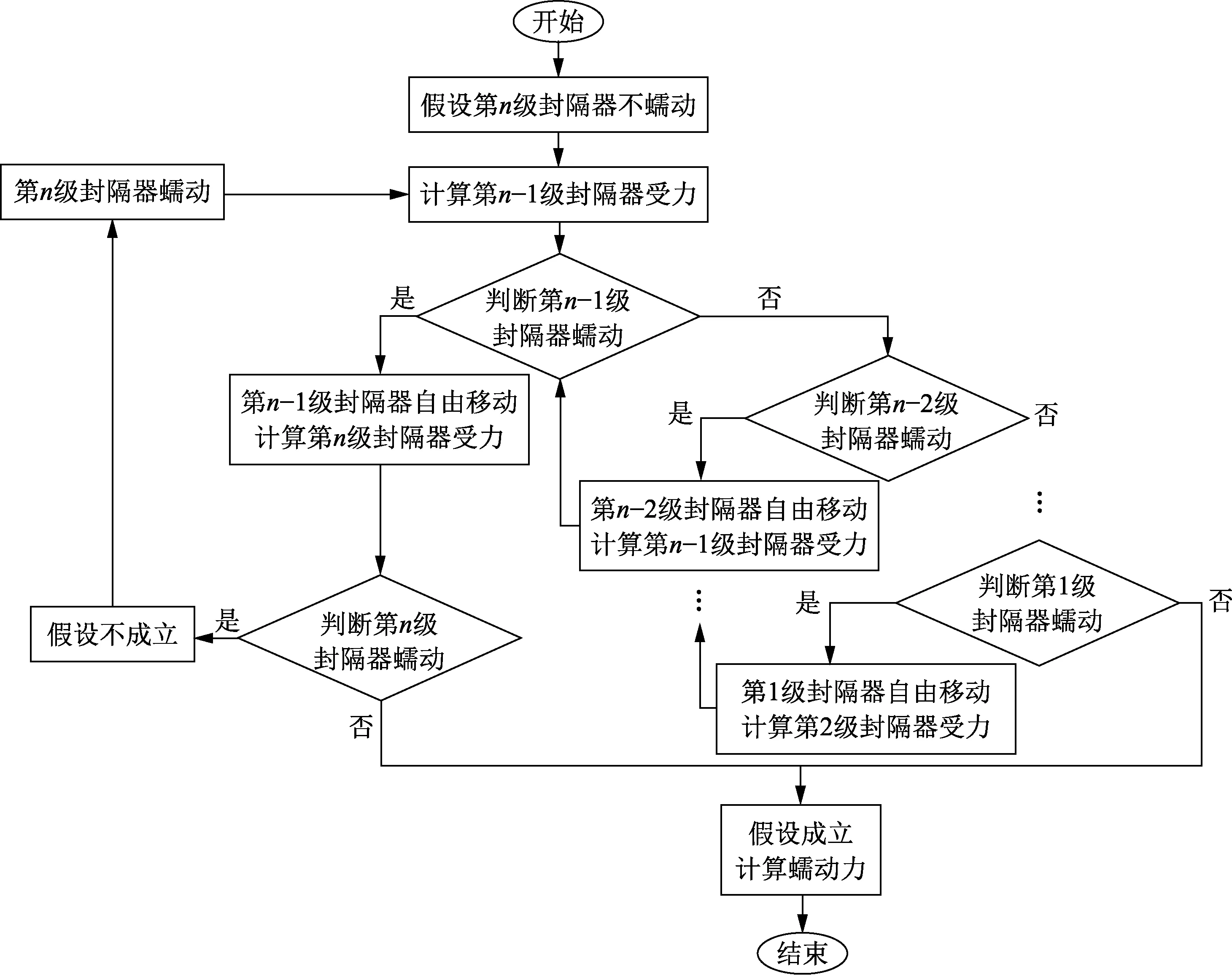
图4 n级m段蠕动分析流程Fig.4 Peristaltic analysis process of n stage and m segment

3 实例验证

对胜利油田河43-12井注水管柱进行动态力学分析及蠕动量计算。该井井深为2 724 m,最大井斜角为53.8°,井眼轨迹如图5所示。注水压力为18 MPa,注入排量为2.5 m3/h,注入液温度为50 ℃。洗井温度为25 ℃,洗井排量为30 m3/h,河43-12井注水管柱由泄油器、封隔器、配水器及筛管丝堵等注水工具组成,共包含3个封隔器及4个配水器,具体管柱结构如图6所示。

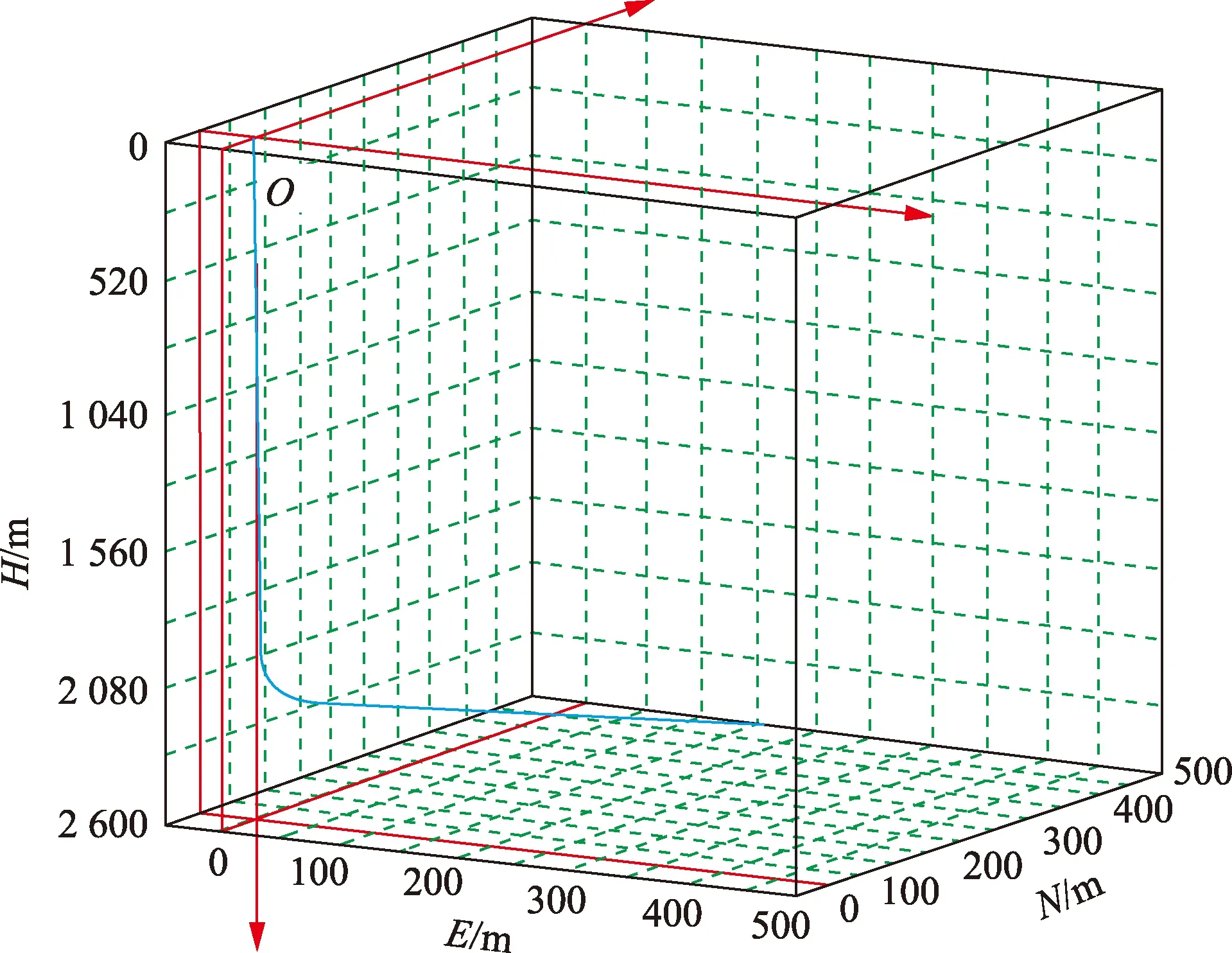
图5 河43-12井眼轨迹Fig.5 Well H 43-12 well track

图6 河43-12分注管柱结构Fig.6 Well H 43-12 pipe string structure

3.1 动态力学分析

现场作业过程中2 d后注水管柱达到稳定状态,故取注水60 h,停注60 h,洗井6 h为计算节点,注水管柱在完成下入和坐封作业后,对分注管柱的力学性能进行动态分析[19]。表1为分注作业工况参数。

表1 分注作业工况参数

图7为注水阶段稳定后分注管柱的力学状态。最大应力位置发生于距井口2 017 m造斜段处,应力达到348.99 MPa;最大轴力出现在井口处,在每一级封隔器处均发生了轴力突变。表2为表1中各作业工况条件下分注管柱的最大轴力、最大应力等力学性能分析结果。由表2可以看出,因注水时管柱有较大的内压,其应力及轴力均大于停注及洗井工况,不同工况转换管柱的受力状态出现明显变化。

表2 各工况分注管柱力学分析结果Table 2 Mechanical analysis result of layered water injection string in every working condition

3.2 蠕动分析

按照表1的工况参数,对河43-12井注水管柱进行蠕动分析,得到注水管柱蠕动规律如图8所示。

注水工况初期,由于注水温度及注水压力变化剧烈,导致轴差力远大于封隔器胶筒所提供摩擦力,管柱收缩向上蠕动明显;停注工况由于井筒温度逐渐回复,管柱伸长向下蠕动几近原始位置;洗井工况受洗井液温度及排量影响,井筒迅速降温,管柱收缩向上蠕动。管柱不施加锚定,该井管柱作业工况全过程向上蠕动0.911 m,管柱蠕动较为明显。由于管柱蠕动不是单一封隔器蠕动,轴向力的传递使得各级封隔器蠕动量相差不多,因此各级封隔器蠕动量随时间变化规律一致。

图7 作业完成时分注管柱力学状态Fig.7 Mechanical condition of layered water injection string

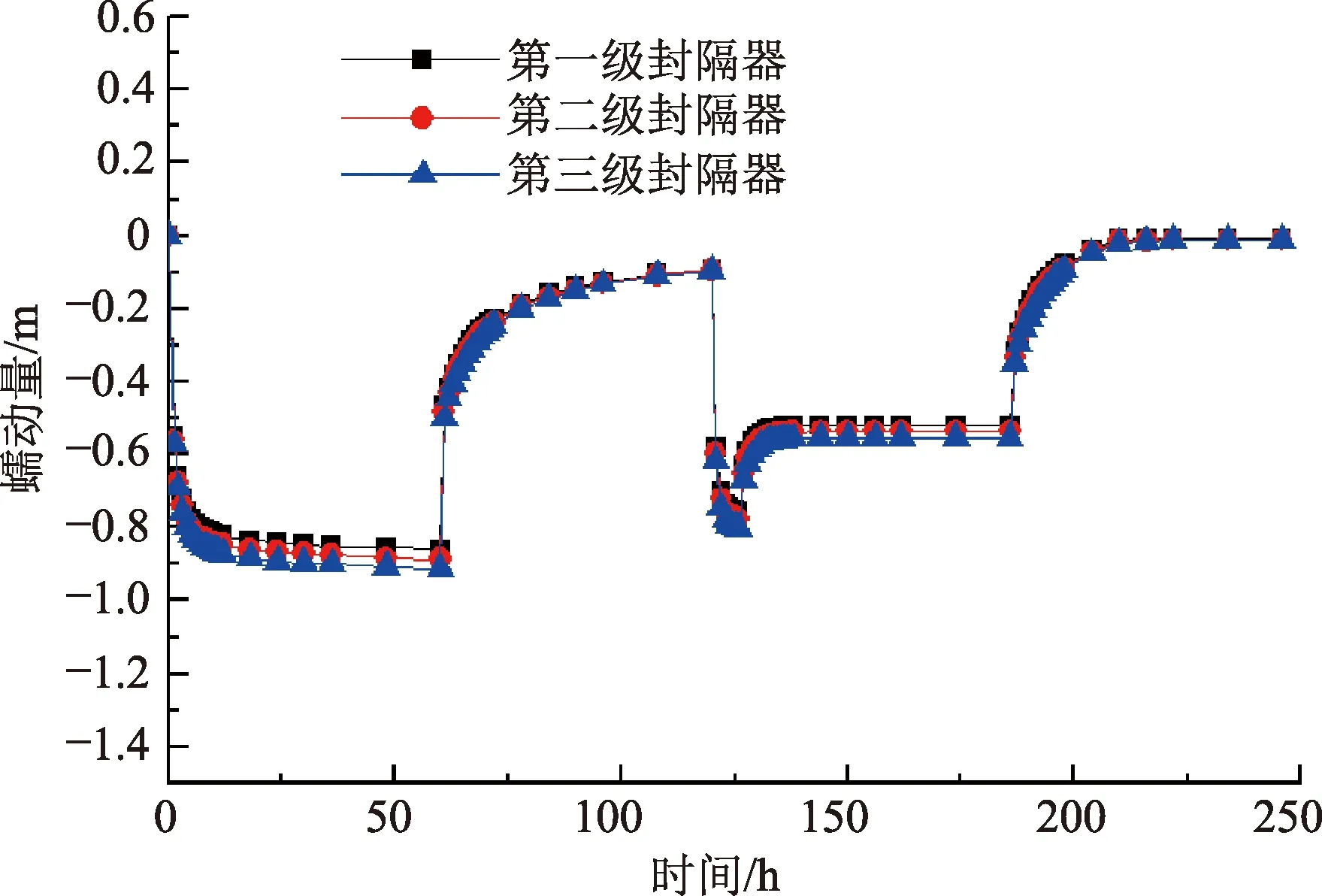
图8 不锚定作业全工况蠕动规律Fig.8 Peristaltic law of water injection condition without anchoring

第一阶段注水作业完成后,利用细分注水算法算得第一级封隔器蠕动量为0.96 m,现场测量得到第一级封隔器处摩擦行程为1.05 m,误差为8.57%。此外,对胜利油田河31-161、史8-更38、HJSH109-X1等20余口实例井进行蠕动量计算,计算结果误差范围为8%～15%,反映出该蠕动算法的可靠性。

若对该井在第一级封隔器上端施加刚性锚定,对注水管柱开展蠕动分析,得到其蠕动规律如图9所示。

图9 顶端锚定作业全工况蠕动规律Fig.9 Peristaltic law of top anchoring water injection condition

在施加锚定的条件下,该注水管柱总体向上收缩蠕动0.288 m,在作业过程中施加锚定可以大幅度减小注水管柱蠕动,注水一定时间后,管柱趋于稳定状态;停注工况转换为洗井工况时,由于水力锚锚爪收回,且洗井排量较大,管柱发生蠕动现象。

由图8和图9对比可得,施加顶部刚性锚定后,注水工况及工况转换全过程中注水管柱蠕动量均大幅减小,为防止管柱蠕动造成封隔器失效,应根据油藏细分开发需求,合理优化注水参数及锚定工艺,提高注水管柱使用可靠性。

4 结 论

(1)轴差力是温度、压力等工况条件变化对位移受限管柱的一种作用表现形式,其作用效果是促使管柱产生位移。注水管柱发生蠕动现象的原因是封隔器处的轴差力大于最大静摩擦力。

(2)不同工况转换过程中,由于温度、压力变化剧烈,管柱蠕动明显;由于轴向力在管柱上的传递,各级封隔器蠕动变化规律随时间变化基本一致。注水管柱施加刚性锚定后,各级封隔器蠕动量均大幅减小,应根据油藏开发需求,合理优化注水参数及锚定工艺。