基于水动力学理论的上游水电站围堰漫顶水位变化模型

李晓光

(中国水利水电第十一工程局有限公司，郑州 450000)

0 引 言

围堰是修建的临时性坝工，主要为了水利枢纽建筑物能在干地上进行施工和检修，工作条件比较特殊[1-2]。在水利枢纽工程中，围堰的布局和施工程序对工程的整体进度和工程质量有重要影响，对工程施工格局起到决定性作用，甚至涉及下游的安全问题[3]。

影响围堰实际效果的主要因素是水位变化，若上游水电站围堰遭遇超标洪水发生漫顶溃决，将严重影响中下游水电站施工的安全。面对这种情况，有研究者提出上游水电站围堰漫顶水位变化模型。据国内外大量统计资料显示，在失事的大坝中有近50%是由于渗透破坏引起的。在以往的研究中多数考虑渗透破坏的问题，研究较多、使用范围较广的有基于Autobank的水位变化模型和基于数值模拟的水位变化模型[4-6]。在上述两种模型中，由于模型参数的取值为特定的范围，在实际应用中无法取最优值，导致水位变化模型对水位变化的响应程度较差，拟合优度异常且对水位的敏感度低[7]。针对这种情况，设计基于水动力学理论的上游水电站围堰漫顶水位变化模型，水动力学理论主要研究水与其它液体的运动规律及其边界相互作用，利用这一理论，解决以上使用的模型中存在的问题。

1 基于水动力学理论的上游水电站围堰漫顶水位变化模型设计

1.1 基于水动力学理论确定模型参数

在研究中模拟上游水电站围堰漫顶水位变化情况，控制进出水位以扩散流动为主，节省模型执行时间[8]。模型设计中设置时间步长时，使收敛值小于1，使模型在显示格式的条件下，计算过程始终保持稳定。在水位变化模型计算中，上游水电站围堰漫顶水位变化区域划分为多个单元网格，为了检测网格更为方便，设置网格点的收敛值与时间步长相同，均小于1。检测中使用的时间步长取浮动取值范围，设置一个最大时间步长，一个最小时间步长。在水位变化模型实际应用中，分别设置收敛值为0.08，最小时间步长为0.002，最大时间步长为5 000。在模型计算过程中，根据扩散方程的时间步长确定检测水体的时间步长[9]。

将上游水电站围堰漫顶水位变化区域划分为多个单元网格，将网格点按照检测的水深分为干点、半干湿点和湿点，每个网格单元的临边利用上述中设置的时间步长确定，待所有网格检测完成后，获得整个区域的水体边界位置。

根据网格水深分类的条件如下：正常情况下网格的水深为静水深，网格干水深大于一边水深，淹没水深远小于另一边水深，此时，小于水深的静水深网格与另一网格的表面高程之和大于零；模型设计中，设置干水深为0.005 m，湿水深为0.1 m，半干湿点水深为0.05 m。在模型设计中，只有网格水深小于干水深，才能参与模型中的计算；如果某一网格的水深介于干水深和湿水深之间，则在模型设计中只计算该网格的质量通量，将动量通量设定为零；最后对于判定为湿点的网格，在模型计算时，将网格的质量通量和动量通量包含在内，此时该点网格满足水体水深大于湿水深[10]。

水动力学理论也被称为流体动力学，在流体动力学中，水体的运动会产生雷诺附加应力，受到网格尺度的影响，当雷诺附加应力施加在时间上产生“涡黏”[11]。因此，考虑涡黏系数对模型的影响，将其拆解为平均值，设置为常数，经过梯度化处理后减小雷诺附加应力对模型造成的影响。围堰边壁的粗糙程度直接影响水流的运动情况，糙率是水位变化模型主要参数之一，利用土地利用图参考粗率表分析围堰区域底部和边壁的粗糙程度，提取出曼宁系数图，确定围堰区域底部和边壁的糙率。在糙率的确定过程中，利用时间步长检测到水体流速值，将其与模拟的流速值对比，观察两者的吻合情况。曼宁系数合理时，模拟流速值与实际流速值吻合程度良好；反之，吻合程度差，说明曼宁系数不能满足模型实际需求，模拟水位值与实测水位值之间存在较大误差。对于这种情况，重新取值，直到误差控制在正常范围内。

水位变化与降水蒸发、水体密度相关，考虑上游水电站的地点，结合当地气候气象的条件，设定降雨蒸发参数，当地的降水量和蒸发量的数据可在气象网站上下载[12]。假设在水位变化模型中，基于标准海水方程，确定水体密度温度和盐度，使温度范围和盐度范围控制在符合模型需求的范围内[13]。

在模型设计中，模型执行时水体密度保持不变。至此，上游水电站围堰漫顶水位变化模型参数设置完成。

1.2 建立水体动量方程

水体动量方程在直角坐标系的条件下建立，水位变化连续方程如下：

(1)

式中：z为水位；x为距离；t为时间；ρ为水体密度；a、b、c分别为X、Y和Z方向的流速分量。

则X方向的水体动量控制方程为：

(2)

Y方向的水体动量控制方程为：

(3)

Z方向的水体动量控制方程为：

(4)

基于以上公式，确定湍流动能控制方程、湍流耗散控制方程以及湍流能产生项[14]。湍流动能控制方程：

(5)

湍流耗散控制方程：

(6)

湍流能产生项：

(7)

式中：ζ为有效黏性系数。计算公式为：

(8)

式中：F为湍流常数；M为湍动能产生项；σ为湍流动能耗散率；α为湍流动能[15]。

则三维直角坐标系下的水体动量控制通用方程为：

(9)

通过以上过程完成水体动量方程的建立，基于此方程，计算上游水电站围堰漫顶水流，完成水位变化模型的设计。

1.3 计算围堰漫顶水流

将上游水电站围堰看作单元，由单元网格组成，根据模型参数将单元网格划分为若干个计算断面，在计算断面前对水体动量控制方程进行有限差分运算，得到以水位和流量为变量的方程组，得到上游水电站中各个网格水位。将得到的结果回代至单元中，最终得到整体的水位和流量，完成上游水电站围堰漫顶水位变化模型的设计。

计算时，从末尾网格向首位网格推导，令：

ΔRi+1=βi+1+χi+1Δzi+1+ηi+1Δzl1

(10)

式中：Δzi+1为第i+1个断面在Δt时间内的水位增量；ΔRi+1为第i+1个断面在Δt时间内的流量增量；β、χ、η为断面系数，其中β为常规系数，χ为Δzi+1的断面系数，η为zl1在Δt时间的断面系数，zl1右下角表示断面。

对式(10)进行线性化处理，得到：

βi+1ΔRi+χi+1Δzi+ηi+1(ΔRi+1)=φ1

(11)

βiΔRi+1+χiΔzi+1+ηi(ΔRi+1)=φ2

(12)

联立式(11)和式(12)，消除Δzi+1，得到系数βi、χi和ηi，对于同一断面的流量有：

ΔRi=βi+χiΔzi+ηiΔzl1

(13)

首末断面关系设有如下的线性方程组：

(14)

流量边界条件以下列形式给出：

(15)

水位边界条件以下列形式给出：

(16)

式中：Ji和Si为边界条件，其中Ji为上游流量边界，Si为下游水位边界条件。

根据能量守恒条件，连接端点的各个网格的水位增量和断面的水位增量相同，则通过式(13)、式(14)和式(15)即可求出各个网格每个断面的水位与流量。至此，设计的基于水动力学理论的上游水电站水位变化模型设计完成。

2 上游水电站围堰漫顶水位变化模型实验研究

2.1 实验准备

在上游水电站围堰漫顶水位变化模型的实验研究中，引用传统的基于Autobank的水位变化模型和基于数值模拟的水位变化模型，设计对比实验，考虑模型中的通用指标，以水位的拟合结果和模型整体的敏感性作为实验衡量指标，对比不同的上游水电站围堰漫顶水位变化模型的实际性能。

在实验中，以某上游水电站为例，水电站附近的水下地形见图1。

图1 实验区域地形图(高程单位：m)

对应的实验区域的网格见图2。在水电站围堰附近，进行网格的加密来适应水位变化。

图2 实验区域计算网格图

从图2中可以看出，生成的网格接近正交，有助于提高实验精度。在图2中显示的实验区域内，使用不同的上游水电站围堰漫顶水位变化模型仿真出水位变化，在相同的水淹天数下，获得平均水位的拟合结果，同时获得水位变化量引起的边界流量和渗透系数，计算不同模型的敏感性，依据实验结果分析对比模型。

2.2 平均水位拟合实验结果及分析

设置平均水位的置信带为95%，根据拟合曲线计算出各个模型的拟合优度。平均水位拟合结果见图3。

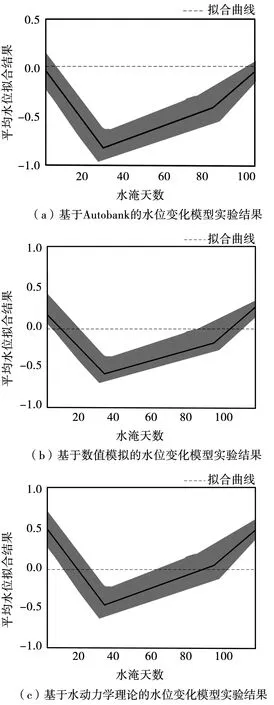
图3 不同水位变化模型平均水位拟合实验结果

图3中显示的深色区域为置信度。从图3中可以看出，只有基于水动力学理论的模型平均水位拟合实验结果中拟合曲线在置信区域范围内，其余实验结果拟合曲线与置信区域存在一定偏差。根据图3中结果计算不同模型的拟合优度，分别为1.647、1.462和1.013。拟合优度是指对观察值的拟合程度，其值越接近1，说明拟合程度越好。从拟合优度计算结果可知，基于水动力学理论的上游水电站围堰漫顶水位变化模型拟合程度更好。通过上述过程获得模型的敏感性参数，分析不同模型。

2.3 模型敏感性实验结果及分析

通过上述获得敏感性相关参数，3种不同模型的参数见表1。

表1 模型敏感性参数结果

表1中两个参数对水位变化的影响存在差异性，通过各个参数的测量值来比较各个模型的敏感性。敏感度计算公式如下：

(17)

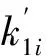
利用上述公式计算得到各个模型的敏感度分别为3.237、4.674和7.437，模型的敏感度越高，说明模型能够更好地反映上游水电站围堰漫顶水位变化。结合平均水位拟合结果和模型敏感性可知，设计的基于水动力学理论的上游式电站围堰漫顶水位变化模型拟合程度更好，且敏感性更高，说明该模型对上游水电站围堰漫顶水位变化的响应程度更好。

3 结 语

本文围绕上游水电站围堰漫顶的水位变化情况，在原有水位变化模型的基础上，研究基于水动力学理论的上游水电站围堰漫顶水位变化模型。针对原有的水位变化模型中存在的响应程度差的问题，设计对比实验，验证水位变化模型设计中应用水动力学理论，有效地解决了原有的水位变化模型中参数不能达到最优取值、导致模型响应程度差的问题。但设计过程中依然存在一些问题。受环境条件的限制，在上述研究过程中主要以小流域为目标，在后续研究中希望考虑大流域，另外模型的实际应用还需要考虑经济成本问题，综合分析与研究目标相关的各项经济影响因素，使模型具有较高的性价比。