基于MPCR 的TE 质量相关故障检测

张爱华，吕承聪，高闻孝

（渤海大学工学院，辽宁锦州121013）

0 引言

随着科技的进步和发展，大规模机械化生产已经到来，自动化机械系统随着智能化的发展也变得越来越复杂.因此，机械正常稳定的运行十分重要，一旦发生故障所带来的后果则是不可估量的.例如：2019年3月埃塞俄比亚的客机波音737-MAX8型，由于无法操纵飞机，飞机自动俯冲造成坠机，客机上所有的人都没能逃脱；2005年11月吉林市双苯厂由于其P-102塔发生堵塞循环不畅导致了爆炸，造成经济损失的同时也带来了巨大的污染；2019年3月江苏中丹化工技术有限公司污水车间废水储罐发生火灾事故，在带来经济损失的同时，更重要的是导致生命的消逝.因此，对工业系统进行性能的监控，有效的防止各类故障所带来的危害至关重要的.在过去的几十年中，诸多研究者对此进行了深入的研究，并提出了可行的解决办法，例如，基于解析模型的非系统性的性能监控方法受到广泛地关注，并且广泛地应用于航天器以及机器人等相关领域中［1-3］.但由于现在工业系统构造和原理的复杂性日益增强，特别是化工相关的生产系统，导致难以在短期内建立精准的模型.随着计算机和传感器的迅速发展，系统在运行时很多相关的数据会被采集到，使得基于数据驱动的故障检测技术受到研究者的关注，并成功的广泛应用于过程监测中，例如在化工、冶金、医药等领域［4-9］.

基于数据驱动的方法中包括机器学习、信号处理、多元统计等方法.其中多元统计方法由于依托统计学的知识，对系统无需了解过多的先验性知识和精准的模型，而受到研究者的关注并将其应用于复杂系统中［10-14］.基于多元统计的数据驱动方法主要理论涉及主元分析（Principle component analysis，PCA）、偏最小二乘（Partial least squares，PLS）等［15］.PCA算法在降低维度的同时，也因此简化了故障的检测.但是只要PCA检测到系统发生变化就会立即报警，会产生过度敏感的问题.然而在现实情况中，有些过程变量的变化并不会引起产品质量的改变，但这种与质量无关变量变化所引起的故障，仍然会指示系统故障发生的报警.这种误报警会迫使庞大的工业系统停止生产，进行检修.这样不仅增加了检修的费用，同时停产也会带来损失.虽然研究者也发现了此问题，并进行了基于质量变量和过程变量的故障诊断方法研究，主要涉及多元线性回归（Multiple linear regression，MLR）［16-17］、PLS［17，18］、规范变量分析（Canonical variable analysis，CVA）［19，20］、主元回归分析（Principle component regression，PCR）［21-24］等.其中文献［18］所提出的改进PLS方法就可以用来处理质量相关故障问题，文献［22］IPCR是在PLS的基础上更彻底的分解过程变量X，使得检测更准确.

本文所提出的MPCR可以在排除一些与质量不相关的变量后，进行基于数据的建模.该方法在降低了检测数据维度的同时，也简化了对工业系统故障的检测方式.在TEP故障检测中，利用其普遍存在两个变量作为质量相关变量，具体变量的选取在TEP仿真中有详细介绍.在此之上，将两次检测得到的T2取均值用来判断是否有故障发生.为了验证所提出的算法的有效性，采用IPCR和PCA在TEP过程中进行性能的检测的对比.可以看到在TEP的故障5和故障7中，所提出来的MPCR效果明显的好，同时，对于其他类故障也有较好的检测结果.实验证明相比单一的质量相关变量而言，两个质量相关变量能更好的实现工业系统性能的监测，并且本文所提出的MPCR性能监测方法优于PCA、IPCR.

1 IPCR

针对之前一些传统算法不能建立起质量变量与过程变量之间的关系，以及由此所导致的无论是否两变量质量相关，只要有故障发生，哪怕是不影响工业系统的正常运行与生产，检测系统都会报警，从而会带来不必要的经济损失.因此，有研究者提出基于PCR的相关故障的检测，有效的解决无关故障所带来的误报警问题.随着系统的复杂度增加，有研究者提出了修正PCR性能检测方法，如文献［22］提出了IPCR，从其大量的仿真结果来看IPCR有着较好的检测结果.根据定义算法中涉及的输入变量和质量变量，即输入变量由X=[x1，…，xN]T RN×m表示，输出变量由来Y=[y1，…，yN]T RN×l表示，则IPCR的算法如下.

首先，根据的PCR算法得到质量变量之间的系数矩阵M，具体过程可以参考文献［22］.

其中X和˜分别代表变量的主元部分和残差部分并且彼此互相正交.

其次，对MMT进行奇异分解，可以得到如下结果

其中X表示其与Y高度的相关˜表示其与Y高度的不相关.Tre代表X的得分矩阵，Tun表示˜的得分矩阵.在线检测时，IPCR将样本同样分解成两部分，然后由式（5-6）得到tre和tun.

由此可以确定X和˜的T2统计量

若置信限设置为α，则的阈值为

其中（Fm,N-m,α）表示自由度为m和N m的F分布.

最后，根据阈值式（15-16）来判断发生故障的类型，详细算法过程如下：

2 互信息

互信息描述的是一个随机变量中包含的关于另一个随机变量的信息量.它不仅限于简单的线性关系，而且可以用来评价两个随机变量之间的非线性相关程度.两个变量之间的相关性越强，相互信息的值越大.若两个变量相互独立，那么互信息值为0.因此，系统性能监测或故障诊断中可选用互信息来筛选出与质量更相关的过程变量.其公式如下

其中p（x）和p（y）分别是X和Y的边缘概率分布函数，而p（x，y）为X和Y的联合概率分布函数.然而在实际计算过程中，概率密度函数通常难以计算，因此，互信息采用

计算获取.其中H（x）和H（y）是边缘熵，H（x，y）是联合熵.H（x）、H（y）、H（x，y）可由

确定.此外，特别需要说明的是对于取得前K个变量要满足

其中n为备选x的个数，k为选出变量的个数.

3 MPCR

基于PCR的IPCR算法很好的构造了质量变量与过程变量之间的关系，整体上也能表达系统总体状况，但其仍存在一定的缺陷，例如在无关故障中报警率过大，以及不能及时反映系统真实情况等.本文针对不足的问题提出了MPCR对其改进，具体对不足的改进与效果将在TEP仿真实验中详细的进行分析与论证.MPCR方法，首先要对样本输入到IPCR模型之前采用互信息对其进行筛选处理，依据式（22）剔除不需要的变量；其次将过程变量与两个质量变量分别建模，并取得所有统计量的均值；最后，在通过阈值式（15）判断，实现系统故障的精确诊断.具体的算法步骤如下.

步骤1对X与Y进行标准化处理；

步骤2对X和Y1与Y2进行互信息运算选出与Y相关程度较大的X；

步骤3将选出的X与Y1代入到IPCR模型根据式（5）得到Tre1；

步骤4将选出的X与Y2代入到IPCR模型根据式（5）得到Tre2；

在线监测

步骤5由式（15）设置质量相关故障统计量的阈值

步骤6将已选好的在线样本X和Tre1代入式（9-13）中求得；

步骤7将已选好的在线样本X和Tre2代入式（9-13）中求得

步骤8将取均值后得到Tre2；

步骤9若Tre2大于则产生质量相关故障，反之无质量相关故障发生.

为便于描术本文所提出一种修正标准主成分回归的质量相关故障检测方法，此出给出故障检测过程的流程图如图1所示.

4 TEP仿真实验

TEP是由伊斯曼公司提供一个测试平台，它是基于真实的化工过程创建的仿真模型.由于该过程较好的反映出实际复杂工业过程出现的问题，因此，该测试平台被广泛的应用于工业系统的过程性能监控和故障检测与诊断等相关领域中，TEP模型如图2所示［22］.此过程主要有5个生产单元，8种反应成分，其中B是惰性气体.反应过程如下所示

式（23）过程一共有22个测量变量、12个操作变量和19个成分变量，整个过程设置了21个故障，其中故障1-15为已知故障，其中质量相关故障有故障1、2、5、6、7、8、10、12、13，其余为质量无关故障.MPCR中质量变量选择的是成分变量XMEAS（35）和XMEAS（38），原因是诸多文献以及文献［25］的质量变量选择均在上述变量中选择作为质量变量，本文后续仿真实验即利用上述已知故障来进行仿真验证.其中α的取值为0.99，δ取值为0.55，由文献［25］TEP仿真部分可知δ取值略小于0.55效果变化不大，但是略大于0.55效果明显变差，因此，系统测试在选择变量个数时要尽量满足δ取值在小于0.55处向0.55无限接近.综上，过程变量是在测量变量和操作变量共计33个量中选出17个与质量变量相关程度较大的变量.PCA和IPCR的过程变量按文献［22］取33个，α的取值为0.99.实验数据包括故障数据和正常数据，正常数据用于建模，故障数据用来检测，故障数的样本数一共960个，其中前160为正常数据.

由于TEP系统中存在着许多闭环反馈机制，因此，在有些故障发生之后系统会逐渐恢复正常，其中故障5和7就是此类故障.以故障7为例，利用格拉布斯（Grubbs）检验法对两个质量变量进行异常值的分析，其中建模部分所采用的数据是前160个正常的样本，参数g0的取值是按照正常样本无异常来确定的，检测结果如图3和图4所示.图3-4中红线代表阈值，超过阈值则报警.

从图3中可以明显的看出XMEAS（35）在将近400点已经恢复正常，从图4中可以明显的看出XMEAS（38）也在600点左右恢复正常.此外，从图3-4还可见当故障7发生时质量变量发生明显的改变，因此故障7也是质量相关的故障.IPCR对故障7的检测结果由图5可明显的看出在靠近800点左右的两部分有明显的报警，图6中PCA对故障7的检测虽然也有回归的趋势但是仍然一直报警.而图7中MPCR对故障7的检测结果更加符合质量变量的变化的情况，在600多点以后不再报警.可见MPCR在对故障7的检测结果中更加贴近质量变量的变化，因此在故障7中MPCR的检测结果优于IPCR和PCA.

此外在故障5中质量变量也是在400点左右恢复正常的，然而IPCR对质量相关故障5的检测却一直报警，如图8所示，PCA也是断断续续的报警，而MPCR却也能很好的反应系统的真实情况如图10所示.

经过仿真统计在TEP的15个已知故障中检测效果优于IPCR的有故障（2-10、12、15）共计11个，其中无关故障3和相关故障10的效果通过图11-16容易的看出，无关故障MPCR的报警率少，相关故障MPCR的报警率高和理论的趋势相符合，在PCA中无论相关故障10或者无关故障3报警率都比较高，因此MPCR对于故障检测的结果更优越于IPCR.为进一步说明本文所提出的故障检测方法MPCR的有效性，此处增加对余下故障检测结果统计分析，详见表1-2.通过表2质量无关故障的检测率，可以看出MPCR对无关故障的检测率成倍数的小于IPCR的检测率，个别的检测率几乎接近0，而PCA的报警率是非常高的，然而对无关故障的检测的理论值应该为0，进一步证明了MPCR故障检测方法的优越性.

从表1中可知，MPCR对于一些质量相关故障的检测率也高于IPCR的检测率，即使个别质量相关故障的检测率低于IPCR的检测率也做到大部分的报警.虽然大部分PCA的报警率高于MPCR但是在无关检测中PCA对故障的检测率也高于MPCR，说明了PCA对所有故障都比较敏感，正如之前所提到的该方法无法明确的区分质量相关和无关故障，只要发生变化就会产生警报.综上可见本文所提出来的MPCR算法优于PCA和IPCR.

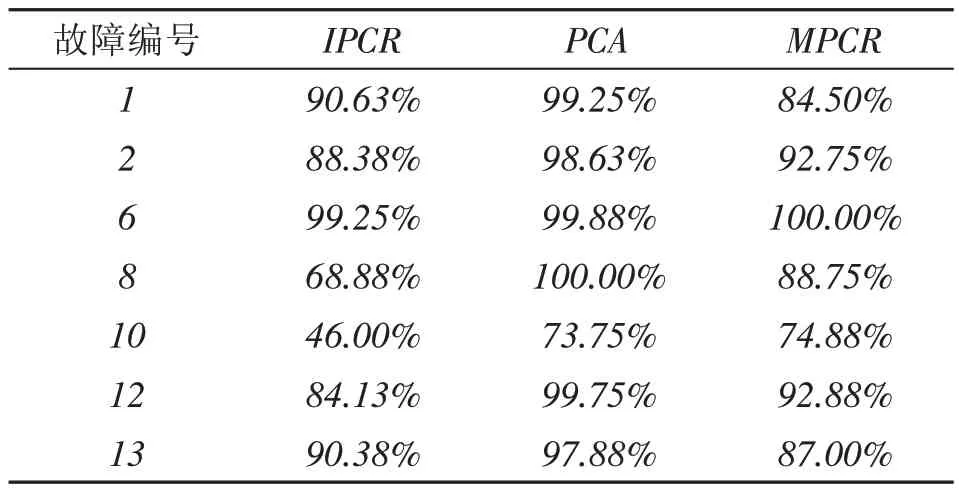
表1 TEP的相关故障的检测率

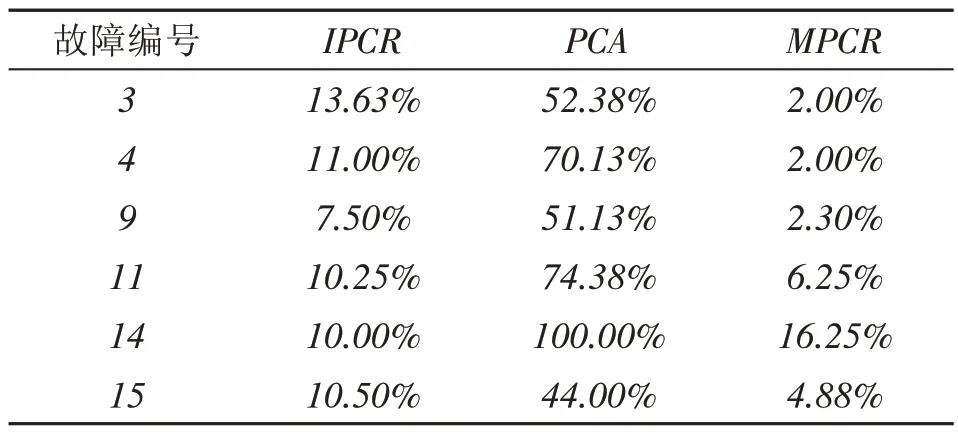
表2 TEP的无关故障的检测率

5 结论

本文提出的MPCR算法，首先利用互信息压缩输入矩阵后又用两个质量变量同时对系统检测，增强了对故障检测的效果，与IPCR和PCA比尤其在TEP具有反馈调节型的故障5和7的检测中能更好的体现出质量变量的变化，即在质量变量回归正常时，MPCR也停止报警，因此MPCR能比较好的用于TEP系统的相关故障检测.