基于卷积神经网络的航标图像同态滤波去雾

陈遵科

(交通运输部 东海航海保障中心厦门航标处， 福建 厦门 361000)

受雾霾影响，某些海上目标(如航标)的特征会变得模糊，导致无法识别，给航行安全带来影响。以厦门港为例，2012年雾天39 d，封航51次，封航306.3 h；2013年雾天29 d，封航37次，封航193.6 h；2014年雾天33 d，封航42次，封航270.2 h；2015年雾天27 d，封航33次，封航182.4 h；2016年雾天29 d，封航33次，封航415.8 h。单次封航时间最短在2012年4月25日，为18 min，最长在2016年2月12日，为2 595 min。因此，有必要研究去雾图像算法，以减小雾天低能见度给航行安全带来的影响。

同态滤波[1]由A.V.Oppenheim和Ronald W.Schafer提出，通过压缩图像的动态范围，在削弱低频分量的同时增加高频分量，提高对比度，锐化图像边缘并保留其细节，实现优质的去雾效果。江玉珍等[2]针对细节信息丢失的医用X光图像，增强反映病理的边缘纹理信息。田小平等[3]引入新传递函数改进同态滤波，通过控制参数t调整滤波效果，减少调参，较快实现滤波。巴特沃斯滤波器在通频带内的频率响应曲线较为平坦，没有纹波，在阻频带逐渐下降为零，广泛应用于语音降噪、加速度传感器信号数据处理、称重和注塑机等领域中。王秋云等[4]通过对照度不均的车牌图像，构造巴特沃斯带阻同态滤波，计算图像频率分量的幅度谱估算截止频率。余成波等[5]对曝光不均、细胞轮廓不清晰的角膜内皮细胞图像进行CLAHE增强之后，再进行同态滤波。王新竹等[6]针对彩色图像亮度不足，将多尺度MSR(Multi-Scale Retinex)算法与同态滤波相结合改进图像效果。

同态滤波属于频域增强，将图像从空域转换到频域，在频域进行高通或低通滤波实现图像增强，再通过逆变换返回到空间域。[7]同态滤波包括高斯型、指数型和巴特沃斯型等。经过指数同态滤波后的去雾图像，局部细节仍有些模糊。经过高斯同态滤波后的图像局部易出现过度增强引起的“白化”，明暗对比强烈之处不够均匀。本文对同态滤波去雾算法进行研究，对比分析3种不同函数的同态滤波对航标图像去雾的效果图，并选择巴特沃斯函数作为同态滤波的传递函数，研究其参数对航标图像去雾的影响。

1 同态滤波图像增强算法

1.1 同态滤波算法原理

同态滤波基于照射-反射模型，利用傅里叶变换将对应反射分量和入射分量的高低频成分分开操作，减少低频成分的同时获得更多的高频成分，增强图像暗区域的细节和对比度，并将运算转换至对数域，提高算法的效率并减少运算时间。[8-10]

Do为滤波器的截止频率，用户通过设定Do的值实现对高频分量的增强和对低频分量的抑制。为使滤波后的图像在提高亮度的同时保持细节的清晰，引进常数c，得到与n阶巴特沃斯高通滤波相对应的同态滤波自适应传递函数[11]为

(1)

式(1)中：c为控制斜面锐化的系数，用于控制输出图像的锐化程度；rl为低频增益；rh为高频增益，且rl1时，图像的低频成分减少、高频成分增强，从而提高对比度；D为该点到图像中心的距离。

1.2 巴特沃斯同态滤波流程

为保证同态滤波的滤波效果，关键在于选择合适的同态滤波的传递函数H(u,v)，通常其传递函数有高斯型、巴特沃斯型和指数型等3种类型。[12]本文主要基于同态滤波对航标去雾图像进行研究，通过大量试验发现巴特沃斯型同态滤波对航标图像去雾效果最为明显，因此对巴特沃斯同态滤波去雾图像进行研究。通过进行傅里叶变换，计算频率的原点，设置巴特沃斯同态滤波的截断频率和高低频增益，控制滤波器函数斜面锐化的常数c等方式进行滤波，最终显示滤波后的图像和直方图。

2 不同类型同态滤波的航标图像去雾比较

高斯型同态滤波的计算式为

(2)

经过高斯滤波器的图像过于光滑，易丢失部分细节和边缘信息。

指数型同态滤波的计算式为

(3)

指数同态滤波器具有衰减较快的特性，比相应的巴特沃斯滤波器要稍微模糊一些。

为验证巴特沃斯同态滤波算法对航标图像去雾的适用性，本文选取大量航标带雾图像，将高斯型、巴特沃斯型和指数型同态滤波的航标去雾图像进行对比见图1和图2。

a) 原始图

a) 原始图

由图1和图2可知：经过巴特沃斯同态滤波后的灯塔图像细节保留的最多，且其明暗对比强烈之处过渡比较平滑；经过指数同态滤波后的去雾图像整体效果也较好，但局部灯塔细节仍有点朦胧，例如：图2b灯塔顶端还处于有雾状态，增强效果没有图2c明显；而经过高斯同态滤波后的灯塔图像局部出现过度增强引起的“白化”，明暗对比强烈的地方处理得不够均匀；图2d灯塔顶端去雾效果也不明显。

仿真试验结果表明：巴特沃斯同态滤波更好地保留图像的细节，且通过压缩图像的动态范围，校正光照不均的图像的亮度，使图像中原本明暗对比强烈的部分趋于平滑，优化去雾效果。

3 巴特沃斯同态滤波参数研究

图像的频域滤波可理解为

1) 先对f(x,y)图像进行傅里叶变换，将图像从空间域转换至频域。

2) 在频率域用滤波函数H(u,v)进行一系列滤波操作。

3) 通过傅里叶逆变换得到滤波后的图像g(x,y)。[13]整个流程见图3。

图3 滤波操作流程

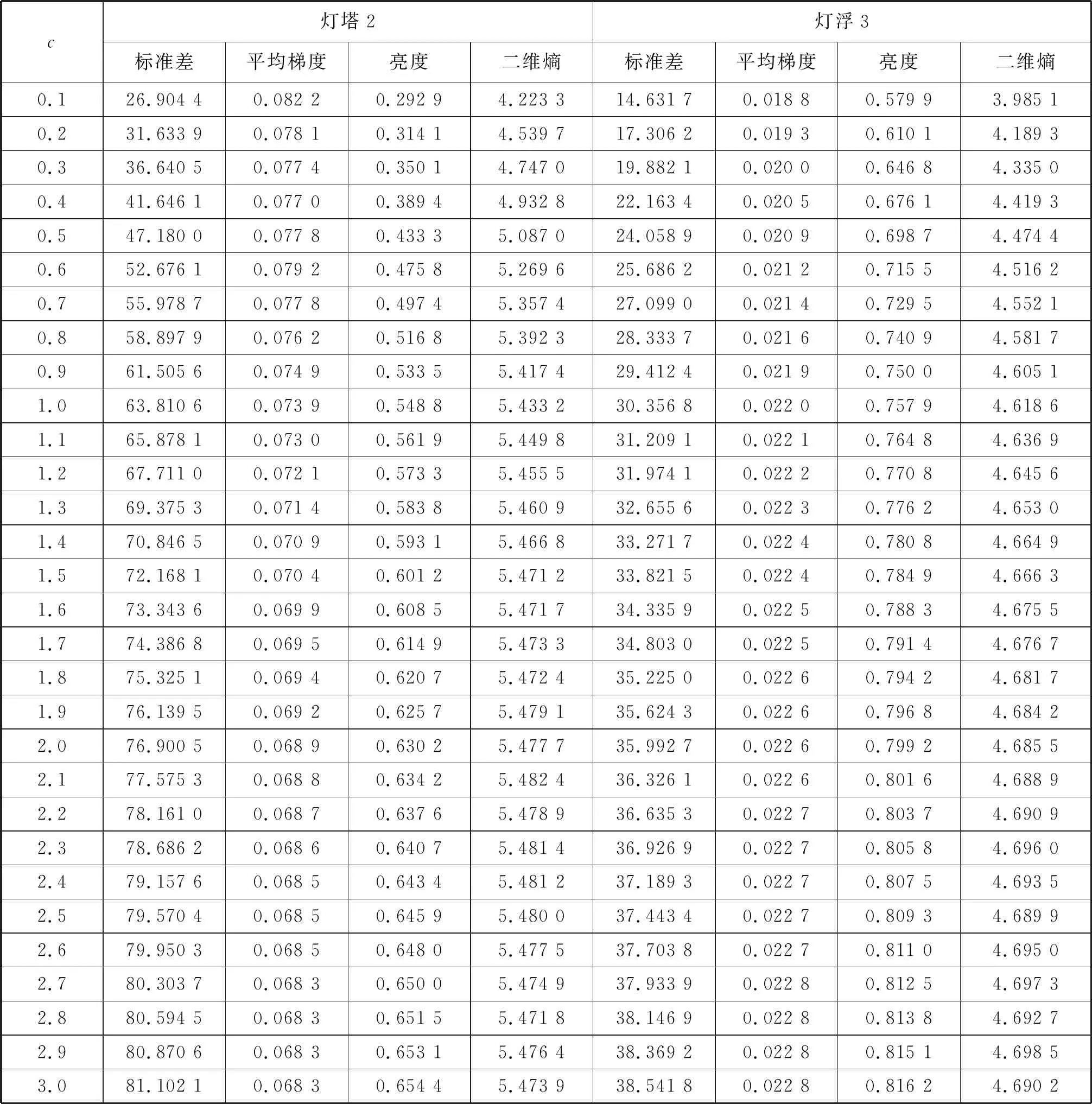
对滤波传递函数中的参数c进行理论分析。由于同态滤波的传递函数一般是基于高通滤波函数构造的，因此，丢失许多低频成分信息，平滑区域也随之消失，需通过加强高频滤波弥补丢失的信息。因此，在滤波传递函数H(u,v)中添加参数c(rl

3.1 主观评价对比

分别选取c=0.1、c=1.0和c=2.0时的实际数据，验证参数c对航标去雾图像对比度和亮度的影响，结果见图4。

a) c=0.1

由灯塔1和灯浮3取不同参数c的巴特沃斯同态滤波去雾效果可知：若c过小，则亮度过低；若c过大，则远处山峰的轮廓看不清楚，对微小细节反差的表达能力变差。

3.2 客观评价对比

方差是指图像像素灰度值相对于均值的离散程度。方差越大表明图像中灰度级分别越分散，图像质量越好；平均梯度可敏感地反映图像对微小细节反差的表达能力,结果见图5。图像中某一个方向的灰度级变化率大，则其梯度也大。用平均梯度值衡量图像的清晰度，能反映出图像中微小细节的反差和纹理变换特征：该值越大，图像层次越多，图像就越清晰，可评价融合结果图像的细节表达能力；图像二维熵在反映图像包含的信息量的前提下，突出反映图像中像素位置灰度信息和像素邻域内灰度分布的综合特征：图像的熵越大,图像包含的像素灰度越丰富,灰度分布越均匀,图像的地物目标越多,图像的信息量越大,反之则相反；图像亮度即图像矩阵的平均值，数值越大图像越亮。亮度公式[14]为

(4)

a) 原始图

图像对比度即图像矩阵的均方差。其值越大图像的黑白反差度越明显。对比度[15]为

(5)

不同c值对应的图像质量指标见表1。

由表1可知：随着c增加，去雾后图像的标准差、亮度和二维熵相应增加，但平均梯度降低。这说明随着c的增加，亮度增加、灰度级别分散和信息量增大，但对微小细节反差的表达能力变差。例如：当c=0.1时，亮度=80.22,对比度=28.09；当c=1.0时，亮度=191.33,对比度=42.47；当c=2.0时，亮度=249.80,对比度=8.71。图像的灰度级的范围是0～255，越靠近0，图像越暗，越靠近255，图像越亮，因此:当c=0.1时，图像最暗，对比度一般；当c=2.0时，亮度接近255，图像过亮，对比度较差；当c=1.0时，图像亮度居中，对比度也居中，此时图像的增强效果最好。

表1 不同c值对应的图像质量指标

3.3 基于卷积神经网络的同态滤波参数调优

参数c与照度分量和反射分量有关，选择比较困难，需通过反复实践才能确定合适的值。本文通过卷积神经网络训练确定同态滤波器最优参数，选取公开数据集ISCAS 2012 DATA作为卷积神经网络的训练数据。[16]训练数据集样本见图6。

图6 ISCAS 2012数据集样本

卷积神经网络的输入为ISCAS 2012数据集中的含雾原始图，输出为经过计算得到的使采用同态滤波去雾后的图像与GroundTruth图像的峰值信噪比Peak Signal to Noise Ratio, PSNR最大的控制斜面锐化系数c。经过多次训练，得到计算最优参数c的卷积神经网络权重。此时对训练好权值的卷积神经网络输入含雾的航标图，就可得到对应的最优c值。对于灯浮3，最优c值为1.1如表1所示。

4 结束语

本文将改进的巴特沃斯作为同态滤波的传递函数，验证巴特沃斯同态滤波对航标图像去雾的适用性；滤波过程中c与照度分量和反射分量有关，选择比较困难，需通过反复实践确定合适的值；通过卷积神经网络训练确定同态滤波器最优参数c值。卷积神经网络的训练方法今后仍可继续优化，自适应调整传递函数的参数值，得到参数的最优值。