排放限制政策下的中国至东南亚航线散货船调度

马向阳， 卢柄宜， 孙 卓

(大连海事大学 交通运输工程学院， 辽宁 大连 116026)

随着全球气候变化的日益明显，船舶排放问题越来越受到航运界的关注。一直以来，海运巨大的运力造成大量的温室气体和有害气体排放。据统计，海运产生的CO2排放量占世界人为产生的CO2总量的2.2%；其他有害气体(主要为SOx、NOx)的排放量也占世界人为排放总量的3.5%。[1]仅2014年海运燃油消耗量就达2.79亿～4.00亿t[2]，若不及时采取措施，到2050年其温室气体和有害气体的排放量将进一步扩大至当前1.5～2.5倍。[3]

在有关温室气体排放的船舶调度研究中，KONTOVAS[4]在船舶路径选择问题(Ship Routing Problem,SRP)问题的基础上提出(Green Ship Routing and Scheduling Problem,GSRSP)模型并阐述在考虑船舶低碳问题时嵌入速度优化的必要性。DULEBENETS[5]对绿色船舶调度问题提出一种考虑CO2排放成本的混合整数非线性数学模型。WANG等[6]在研究碳排放问题时,引入不同的碳税机制，设计各类机制下的航速模型。除此之外，WEN等[7]、WANG等[8]、NORLUND等[9-10]的相关研究，也将碳排放成本和船舶航速选择、航线规划联系在一起，结果表明：在考虑碳排放成本的前提下,可通过航速优化的手段减少环保成本。

对有关船舶排放控制区(Emission Control Area, ECA)内船舶调度的研究，国内外学者也做了大量的研究，例如:BRYNOLF等[11]提出航运公司可采用3种方式穿越ECA，即转换燃油种类、加装尾气清洁设备和全程使用液化天然气(Liquefied Natural Gas, LNG);FAGERHOLT等[12]将光的折射原理引入船舶行驶中，描述船舶穿越ECA边界的临界点；DULEBENETS[13]研究在严格货物运输时间下，班轮穿越ECA的问题;DOUDNIKOFF等[14]针对ECA内船舶航速、排放和成本等进行数理统计，证明船舶运营成本对ECA内船舶数量有较强的敏感性。此外，国内的部分学者重点研究排放限制政策对船舶航速造成的影响，如唐磊等[15]、陈俊军等[16]和陈映秋等[17]。总结上述研究可发现，排放成本与排放限制政策相互作用，对船舶调度以及航速优化产生重要影响。在绿色航运蓬勃发展的背景下，本文考虑碳排放成本以及ECA扩大对我国东南亚航线经营者收益的影响，以经营“中国—东南亚”航线的船队为研究对象,建立非线性的混合整数规划模型，对东南亚航线散货船队调度进行分析，研究在新一轮航运排放限制政策下航运企业的发展方向。

1 排放政策限制下的调度模型

1.1 模型描述

2018年6月交通运输部办公厅下发《船舶排放控制区调整方案(征求意见稿)》(简称《ECA调整方案》)，其要求将ECA扩大至沿海12 n mile以及内河区域，并自2019年1月1日起，船舶在沿海控制区内航行和靠岸停泊均应使用硫含量不超过0.5% m/m的船用燃油。自2020年起除上述规定外，《ECA调整方案》还要求在靠泊和在海南水域航行时,应使用硫含量≤0.1% m/m的燃油。

因此，“中国—东南亚”航线的散货船承运商不得不综合考虑ECA区域和碳排放限制对航次成本的影响，采取进一步措施优化船队航线和经济航速。

ECA区域对不定期船舶调度的影响见图1，由于船舶在ECA内需采用高价的低硫燃油，促使船舶在ECA区域内行驶时会尽量减少载货量并减速航行。

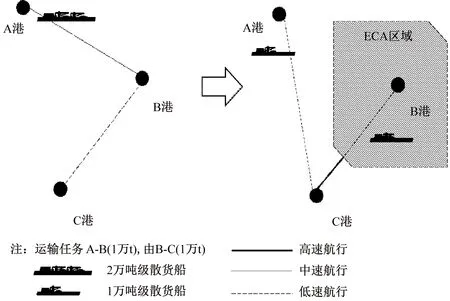
图1 ECA区域对沿线不定期船舶运输影响示意图

由于船舶脱硫改造成本过高，大量船舶采取临时增设双动力燃油舱的方式，在ECA区域外继续使用含硫量较高但价格便宜的动力燃油(Heavy Fuel Oil,HFO)，在ECA内则使用价格较贵的低硫油(Marine Gas Oil,MGO)。在船舶运输过程中燃油消耗主要来自于航行过程中主机燃油的消耗(见图2)，鉴于辅机燃油消耗较小，在相关研究中一般被忽略。模型构建的基本假设如下：

1) 不考虑辅机燃油或岸电成本和船舶在港期间的主机燃油消耗。

2) 不考虑滞港费和速遣费，并保证包运货物按时按量运输。

3) 研究对象为单一船型，但可携带2种类型燃油(HFO和MGO，MGO满足ECA区域内有害和温室气体的排放要求，且在ECA区域内被强制要求使用)。

4) 燃油消耗量仅与排水量和航速有关，不考虑天气或船体情况的影响。

5) 港口使费按船舶总吨计算。

6) 碳税的计算不在ECA内设置排放量阈值，并根据碳排放累计量征收碳税。[18]

马克思对黑格尔唯心主义法学观的批判，解释了法的本质和内涵。 他跳到“私人利益决定法”的命题之外，把握市民社会决定法的深刻含义，得出了财产关系决定法的基本结论，为历史唯物主义法学观奠定了基础。 后来，葛兰西、哈贝马斯等人分别从文化视角和社会公共领域丰富和发展了马克思的市民社会理论，并赋予其新的内容。

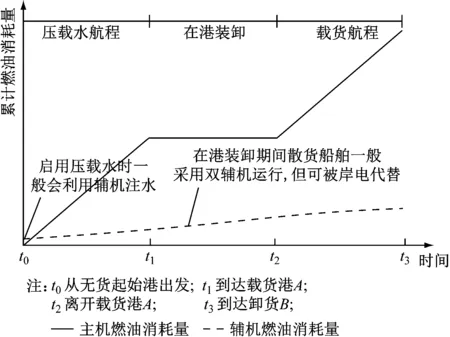
图2 船舶油耗示意

1.2 模型建立

1.2.1船舶燃油消耗量的计算

根据假设，主要考虑船舶主机燃油消耗。而船舶主机燃油消耗与主机动力、船舶排水量和航速相关，不同型号的船舶主机满足船舶主机功率与海军部系数的关系为

(1)

式(1)中：φ为海军部系数;P为船舶功率;Δ为排水量;v为当前航速。

船舶每小时的燃油消耗可表示为

Q′=10-6qeP

(2)

式(2)中：ne为船舶主机燃油消耗率；qe为船舶主机燃油消耗率,g/(kW×h)。

船舶主机航行过程中的总燃油消耗量为

(3)

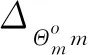
(4)

(5)

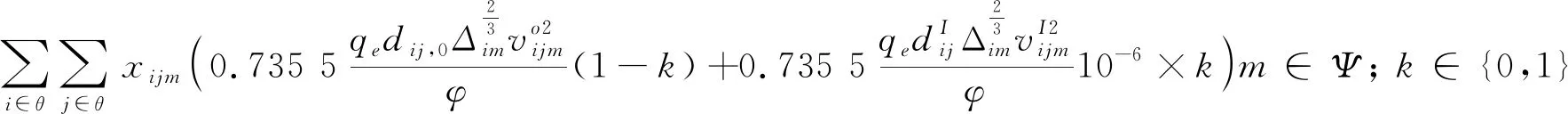
(6)

以最大化船舶承运商利润为目标，式(7)～式(11)分别计算每艘散货船舶的燃油成本Cm1、港口使费Cm2、装卸费用Cm3、固定运营费用Cm4和碳排放成本Cm5；式(12)计算包运合同的运输总成本CT；式(13)为本次调度的最终利润G，目标函数为maxG。

(7)

(8)

(9)

(10)

Cm5=p×Qm×PC,m∈Ψ

(11)

(12)

(13)

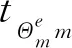
(14)

式(14)为任务分配，即包运合同所列货物必须全被运输。

(15)

式(15)为所有货物都能被运输，即完成一票货物在指定港口间的运输业务。

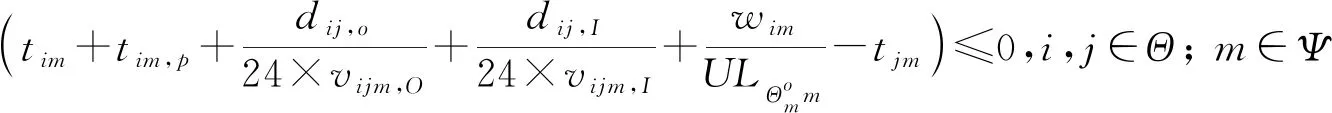
(16)

Tim,min≤tim≤Tim,max,i∈θ1;m∈Ψ

(17)

式(16)和式(17)为时间窗约束，保证m船在i港的离开时间等于船舶在前港离开时间、停泊时间、航行时间、装卸时间和其他在港时间之和。其中:tim为m船到达i港的时间；tim,p为船舶m在港口i的非装卸停留时间(包括引航和停靠泊时间等)；vijm,o和vijm,I分别为m船在从i港到j港段中ECA外和ECA内的航速；ULim为m船在i港口的装卸货速率；Tim,min和Tim,max为允许m船到i港的最早时间和最晚时间。

tim≤t(i+N)m,i∈θ1;m∈Ψ

(18)

式(18)确保船舶在每一个港口先卸货再装货。

xijm(Him+wim-Hjm)=0,i∈θ1;m∈Ψ

(19)

xijm(Him-wim-Hjm)=0,i∈θ1;m∈Ψ

(20)

(21)

Him≤H,i∈θ1;m∈Ψ

(22)

式(19)～式(22)为船舶载货量约束，船舶在i港的装卸货物总额需等于此地的需求额，每艘船舶离港时的实际载货量要小于船舶设计载货量。

vij,min≤vijm≤vij,max,i、j∈θ;i≠j

(23)

式(23)为船舶在航行过程中的速度约束，即船舶在ECA内、外的航行速度应符合该船型理论航速的上、下限。其中:vij,min和vij,max为该船型船舶在i和j航线上航行速度的上限和下限。

(24)

式(24)为每艘船舶应满足既定的起末港口需求。既定的起始港为船舶运输开始时所在的港口，起始港不一定是运输合同中的货运港口；既定的终点港既是货运港口又是船舶最终需要抵达的港口。

(25)

式(25)为船舶出、入港口的一致性，即船舶从i港驶进，作业之后仍从i港驶出。

wim≥0，i∈θ；m∈Ψ

(26)

式(26)为m船在i港装卸的货物数量不为负。

(27)

xijm∈{0,1}，i,j∈θ；m∈Ψ

(28)

式(27)为取消路网中的子回路；式(28)为决策变量xijm，其为0～1整数变量，当xijm=1时为m船承担i港到j港的运输任务。

3 模型求解与案例分析

受ECA和碳税影响的散货船调度模型在求解上有2项困难：

1) 船舶行驶时经济航速的计算，且在穿越ECA时经济航速存在变化。

2) 散货船经常运输大宗货物，存在拆分配送现象。

本文设计的算法解决上述问题,见图3。

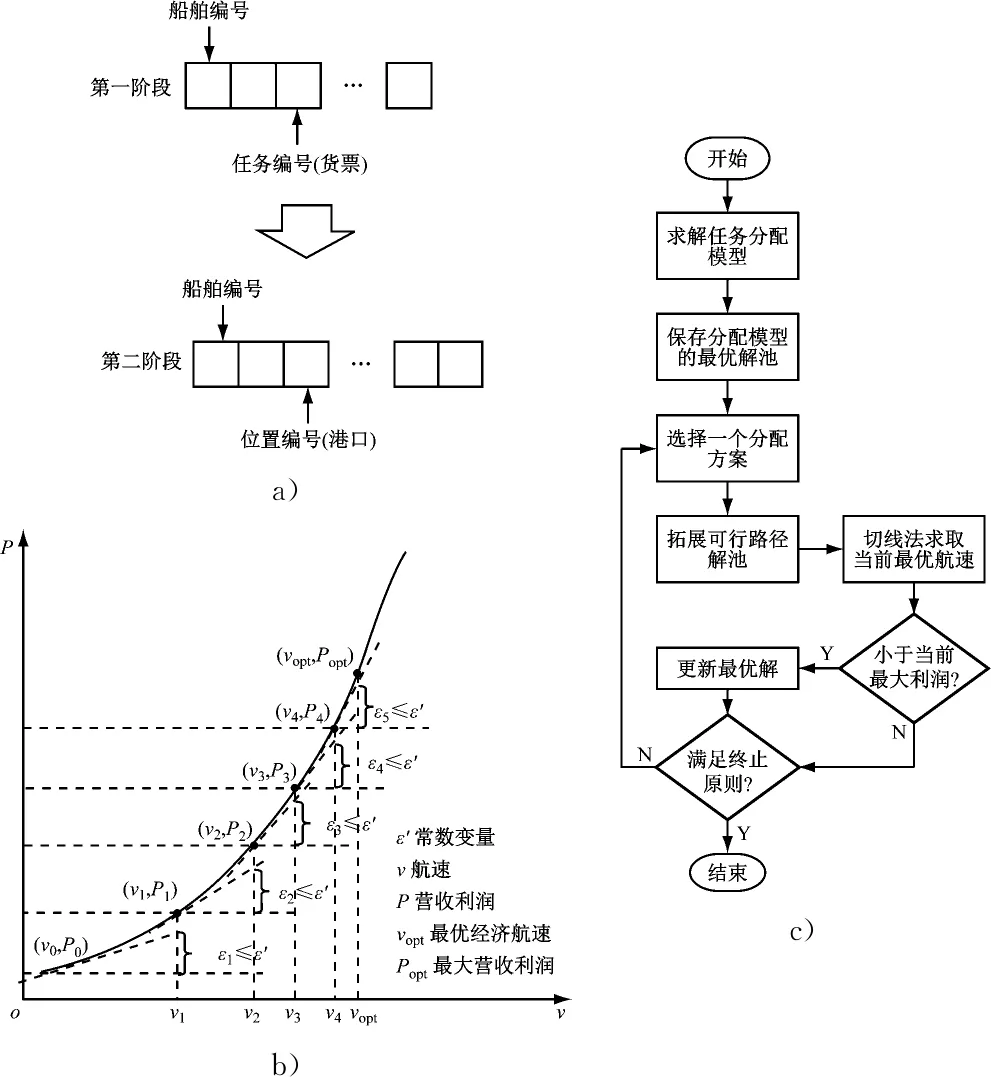
图3 算法示意

(1) 第一阶段仅对运输任务进行分配，对船舶载重和订单总量进行集划分。

(29)

(30)

(31)

式(29)为第一阶段的目标函数,为使用船舶数量最少。式(30)～式(31)为限制每艘船舶在完成运输任务时不超过载重要求。

采用集划分的思想进行求解，求解第一阶段形成以最小船舶艘数完成运输任务的可行解池。

(2) 第二阶段对第一节阶段结果进行编码。如图4a所示：将第一阶段求出的若干可行解拓展成实际航线，再根据船舶调度中时间和速度的相关约束形成混合整数规划模型，遍历可行解池，求解过程中利用图4b的切线法求出船舶在ECA内、外航行时的经济航速，最终判断各可行解的经济价值。当计算规模量较小时，可采取穷举类算法来保障第一阶段的可行解规模，得到精确结论；当计算规模量较大时可采取启发式检索可行解空间。

试验案例船舶信息见表1。HFO为含硫量小于3.5%的动力燃油；MGO为含硫量小于0.1%，均可在我国沿海ECA内航行使用的动力燃油。HFO的价格区间在300～600美元/t，MGO为450～900美元/t。

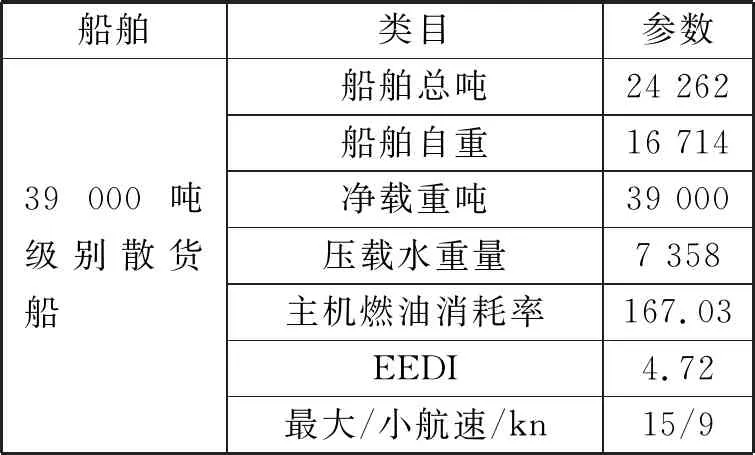
表1 船舶信息表

各港口和航段信息见表2。对该案例进行求解，分析结果见图4，由图4可见：随着MGO和HFO 2种燃油价格的增长，拥有双油舱的散货船显然对MGO价格更加敏感，并且随着燃油价格的不断增长，利润的下降幅度逐渐变大，直到趋于一条直线。进一步分析可得：在国内沿海12 n mile都属于ECA时，船舶在ECA内的航行距离明显增加，导致其对MGO价格更为敏感;船舶在ECA外的航行速度始终受限于在ECA内的航行速度。当航速航线固定时，面对MGO价格的增长，企业会优先提升ECA外的航行速度；当HFO价格增长时，企业只有通过降低航速，延迟交货来避免承担价格上浮带来的大幅度成本上升。例如在当前案例中：当燃油价格开始上浮时，经营东南亚航线的散货船运营商可采用优化船舶调度的方式提升盈利能力;当燃油价格一旦超过某一阈值(算例中为HFO价格超过4 900元/t，MGO价格超过6 900元/t)，运营商将陷入优化困境，难以通过优化船舶速度提升利润，只能承担和上浮价格等比例的上涨成本。

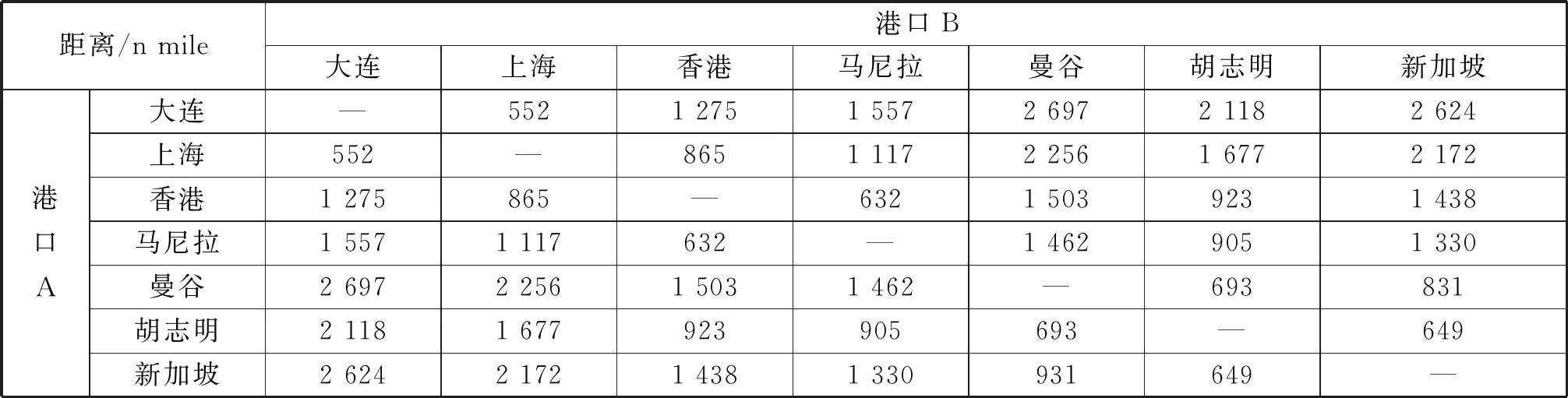
表2 各港口航段信息表

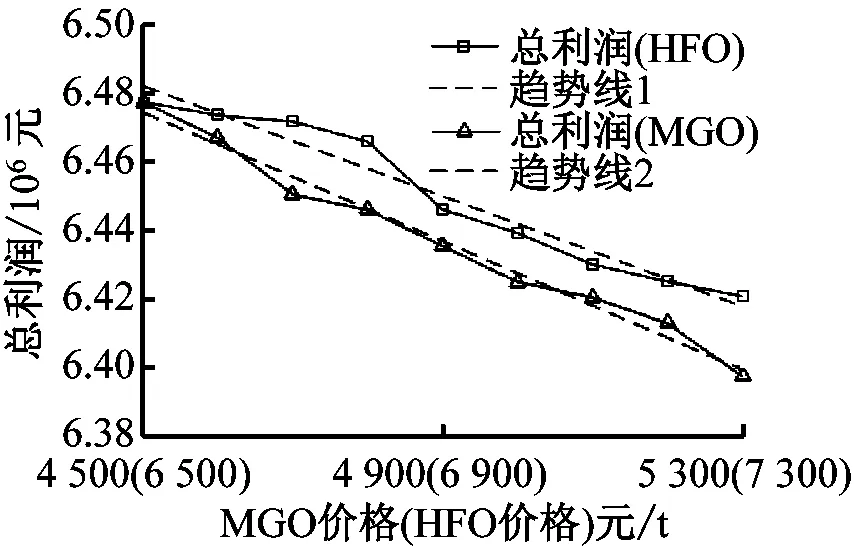
a) N=8， M=5

航速、燃油消耗量和相关成本对比示意见图5。在ECA内、外的航速变化和有、无ECA时，散货承运商的燃油消耗量与燃油成本对比结果显示：随着ECA的扩大和相关排放限制政策的实施，相较于无ECA时，散货船承运商的燃油成本上升15%～30%，整体利润明显下降；而ECA外的平均航行速度明显大于ECA内的平均航速。由于碳税成本占总的燃油成本比例较小，企业呈现出为减少低硫油的使用，加快ECA外航速，因而导致碳的总排放量呈上升的现象。

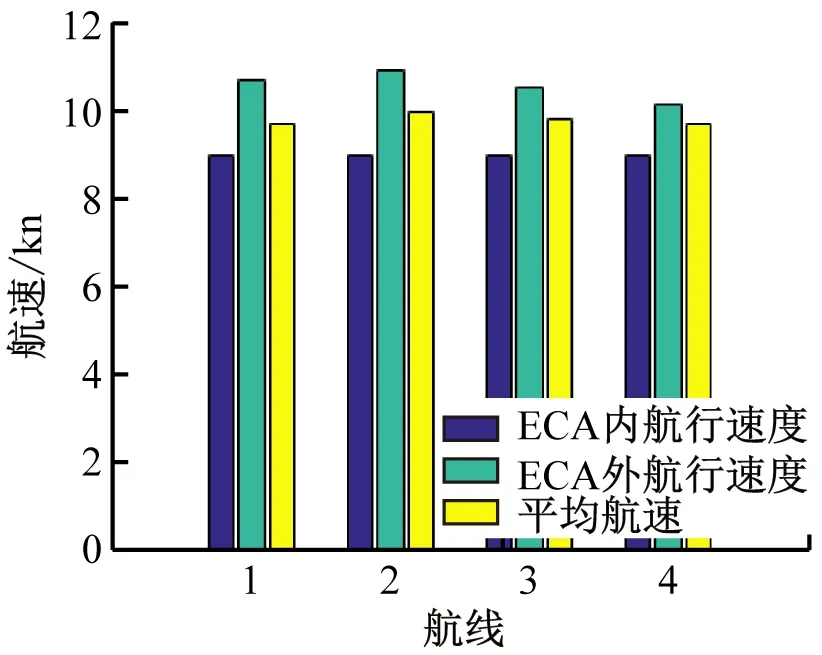
a) 航速对比

4 结束语

本文在考虑时间窗的不定期船舶调度模型的基础上，研究当前ECA和碳税政策对船舶运营的影响，构建航速和燃油可变的散货船调度模型，设计基于集划分理论的2阶段求解算法。在后续数值试验中发现：ECA政策的变动和碳税政策的落实不但会造成散货船运营利润的下降，还会促使承运企业提高ECA外的航速以换取ECA内的航行减速(从而减少对高品质燃油的消耗)。企业的这种航行方式会使燃油消耗总量增加，进而导致碳排放总量的增加。当前市场兴起的双油舱设计对于散货船运营而言并不长久。由于低硫油的价格过高，其价格波动对企业造成的风险会在这种模式下放大；企业被迫加大ECA区域外的航速，导致碳排放总量增加，违反低碳经济的初衷。不论从经济还是从环保效益的角度看，双燃油舱改建都存在很大局限性。企业经短期调整后，应积极寻求可代替方案，例如更换脱硫塔或启用新型船舶。