基于非负矩阵分解方法的海上交通特征

杨家轩， 吴京霖， 姜大鹏

(大连海事大学 a.航海学院; b.辽宁省航海安全保障重点实验室， 辽宁 大连 116026)

随着计算机技术和通信技术的快速发展，各领域的信息暴增，人类社会已进入大数据高速发展的时代，如何从大量的数据中发现潜在的特征，把握区域事件的发展规律已成为相关学者研究的焦点。近年来,航运信息的发展为海上交通领域积累了海量的数据，其中以船舶自动识别系统(Automatic Identification System, AIS)为主的船舶历史数据扮演着重要角色。AIS的广泛应用不仅提高船舶航行的安全性,而且其数据能较好地反映港口水域船舶海上交通信息，分析大量的位置信息、航线数据和AIS 数据等，尤其是AIS数据，不仅数据量大，而且数据之间存在相互关联。[1]结合数据挖掘技术，在海上交通工程的基础上，将船舶位置空间、时间、船型和船速等属性有机融合进行联合聚类，以识别重点水域,发现典型特征，为实现智能水域监管和海上安全保障提供理论基础。

在对交通特征的研究中，时空数据的耦合特性逐渐受到关注。文献[2]利用信息采集软件和数据挖掘技术对大量的AIS数据进行分析，识别特定水域的船舶会遇态势，并分析该水域船舶会遇空间分布和时间分布。文献[3]引入k-means算法对数据设定时间维度上兴趣时间段的约束条件，提取兴趣位置点，实现对车与地理位置关系的挖掘。文献[4]根据船舶交通特点将船舶领域概念引入DBSCAN算法中，对比船舶簇的速度和交通流的速度，识别出拥挤区域。文献[5]结合AIS数据的具体特征提出时间切片化方法，在DBSCAN算法的基础上，综合考虑时间和空间要素，提出船载AIS数据时空聚类算法，并对实际数据进行分析。时空聚类现已成为海量时空数据分析的一个重要手段和前沿研究方向。[5-6]

船载AIS数据属于典型的时空数据，其所包含的船舶空间、时间和其他维度属性数据中蕴含着大量的潜在特征，单一维度的聚类很难发现数据中潜在的有用信息，多属性联合聚类分析已成为船载AIS数据挖掘的趋势。现有研究倾向于在已有聚类算法上，尤其是对DBSCAN算法进行改进，从而对海上交通特征的时空关系进行挖掘与分析，但当数据量增大时，聚类收敛时间变长，实现算法需消耗的内存也变大，且参数选取相对复杂。由此，本文提出利用非负矩阵分解方法对船载AIS数据进行时空联合聚类，挖掘海上交通特征和船舶行为模式，并联系实际进行分析。

1 数据处理

从海量数据中提取关注的信息，首先需对数据进行过滤和清洗。[7]在实际应用中，从数据库中获取的原始船载AIS数据集不能直接利用，需进行数据清洗与预处理。预处理的目的是将原始粗糙的数据转化为适合分析处理的形式，其过程有特征选择、维规约等。[8]

从AIS数据库中提取指定区域和指定时间段内的船舶静态信息和动态信息。本文选取MMSI、经度、纬度、UNIX时间戳、船型和航速等信息进行研究。

1) 船舶轨迹数据集T是指船舶水上航行所形成轨迹的数据信息集合，有

T={(time1,lon1,lat1),(time2,lon2,lat2),…,

(timeN,lonN,latN)}

(1)

式(1)中：timeN为第N个数据的UNIX时间戳；lonN为经度；latN为纬度。

2) 时间域是指根据固定时间段将研究的时间切片化，并做编号标记，时间域为

t={t1,t2,…,tM}

(2)

式(2)中：tM为第M个时间域的编号。

3) 区域是指根据水域的形状和航道，将研究区域划分成的若干个不规则的小区域，有

R={r1,r2,…,rM}

(3)

式(3)中：rM为第M个区域的编号。

4) 标记数据集是指将原始数据集各属性数据的值分别映射到区域、时间域上的标记组成的数据集合。

本文中提出一个船载AIS数据预处理框架，具体步骤为

1) 从AIS数据库中提取指定时间与区域间的船舶动态信息、静态信息和航次信息，形成初始轨迹数据集。

2) 筛除初始轨迹数据集中存在的错误、缺失的数据，将同一MMSI的AIS数据按时间戳排序并连接起来；以时间、航向和停靠点为依据，划分出在同一MMSI轨迹数据中的不同航次和进出港情况。

3) 研究的水域划分为若干个区域，将经度和纬度数据映射到区域中并标记；研究的时间段划分为若干个时间域，将UNIX时间戳转换为标准时间，样本数据映射到时间域后标记。

4) 构建标记数据集。

2 稀疏约束下的非负矩阵分解

2.1 非负矩阵分解

矩阵分解是实现大规模数据处理与分析的一种有效方式[9]，通过矩阵分解解决实际问题的方法有很多，如主成分分析(Principal Component Analysis,PCA)、独立成分分析(Independent Component Analysis,ICA)和奇异值分解(Singular Value Decomposition,SVD)等。[10]这些方法可通过迭代分解的方式，近似地将数据原始矩阵分解为2个较低维数矩阵的乘积，获得数据的特征，各有优势，但存在一个共同、明显的缺点，就是在分解过程中没有对分解的结果进行非负约束限制，这些算法分解出的结果通常存在负数，从数学计算的角度看该结果是正确的，但在实际应用中，分解得到的负值结果通常是没有意义的且无法解释。LEE等[11]提出非负矩阵分解(Nonnegative MaxtrixFactor,NMF)，其是一种新的矩阵分解的思想。该算法通过对基与系数施加非负约束，保证分解结果均为正值；基矩阵利用系数矩阵作为权重，重构原始矩阵。非负矩阵分解见图1，其基本原理如下：

对于一个m×n的非负矩阵Vm×n，存在一个非负矩阵Wm×k和一个非负矩阵Hk×n，有

Vm×n≈Wm×kHk×n

(4)

即

Wmk≥0;Hkn≥0

(5)

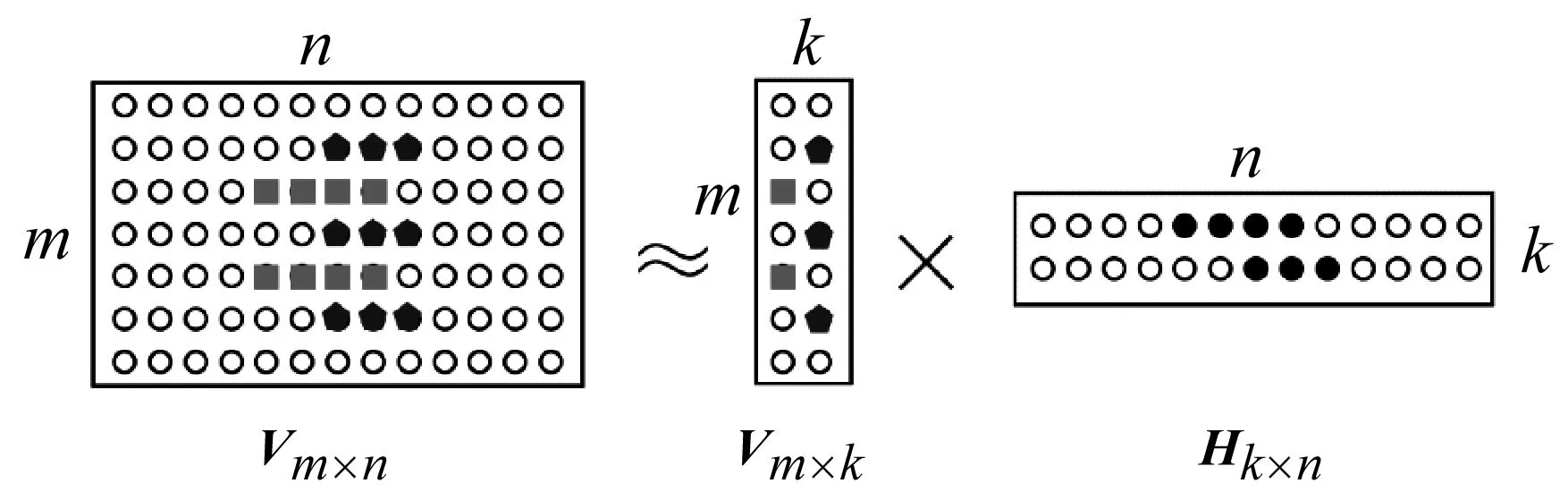
图1 非负矩阵分解示意

V中的列向量可解释为对基矩阵W中所有列向量的加权和，而权重系数为系数矩阵H中对应列向量中的元素。非负矩阵分解对数据的学习有部分组成整体的特性，因为分解所得元素只有“纯加性”，原始数据的整体由局部特征表示。由于其求解方法收敛速度快、左右非负矩阵存储空间小，因此,其能实现高维的数据矩阵降维处理，适合处理大规模数据。目前，NMF算法在聚类/数据挖掘、特征学习、图像分析、语音处理和生物医学工程等方面有很好的应用，在海事领域已有SAR图像船舶检测[12-13]、潮汐数据的分析与预测[14]等方面的应用研究。

2.2 非负矩阵分解迭代算法

非负矩阵分解是求解出2个非负矩阵W∈Rm×r和H∈Rr×n,使重构矩阵W×H与原始矩阵V之间的误差最小，实际上是一个最优化问题。问题的目标函数有很多，其中应用最广泛的是LEE等[15]提出的基于欧氏距离和Kullback-Leibler离散度的2种度量模型，衡量重构矩阵的近似化程度。

基于欧氏距离的目标函数定义为

(6)

基于Kullback-Leibler离散度的目标函数定义为

(7)

应用基于投影梯度法的交替最小二乘法[16]可求解非负矩阵分解问题。交替最小二乘法的算法模型如下：

1) 初始化W1,ia≥0,H1,bj≥0,i,a,b,j

2) Fork=1,2,…

(8)

(9)

该算法是在迭代中分别求解W和H,直至满足终止条件。投影梯度法的迭代规则[17]为

崩塌在SPOT5的影像解译特征：崩塌堆积体的平面形态多为弧形、扇形等。崩塌体后缘在遥感影像上阳坡为浅色调区块、阴坡呈浓重的阴影区带。崩塌堆积体上无植被覆盖，见图6(a)。

Hk+1=PΩ[Hk-ηHKPHK]

(10)

Wk+1=PΩ[Wk-ηWKPWK]

(11)

式(10)和式(11)中:PΩ[ξ]为ξ到凸集Ω={ξ∈R;ξ≥0}的一个映射;PHk和PWk分别为W和H的下降方向;ηHk和ηWk为相应的下降步长。该算法在迭代中同时求解W和H，直至满足终止条件，可达到收敛速度更快的效果。

2.3 稀疏约束的非负矩阵分解

“稀疏编码”旨在用少量的元素表示大量的有用数据，稀疏矩阵存储信息更高效，占用的资源少，且利于解释非负矩阵分解的结果。同类数据按列组成矩阵,矩阵的行向量对应某一特征,稀疏约束使其选择尽量少的非零行向量达到特征选择的目的。[18]非负矩阵分解得到的结果本身存在一定的稀疏性，但不够充分，因此，在NMF中加上稀疏约束，可提高分解结果的质量。本文通过在基于投影梯度法的交替最小二乘算法中，对基矩阵添加L0范数约束，提高NMF分解结果的稀疏度。问题的目标函数改写为

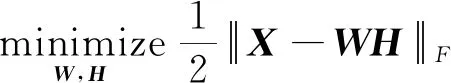
(12)

(13)

式(13)中：参数L是Wi中允许的最大非零项数。

基于以上讨论，提出在L0范数约束下，利用基于投影梯度法的交替最小二乘法的非负矩阵分解聚类算法为

Input：

标记数据集X∈Rm×n

结构参数options：

分解得到矩阵的秩K

公差tolerance

外部循环次数numIter

最大迭代数maxIter

最大非零项数L

output：

分解后的基矩阵W∈Rm×K，系数矩阵H∈RK×n

Steps:

1) 随机初始化矩阵H

2) 执行外部循环：

利用非负最小二乘求解基于H对X的非负分解结果WT

fori，…，k

将Wi中最小的D-L个数值更新为零

根据得到的W，对H进行重新编码

矩阵梯度=WT(WH-X)

(14)

根据式(14)进行迭代，直至满足条件

3 实例分析

3.1 数据预处理

本文选取天津港水域真实AIS数据作为研究对象。

1) 研究海域为：经度117°35′35″E ～ 118°43′E，纬度38°3′30″N ～ 39°34′30″N。参考交通流走势，将该区域划分为38个不规则区域，划分详情见图2。

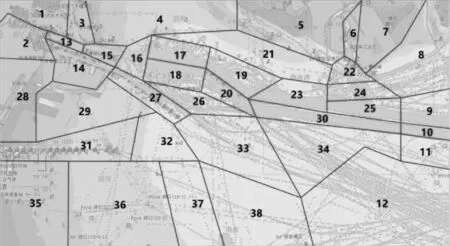
图2 AIS样本和区域划分结果

2) 研究时间为：2018-01-01T00:00—2018-01-06T24:00。考虑到研究海域的大小和船舶航速，在该时间范围内，按24 h制，每4 h划分为一个时间域，共划分36个时间域，编号详细情况见表1。

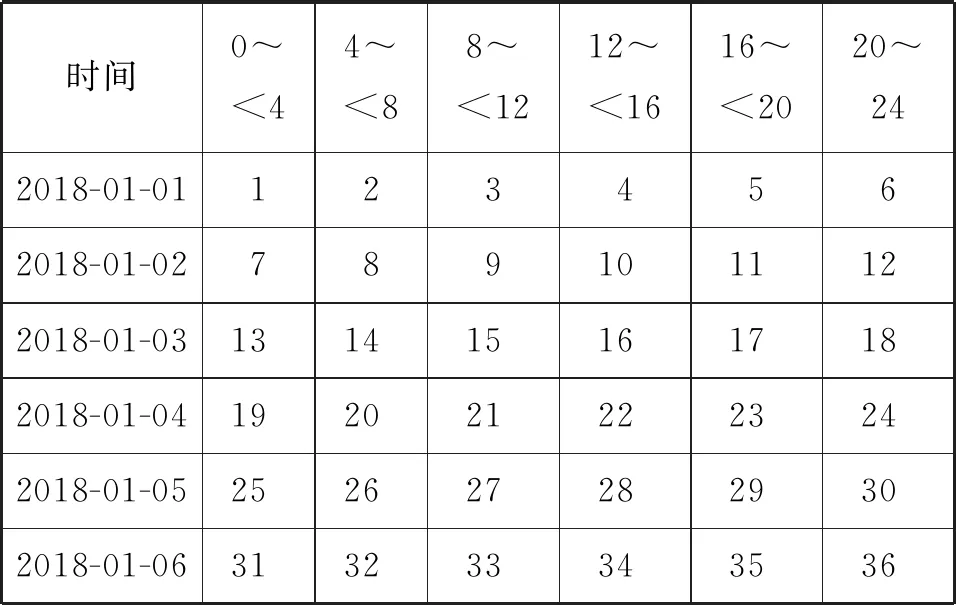
表1 时间域划分与编号结果 h

在经过数据清洗之后，获得998艘船舶的共 185 818条样本数据，处理前的AIS数据列表见表2，处理后的标记数据列表见表3。

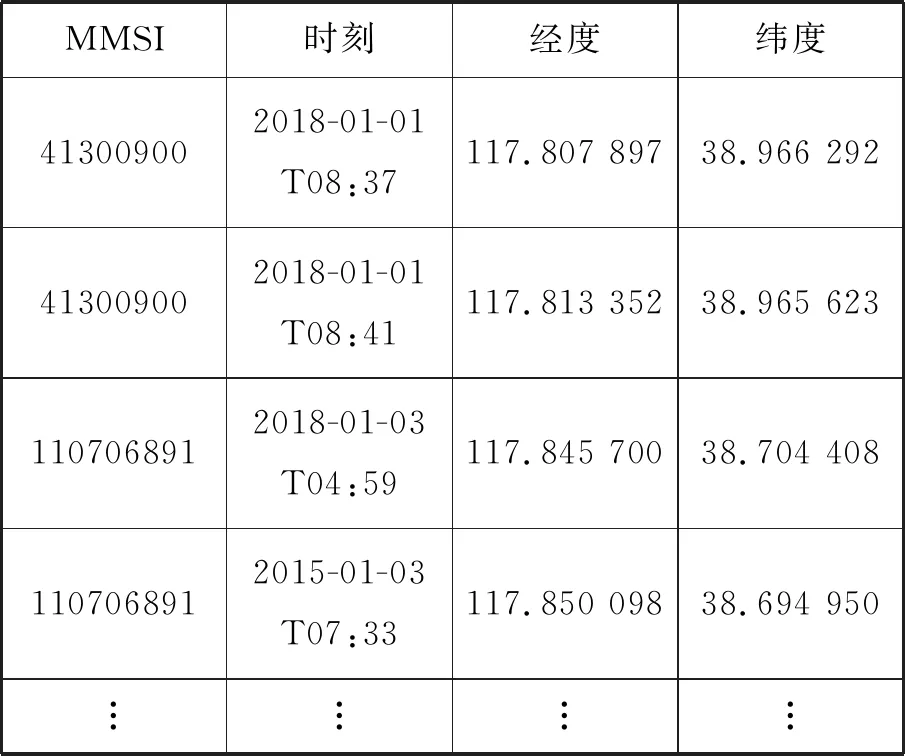
表2 处理前的AIS数据列表 (°)

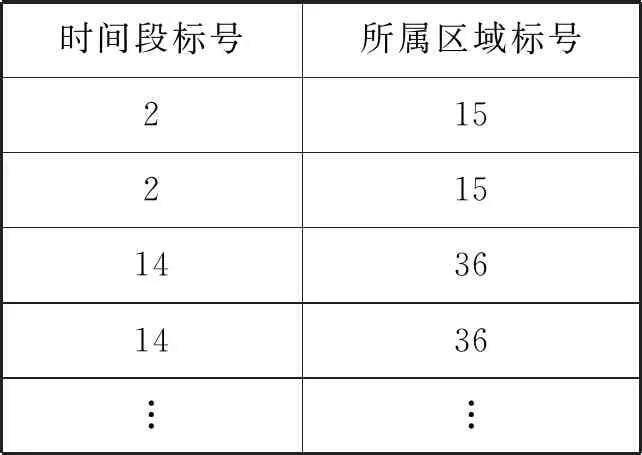
表3 处理后的标记数据列表

3.2 时空数据聚类结果与分析

将AIS数据分为进港、出港和全部航次样本数据集，分别进行分析。以时间-空间属性矩阵为例,试验采用SQLite 3.5作为后台数据库，利用PyCharm 2019进行数据清洗和预处理工作，采用MATLAB R2015 a 完成聚类算法的开发。船舶时空数据集未进行数据频率上的约减，即同一艘船舶在时间段tM内，在区域rM内产生的所有符合研究条件的时空数据均纳入研究数据集中，计入区域rM在时间段tM内的船舶流量密度。

当L=4时，L影响分解结果的稀疏度和误差，通过反复试验，结合分解结果的可解释性，选取L=4，基矩阵的稀疏度为0.690 7。当L=4时，对K的不同取值做30次独立重复试验，得到各K值下的平均误差见表4。

由表4可知:当K值增大时，矩阵分解结果的误差减小。对于此次试验的数据集，当K≥6时，数据矩阵分解的误差变化小于0.03。K值决定联合聚类得到的共簇数量，当K值不断增大时，可能会造成结果冗余。综上所述，选取K=6、L=4(即原始数据集聚类得到的时空共簇数目为6，每个类中包含的属性项维数为4)，分别对全部航次时空数据和出港船舶时空数据进行聚类分析。

表4 不同K值下的试验平均误差值

3.2.1以位置属性为分析对象的聚类结果分析

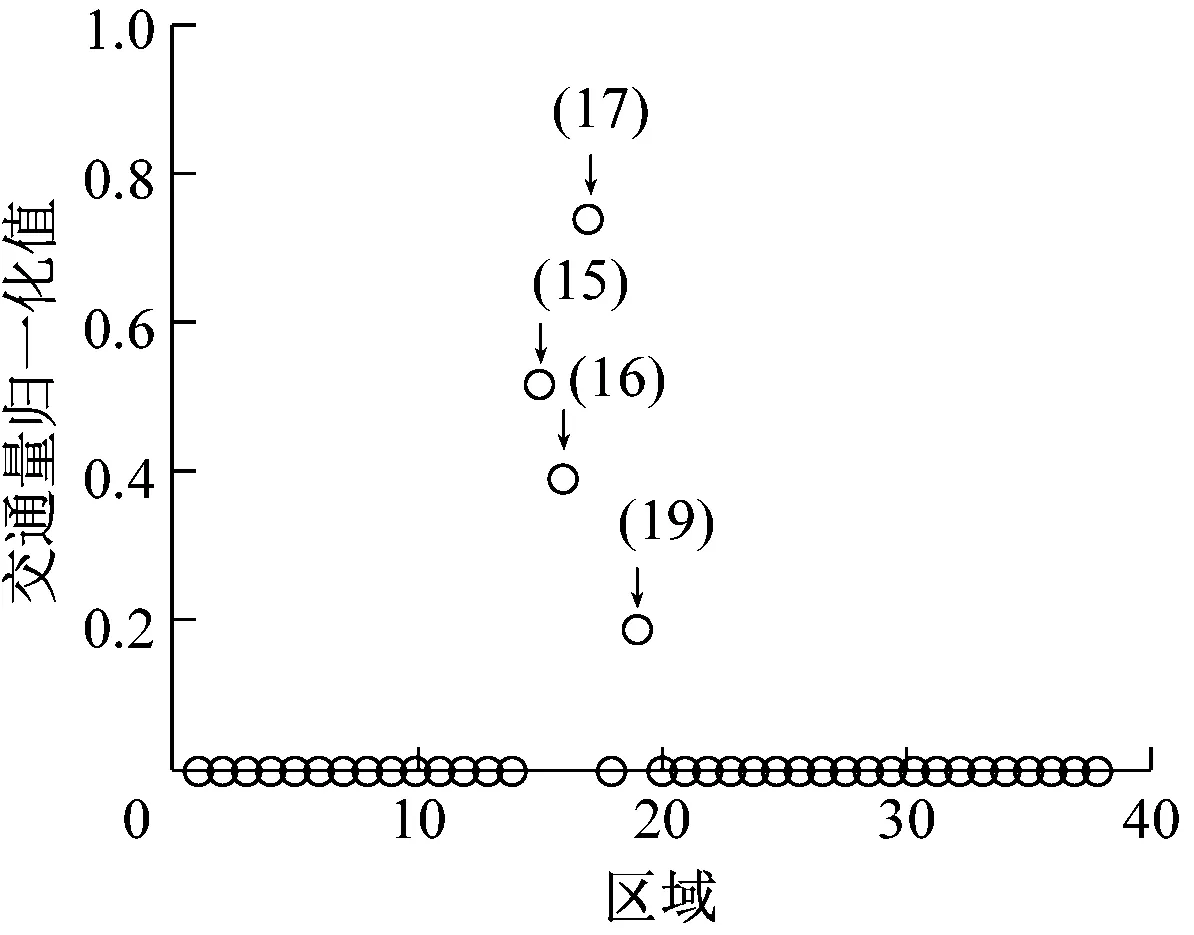
为尽可能多地得到研究海域中的空间特征，使用全部航次的时空数据矩阵进行聚类分析，各类中的区域标记示意见图3。

a)类簇1

由图3可知：聚类结果结合实际的海域功能区可得到以下信息：

(1) 类簇1包括区域15、区域16、区域17和区域19，这是一条由区域19经过大沽口北锚地进入天津港港口的一段航路；

(2) 类簇2包括区域10、区域18、区域20和区域30，此区域为天津港主航道出港航路；

(3) 类簇3包括区域9、区域19、区域23和区域25，此区域为天津港主航道进港航路；

(4) 类簇4包括区域6、区域8、区域22和区域24，这是一条进出曹妃甸港区的航路；

(5) 类簇5包括区域12、区域14、区域27和区域33，这是一条途径区域12、区域33和大沽口航道进出大沽口港区的航路；

(6) 类簇6包括区域3、区域13、区域15和区域16，此区域为进出天津港东疆、南疆和北疆港区的航路。

图3中，类簇1和类簇3中均包含区域19，类簇1和类簇6中均包含区域15和区域16，出现这种结果的原因有2个：

(1) 与区域的划分有关，即1个区域中涵盖2种船舶运动类型的区域，如区域15和区域16，进出港口的航道均在这2个区域内；

(2) 与聚类数K和每一类中属性项数L的取值有关。以类簇1和类簇3为例，2个类代表的区域见图4。由图4可知:类簇1和类簇3组成一段完整的航路，但在聚类表示中，由于选取的每一类中的属性项数为4，即每一个类由最相关的4个区域表达，而该航路经过的区域数量大于4，实际是通过类簇1和类簇3这2个类进行表示，因此，在对聚类结果上出现区域的重叠。

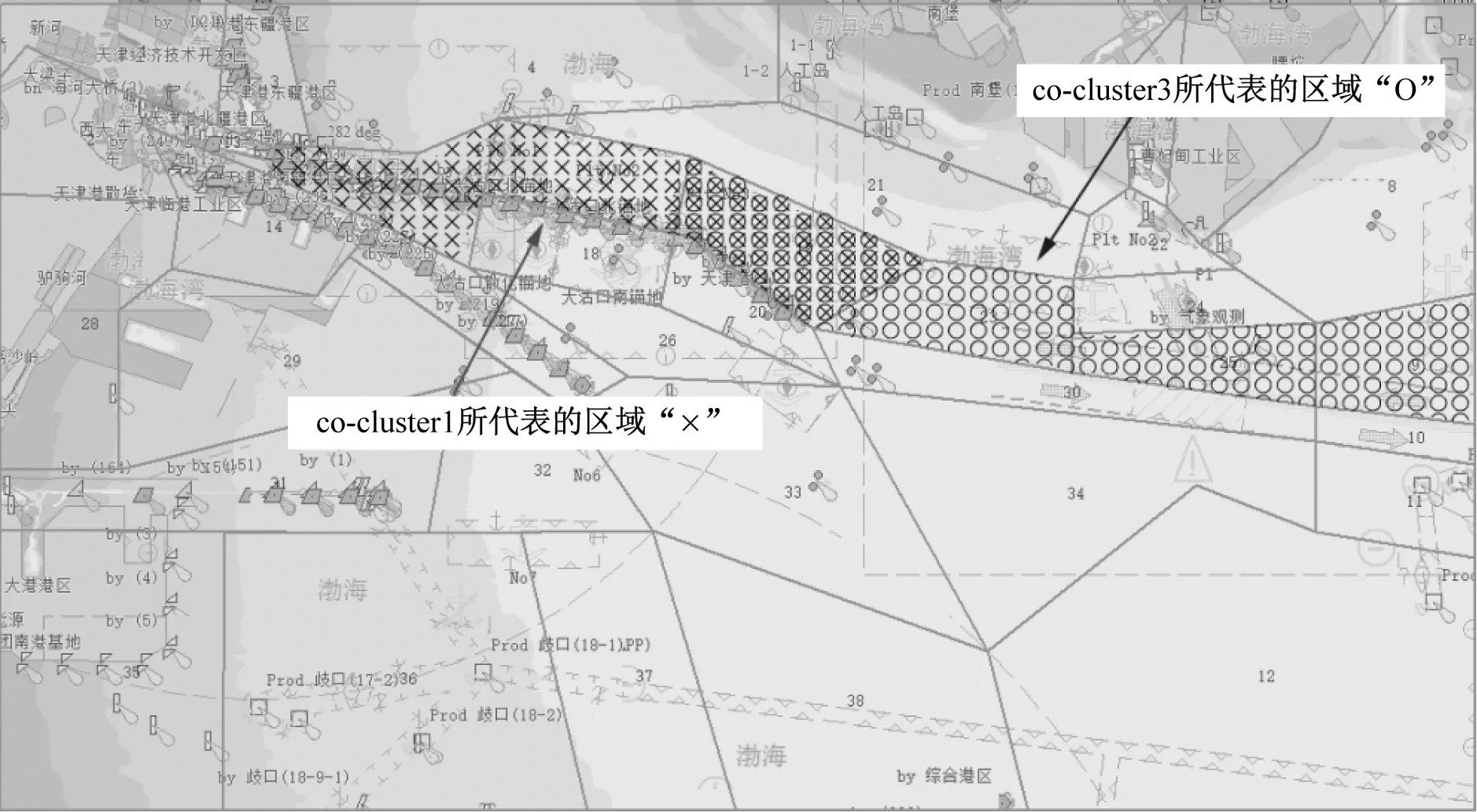
图4 类簇1和类簇3涵盖区域示意

从聚类的层面看，NMF属于“软聚类”算法，1个元素可属于多种类型；从实际意义的角度分析，同一个区域中可能有一定比例的、不同运动模式的船舶航行。因此，在利用时空数据聚类对船舶与位置属性的整体关系进行分析时，1个区域属于多个类是符合水上交通的实际情况的；从数值关系的层面看，在类簇1和类簇3中，区域19的船舶占比之和与船舶进入该区域的前段航路(区域23)占比接近，因此，该航路可看成被“拆分”在2个类簇中表达，此现象也符合NMF算法“由局部构成整体”的特性。

3.2.2以时间属性为分析对象的聚类分析

以研究船舶出港流量变化的时间规律为例，使用出港船舶的时空数据矩阵进行聚类分析，时空聚类结果的区域标记示意见图5。

a)类簇1

以类簇3为例，对该类中的区域在时间模式下的波动情况进行分析，详细情况见图6。图6中：每条线代表一个区域；x轴为1～6日划分的36个时间域；y轴为时间段内区域中的船舶流量数值；类簇3中包含的区域为区域8、区域10、区域22和区域30，包括天津港出港主航道的一段航路和进出曹妃甸港区的一段航路。

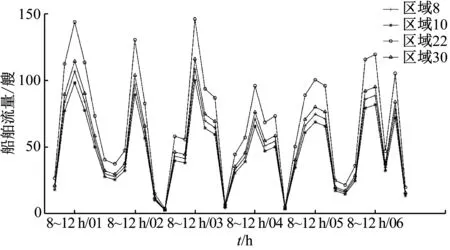
图6 类簇3聚类关系中船舶流量随时间波动的情况

由图6可知:在类簇3包含的区域关系中，区域8、区域10、区域22和区域30的船舶出港流量变化趋势接近，说明有一部分船舶航行途经该类的区域8、区域10、区域22和区域30。结合实际分析，其反映的隐含关系是曹妃甸港区和附近水域船舶驶离曹妃甸时的航行方法，即由开敞性泊位区(区域8)或东侧锚地(区域22)内离泊，通过第三通航分道，驶向警戒区(区域30内)，由第一通航分道(区域10)内驶离曹妃甸港区。由图6可知：在1～6日这6 d中，船舶以该航行方式出港的峰值也呈现一定的规律，即在每天的8～12 h时间段内均处于当日船舶出港最高峰，夜间航行出港的船舶数量相对较少。

4 有待进一步研究的问题

4.1 聚类特征数K的选取

目前，对于确定聚类特征数K以获得最佳的聚类效果尚没有很好的解决方法，因为,K的取值与数据集的类型有关，在对非负矩阵进行分解时，选取K值的约束条件为

K

(15)

式(15)中：当K较大时，降维效果不显著，特征不突出；当K≪min{m,n}时，特征明显，但易导致忽略一些特征信息。目前,通用的方法是选取一系列K值分别进行试验，将获得的最佳辨识结果的聚类簇数作为K的取值。

4.2 区域划分

对于区域划分问题，特征聚类结果的可读性受“规则网格区域”或“不规则区域”的划分方式的影响不大，更多的是与区域划分精度相关，例如在区域属性的聚类分析中，区域划分精度低，会出现1个区域分别隶属于多个类簇的情况，例如图3中区域15和区域16均隶属于类簇1和类簇6，这种结果在规则和不规则的区域划分中均会出现，但在低精度的区域划分中出现的频率更高；若划分精度过高，矩阵特征维数增加，K值和每个类中特征维数L的选取难度增大。

4.3 最优化问题

非负矩阵分解是一个约束优化问题，矩阵分解的迭代收敛速度与目标函数的选取和稀疏约束的方式有关，因此,目标函数与稀疏约束函数等的优化问题是进一步研究的方向。

5 结束语

海上交通时空数据存在耦合性，利用这种特性研究海上交通数据的时空分布特征和规律可发现其隐含的信息，对航道规划和水上安全等工作的正常开展具有重要的现实意义。本文以计算机数据挖掘为研究手段，提出采用非负矩阵分解算法对大量的AIS数据在时间和空间2个属性上同时进行约束聚类，探索海上交通数据时间和空间2个维度之间的关系，利用真实的AIS大数据集进行试验，并对已有算法进行L0范数约束的改进，以达到更好的突出特征的效果，最终得到研究水域的主要航路，不同区域之间相近的船舶流量波动关系，以及针对途径区域8、区域10、区域22和区域30驶离曹妃甸港区的船舶通常在8～12 h达到离港峰值等信息，聚类结果与实际相符，证明方法是可行的。该方法可用于挖掘研究水域的船舶行为模式，分析船舶的运动规律等，为水上交通安全监管和海上安全保障相关研究提供一种新的思路。