基于关联分析的船舶事故关键致因识别
2021-01-06蒋少奇陈伟炯谢启苗汪金辉张盼飞
蒋少奇, 陈伟炯, 谢启苗, 汪金辉, 张盼飞
(上海海事大学 a.海洋科学与工程学院; b.海洋公共安全研究中心; c.商船学院, 上海 201306)
重大船舶事故的研究一直备受国内外学者的关注,目前,主要基于统计模型对事故数据进行分析[1-2],如泊松模型[3]、负二项(Negative Binomial,NB)模型[4]、有限混合回归模型和分位数回归方法等。[5-6]以统计分析作为事故的研究基础,在事故分析中发挥重要作用。但统计方法往往假定致因间相互独立,导致可能出现量化分析结果与实际不符的情况。[7-8]事故的发生无疑是复杂致因关联作用的结果,结合关联分析方法可有效提高统计结果的准确性。[9-11]目前,关联分析方法已在交通运输领域得到应用,如:赵怀鑫等[12]提出基于灰熵法研究国民经济宏观因素与公路货运量和货物周转量之间的关联关系;孙丽萍等[13]基于模糊证据推理和改良灰色关联度的风险排序方法对浮式生产储卸油装置(Floating Production Storage and Offloading,FPSO)原油舱的失效模式进行风险辨识,通过TOPSIS(Technique for Order Preference by Similarity to an Ideal Solution)思想解决失效模式和影响分析(Failure Mode and Effects Analysis,FMEA)相同风险优先数(Risk Priority Number,RPN)的问题;YAZDANI等[14]针对复杂的供应链决策问题,提出基于工作效能(Quality Function Deployment,QFD)和灰色关联分析(Grey Relation Analysis,GRA)融合的多属性决策支持模型,创新性地解决在区间值模糊环境中,由于庞大距离的计算量使决策者难以获得结果的问题。这些研究成果为GRA的应用奠定重要基础。
GRA主要通过期望结果与实际序列间的距离确定相似程度,从而准确地反映因素间的关联性。但传统关联方法缺乏对结果的验证分析,可能出现相同关联系数值的情况,导致部分因素无法进行关联度排序。基于熵权灰色关联与逼近理想解排序的故障树分析(Technique for Order Preference by Similarity to an Ideal Solution-Fault Tree Analysis,TOPSIS-FTA)方法提供一种思路[13],将故障树分析法的最小割集与TOPSIS方法的理想解相对贴近度相结合,得到最小割集作为基本关联事件的相对贴近度,优化灰色关联结果。与统计模型分析方法相比,其对样本量大小和规律性无特殊要求,有较好的实用价值。[15]此外,优化的关联分析结果可更准确地反映因素关系量化情况,完善关联结果的验证,为进一步探究事故内部因素作用机理制定有效预防措施提供参考。故本研究将建立船舶事故致因层次分析模型,并从关联分析角度构建关键致因识别框架。针对灰色关联结果,基于TOPSIS-FTA和德尔菲(Delphi)法进行优化,再结合权重指标得到最终关联系数矩阵和关联度序列,探究一种基于关联分析的船舶事故关键致因识别基本方法。
1 事故致因层次分析模型
船舶事故研究多集中于不同地区船型的风险或后果评估与预测,缺乏对致因的关联分析与综合评价。由于船舶事故涉及众多因素,主要通过统计分析和专家经验确定致因,如:吴伋等[16]基于文本挖掘技术,根据419起内河航道船舶碰撞事故统计报告明确事故致因;殷杰[17]基于系统理论事故模型和流程方法(System Theoretic Accident Model and Processes,STAMP),从体系-系统的视角多层次分析“桑吉”轮事故致因;BAKSH等[18]利用历史数据和专家经验确定北极航行风险因素。
本文通过事故报告分析和专家调研,发现船舶事故的发生与航行状态和直接致因密切相关,得到碰撞、搁浅和船体受损等事故的主要直接致因及在近岸或受限水域锚泊、在开阔水域航行和正在进行装卸货作业等主要航行状态。并建立船舶事故致因层次分析模型,分为影响因素和航行状态2个指标层与其各7个分指标层,见图1。
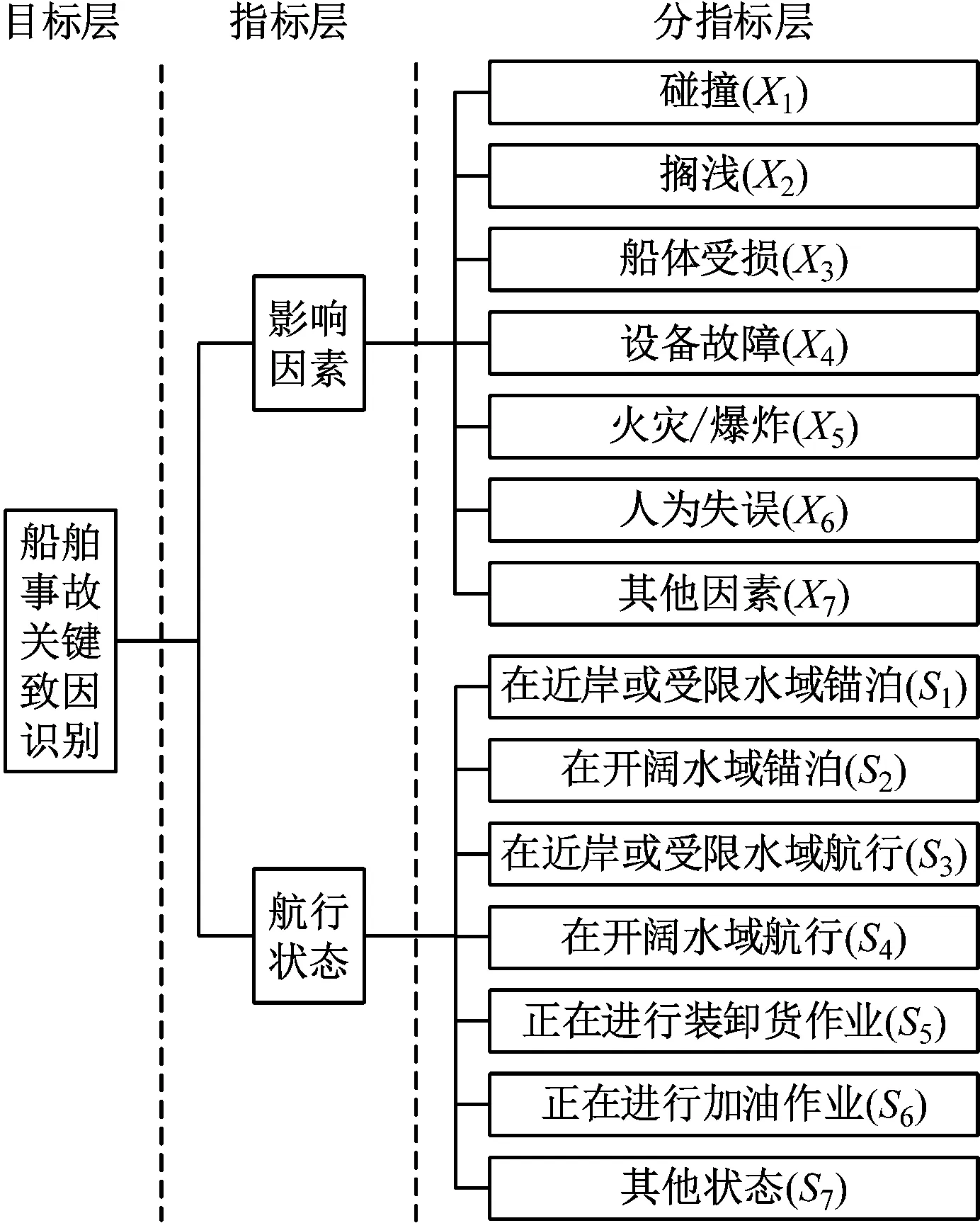
图1 事故致因层次分析模型
2 关联分析框架
由于在事故分析中,往往无法完全掌握各种因素类型,故船舶事故致因属于灰色系统,通过熵权灰色关联法可得到因素关联性。其中,权重系数作为重要度量值,在多因素综合分析中十分重要,而熵权法由于计算简便且结果客观,得到普遍应用。此外,针对灰色关联结果可能出现的关联系数值相同的情况,采用TOPSIS-FTA方法得到以最小割集为基本单位的相对贴近度即关联系数矩阵,优化灰色关联结果。其中,为使结果更符合实际,通过Delphi法量化专家经验确定优化系数,得到最终关联系数矩阵和关联度序列。鉴于此,本文提出基于熵权灰色关联与TOPSIS-FTA相结合的关键致因识别方法,构建关联分析框架,见图2。
3 基于熵权灰色关联与TOPSIS-FTA相结合的关键致因识别方法
针对船舶事故复杂致因的关联问题,在构建的事故致因层次分析模型基础上,提出一种熵权灰色关联与TOPSIS-FTA相结合的船舶事故关键致因识别方法。
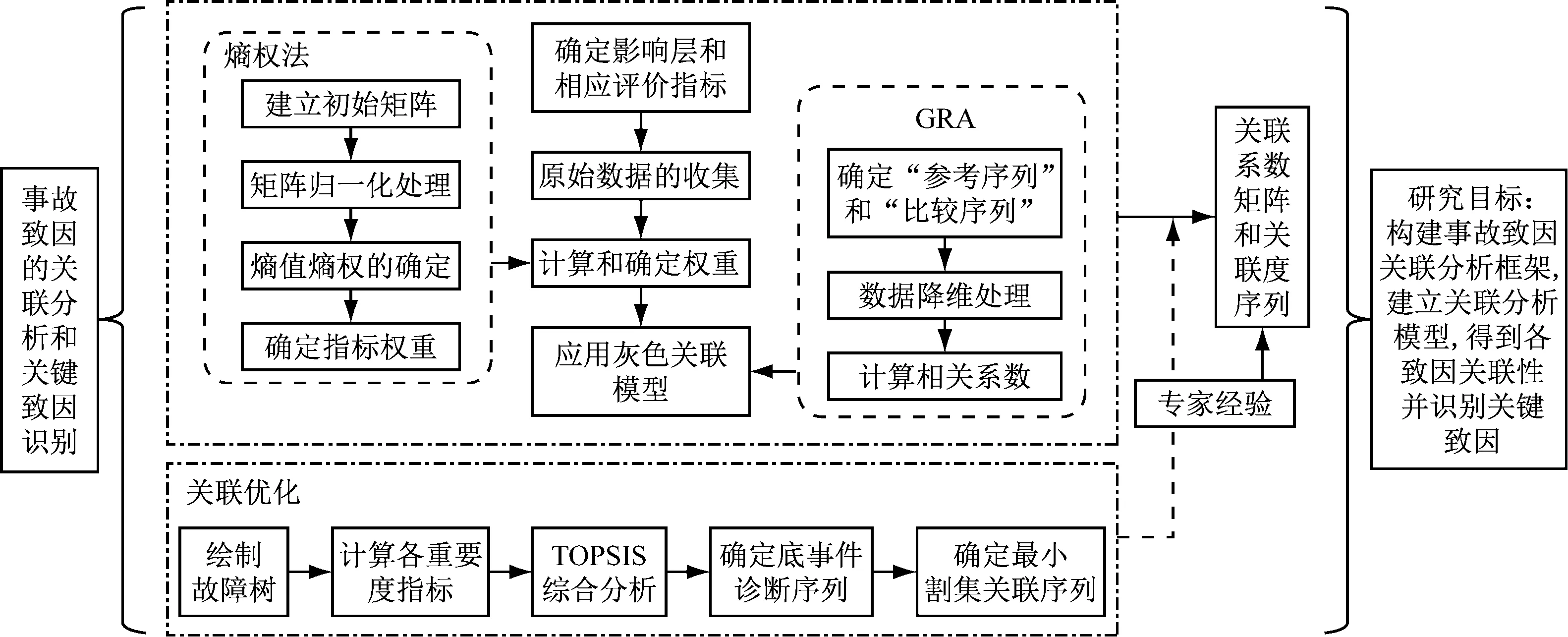
图2 事故致因关联分析框架
3.1 确定权重向量
1) 对统计整理的原始数据进行标准化处理。并设有m×n个评价指标,则标准化后的判断矩阵为R=(Pjj)m×n(i=1,2,…,m;j=1,2,…,n)。
2) 计算第j项指标的熵值和权重为
(1)
式(1)中:为保证ej∈[0,1],令Pij=0时,ej=0。
3.2 计算灰色关联系数矩阵
GRA是通过计算期望结果与比较序列间的距离来确定相似程度,从而揭示关联性。
设P0={P0(k)|k=1,2,…,n},Pi={Pi(k)|k=1,2,…,n}
(2)
式(2)中:P0为GRA中的参考序列;Pi作为比较序列,并计算指标的关联系数ζi为
(3)
式(3)中:ρ为分辨系数,0≤ρ≤1,ρ越小分辨率越大,此处取0.5。
3.3 建立故障树
由于传统故障树往往是对单一指标的分析,使得评价序列陷入局部最优的情况[19],故通过故障树分析确定最小割集为事故发生的基本关联事件,再依次求得其结构重要度、关键重要度和概率重要度指标。并结合事故致因层次分析模型,以事故发生为人为指定的顶事件,各指标层为中间事件,分指标层为底事件。假设导致事故发生的中间事件即指标层有K个,相应的各分指标层有S个,建立事故发生故障树,见图3。

图3 事故发生故障树
3.4 计算理想距离和相对贴近度
通过基于TOPSIS-FTA方法计算最小割集的相对贴近度,优化灰色关联结果。
1) 通过计算基本关联事件的3个重要度指标来建立初始矩阵。假设有S个基本事件,每个基本事件有T个指标值,第i个基本事件的第j个指标值记为rij,按行进行标准化并结合指标权重得到加权矩阵
H=(Vij)s×t=(wj×hij)s×t
(4)
式(4)中:第i个基本事件的第j个加权指标值记为Vij;wj为指标权重;hij为rij的标准化值。
(5)
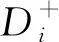
i=1,2,…,s;j=1,2,…,t
(6)
3.5 确定最终关联系数矩阵及关联度
基于Delphi法确定优化系数,得到最终关联系数矩阵,每行基本事件关联系数记为θi。结合船舶状态指标权重计算得到影响因素的关联度序列ri为
i=1,2,…,m;j=1,2,…,n
(7)
式(7)中:为确定优化系数a和b,将海事院校和机构专家分为资深船长、海事专家和安全领域学者等3组,对计算结果的实际符合程度进行评估。
4 实例分析与验证
将船舶事故关键致因识别方法应用于油船溢油事故中,对1970—2017年溢油量为700 t及以上的重大油船溢油事故统计数据(源自国际油船船舶所有人污染联合会2017年油船溢油事故报告)进行分析,并从研究结果对方法适用性进行验证。
4.1 实例分析
4.1.1确定权重向量
由事故致因层次模型分析可得船舶溢油事故统计数据,见表1。
由权重式(1)计算可得船舶状态指标的事故权重,见表2。

表2 溢油事故致因指标权重表
4.1.2计算灰色关联系数矩阵
假设存在影响因素使事故必然发生,为参考序列X0,并按影响因素行进行标准化,计算结果见表3。
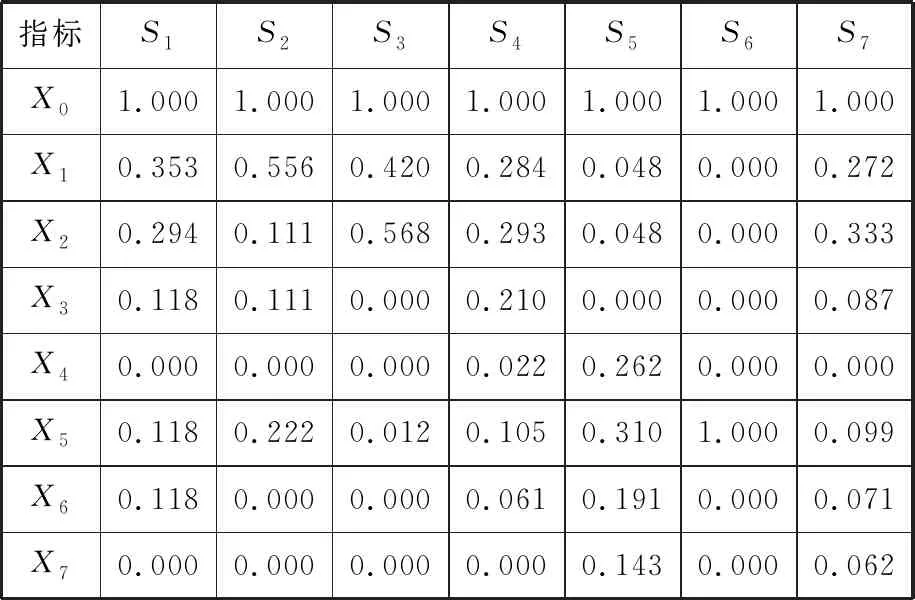
表3 标准化数据统计表
通过式(2)计算各实际影响因素到参考序列的距离,得到关联系数矩阵ζ为

(8)
式(8)中:矩阵每行分别为影响因素指标X1~X7;每列分别为船舶状态指标S1~S7,矩阵值为计算所得的因素间关联系数。
4.1.3计算相对贴近度
(1) 通过事故发生故障树的分析来确定最小割集为基本关联事件,如在开阔水域航行时发生碰撞;
(2) 计算各基本事件的3个重要度指标,建立初始矩阵,并结合指标权重,通过式(3)和式(4)计算得到相对贴近度矩阵C为
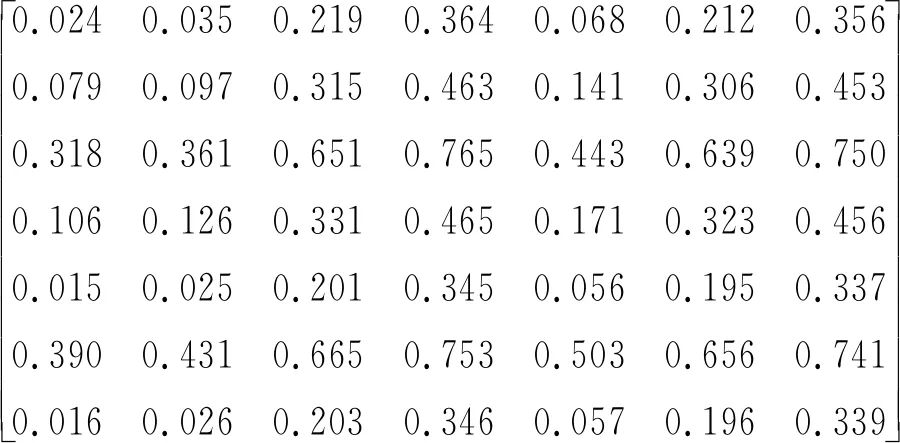
(9)
式(9)中:每一行为影响因素;每一列为船舶状态;矩阵数值为各最小割集的相对贴近度。
4.1.4确定最终关联系数矩阵及关联度
通过相对贴近度矩阵优化灰色关联结果,由式(5)计算得到事故致因的关联矩阵θ为

(10)
再结合船舶状态指标权重,计算得到影响因素指标的关联度矩阵r为
[0.536 0.540 0.414 0.347
0.556 0.411 0.310]T
(11)
基于Delphi法和成对比较的9级标度法来量化专家经验[20]确定优化系数。为避免成对比较次数过多影响专家判断,提取相同系数值出现次数最多的行列项即X2、X3和X4与S2、S3和S6,作为矩阵特征量进行成对比较,共9组。最后,依次得到3组共15名专家的打分,标准化后求得优化系数分别为0.8和0.2。而在关联矩阵中每一行为影响因素,每一列为船舶状态,矩阵数值为各因素的关联系数,因素越相关则关联系数值越大。
通过上述计算,可得船舶状态指标在各关联因素中所占的权重。S5占据最大的权重为36%,其次是S1为22%。而对于因素间的关联性,关联系数矩阵见图4。图4中:标签为各关联系数值及其对应的事故数,比较可发现统计数据中并没有发生事故的因素组合,却有着导致事故发生的关联效应。如在S2时设备故障,其并没有在事故统计数据中体现,但却与事故的发生有着关联系数为0.292的关联性。结合航行状态指标权重求得影响因素的关联度序列,见图5。
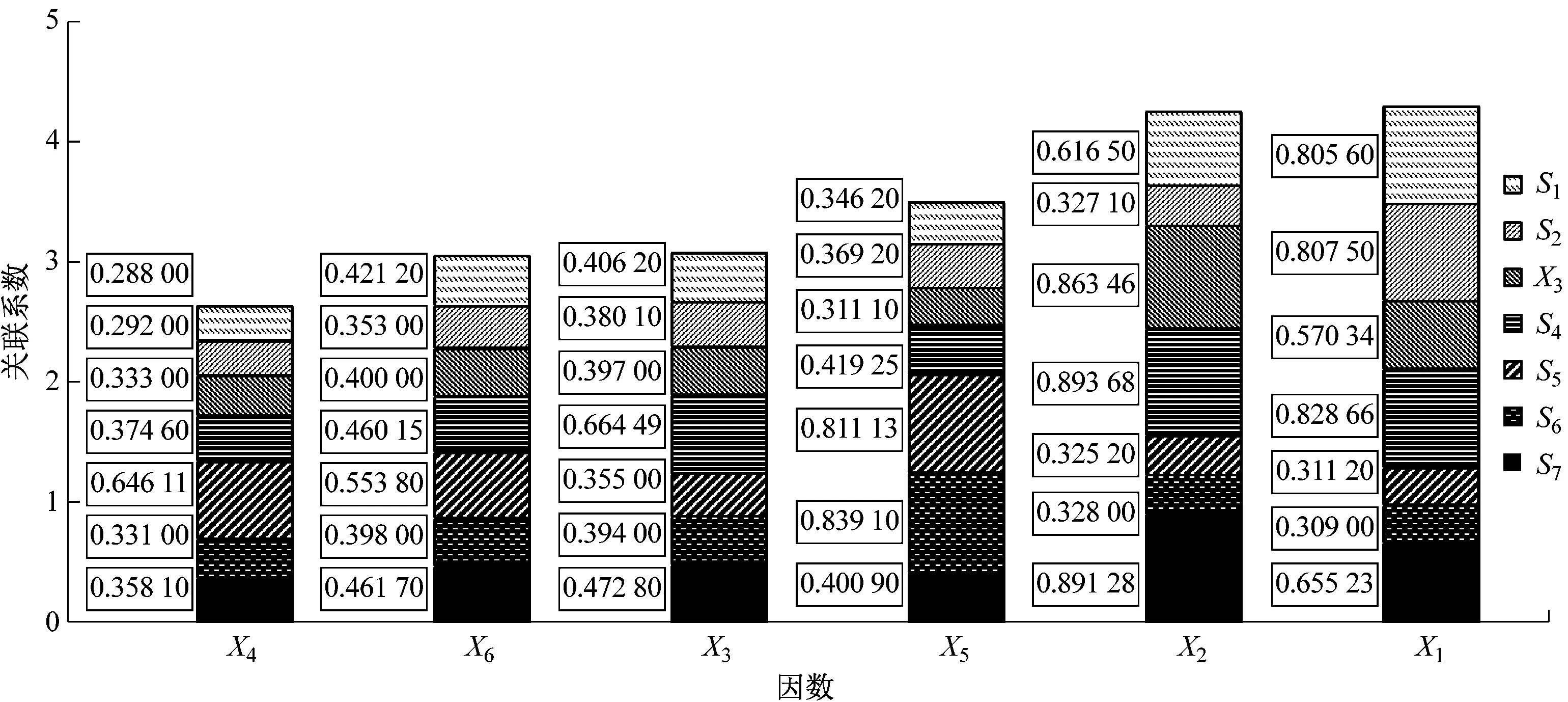
图4 因素关联系数

图5 关联度序列图
由图5所知:X5、X2和X1是引发溢油事故的关键致因。其中,X5的关联度稍高,且与其关联性最大的船舶状态是S6。因为,装卸的石油和其相关产品具有易燃易爆的性质[21],一旦部分泄漏导致起火将引发重大溢油事故。而X1与其对应的S1和S2。因为,在锚泊过程中驾驶人员极易放松值守而造成碰撞,且若发生碰撞可能会造成船体受损,设备故障等一系列附加关联因素,使得发生溢油事故的概率大大增加。此外,其他事故致因的影响相对较小。最后,为使关联度评价结果更清晰,将关联度与事故统计数进行标准化比较,见图6。图6中:折线为关联度;数据点为相对应的事故统计数。由图6可知:发现事故统计数较少的因素却有着导致事故发生较强的关联效应如X6、X4等。
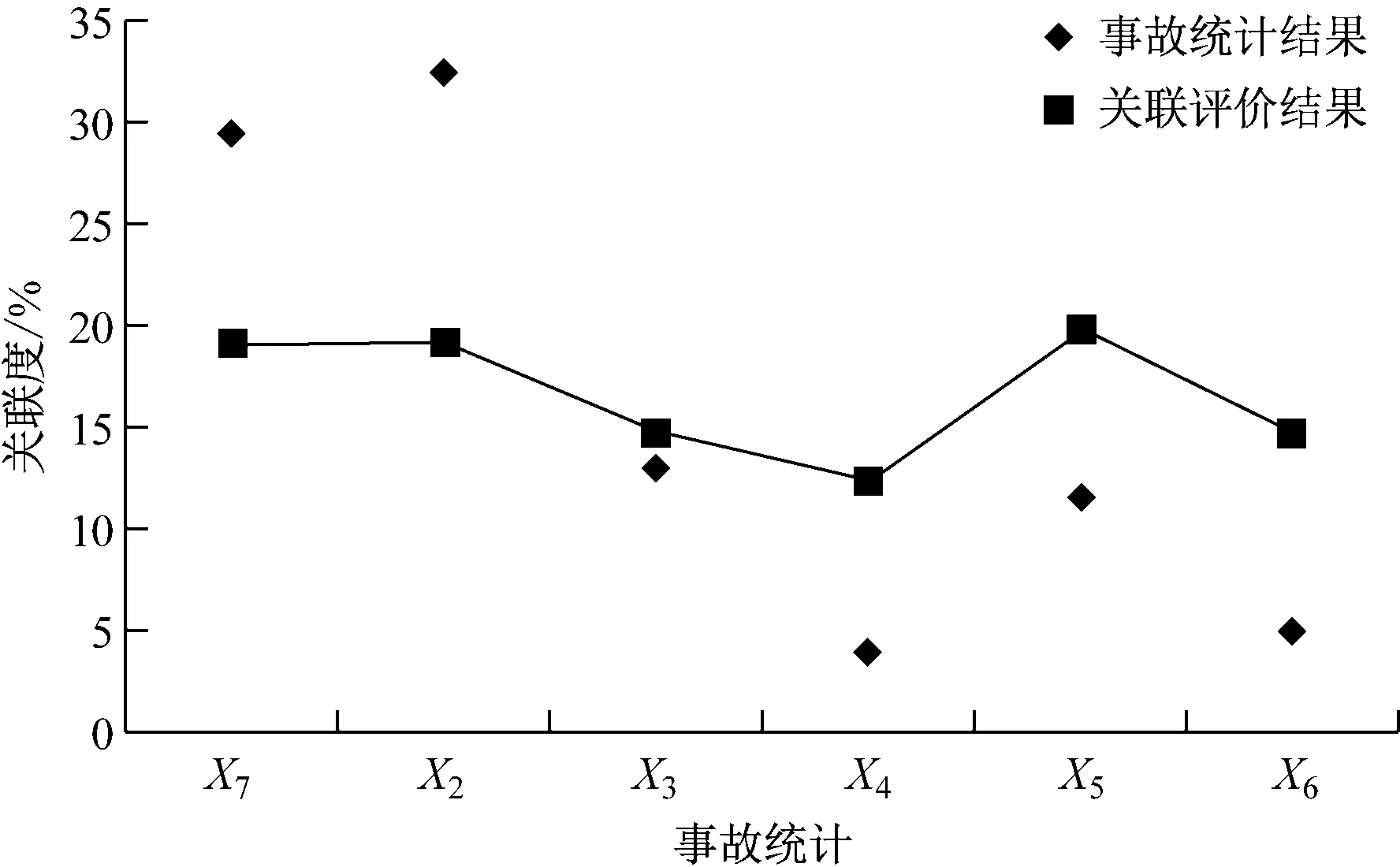
图6 结果比较图
4.2 结果验证
基于熵权灰色关联与TOPSIS-FTA相结合方法得到油船在加油作业时发生X5、S1时发生搁浅或在锚泊状态时发生X1是事故关键致因。且在《IMO溢油风险评价手册》中,也是分别得到重点关注的航行状态和风险评价的主要影响因素[22],结果表明符合实际,验证研究方法的适用性。
5 结束语
1) 本研究提出一种基于关联分析的船舶事故关键致因识别方法,为事故预防措施的采取提供参考。并通过识别框架构建和实例运算得到,油船在加油作业时发生X5、在锚泊状态发生X1和在航行状态发生X2是溢油事故的关键致因。
2) 利用TOPSIS-FTA方法确定最小割集为基本关联事件,得到相对贴近度矩阵,对灰色关联结果进行优化,解决可能出现相同关联系数值情况。并基于Delphi法确定优化系数,量化专家经验,使计算结果更符合实际。
3) 基于关联分析可发现事故统计数较少的因素,却有着导致事故发生较强的关联效应如人为因素、设备故障等,及其对应的关联船舶状态如正在进行装卸货和加油作业,可为后续在船舶航行风险建模中指标的选取提供参考。
