黄骅港限制性双向航道船舶交通组织优化

张新宇， 王志强， 邓志鹏

(大连海事大学 海上智能交通研究组， 辽宁 大连 116026)

神华黄骅港煤炭港区5万吨级重载双向航道工程于2012年10月26 日通过海事部门验收并通航成功。[1]但是,鉴于航道自然地理条件的限制，根据港口有关规定，航道部分航段只允许单向通航，其余航段实行有条件的双向通航。[2]由于航道船舶交通状况等条件的限制，当前该港区仍执行单向通航。为此，如何提高该港区限制性双向航道船舶进出港作业效率是亟待解决的问题。

目前，针对黄骅港煤炭港区航道船舶交通组织优化问题的研究较少，大部分研究集中在黄骅港煤炭港区航道通航安全和通过能力分析、评价或仿真方面[3-6]，缺少从全局角度开展对航道水域船舶交通组织方法的理论研究，因此不能提供整体航道交通效率最优的船舶交通组织解决方案。国内外缺少针对在限制性航道条件下船舶交通组织问题的研究，但对单一类型航道(如单向、双向和复式航道)船舶交通组织问题有部分研究。文献[7]和文献[8]针对单向航道船舶进出港调度优化问题，构建单向航道船舶进出港最优序列模型；文献[9]和文献[10]考虑船舶等待时间和船型优先权等因素，建立双向通航条件下的船舶进出港数学优化模型；文献[11]、文献[12]和文献[13]研究复式航道中船舶的航行方式和交通冲突，构建船舶调度多目标数学优化模型。通过分析，单一类型航道船舶交通组织问题需考虑进出港船舶流量转换、单/双向/复式通航模式转化、船舶间安全时隙和警戒区会遇船舶协调避让等问题。相比之下，在限制性航道条件下，研究船舶交通组织问题除了要考虑单一类型航道船舶交通组织问题以外，还需考虑航道存在的限制性关键航路风险点，并识别限制性航道的限制性通航航段和单一性通航航段(单向/双向通航航段)，确保船舶在限制性通航模式与单一性通航模式之间转化时，在限制性单/双向通航模式切换时和在航道各限制性关键航路风险点航行时的安全性和效率性。在船舶交通组织优化算法方面，EDUARDO等[14]设计双向航道水域混合整数线性规划数学模型，并采用模拟退火算法进行求解。MEISEL等[15]针对双向船舶交通调度问题，提出变航速、侧线段容量和船舶等待时间限制的优化策略，采用启发式算法求解。ZHANG等[16-17]协调航道和泊位等资源构建数学优化模型，采用模拟退火和遗传算法求解。通过对船舶交通组织优化算法进行归纳发现，所采用的求解算法大都为模拟退火算法和遗传算法等常规的智能优化算法，在面对较为复杂的船舶交通组织优化问题时，常出现收敛速度慢和陷于局部最优等问题。

综上，本文在现有船舶交通组织优化理论的基础上，考虑黄骅港煤炭港区双向航道限制性条件，构建限制性双向通航模式下的船舶交通组织优化模型，并提出改进的双链量子遗传算法(Improved Double Chains Quantum Genetic Algorithm, IDCQGA)，高效地求取模型的最优方案。

1 模型建立

1.1 问题描述

目前,该港区采用先出后进(First out Last in, FoLi)方式集中调度进港或出港船舶，航道通航效率较低，实际到港船舶需先在锚地抛锚等候进港；航道最大流速出现在口门(32#浮筒)附近，对于在22#浮筒附近刚上线不久的进港空载船舶而言，其航速较慢，受风流影响较大，易给重载出港船舶造成视觉误差；航道40#浮筒附近有1个5°转向点，应避免一艘船转向给另一艘船造成视觉误差； 47#浮筒以内至一期、二期码头前沿为港池连接水域，此处富余水深略显不足，可航水域狭小，船舶操作性差；22#浮筒以外区域相距泊位较远，已无双向通航的意义。基于以上分析，归纳出影响航道通航安全和效率的限制性关键航路风险点主要包括进航道口(Key0 )、防沙堤口门(Key2)、航道5°转向点(Key3)和港池连接水域(Key4)，见图1。图1中，Key1为Key0与Key2的中点。

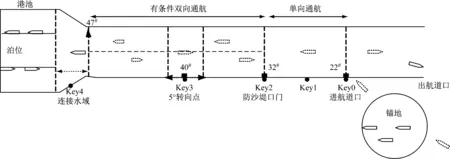
图1 黄骅港煤炭港区航道限制性双向通航示意

《黄骅港煤炭港区航道双向通航推进会纪要》对航道双向通航条件的规定：

1) 在22#浮筒附近上线处至32#浮筒口门位置航段，船舶需执行单向通航。航道32#浮筒以内区域中的外航道段(32#～40#浮筒) 和内航道段(40#～47#浮筒)船舶执行5万吨级有条件双向通航。

2) 航道同向进出港船舶前后安全距离至少保持1.5 n mile。

3) 双向通航两船暂限船长小于225.0 m，船宽不大于32.3 m。

综上，该港区限制性航道具有全局双航段异类通航(限制性单/双向通航)和局部单航段有条件通航等限制性通航的特点，从而使航道通航模式在单向/限制性通航模式间转化,在限制性单/双向通航模式间切换。单向/限制性通航模式在航道物理条件、船舶类型(船型尺度、船舶载态、船舶吃水和载运危险物等)和水文气象等因素的影响下发生转化；限制性单/双向通航模式在船舶从航道单向航段航行过渡到双向航段时切换。

考虑以上航道通航安全和效率影响因素以及船舶限制性双向通航条件，结合港方和船方在船舶进出港过程中的利益诉求，在对黄骅港煤炭港区实际船舶进出港流程进行实地调研的基础上，提炼出该港区限制性双向航道船舶交通组织优化的关键是确定最佳的船舶进出港序列，确保船舶在限制性通航和单向通航模式下以及在航道各航路风险点附近的航行安全性和效率性，缩短船舶总的调度时间和其在港的总等待时间，从而更好地提高船舶进出港作业效率。

1.2 模型假设

本文建模所需的假设条件包括：

1) 水文气象条件满足船舶进出港作业要求。

2) 引航员、拖船和锚地容量充足，不影响船舶进出港计划。

3) 船舶靠泊作业计划已提前制订，即不考虑泊位指派问题。

1.3 变量和符号定义

船舶集合N={1,2,…，n}，n为按船舶申请进出港的时间顺序确定的船舶编号；泊位集合B={1,2,…，z}，z为泊位编号。Tpi为船舶申请进出港时间，即船舶完全就绪时刻。Tsi为船舶开始被调度时刻。Tfi为船舶完成进出港时刻，对于进港船舶指船舶停靠泊位时刻，对于出港船舶指船舶出航道时刻。δ0为船舶同向安全时隙。Tgk为船舶异向安全时隙,若k=1,表示限制性双向通航单向通航阶段的平均时隙;若k∈{0,3,4},表示关键航路风险点0、3和4附近的异向安全时隙。Δtki为船舶在航道各关键航路风险点之间的航行时间，k∈{0,1,2,3,4}，其中:若k=0，对于进港船表示从锚地航行至进航道位置的时间，对于出港船表示从进航道位置航行到出航道位置的时间；若k∈{1,2,3,4}，表示进出港船舶在航路风险点k-1与k之间的航行时间。ΔBti为船舶在港池连接水域与泊位之间的航行时间。Tki为船舶航行到航道关键航路风险点k的时刻，k∈{0,1,2,3,4}。x为船舶航行方向，其中:x=1为进港；x=0为出港。y为船舶航行模式，其中:y=0为单向通航；y=r为限制性通航，r=1指限制性单向通航，r=2指限制性双向通航。Bi=1，为进港船舶i将要停靠的泊位可用；Bi=0，为进港船舶i所要停靠的泊位已被使用。A为任意一个足够大的整数。

1.4 优化模型

本文构建的在限制性双向通航模式下船舶交通组织优化模型(Ship Traffic Organization Optimization Model under Restricted Two-Way Navigation, STOOMRTWN)见式(1)～式(9)。

[STOOMRTWN]:

min:[S,W]

(1)

(2)

式(1)和式(2)中：S和W分别为第一月目标值和第二目标值。

s.t.

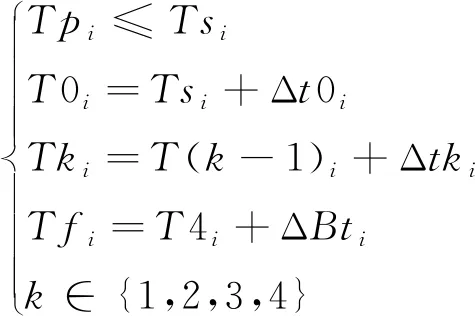
(3)

(4)

(5)

(6)

(7)

(8)

(9)

式(1)和式(2)为目标函数，分别为总船舶进出港调度时间和总船舶在港等待的最短时间；式(3)表示每艘船舶的开始调度时间不早于其申请进出港的时间，且每艘船舶调度结束时间等于其在航行过程中各关键航路风险点之间的航行时间累加，以确保船舶在航行过程中的时间连续性；式(4)～式(9)表示船舶i均在船舶j和m之后调度;式(4)为模式切换约束，用于判断当限制性通航两异向船舶切换为限制性单向通航模式时，通过调整船舶到达指定航路风险点的时刻，以保证两船在整个限制性单向航段只能保持单向航行；式(5)和式(6)为关键航路风险点交通冲突消解；式(5)表示限制性通航两异向船舶在指定关键航路风险点处保持异向安全时隙;式(6)表示进出港两船在航道单向通航模式下，各关键航路风险点处保持同向安全时隙；式(7)为泊位冲突消解，表示船舶i进港时，其所停靠的泊位必须可用；式(8)和式(9)为模式转换约束；式(8)为限制性通航模式分别转换为单向进港通航模式和单向出港通航模式;式(9)为单向进港通航模式和单向出港通航模式转换为限制性通航模式。

2 模型求解

船舶交通组织优化问题为典型的NP-hard问题[14]，采用常规精确求解工具求解较为困难，而传统的智能化算法存在收敛速度慢、易陷于局部最优等情况。鉴于此，本文基于IDCQGA的并行性、叠加性和量子位双概率幅编码等优势[18]，针对STOOMRTWN模型的特点，提出改进的IDCQGA，其主要思路如下：双链量子编码之后，对于1条染色体上的n个基因位，有2n个(-1,1)范围内的概率幅，通过将概率幅大小按升序排列，并取回原来数在排序后序列中所处的位置，将原染色体转化为整数序列，种群中每条染色体可代表所调度进出港船舶的排序情况；将量子位编码、量子旋转门和量子非门等操作与SGA(Simple Genetic Algorithm)的算子串联，最终实现1次迭代、2次种群更新和2次目标值寻优。IDCQGA的关键算子操作流程见图2。

1) 船舶交通组织双链量子编码。量子位的概率幅被用来进行编码操作，概率幅用(cost,sint)表示,其中t=2π×rand，rand为(0,1)内的一个随机数。被初始化之后的每条染色体拥有2条基因序列，即

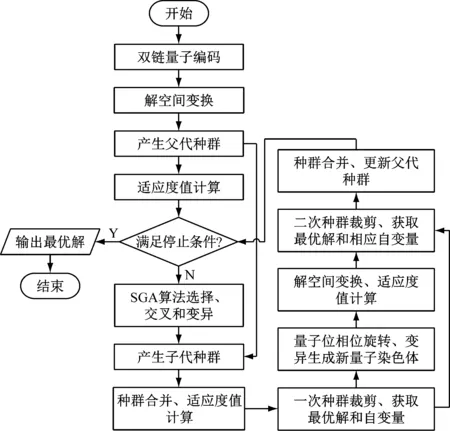
图2 IDCQGA的关键算子操作流程

picos=(costi1,costi2,…,costin)

(10)

pisin=(sinti1,sinti2,…,sintin)

(11)

式(10)和式(11)中：i∈{1,2,…,m};j∈{1,2,…,n}； 种群的大小用m表示；每条染色体量子的位数代表1个周期所要调度的进出港船舶数量n。

2) 船舶交通组织解空间变换。船舶交通组织优化问题的解空间变换发生在离散域，对于已初始化的每条染色体上的n个基因位，有2n个(-1,1)范围内的概率幅，将概率幅大小按升序排列，并取回原来数在排序后序列中所处的位置，将原染色体转化为整数序列，通过解空间转换，使产生的种群中每条染色体可代表2组被调度的进出港船舶序列，序列中每一位表示1艘进出港船舶编号。

3) 适应度函数。针对所构建模型的特点，取个体目标函数值的倒数作为适应度值，并将模型各约束条件转化为适应度函数的惩罚项。

4) SGA选择、交叉和变异。选择算子采用轮盘赌选择方法，交叉算子采用部分映射交叉方法，变异算子采取二元变异方法。

5) 量子相位旋转、变异更新染色体。利用旋转门操作更新量子比特，采用转角步长函数确定转角的方向和大小，量子变异采用量子非门操作。

3 模型与算法验证

3.1 试验数据处理

本文基于黄骅港煤炭港区获取相应的试验仿真数据，建立30艘船舶交通仿真基础数据库。设计船舶航行时间挖掘算法获取模型的关键输入参数，其中通过对港区船舶自动识别系统(Automatic Identification System,AIS)数据进行条件判断，筛选出煤炭散货船的船长、航速、吃水和经纬度位置等数据；设置航道船舶全球定位系统(Global Positioning System,GPS)位置门限，提取出航道各关键航路风险点间船舶航行时间参数；根据进出港船舶速度变化特征过滤出船舶所停靠泊位经纬度值等，并通过聚类等操作获取港池内船舶航行时间参数。船舶航行时间挖掘算法流程如下：

1) 对2018年2月黄骅港煤炭港区500多万条进出港船舶AIS暗文数据进行解码，按照itu-rm.1371协议转化为明文，并将其存储为csv格式数据。

2) 按照不同类型船舶停靠泊位位置不同、疏浚船等特殊作业船在港区航行区域比较固定等条件，筛选出进出黄骅港煤炭港区的煤炭散货船。

3) 将船舶按属性分为灵便型散货船和巴拿马型散货船，依次合理设置航道相邻关键航路风险点之间进出港船舶GPS位置门限，并分别挖掘出每个区域内每艘船舶AIS数据的时间序列，最长时间与最短时间之差即为相应关键航路风险点之间所要挖掘的时间参数。

4) 基于上述得到的AIS数据，筛选出港池内散货船AIS数据，按照进出港船船速随时间变化特征不同筛选出船舶的航行时间和其所停靠的泊位经纬度值等字段，采用k-means聚类方法，根据该港区散货船泊位数量设置聚类簇，对上述筛选出的泊位经纬度特征值聚类，并与实际泊位位置相对比得到实际泊位编号，最后计算出进港船舶航行到实际泊位或出港船离开港池的时间。

3.2 模型和算法参数设置

设置船舶调度时间从0时刻开始；基于黄骅港规定的航道船舶安全间距(使用固定距离为1.5 n mile)、第3.1节挖掘出的航道第1个单向通航航段船舶航行时间的上限值为28.4 min、航道5°弯段实际距离为1.7 n mile、码头前沿距离为1.0 n mile，按航道和港池船舶航行平均速度转换为对应的安全时隙并设定δ0为8 min，Tg0为8 min，Tg1为30 min，Tg3为9 min，Tg4为25 min；设置种群为100，量子位数为30，转角步长初值为0.01×π，交叉概率为0.95，变异概率为0.05，终止代数为300代。

3.3 仿真结果和分析

3.3.1模型求解性能和求解方案分析

采用IDCQGA和SGA对模型进行求解，重复运行50次中具有一般性和代表性的一次运行结果见图3。由图3可知：IDCQGA对模型求解出的目标值均值随迭代次数的变化较为均匀，且其第一目标值和第二目标值最优解约在100代收敛，收敛速度明显快于SGA，根据试验运行结果得到的平均质量统计对比见表1。由表1可知：IDCQGA算法下50次试验运行结果第一目标值和第二目标值最优解的平均值和标准差均明显小于SGA，表明SGA目标值每一次寻优结果的差距较大，稳定性较差，而IDCQGA算法50次试验寻优结果明显集中，稳定性较强；在算法运行时间上，IDCQGA比SGA稍长，原因是IDCQGA算法1次迭代进行2次寻优计算；综合比较得出IDCQGA算法在解决船舶交通组织优化问题中具有收敛快、解的质量高等优点。

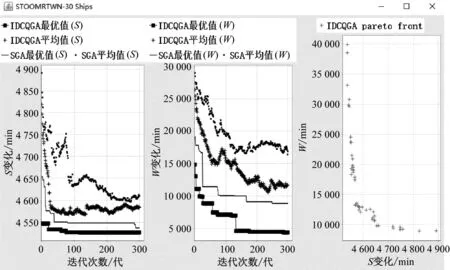
a) S随迭代次数变化 b) W随迭代次数变化 c) IDCQGA帕累托前沿面

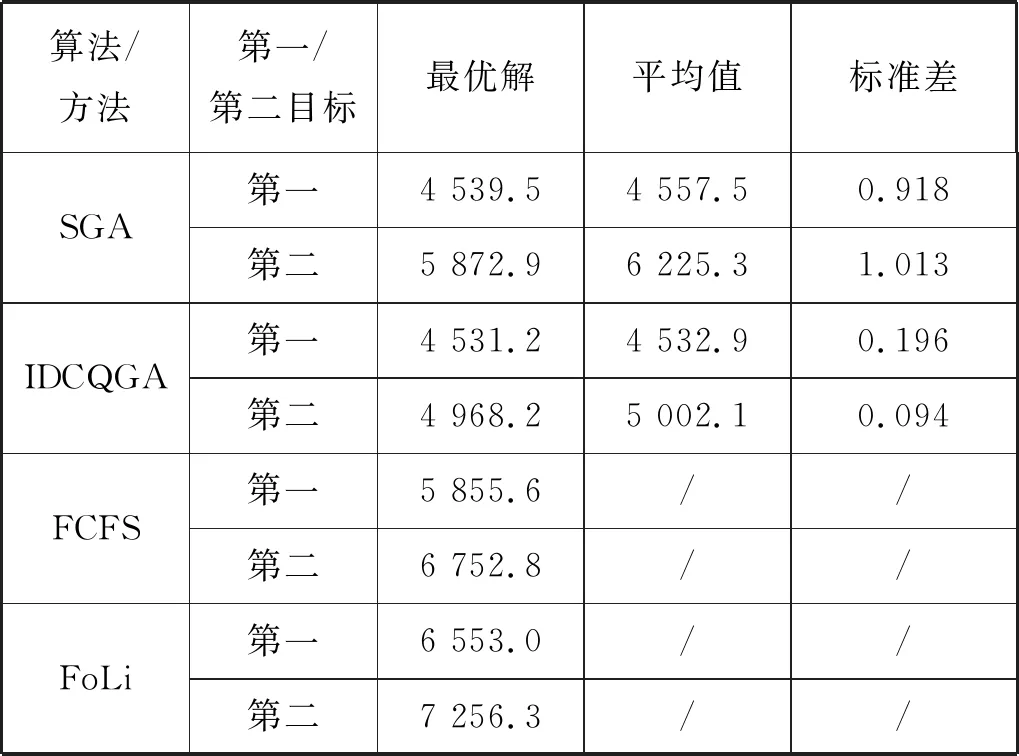
表1 根据试验运行结果得到的平均质量统计对比 min

模型求解出的Pareto最优解集中的每个最优解均代表一种优化方案。在实际应用中:若港口期望总调度时间最短，可选用第一目标值最优的优化方案；若需特别考虑船舶在港等待时间最短，可选用第二目标值较小的优化方案。为验证模型求解方案的高效性，将IDCQGA算法求解出的Pareto最优解集中第一目标最优下的船舶进出港优化方案与该港区规定的在限制性双向通航条件下船舶交通组织相关部门常采用的先到先服务(First Come First Served，FCFS)和FoLi调度策略相比较，其中船舶进出港序列为FCFS(0-29)和FoLi (0, 2, 3, 4, 5, 8, 9, 12, 19, 20, 21, 28, 29, 1, 6, 7, 10,11,13, 14, 15, 16, 17, 18, 22, 23, 24, 25, 26, 27)。

FCFS方法和FoLi方法的总船舶调度时间和总船舶等待时间最优解如表1所示。通过比较可知，IDCQGA算法的总船舶调度时间和总船舶等待时间最优解分别比FCFS方法下降22.6%和30.8%，比FoLi方法下降26.3%和31.5%，这表明采用IDCQGA算法求解出模型优化方案具有高效性。

3.3.2模型验证

对模型的验证主要是分析IDCQGA，求解出船舶交通组织优化方案见表2。表2为Pareto最优解集中第一目标最优方案的前20条船舶信息。

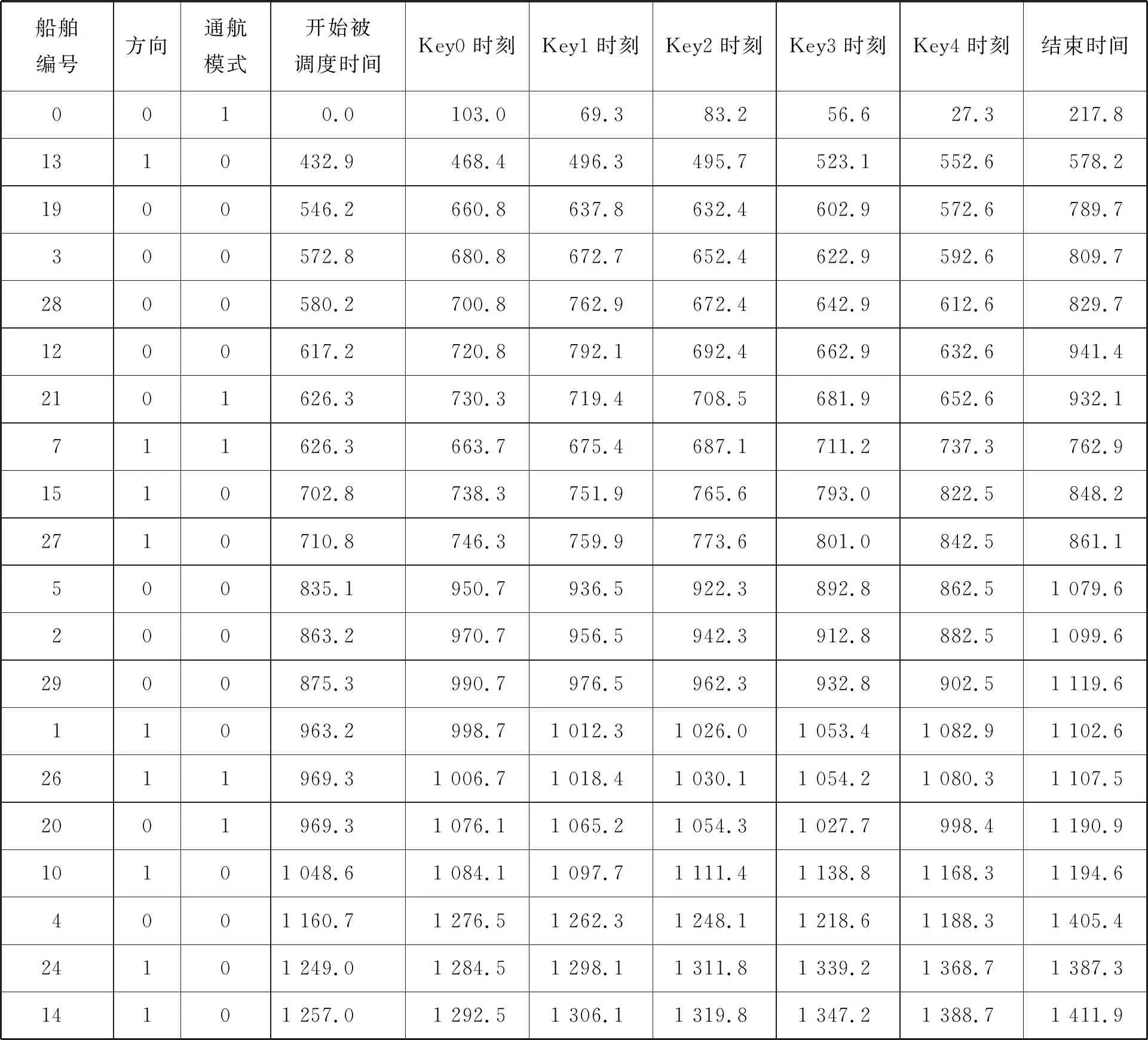
表2 船舶交通组织优化方案 min

(1) 通航模式转换验证：12#出港船舶载重吨大于5万dWT，被安排为单向通航，下一艘21#出港船舶的载重吨小于5万dWT，被安排为限制性双向通航，单向出港转化为限制性双向出港，两船在关键航路风险点4保持预设的至少8 min港池同向安全时隙；21#出港船舶和7#进港船舶的载重吨小于5万dWT，均被安排为限制性双向通航，下一艘15#进港船舶的载重吨大于5万dWT，被安排为单向通航，这时限制性通航转化为单向通航，且15#船舶与21#船舶和7#船舶在关键航路风险点0位置保持预设的至少8 min港池异向安全时隙；最后，经验证其他船的通航模式转换约束也能得到保证。

(2) 其他模型约束验证：3#出港船舶和10#进港船舶的载重吨大于5万dWT，均被安排为单向通航，而2艘船所停靠泊位相同，根据泊位冲突消解约束3#出港船舶被调度时间早于10#进港船舶，且两船各自被调度总时间等于其在航道各关键航路风险点和港池航行时间的总和；21#出港船舶和7#进港船舶的载重吨小于5万dWT，均被安排为限制性双向通航，且两船开始被调度时间均晚于其申请进出港时间，同时,两船在关键航路风险点1、3和4分别保持至少30 min、9 min和25 min的安全时隙，从而保证限制性通航2艘异向船切换到限制性单向通航后的整个限制性单向航段(Key0与Key2之间)只能保持单向航行，并消解限制性通航2艘异向船舶在关键航路风险点3和4附近的交通冲突消解；15#和27#进港船舶载重吨大于5万dWT，均被安排为单向通航，两船开始被调度时间均晚于其申请进港时间，且两船在航道关键航路风险点0～4各位置保持至少8 min的同向安全时隙；最后，经验证其他模型约束也能得到保证。

4 结束语

本文考虑黄骅港煤炭港区影响航道通航安全和效率的因素，构建限制性双向通航模式下的船舶交通组织优化模型，并设计船舶航行时间挖掘算法；提出改进的IDCQGA算法，实现双链量子编码、量子旋转门和量子非门等操作与SGA之间的耦合，快速高效地求取船舶进出港优化方案。试验结果表明：提出的限制性双向航道船舶交通组织优化方法合理、有效，能保证在船舶安全航行的前提下有效提高船舶的进出港作业效率。然而，港口船舶交通组织问题涉及面较广，本文主要研究限制性双向通航进出港船舶在航道航行的安全性和效率性、船舶停靠泊位冲突等问题，理论成果可为进一步协调港口航道、泊位、拖船、引航和锚地等众多资源，构建更为复杂、更贴近实际情况的港口限制性航道船舶交通组织优化模型奠定基础。