基于低秩分解的织物疵点检测

杨恩君， 廖义辉， 刘安东， 俞 立

(浙江工业大学 信息工程学院， 浙江 杭州 310023)

织物的瑕疵点检测是生产流程中的关键步骤，传统人工检测由于工人的视觉疲劳，往往容易造成疵点的误检和漏检[2]。相比于人工检测，机器检测则是通过软件分析采集到的织物图像来标识疵点区，其检测标准更客观，且不存在人工视觉疲劳问题，从而可有效地提高疵点检出率和检测速度。然而，由于织物背景纹理各不相同，疵点类型多种多样，如何准确区分织物的正常纹理和疵点是实现机器检测的关键。

针对疵点检测问题，常见的方法有：统计学方法、频域变换法、基于模型的方法、图像分解法等。然而，统计学方法[3-5]只适用于简单纹理，其应用范围有限。频域变换法[6-8]的检测效果依赖于滤波器的选择，在复杂纹理结构上表现不佳。基于模型的方法[9-11]建模过程复杂，计算量大。图像分解法是将原图像分解为背景和疵点，其适用范围比统计学方法广，同时计算量比基于模型的方法小，如相对全变分方法[12]、形态学成分分析[13-14]、残余共振奇异值法(RRSVD)[15]。由于织物图案具有周期性，且疵点区一般较小，因此织物的背景纹理和疵点分别具有低秩性和稀疏性。上述图像分解方法虽将织物图像分解为背景和疵点两部分；但未考虑织物纹理特有的低秩性和稀疏性，因此对于复杂周期性纹理的织物可能会出现完全无法识别疵点的情况。

低秩分解方法[16-17]是从低秩和稀疏属性出发对织物图像进行分解的一种方法，故比上述图像分解方法更契合图案纹理织物的疵点检测。文献[18]通过对织物图的Gabor与方向梯度直方图(HOG)组合特征矩阵进行低秩分解实现了疵点检测，但由于Gabor不同特征分量间存在冗余，导致检测效率较低。文献[19]用Frobenius范数代替传统低秩分解中的核范数，提高了检测速度，但由于Frobenius范数无法精确描述矩阵的低秩特性，因此检测精度有所下降。文献[20]利用先验信息图引导低秩分解，提高了检出率；但传统低秩分解的核范数在低秩逼近时存在局限性，且存在织物弹性导致的歪斜问题，因此分割出的疵点图带有许多干扰。

本文针对织物的疵点检测问题，提出了一种基于改进的低秩分解方法。传统低秩分解方法用核范数近似描述矩阵的秩，但这种近似存在较大误差，为了提高近似精确度，本文采用Beta范数进行改进，解决了由近似不精确引起的图像信息过度丢失问题。为了抑制织物弹性引起的歪斜干扰，在改进低秩分解方法的基础上，通过织物图的方向梯度直方图特征构造后验信息图，对低秩分解得到的稀疏分量进行加权处理，仿真验证了本文所提算法的有效性。

1 基于低秩分解的疵点检测算法

本文方法的流程图如图1所示。主要包含以下3个步骤：构建先验信息图，基于低秩分解的显著图，疵点分割。

图1 本文方法流程图Fig.1 Flow chart of proposed method

1.1 先验信息图构造

低秩分解虽契合织物纹理与疵点的特性，但对于复杂的织物纹理和疵点，往往需要借助特征提取。目前，大多数文献先进行特征提取，再对提取出的特征矩阵进行低秩分解[17-18]，进一步分割疵点。由于低秩分解以特征矩阵为基础，检测效果较大程度取决于特征提取，而提取出适用于所有织物纹理和疵点的特征几乎是不可能的，因此对特征矩阵进行低秩分解的做法具有一定局限性，同时没有让低秩分解方法的效果最大化。

本文以低秩分解为主体，将织物图像的特征作为先验信息辅助分解。先验信息图的具体构造过程如下。

1)
图像分块。将检测图像P进行重叠式滑窗分割，分为m×n大小的图像块Pi，相邻2个滑窗重叠区大小为(m/2)×(n/2)，得到N个图像块。

2) 对每个图像块提取基元特征[21]向量fi，并利用向量2范数计算各图像块的相对数值：

3) 根据图像块滑窗覆盖情况，统计各像素点对应的数值，即可得到先验信息图，每个像素点的值表示该点为疵点的概率大小。

1.2 基于低秩分解的显著图

由于织物背景纹理的重复性和疵点的稀疏性，可将低秩分解分割织物疵点的过程描述为以下优化问题：

(1)

式中：L和S分别为织物图像P的背景纹理和疵点部分，且满足P=L+S；rank(·)为矩阵的秩，‖·‖0为矩阵的L0范数；λ为平衡常数。一般文献在处理该问题时，采用最优凸近似理论[22]，分别用矩阵核范数和矩阵L1范数代替式(1) 中的秩函数和L0范数。

然而，在描述实际织物图像低秩特性时，由于核范数对不同大小的奇异值采用相同的收缩力度，导致图像的重要信息过度丢失，因此，本文采用Beta范数‖L‖β代替核范数，对不同的奇异值施加不同的权重，具体形式如下：

(2)

式中：σi为矩阵L的奇异值；β取0.001。

此外，实际疵点往往具有结构化分布特征，而传统低秩分解方法用L1范数描述稀疏属性时假设每个元素是独立分布的，由此得到的疵点图中往往包含部分背景纹理，因此将1.1节中构造的先验信息图作为稀疏项的权重矩阵，引导低秩分解。通过引入实际疵点的先验信息，进一步提升算法描述疵点稀疏属性的能力。同时，由于光照、阴影会导致织物图中存在高斯噪声，因此存在高斯噪声情况下的模型可描述为

(3)

通过引入拉格朗日乘子Y，利用增广拉格朗日乘子法将模型式(3)改写为如下形式：

(4)

式中：<·>表示内积；参数η>0。

由于模型式(4) 中有5个变量，为此采用交替方向乘子法，分别给出L、S、F、Y、η的迭代表达式。其中，寻找最优L时采用文献[23]提出的基于奇异值梯度的迭代方法。具体过程如下。

步骤1：设定最大迭代次数T，当前迭代数t=0，允许误差ε，并初始化L0、S0、F0、Y0、η0。

步骤2：利用文献[23]中基于奇异值梯度的迭代方法更新第t+1次的迭代值Lt+1。

步骤3：在更新St+1时，将Lt+1、Ft、Yt、ηt看作常量，并对S求导寻最值可得：

(5)

同理可得Ft+1的更新公式：

(6)

式中，G=P-Lt+1-Ft+Yt/ηt。

步骤4：根据增广拉格朗日乘子法，Yt+1和ηt+1的更新公式分别为

Yt+1=Yt+ηt(P-Lt+1-St+1-Ft+1)

(7)

ηt+1=ρηt

(8)

式中，ρ为常数。

步骤5：判断迭代是否结束。若满足t=T或‖P-Lt+1-St+1-Ft+1‖F/‖P‖F>ε，则结束迭代，并输出S；否则跳转至步骤2)，且t=t+1。

1.3 疵点分割

经过低秩分解得到的稀疏分量S中包含织物疵点信息，但对于部分织物图像，仍存在一些干扰。图2示出4种不同疵点在各环节的相应图像。由图2可知，低秩分解得到的稀疏分量S中包含较强的干扰。虽然模型式(3) 的最小化目标中加入了高斯噪声项，去除了织物图中的高斯噪声；但由于稀疏分量中的干扰不是由高斯噪声引起，因此，无法通过算法求解将其去除。

图2 后验信息图和显著图Fig.2 Posterior map and saliency map. (a) Segmentation result of broken end; (b) Segmentation result of netting multiple; (c) Segmentation result of hole;(d) Segmentation result of oil

事实上，由于织物具有一定的弹性，且生产线上的机器对织物有一定拉扯，会导致织物发生细微形变，这些形变是可恢复的。若设备采集图像的瞬间正好记录下形变的织物，则某些直线纹理在图像中呈现出来变成了有高有低、有左有右的曲线，导致图像中反映出来的矩阵秩比真实情况大。而低秩分解方法以矩阵的秩最小为其中一个优化指标，当指标达到最优时输出检测结果，显然此时包含歪斜干扰，因此，需要对低秩分解后的稀疏分量进行干扰抑制。

针对上述问题，本文通过提取织物图的HOG特征构造后验信息图，并利用后验信息图和稀疏分量构造显著图抑制干扰。具体过程如下。

1) 对图像进行重叠滑窗分块，再对每个图像块提取HOG特征向量，最后将各重叠图像块的相应数值分别对应到每个像素点，由此构造后验信息图。

2) 利用后验信息图对低秩分解得到的稀疏分量矩阵S进行哈达玛乘积得到显著图。在S和后验信息图中，像素点为疵点的概率越大则该点的数值越大。由于构造后验信息图的过程与秩无关，因此后验信息图中不存在歪斜干扰。虽然S中歪斜干扰像素点的数值较大，但在后验信息图对应位置的数值则较小；而真实疵点在S和后验信息图中均有较大数值，因此，其哈达玛乘积值远超歪斜干扰像素点。相对而言，在显著图中真实疵点比其他像素点更亮，歪斜干扰像素点则被淡化，从而抑制织物弹性引起的干扰。

3) 利用最优阈值分割算法分割显著图，得到疵点检测结果。

2 仿真结果与分析

本文使用香港大学的印花织物图像数据集(FID)，包含星型、方格型、圆点型等3种不同的纹理，其中星型有25张疵点图和25张参考图(正常纹理)，方格型有26张疵点图和30张参考图，圆点型有30张疵点图和30张参考图，每张疵点图都有其对应的疵点标定图。本文仿真均在Intel(R) Core(TM) i5-6200U 2.3GHZ CPU、4 GB内存环境下进行，使用MatLab 2018b软件实现。经多次试验，本文参数设置如下。最大迭代次数T=500，允许误差ε=10-2，增广拉格朗日参数初始值Y0=0,η0=1×10-6，低秩分解3个分量的初始值L0=S0=F0=0，常数ρ=1.1。

为了验证所提算法的有效性，本文从检测效果和检测时间两方面，分别和RRSVD方法[15]、GHOG-RPCA方法[18]、PG-LSR方法[19]、PN-RPCA方法[20]进行比较。

2.1 检测效果对比

图3示出5种算法对FID数据集的部分星型纹理织物的检测结果。

图3 星型纹理检测结果Fig.3 Detection results for star-patterned fabric image. (a) Fabric image; (b) Method of reference [15];(c) Method of reference [18]; (d) Method of reference [19]; (e) Method of reference [20]; (f) Method of this paper; (g) Ground-truth

由于星型纹理的重复单元较小，因此在相同面积下，其纹理单元的排列比FID数据集中其他2种纹理更密集。当星型纹理织物的瑕疵区很细微时，易发生漏检甚至完全检测不出瑕疵区的情况，因此本文选择数据集中瑕疵区较小的织物图进行效果对比。其中，文献[15]的方法未能很好地将疵点区和正常纹理有效分离，这可能是星型纹理单元排列过于密集导致的，如图3(b)中星型断头、星型多断头和星型破洞；对于某些细微的疵点甚至完全失效，如图3(b)中星型多破洞。文献[18]的方法能较好地检测出疵点，但其分割出的疵点轮廓明显大于实际轮廓，因此其在轮廓细节刻画方面还有待改进。文献[19]方法能较好地标识出疵点的位置，如图3(d)中星型断头和星型破洞；但其存在漏检情况，未能标记出疵点的全部区域，如图3(d)中星型多破洞所示，文献[19]方法只标注出了2个疵点区中的1个。文献[20]方法较好地检测出了疵点，且其轮廓比前3种方法更接近疵点标定图，如图3(e)中星型断头和星型多破洞；但结果中包含歪斜干扰，如图3(e)中星型断头、星型破洞和星型多网。本文算法可以较好地检测出疵点区位置，且疵点轮廓与疵点标定图相近，如图3(f)中星型断头和星型多破洞；同时基本消除了文献[20]结果中的歪斜干扰，如图3(f)中星型断头、星型破洞和星型多网。

图4示出5种算法对方格型纹理的检测结果。

图4 方格型纹理检测结果Fig.4 Detection results for box-patterned fabric image.(a) Fabric image; (b) Method of reference [15]; (c) Method of reference [18]; (d) Method of reference [19]; (e) Method of reference [20]; (f) Method of this paper; (g) Ground-truth

其中文献[15]方法对于方格型纹理织物的检测效果比星型纹理稍好，如图4(b)中的方格断头(纵)、断头(横)和方格油污，可以在一定程度上识别出疵点位置，但不能很好地将其与背景分离。文献[18]基本可以检测出大致的疵点区，效果明显优于文献[15]，但引入了一些细微噪声，如图4(c)中方格细纬。文献[19]出现了大量虚警现象，将大量背景识别为瑕疵区域，如图4(d)中方格断头(横)和方格破洞，这是由于其采用的Frobenius范数不能很好地近似矩阵的秩。文献[20]方法检测出的疵点轮廓比前3种方法更精准、细腻，但有很多歪斜干扰，如图4(e)中方格断头(横)和方格破洞。本文算法基本对每张织物图都实现了疵点区与背景纹理的分离，且没有文献[20]中的歪斜干扰，如图4(f)中方格断头(横)和方格破洞，但本文算法在图4(f)方格断头(纵)的检测效果比文献[20]稍差。

对于圆点型纹理织物，本文方法同样可以有效抑制歪斜干扰，同时对疵点的轮廓细节描述较其他4种算法更细腻。

2.2 检测时间对比

衡量算法优劣的另一个指标是检测时间。为此将以上几种方法在统一仿真环境下进行对比，其中文献[18]、文献[19]、文献[20]等方法的相关MatLab代码均由论文作者提供。由于文献[18]对每张疵点图的平均处理时间在8 s左右，与文献[19]、文献[20]等不在一个量级，因此该方法不参与此环节的对比。图5示出文献[15]、文献[19]、文献[20]以及本文方法处理FID数据集中每张疵点图的耗时对比。

图5 单张织物图的用时对比Fig.5 Compared results of time for single fabric image

整体上看，文献[15]耗时最久，其次是文献[19]与文献[20]，本文算法检测时间最短。为了更精准地比较各方法耗时，本文以平均耗时为衡量指标，其结果如表1所示。

表1 平均用时对比Tab.1 Compared results of average time

由表1可知，本文算法用时最短，随后依次是文献[19]、文献[20]、文献[15]，以上几种方法对单张疵点图的处理时间都在1 s以内，相差很小。当处理的疵点图数量增加时，这种差距就不可忽视，如图6所示。

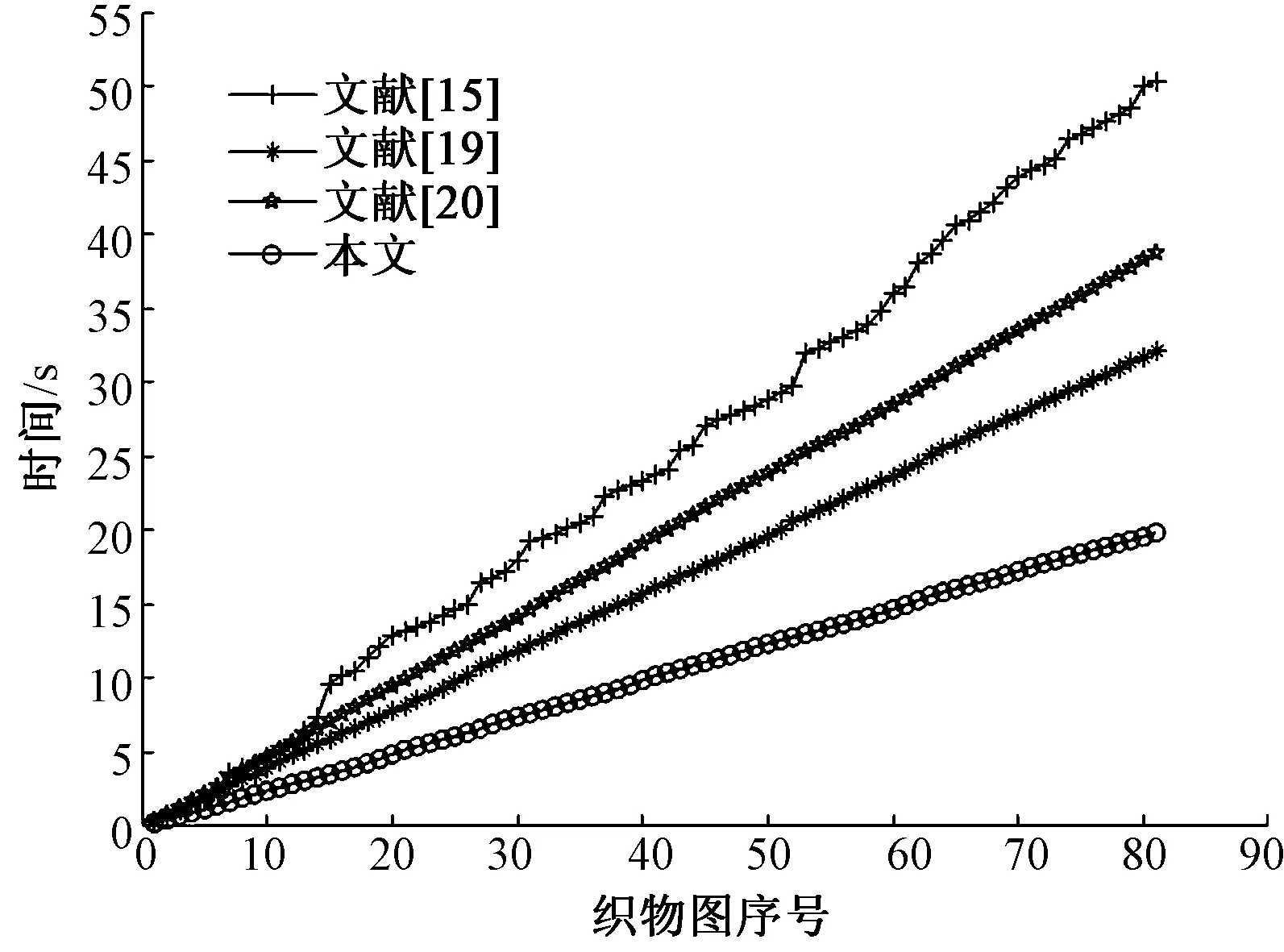
图6 FID数据集的总用时对比Fig.6 Compared results of total time for processing FID database

由图5可知，同一方法对不同疵点图的处理时间存在差异，其中一些疵点图的处理时间明显多于平均用时。这是由于该方法对此类纹理或疵点效果不佳，优化时迟迟达不到目标的误差范围。若针对不同的疵点图，检测时间有较大波动，则表明该方法稳定性不够好，适用范围有限，很难推广到其他纹理的织物检测，因此，从图5中不仅可得到每种方法检测时间的对比情况，还可分析出各方法的稳定性。

本文以标准差作为衡量各方法稳定性的指标，结果如表2所示。可以看出，稳定性从弱到强分别是文献[15]、文献[19]、文献[20]、本文算法。其中文献[20]与本文算法的稳定性相差不多，这与图5中曲线变化反映的情况一致，同时也说明了本文算法具有较好的适应性和推广性。

表2 算法稳定性对比Tab.2 Compared results of algorithms stability

3 结束语

为了解决传统低秩分解方法中采用核范数近似矩阵秩导致的图像信息过度丢失问题，采用更精准且计算量更小的Beta范数代替核范数，在解决图像信息过度丢失问题的同时，提高了算法的检测速度；利用织物图的HOG特征构造后验信息图，对低秩分解的疵点显著图进行修正，解决了织物弹性引起的歪斜问题；最后通过仿真分析验证了本文方法的有效性和适用性。下一步研究的方向主要着眼于直接从低秩分解模型本身入手，使模型变“软”，可以容忍正常范围内的织物变形，无需后验信息图即可解决织物弹性导致的歪斜问题，进一步提高检测效率。