纺织品色彩管理色表测量数据的误差优化
2021-01-05应双双裘柯槟郭宇飞
应双双, 裘柯槟, 郭宇飞, 周 赳, 周 华
(浙江理工大学 先进纺织材料与制备技术教育部重点实验室, 浙江 杭州 310018)
在纺织面料数码印花颜色加工中,不同的输入设备、显示设备和输出设备具有不同的色彩处理能力和色彩表现特性[1],色彩在不同设备间的传递过程中经常得不到准确复制。为解决颜色传递过程中色彩再现的问题,色彩管理技术应运而生[2]。目前,国际上广泛使用的是国际色彩联盟(ICC)的色彩管理规范。ICC Profile是ICC定义的规范化的色彩特性文件[3],用来表征设备的色域特性,是色彩管理技术实施的核心。色彩管理中创建ICC Profile的流程为:生成数码印花机CMYK颜色空间各通道数据组合的色表;用数码印花机打印色表;用测色仪测量色表,得到色表中CMYK各种组合的CIELab数据;通过特性化软件,建立设备相关颜色空间(CMYK)与设备无关颜色空间(CIELab)映射关系模型[4],形成一个设备的色彩特性文件。该文件完全以数据的形式表现设备的呈色特性和色域范围,即ICC Profile。由此可见,ICC Profile的建立是基于测量数据的,而测量数据的准确性决定了ICC Profile的精度。
对于纺织品数码印花等高精度颜色复制加工来说,传统的CMYK四色墨水已不能满足要求,实际数码印花中常采用6~8色多通道墨水打印[5],设备颜色空间也相应地由3维(RGB)、4维(CMYK)增加到N维(N>4)。随着颜色空间维度的增加,各通道数据组合数大大增加,导致测量的样本数据量剧增。纺织面料不同于纸张,其表面粗糙且柔软易扭曲变形,现有的自动扫描测色方法无法准确定位色块,所以目前以手工测量为主,但每个人的操作方法、习惯和手势都不同,这会使测量结果因人而异。研究[6]表明:在相同条件下,同一块打印面料由同一个人在不同时间段测量,或者由不同人分别测量,测量结果都存在差异,这表明了测量误差客观存在。
测量误差会引起呈色规律出现跳变和反演,使生成的ICC Profile输出的颜色误差大、明暗跳变严重,产生色疤、敏感色等问题。这些测量误差是随机无规律的,如何对不知真值的颜色测量数据进行优化成为亟待解决的问题,现有的色彩管理工具i1 Profiler、ProfileMaker对测量误差的优化效果差强人意。为此,本文提出一种基于多方向的曲线拟合算法,旨在有效降低测量数据误差过大、呈色规律反演带来的影响,建立颜色转换精度更高、更稳定的ICC Profile。
1 传统数据优化方法
在纺织品数码印花实际生产过程中,按照色彩管理流程对打印出来的色表进行测量后,由于人为无法判断得到的测量数据哪些是正常值,哪些是存在误差的数值,通常采用多次测量取平均值的方法来减小误差[7]。但对于多通道数码印花来说,因样本量巨大,大样本的手工重复测量耗时费力,成本很高。
在实际生产中可以发现,在多通道设备颜色空间中,如果只有单一通道数据按比例变化,其他通道保持不变,即在设备颜色空间中形成一条符合线性关系的线段,将该线段映射到测量CIELab中,根据呈色规律会形成一条连续平滑的曲线,因此,在有误差的情况下,用平滑的拟合曲线上的点来代替测量点,该点可能是在满足呈色规律下的更优点。基于此现象,可通过曲线拟合方法来检测和降低测量误差带来的影响。
曲线拟合是用连续曲线近似地刻画平面上离散点组,表示坐标之间的函数关系的一种数据处理方法,可拟合出一条与实际测量点的误差最小的光滑曲线。图1示出使用MatLab模拟的曲线拟合示意图。
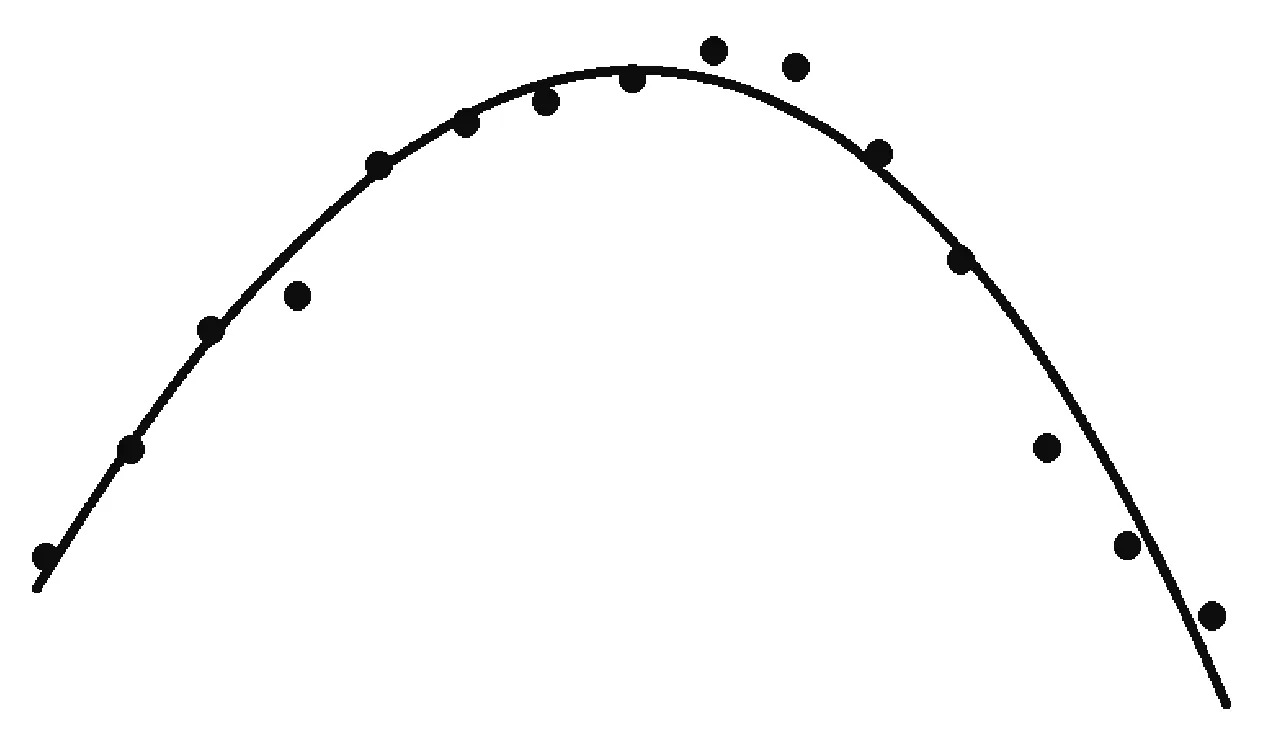
图1 曲线拟合示意图Fig.1 Example for curve fitting
最小二乘法是最常用的曲线拟合方法,其基本原理[8]如下:求一个函数y=f*(x)对所给数据点集{(xi,yi),i=0,1,…,m}拟合(m为所给数据点个数),记误差ei=f*(xi)-yi(i=0,1,…,m),误差集E=(e0,e1,…,em)T, 设φ0(x),φ1(x),…,φn(x)是C[a,b]上的线性无关函数族(n为函数个数),在函数空间φ=span{φ0(x),φ1(x),…,φn(x)}中找到一个函数f*(x),使误差平方和为
(1)
其中,
f(x)=a0φ0(x)+a1φ1(x)+…+anφn(x) (n (2) 用最小二乘法求拟合曲线时,首先要根据所给数据的运动规律确定f(x)的形式。f(x)的一般表达式为式(2)表示的线性形式,若φk(x)是k次多项式,f(x)就是n次多项式。对于本文提及的色表测量数据来说,f(x)可采用二次多项式、样条函数等形式。 以实际数据与拟合曲线的误差的平方和最小为原理,本文将测量数据用最小二乘法拟合成连续的三维曲线[9],用该法求得的曲线可最大可能地逼近测量数据集,反映出测量数据的整体分布趋势。然而所有的测量点都可能存在误差,单一方向的曲线拟合效果并不佳,甚至有可能增大误差,不能满足应用需求,因此,本文提出一种在三维颜色测量空间中,对每个测量点用过该点的多个方向曲线拟合来进行优化的方法。 根据假设,取多通道设备颜色空间A中任一色靶点Aj,在多维设备颜色空间A中枚举出所有过Aj的线段,然后在三维测量颜色空间B中,判断上述每条线段上Aj的对应测量点Bj是否落在某一连续平滑的曲线上,以此来判断色靶点的测量数据是否误差过大。而在二维及以上空间中,过一点可找出多条线段,如对一个等间隔的三维空间,至少存在有13条过中心点的符合线性关系的线段。图2 示出空间中过一点的直线示意图。 图2 空间中过一点的直线示意图Fig.2 Schematic diagram of all lines passing through one point in space. (a) Cube space;(b) Plan view; (c) Overall diagram 如图2所示,在立方体空间中,从X-Y、X-Z、Y-Z平面俯视图以一点为间隔分别可找到4条过立方体中心O点的线段,其中有3条重复。将立方体的对角线相连,也可找到4条符合条件的线段,所以共计13条线段。在此基础上,若是以2点为间隔或是在不等间隔情况下寻找空间中过一点的线段,那么将会有无穷多条,因此,这些颜色线段映射到测量颜色空间后,测量数据将会在Lab测量颜色空间以不同方向的光滑曲线存在,如图3所示。 图3 Lab颜色测量空间Fig.3 Measurement data in Lab space 从图3可以看出,在测量颜色空间中,有不同方向的多条拟合曲线,在每条曲线上都存在测量数据的拟合点B′j。方向数可根据测量数据具体情况具体分析,但都至少有3个方向。理论上当测量数据没有误差的情况下,这些点应该重合为一点。由于误差客观存在,转而求误差最小点,一般来说这些点的重心就是误差最小点,但每条拟合曲线的线段质量不同,那么曲线上的拟合点对最终的优化点的影响程度也将不同,因此,需要分析曲线的线段质量,计算线段的权重系数来求误差最小点即最终优化值。 对每条拟合曲线的线段计算其权重系数,权重系数大小作为该曲线线段质量的判定依据。一般地,计算线段的权重系数Wj方法如下:求出测量数据所在切平面P的法向量Vj,并求出该线段上其他测量数据切平面的法向量Vn。然后,求出法向量Vj与其他法向量Vn的夹角,设夹角范围为[0°,180°],则权重系数为 (3) 夹角反映出测量数据在该方向的偏向:90°以内,夹角越小表明测量数据在该方向上的偏向越小,误差也越小,相应的权重系数则越大。根据向量积右手法则来判断一个平面法向量的方向,如图4所示。图4(a)中叉号表示在同一平面内的测量数据所在切平面的法向量方向都为垂直纸面向内,则该情况下法向量之间的夹角为0°;图4(b)中空心圆表示法向量垂直纸面向外,此时,测量数据4所在的切平面的法向量与其他法向量呈180°夹角。在三维空间,测量数据分布在不同平面上时,上述法向量之间的夹角会在0°~180°内变化,如图4(c)、(d)所示,可根据式(3)计算相应权重系数。 图4 权重系数计算示意图Fig.4 Calculation of weight coefficient. (a) Same plane with normal vector angle of 0°; (b) Same plane with normal vector angle of 180°; (c) Different plane with same biased normal vectors of angle∈[0°,90°];(d) Different plane opposite normal vectors of angle∈(90°,180°] 图5 基于多方向曲线拟合的数据优化方法效果示意图Fig.5 Effect of data optimization method based on multi-directional curve fitting. (a) Optimization of measurement data with large error; (b) Optimization of measurement data with less error (4) 式中:d表示不同方向;s为方向数。 从图5(a) 中可直观看出,该优化方法对于误差较大的测量数据具有优异的优化效果,而对于图5(b)中测量数据中误差小的部分,该优化方法对其改动很小,符合预期。 为验证该多方向曲线拟合数据优化方法的有效性,采用杭州宏华数码科技股份有限公司自主开发的软打样软件ATSoftProof[10],结合主观评价方法和客观评价方法,对数据优化前后生成的ICC Profile进行质量评估。 客观评价选用软打样软件ATSoftProof中的“ICC评估”工具[11],对打印机ICC Profile的质量从多方面进行快速定量评估,得到量化的评估报告,通过评估报告里的客观数据来评价ICC Profile的质量。 实验织物:1.5 m×2.0 m色丁(经纬纱线密度均为 5.6 tex)。实验墨水:CSK00 012分散墨水。实验仪器:MODEL X型高速热升华数码印花机。测色仪器:X-Rite i1 Basic Pro2型分光光度计。以上实验环境均由杭州宏华数码科技股份有限公司提供。随机选取25组该公司目前应用较多的ICC Profile及其相关原始测量数据,采用本文的多方向曲线拟合的数据优化方法对测量数据进行优化,再生成优化后的ICC Profile。将优化前后的ICC Profile导入ATSoftProof软件中进行质量评估,色差公式选择CIEDE2000(2∶1∶1)。评估报告主要给出优化前后ICC的整体平均色差、难打色平均色差、中性灰色平均色差等相关数据。其中,难打色主要指的是一些深的高饱和颜色,数码印花机在打印这些颜色时,呈色性能不及传统印刷机,导致最终颜色不丰富,色域小,波动大;在色相和彩度没有变化的前提下,只有明度变化的颜色为中性灰色,人眼对此颜色非常敏感,当测量数据存在误差时,生成的ICC Profile会引起输出的颜色数据产生偏差。25组ICC Profile优化前后的色差数据如表1所示。 表1 25组ICC Profile优化前后的色差Tab.1 Color difference of 25 ICC Profiles before and after optimization 表1结果表明:经本文数据优化方法优化后的25组ICC Profile整体平均色差降低了12.30%;难打色平均色差降低了16.67%;中性灰色平均色差降低了16.74%。说明优化后的ICC Profile精度更高。 主观评价在软打样软件 ATSoftProof中完成,将实验图导入ATSoftProof中,在“校样(软打样)设置”下,分别选取数据优化前后的8号ICC Profile,设置好准确的打印参数,分别生成与原图对比的色差分布图,保存图像。图像中亮暗表示色差的大小,越亮表示此处与原图比色差越大。 随机选取1组ICC Profile数据优化前后生成的色差分布图效果如图6所示。其中:图6(a)为选取原始测量数据生成的ICC Profile后显示的色差分布图;图6(b)为选取经本文误差优化方法优化后的测量数据生成的ICC Profile后显示的色差分布图。生成的色差分布图是和原图等大小的 8位灰度图,图像中每个像素都反映出该位置像素的打印色差值,0表示没有色差,数值越大表示色差越大,显示越亮。不难发现,图6(b)整体要比图6(a) 暗,通过对比图中箭头标识所在水平线上136个像素点RGB色差值变化(见图6(c)、(d)),结果表明优化后的打印色差大部分比优化前小。由此,从主观上验证了该数据优化方法有利于得到更准确的ICC Profile。 图6 ICC Profile优化前后色差分布图对比Fig.6 Color difference distribution map before and after optimization of ICC Profile.(a) Color difference distribution compared with original image before optimization; (b) Color difference distribution compared with original image after optimization; (c) Color difference value corresponding to each pixel before optimization; (d) Color difference value corresponding to each pixel after optimization 本文针对色彩管理中色表测量数据存在误差,影响后期生成ICC Profile精度的问题,提出一种基于多方向的曲线拟合算法,用于优化测量数据。对25组优化前后的ICC Profile进行质量评估,客观数据体现出优化后的ICC Profile整体平均色差减小了12.30%,主观视觉也可在一定程度上验证色差呈减小趋势;优化前后色差分布图也进一步表明该优化方法减小了颜色色差。结果证实,该多方向曲线拟合算法可有效减小色彩管理中色表测量数据误差,达到优异的数据优化效果。本文研究结果为纺织品色彩管理中建立高精度的ICC Profile,实现高保真色彩管理提供了可能,具有较好的实用性。 FZXB2 多方向曲线拟合的数据优化方法
2.1 多方向的测量数据
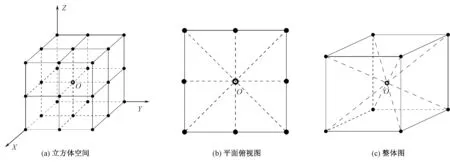

2.2 线段权重系数计算

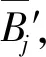

3 应用分析
3.1 客观评价

3.2 主观评价

4 结 论
