一种利用全站仪和检校场的相机/惯导空间标定方法
2021-01-05张小红
贾 俊,朱 锋,张小红,2
(1.武汉大学 测绘学院,武汉 430079;2.地球空间信息技术协同创新中心,武汉 430079)
0 引言
随着智能化时代的到来,自动驾驶和移动机器人领域蓬勃发展:如谷歌的无人驾驶汽车[1];又如配备有大量不同类型传感器的测量机器人,这些传感器用以执行环境感知和导航定位服务。多传感器融合已成为了未来发展的趋势。然而传感器的组合,首先要面临标定的问题,传统的全球定位系统(global positioning system, GPS)和惯导组合系统的标定,可以通过测量杆臂和惯导初始对准获得传感器间平移参数和旋转参数,而视觉和惯性测量装置(inertial measurement unit, IMU)间平移参数不能直接量取,旋转参数计算受限于观测条件和组合系统解算精度,目前常用的标定方法通常不能获得稳定、可靠的标定结果。
视觉传感器和惯性传感器[2]的组合具有互补的特点。通过合并来自2 个不同源的信息,可以获得鲁棒的相机位姿运动,便于视觉识别和跟踪兴趣目标。相机和惯性传感器的组合已经在增强现实(augmented reality, AR)[3]和即时定位与地图构建(simultaneous localization and mapping, SLAM)[4]等领域中得到了广泛的应用。由于相机的光学中心是随着焦距不断改变的,通常无法直接量取相机和惯导之间的杆臂。为了解决标定问题,许多学者提出了不同的解决方案:21 世纪初,文献[5]提出将相机和 IMU 安装在具有高分辨率编码器的摆上来解算相机和IMU 的旋转参数;文献[6]利用简单无源转台来标定图像解算相机和 IMU的平移参数;2007 年,文献[7]采用基于卡尔曼滤波的递归算法,同时解算相机和IMU 的旋转参数和平移参数;2011 年,文献[8]利用相机和IMU时间同步的输出,来估计传感器间的旋转参数和平移参数,这种自标定方法构成了之后标定发展的框架;2013 年,文献[9]发布了卡利布尔(Kalibr)工具箱,该工具箱可以提供多传感器间的离线标定,成为了相机和 IMU 标定的主流工具;2017年,香港科技大学团队在文斯(VINS)开源代码中,提出了在线标定方法[10],其标定结果为,平移参数优于2 cm,旋转参数优于1°。上述校准方法属于自标定的范畴。自标定需要IMU 和相机输出数据并建立复杂的数学模型,观测条件也会影响结果的准确性。此外,上述自标定方案不适用于大尺寸和杆臂较长的相机和IMU,因为惯导不能充分激励,导致结果不稳定。
为了优化上述方案,解决存在的问题,本文方案使用全站仪和标定场来简化标定过程。全站仪和标定场可以提供相机和IMU 之间的转换关系。这种相机和惯性传感器不需要移动的标定方案,适用于大型IMU 和相机组合的应用,如机器人、车载导航、机载导航等。
1 惯导/相机空间标定的原理与方法
自标定的缺点是模型复杂,不适用于大型传感器的标定;因此提出了新的解决方案:利用全站仪观测惯导的角点,利用相机匹配到标定场的3 维控制点,以世界坐标系为标定的媒介,首先构建惯导坐标系和相机坐标系在世界坐标系下的关系,进而得到惯导和相机的外参数。为了方便之后的表达,本文定义在任意时刻从,A 坐标系转换到B坐标系的变换可以表示为表示相对旋转,表示相对平移。
1.1 相机和惯导内参数标定
在标定外参数之前,首先对相机和惯导的内参数进行标定。由于惯导参数尺寸在出厂前会严格标定给出,而变焦相机其光心在没有固定焦距前是可变的,因此内参数标定主要是对相机光心位置的确定。公认的相机标定方法是使用矩阵实验室(MATLAB)[11]中的相机标定工具箱。其原理是利用单应性矩阵[12]构建3 维空间和像素平面的关系,单应性矩阵估计可表示为
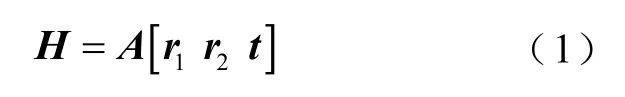
式中:H 为单应性矩阵;A 为相机的内参数矩阵;r1、 r2表示2 个平面之间的旋转矩阵;t 表示平移矩阵。通过估计标定板平面在相机镜头前不同位置处,相对于相片平面的旋转和平移,来得到单应性矩阵,进一步可以获得相机的内参数矩阵,内参数矩阵可表示为

式中:( u0, v0)为像主点坐标在像平面上的投影;fx和 fy分别为u、v 轴中的尺度因子;s 为2 个图像轴的偏度。
1.2 世界坐标系到相机坐标系的相对姿态
利用相机标定场来获取世界坐标系到相机坐标系之间的旋转和平移。本文采用 N 点透视(perspective-n-point,PNP)的方法[13],其原理是利用标定场中3 维控制点X 投影到相机像素平面u 多组同名点的映射关系,解算3×4 维度大小的投影矩阵P,映射关系可表示为
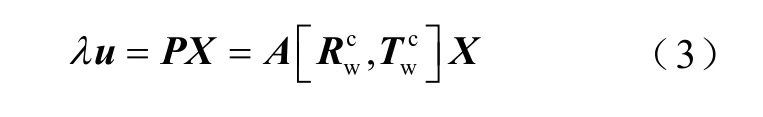
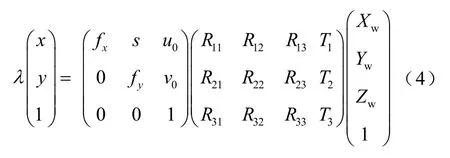
式中:( R11,…, R33)为旋转矩陈的元素;(T1,T2,T3)表示3 个轴向(前右上坐标系)的平移;Xw、Yw、Zw为在世界坐标系下控制点的坐标。矩阵表示旋转和平移,有6 个自由度,表征6 个外参数(3 个表示旋转,3 个表示平移),有3 个或3 个以上对应同名点,利用非线性最小二乘估计可以求解,求解过程可表示为:
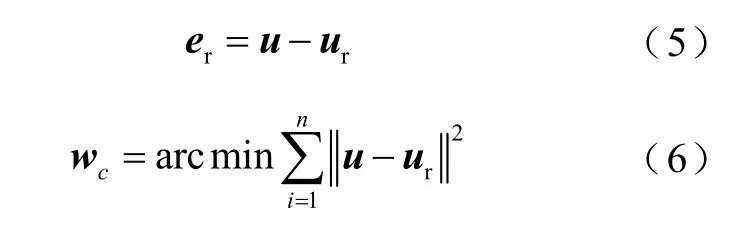
式中:er为重投影误差;ur为重投影得像素点坐标;参数向量wc为旋转和平移待求参数组成(和)。
1.3 世界坐标系到惯导坐标系的相对姿态
全站仪可以测量惯导传感器的角点在世界坐标系下的坐标。利用3 维空间变换[14]得到世界坐标系和惯导坐标系的相对姿态,空间变换可表示为

式中:(Xw,wY , Zw)为标定场中的3 维控制点坐标;(XI,IY , ZI) 为大型IMU 传感器的角点,通常为8 个角点构成1 个立方体。3×4 维度的矩阵为赫尔默特(Helmert)变换,在这2 组数据之间有6 个自由度(3 个方向和3 个平移)。由于式(7)中的等式并不是线性的,需要使用非线性最小二乘和3 个或更多的对应点来解算,可表示为:
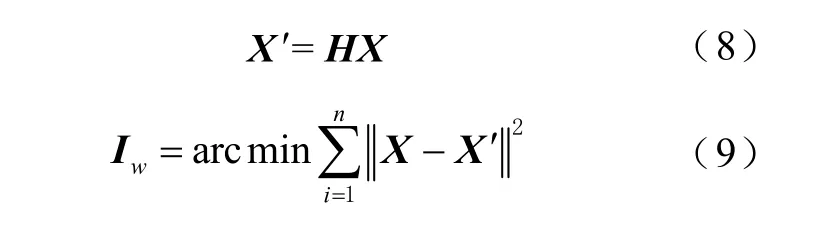
式中:H 为赫尔默特(Helmert)变换; X ′为仿射变换后的估计值;参数向量 Iw由2 个坐标系的旋转和平移参数组成()即最终得到的结果。
1.4 惯导坐标系到相机坐标系的相对姿态
结合1.3 节中的IMU 坐标系到世界坐标系的转换关系()以及1.2 节中世界到相机坐标系的转换关系(),可以进一步得到从IMU 到相机坐标系的转换关系(),旋转平移变换可表示为:

2 标定流程与精度分析方法
2.1 标定流程
第1 步,双目自标定。本文采用棋盘格玻璃板作为标定板,借助MATLAB 的双目标定工具箱,获得2 个相机的内参数和相对姿态,要求利用脉冲信号控制2 台相机,以相同频率拍摄相片;同时移动标定板,使其处于不同的位置和角度。
第2 步,全站仪测量标定场靶标点。标定场的靶标点坐标是由精密仪器测量的,为了验证其精度,本文选取了20 多个靶标点作为检核点,利用毫米级误差的全站仪进行测量,估计其误差。
第3 步,全站仪测量惯导设备角点。标定针对的是大型惯导,其角点参数在惯导坐标系下为已知。为了获得其在世界坐标系下的坐标,在惯导的角点贴上反射片,利用全站仪测得其坐标。
第4 步,相机摄像匹配靶标点。1.2 节指出,需要得到3 维控制点在相机影像中同名点的坐标。靶标点圆心为3 维控制点,且靶标点都有明确的编号。利用霍夫变换[15]提取圆心的算法,即可以得到靶标点的像素坐标,接着利用编号与对应的3 维控制点进行匹配。
第5 步,标定参数解算。按照章节1 中的原理,利用观测得到的结果进行标定参数解算。求得到旋转和平移参数后,按照内外符合精度评价结果,其中PNP 的原理已在1.2 节中进行了介绍;采用多次实验结果的标准差(standard deviation,STD)作为评价内符合精度的重要标准。标定方案的流程如图1 所示。
2.2 精度评定方法
好的标定参数结果对于多传感器融合的应用至关重要。自标定由于外部信息较少,仅通过输出结果的均值和标准差很难评定自身的精度。由于有标定场和全站仪的辅助,可有多个标定结果的评定方法。

图1 标定方案流程
评定方法1:利用已知的IMU 尺寸参数。使用全站仪和自粘反射片来测量IMU 的角点坐标。通过测量的角点解算的IMU 长、宽、高和实际传感器的长、宽、高参数进行比较,来评价全站仪的测量精度。
评定方法 2:选择标定场的靶标点作为检查点,利用全站仪测量来获取靶标点十字丝中心的3 维控制点坐标。将全站仪测得的检查点坐标与标定场预先给定的精确控制点坐标进行对比,检核标定场中控制点的精度。
评定方法4:为了更好地评定相机和惯导之间的旋转,将旋转矩阵转换为欧拉角进行分析,标准的转换顺序是Z→X→Y。标定得到左右相机与IMU传感器之间的旋转参数和平移参数后,计算结果的STD,用STD 来评价结果的稳定性。
评定方法5:利用标定结果计算标定的左右相机之间的基线长度,与用MATLAB 进行双目相机标定得到的基线长度做对比。同时也可以通过比较,直接用卷尺测量相机与IMU 之间的杆臂来验证标定平移参数的准确性。
3 实验与结果分析
3.1 实验设备条件
双目相机采用的是加拿大普安特-格雷(Point Grey)公司的 Grasshopper3U3 系列 GS3-U3-28S5M-C 的工业相机,以及FA1 英寸系列长通道HC1605A 镜头。相片的分辨率是1 920×1 200 个像素,焦距大约是16 mm,1 个像素的大小为4.54 μm。惯性传感器IMU 为加拿大诺瓦泰尔(Novatel)系列的SPAN—FSAS 高精度捷联惯导系统,它的惯导坐标系中心在它的IMU 几何中心处,尺寸参数出厂时严格标定。相机、IMU 和全站仪如图2、图3所示。

图2 双目相机和惯导

图3 实验全站仪
全站仪采用天宇CTS 型号的免棱镜全站仪,测点精度在毫米级。
标定场位于中国湖北省武汉市洪山区武汉大学测绘学院。标定场内建立了精确的坐标系,每个靶标点十字丝中心的3 维控制点坐标为已知。靶标点和相机拍摄影像如图4、图5 所示。

图4 靶标点示意图

图5 标定拍摄相片
3.2 实验结果分析
通过大量的标定实验,验证了该标定方案的可行性和可靠性。为了更好地反映此方案的准确性,对校准结果进行了评估。
第1 步,验证全站仪的测量精度。使用全站仪测量IMU 的角点,计算IMU 的长、宽、高,并将测量结果与IMU 出厂参数进行比较,评价全站仪的测量精度,如图6 所示。
通过几组实验对比,可以看出全站仪的测量精度在毫米级,与全站仪规定的测量精度一致。

图6 IMU 参数与全站仪测量结果差值
第2 步,验证全站仪标定场的控制点精度。考虑到随着时间的推移以及其他外界因素,会影响控制点的准确性,选取了20 个控制点作为检验点。将检查点测量得到的坐标与标定场给出的坐标进行比较,误差分析如图7 所示。

图7 检核点坐标与量测结果较差
从图7 可以看出,检查点与控制点坐标之间的误差在毫米级。考虑到全站仪的测量误差,可以证明控制点的坐标是可靠的。
第3 步,验证得到的相机坐标系和世界坐标系外参数的准确性。将3 维点重投影成像素坐标,并将计算出的像素坐标与观测值做比较,实验中1 个像素的大小是4.54 μm×4.54 μm,左右相机重投影误差如图8 所示。
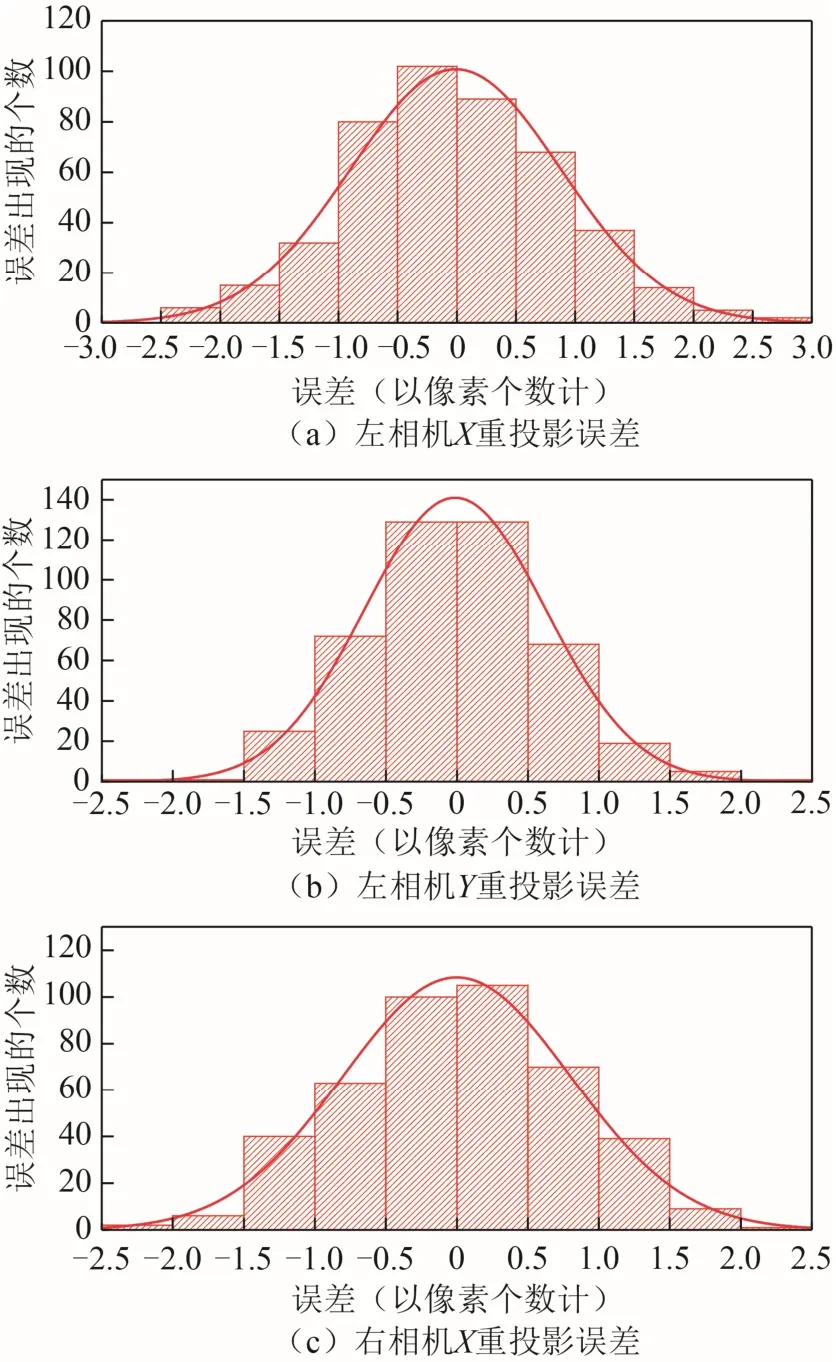
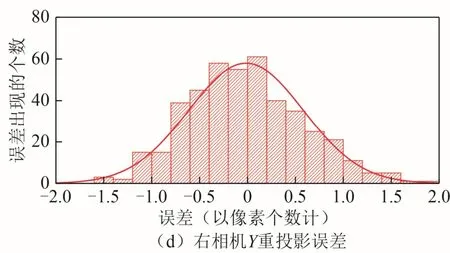
图8 重投影误差分析
从图8 可以看出,重投影的精度基本上在2 个像素以内,这证明了结果的可靠性。
第4 步,验证该标定方案结果的准确性。为了更好地表达旋转的稳定性,选择将不同组之间标定的旋转矩阵与其中1 组旋转矩阵的转置相乘并转换成欧拉角显示。这种表示方法的好处是更加直观,而且在大多数相机和惯导组合应用场景中,相机和惯导的坐标系在俯仰角上有90°的旋转,如果直接转成欧拉角,会出现万向锁的问题;而选择旋转矩阵与另1 个旋转矩阵的转置相乘,则可以很好地规避这个问题。左右相机平移参数和旋转参数标定结果如图9 所示。


图9 多次实验结果标定结果
从图9 可以看出,旋转和平移非常稳定的标定结果,旋转参数的STD 在0.5°左右,平移参数的STD 在5 mm 左右,旋转参数与自标定的结果相当,平移参数优于目前厘米级的自标定精度。
第5 步,由于相机和惯导固定在参数已知的钢板上,利用钢尺量测相机和IMU 固定点之间的杆臂作为参考值,同时比较双目相机之间的基线结果和MATLAB 的结果。为了减少参考的误差,参考值多次计算取平均,钢尺量测参考值标定精度的分析结果如表1 所示,MATLAB 参考值标定精度分析结果如表2 所示。
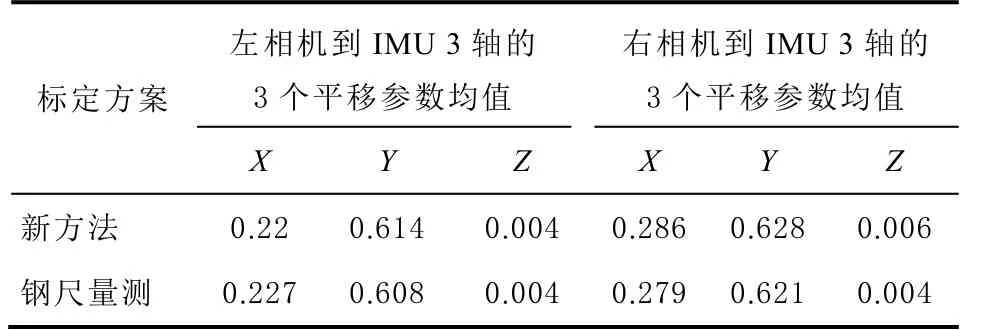
表1 钢尺量测杆臂和标定方案结果对比 单位:m
MATLAB 相机标定工具箱作为公认的标定工具,与本文标定方案的比较,可以进一步验证方案的可靠性。上述结论中,高程误差相对于平面误差较小,这是由于估计变焦相机光心时,光心在相机中的高程是固定的,因此高程方向上的误差更小。与目前常用的标定方法比较:2017 年VINS 自标定方法平移参数优于2 cm,旋转参数优于1°,而常用的Kalibr 工具箱,平移参数标定精度通常在厘米级,旋转参数标定精度优于1°;在对本次实验设备进行标定时,由于相机和惯导的杆臂过长,惯导在激励过程中受到相机位置的约束,多次标定结果不稳定。对比本文提出的标定方法,可以看到相比于自标定,借助精密外部测量仪器全站仪和标定场可以获得更好的标定结果。

表2 MATLAB 求解的基线与新标定方案的比较单位:m
4 结束语
多源传感器的发展和应用,离不开高精度的传感器外参标定结果。随着移动测量机器人和自动驾驶对定位精度要求越来越高,传感器间外参标定的好坏显得至关重要。与现在广泛使用的自标定方式不同,本文提出的标定方案借助测量仪器、无需惯导的输出,不用对大量的观测数据进行建模处理,同时规避了多传感器时间同步的问题。这种标定方法适用于大型IMU 或相机与IMU 之间杆臂过长的情况,因为在这种情况下,惯导移动不便,且移动距离由于杆臂的原因受限,不能让IMU 充分激励达到良好的标定效果。通过实验和结果分析,验证了本文提出的标定方法的准确性和可靠性。
