100 t钢包流场物理及数值模拟研究
2021-01-04郝晓倩高立福武光君刘春伟屈天鹏
郝晓倩,高立福,崔 振,武光君,刘春伟,屈天鹏
(1 山钢股份莱芜分公司,山东 济南271104;2 苏州大学沙钢钢铁学院,江苏 苏州215021)
1 前 言
钢包又称为大包,是用于盛放钢液并进行精炼和浇注的容器[1]。钢铁连铸是一个高温、不可见、复杂的冶金过程,钢包是连铸的主要容器之一,因此物理模拟和基于fluent的数值模拟在钢包流场研究中具有重要意义。
2 物理试验研究
2.1 物理试验原理
钢包中钢液的流动,是钢液在重力作用下从钢包水口流入中间包,在这种情况下,一般可视为黏性不可压缩稳态流动,同时可以忽略化学反应的影响,因此在进行流动模拟研究时,系统主要满足几何相似和动力相似[2]。
几何相似,即模型与其原型形状相同,但尺寸可以不同,而一切对应的线性尺寸成比例,这里的线性尺寸可以是直径、长度及粗糙度等。本试验中钢包模型(Lm)与实际(Lp)的几何尺寸相似比选择为1∶3[3]。
动力相似,用水作为介质模拟钢液,水和钢液的物理性质如表1 所示。因为水的运动黏度与钢液的运动黏度相当。动力相似要求模型和原型中流体的雷诺准数Re 和付鲁德准数Fr 分别相等,但是在试验过程中,同时满足模型和原型的雷诺准数Re 和付鲁德准数Fr 相等是相当困难的。根据流体力学原理,当流体流动的Re 数大于第二临界值时,流体的湍动程度及流速的分布几乎不再受雷诺数的影响,也就是说流体流动进入第二自模化区域。一般雷诺数的第二自模化区的临界值为1×104~1×105,此时,只考虑Fr 数相等,即能够满足动力相似[4]。

表1 水和钢液的物理性质
钢包底吹氩促使钢液体系流动主要作用力是气泡的浮力,而非湍流的粘滞力。考虑物理模拟试验满足模型及原型的Fr’相等,以保证模型与原型之间的动力相似。依此可以确定模型钢包中底吹气量的设计范围[5]。
相似准数Fr’定义为:
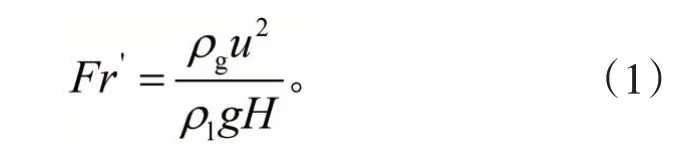
式中:u为特征速度,m/s;H为熔池深度,m;ρ1、ρg为液体和气体的密度,kg/m3;g为重力加速度,9.81 m/s2。
特征速度u可由下式给出:

式中:Q为气体体积流量,m3/h;d为底吹喷嘴直径,m。联立上式,由Frm’=Frp’可得:
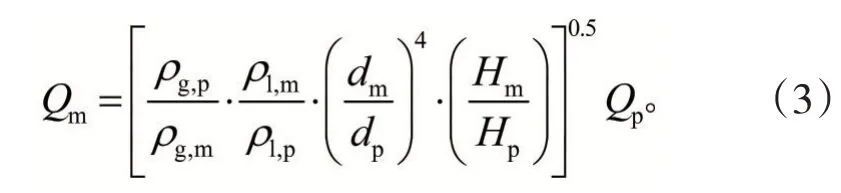
经过对气体密度的修正可得:

式中:Qm、QP分别为模型和原型供气流量,m3/h。
将修正参数代入上式可得模型与原型底吹气量的关系式为:

2.2 物理模拟试验方法
物理模拟试验采用“刺激-响应”原理。其方法为:在冶金容器注入流处输入一个刺激信号,信号一般使用示踪剂来实现,然后在容器出口处测量该信号的输出,即所谓响应,从响应曲线分析其流动状况及其对冶金反应的影响。
在冷态模拟试验中,通常使用电解质、发光或染色物质作为示踪剂。常用的示踪剂包括KCl 和高锰酸钾溶液,加入的方法有脉冲式加入或阶跃式加入。考虑到试验条件,本试验采用从钢包底吹气体上方区域脉冲加入KCl 示踪剂的方法。在钢包底部角部区域设置监测点,检测流体电导率随时间的变化趋势,当示踪剂浓度变化曲线波动值低于5%时则视为完全均混,如图1所示,记录tmix为均混时间[6]。

图1 钢包监测点示踪剂浓度随时间的变化曲线
2.3 物理模型的建立
按照相似比1∶3设计钢包物理模型,设计图如图2所示。采用有机玻璃制成的钢包模型,钢包支架由铝型材加工而成,为钢包模拟系统设计单独的供水管路。目前,钢包模型已经具备上述研究内容的试验条件。
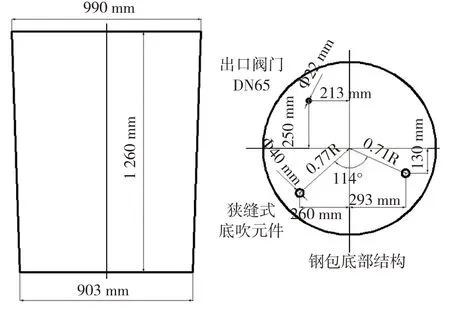
图2 钢包模型设计
2.4 钢包流体流动及均混行为试验研究
钢包底吹条件对于精炼过程具有重要影响,本试验重点研究单孔喷吹和双孔喷吹条件下钢包流体流动特征及均混行为。底吹元件布置位置和试验方案如图3和表2所示。以钢包出口所在的直径为对称轴,两侧分别在半径为226 mm和339 mm的圆周上布置底吹喷嘴。对于底部单喷,考虑到对称性,分别研究原 1#、12#、15#和 2#四个位置的底吹情况;对于双喷,分别研究原1#+2#、原1#+4#、12#+2#和12#+4#四种方案。底吹总气量分别为2 L/min、3 L/min和4 L/min。
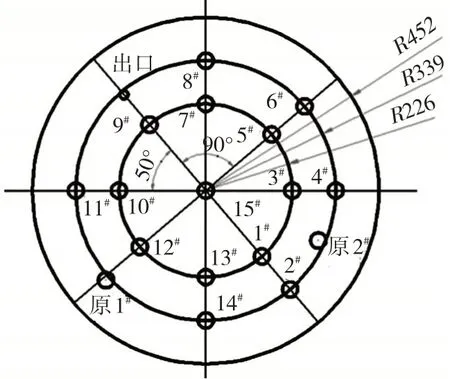
图3 钢包底吹元件布置位置

表2 钢包底吹实验方案
不同单喷条件下的电导率变化曲线如图4 所示,将浓度变化波动<5%时刻定义为均混时间。在单孔喷吹条件下,吹气位置逐渐向钢包底部中心靠近,均混时间逐渐缩短,并且当采用底部中心单孔喷吹时,均混时间最短,约为105 s。均混时间的变化与吹气钢包内的流场密切相关,在中心底部条件下,钢包内呈现对称的流动分布特征,最有利于电解质溶液的扩散。

图4 单喷条件下电解质溶液的电导率变化曲线
不同双喷组合条件下钢包内电解质溶液的电导率变化曲线如图5 所示。重点变换12#和原1#位置分别与2#和4#的组合方式,该组合方式的现场干涉最小。通过比较可以看出,将原1#位置向底部中心移动至12#位置处,并且选择与之呈135°分布的4#位置相组合,其对应的均混时间最短,约为75 s,比最佳的单喷15#位置均混时间还要短。此外,原1#与2#的组合方式对应的均匀时间仅次于最佳方案,其为120 s。所以,采用双喷的底吹方式更加有利于发挥钢包的精炼功能。
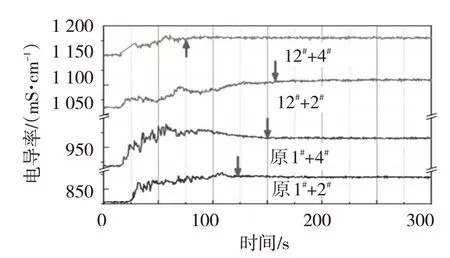
图5 双喷条件下电解质溶液的电导率变化曲线
图6和图7为原1#+2#和原1#+4#底吹条件下,不同吹气量所对应的均混时间曲线,对于原1#+4#组合,随着底吹气量的增加,均混时间逐渐缩短;而原1#+2#组合方式则在中间气量时达到最短均混时间。
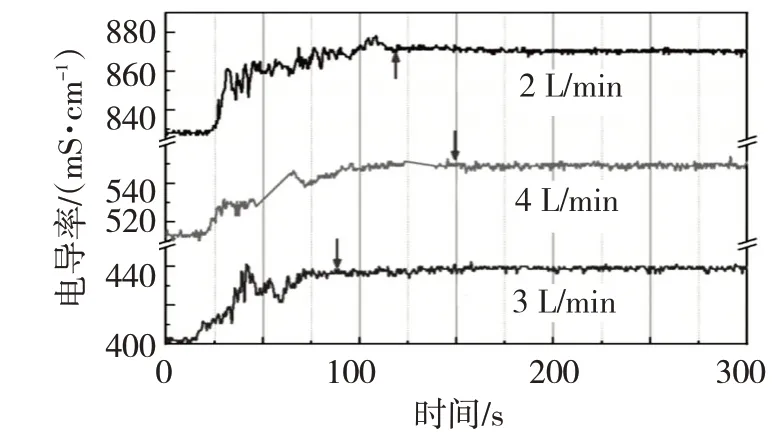
图6 不同底吹气量条件下电解质溶液的电导率变化曲线(原1#+2#)

图7 不同底吹气量条件下电解质溶液的电导率变化曲线(原1#+4#)
3 数值模拟试验研究
3.1 数学模型的建立
3.1.1 模型假设及控制方程
本数学模型主要基于如下假设:1)钢液和底吹气体均为不可压缩流体,整体流动为湍流流动。2)忽略流体温度梯度对流场的影响,假设整个流场温度均匀分布。3)忽略底吹气泡的破裂和聚合现象,假设气泡直径恒定。4)忽略顶渣对流体流动状态的影响,自由液面处理为气液两相交界面。5)假设反应器出口截面恒定,出口流量恒定。
钢包底吹氩过程数值模拟均采用欧拉两相流模型描述反应器内的气液两相流动行为。钢液和氩气视为相互贯穿的连续介质,对每一相均认为是三维稳定的湍流流动,分别建立各相的连续性方程、动量方程,采用标准k-ε 双方程模型求解有效黏度。气液相之间通过曳力、升力、虚拟质量力进行传递[7-10]。钢包内钢液和气相流动的方程如下。
1)连续性方程:
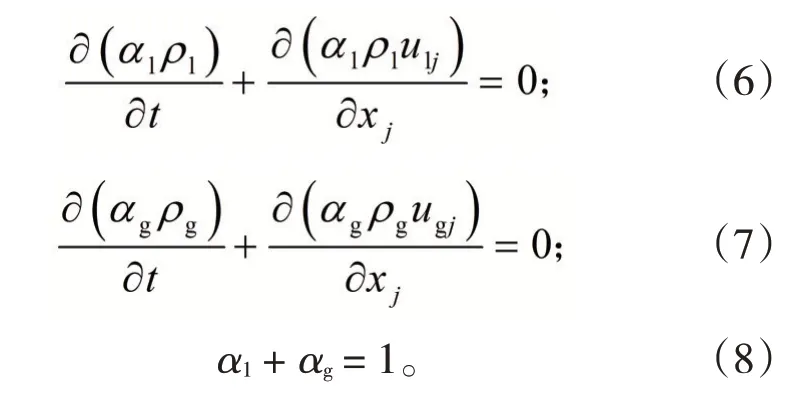
式中:下标l和g为液相和气相;α表示相体积分数;u为速度,m/s;ρ为相密度,kg/m3。
2)动量传输方程:

式中:i和j为 1,2,3 分别代表x,y,z三个坐标轴方向。Kg1和k1g为相间动量交换系数,定义为:
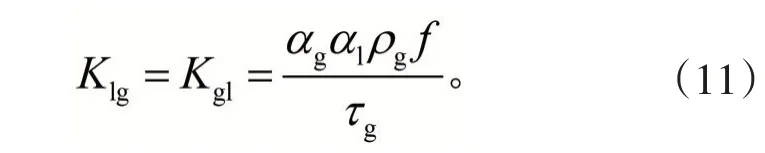
式中:f为曳力函数,对于不同的交换系数函数定义有所不同。τg为颗粒弛豫时间,定义为:
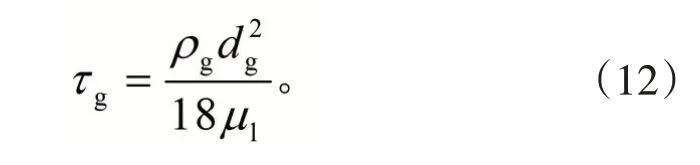
本计算中采用Schiller和Naumann曳力模型:

式中:CD为曳力系数。取值为:

其中Re为相对Reynolds准数,定义为:

式中:Flj和Fgj为气液两相间的非曳力(且Flj=-Fgj),包括升力Flift和虚拟质量力Fvm,即Flj=Flift+Fvm。其中,Flift=-0.5ρlαg(u1-ug)×(▽×ul)。
气相和液相的升力之间互为相互作用力,即:

气相和液相间的虚拟质量力为相互作用力,即:

湍流黏度μt定义为:
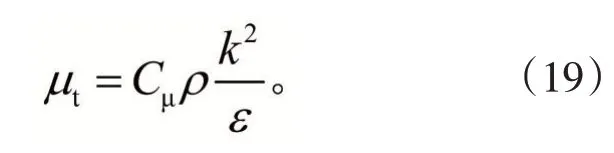
3)湍流传输方程。吹氩过程中,氩气的密度和体积分率要远小于钢液,因此本计算选用液相的kε湍流模型求解湍动能及其耗散率。
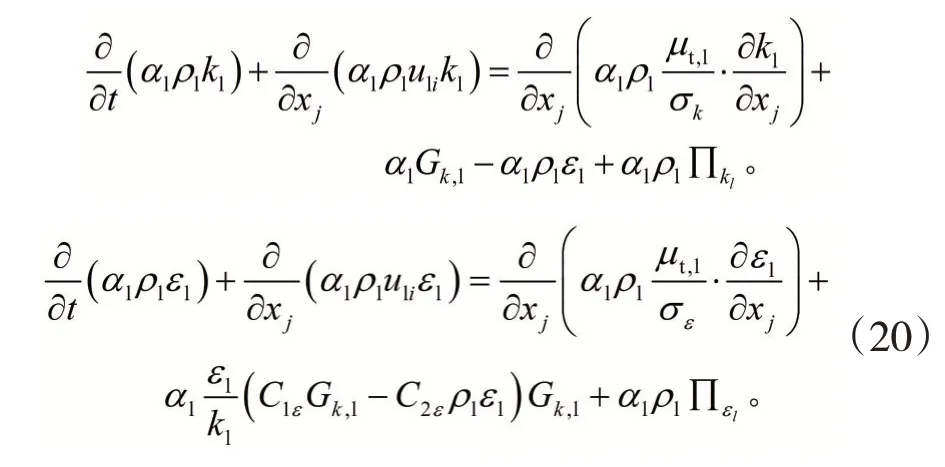
式中:Πkl和Πεl为气相对液相的作用;Gk,1为湍动能的源项,。
以上方程中的各经验常数采用Launder 和Spalding 的 推 荐 值 ,Cμ0.09,C1ε1.44,C2ε1.92,Ck1.00,Cε1.30。
3.1.2 模型的边界条件及初始条件
1)边界条件设置。a 氩气入口:钢包底吹氩气入口设为质量流量入口,氩气的质量流量按照体积流量换算。对于不可压缩流体而言,指定质量流量入口相当于速度入口,根据入口截面积就可将质量流量换算成入口速度。该边界流速和湍动能及耗散率的数学表达式如下:

式中:uz为根据质量流量换算得到的入口气体流速,m3/h;ρargon为氩气密度,kg/m3;A为吹气孔横截面积,m2;Kinlet为入口处的湍动能,m2/s2;εinlet 为入口处的湍动能耗散率,m2/s3;D为吹气孔直径,m;αg为气相体积分率。
b 自由液面:自由液面为Degassing 边界,该边界只允许气相逸出,不允许液相通过该边界。气相如何通过该边界取决于局部的气体压力,边界条件的数学表达式如下:

式中:ux,uy,uz为流体在x,y,z方向上的速度矢量;α为计算单元格内各相所占的体积分率;下标l 和g为液相和气相。
c钢包出口:稳定过程底吹气时,反应器内流体总量恒定,不存在出口边界问题。研究非稳态浇注时,随着浇铸过程的进行,自由液面不断下降,钢液的静压力逐渐减小,同时为了保证长水口钢液流量的稳定,需要逐渐增大滑动式水口的开口度,此时流经长水口钢液的流速也会降低。但本数值计算忽略了钢液静压力的变化对出口流速的影响,因此出口横断面尺寸设为恒定值,计算中出口钢液流量不变,该稳定流量根据对应连铸系统生产的铸坯断面尺寸和拉速确定。d 壁面:钢包壁面设为无滑移边界,即各变量在壁面处的值为零。近壁面附近采用标准壁面函数处理。
2)初始条件设置。钢包浇铸属于多相流非稳态流动过程,需要在迭代计算之初设置初始条件。本计算忽略钢包精炼后期吹气搅拌结束后钢包内流体的惯性流动,假设经过一定时间的静置之后钢包内流体流动速度为零;因此,本计算初始时刻钢包内流体整体速度为零。初始时刻由于尚没有气体吹入熔池,所以整个熔池充满了钢液相,只是在熔池上方存在一定厚度的气相层。
3.2 数值模拟结果分析
采用数值模拟方式研究了现场双喷条件下的流场,图8 为现用钢包的底吹位置及含气率模型,图9为含气率及密度分布云图。可以看出,不同含气率引起截面上的密度分布差异,依靠密度差产生浮力,进而驱动钢液流动。
图10和图11分别为两喷嘴截面上的速度分布和钢包内部整体的速度分布。可以看出,底吹喷嘴上方流体的流速最大,在喷嘴所在的纵向截面上形成了非对称的回环流动,正是该回环流促进了钢液在钢包内的均匀行为。从钢包顶部的速度分布看,两个喷嘴所形成的回环流动在其中间区域交汇,促使各自的流动转向,形成了大致垂直于两喷嘴连线方向的流动,该流股达到包壁后转为向下的流动,最终加速了钢液在钢包内部的流动和均匀行为。
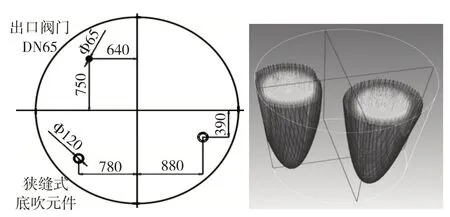
图8 现用钢包的底吹位置及含气率模型

图9 含气率及密度分布云图

图10 两底吹位置所在截面上的速度分布

图11 钢包内部及顶面的速度分布
4 结 论
4.1 不同含气率引起截面上的密度分布差异,依靠密度差产生浮力,进而驱动钢液流动。
4.2 单吹条件下,均混时间的变化与吹气钢包内的流场密切相关,采用双喷的底吹方式更加有利于发挥钢包的精炼功能。
