狭长型水库蓄水至初期运行阶段水温演化规律研究

刘有志，相建方，陈文夫，廖建新，程 恒，黄海龙

（1.中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室，北京 100038；2.中国三峡建设管理有限公司，北京 100038）

1 研究背景

超高拱坝是一种受温度和水压荷载影响较大的空间壳体结构，其中上游水库水温分布直接影响到大坝运行期稳定（准稳定）温度场的分布[1-2]。特别是对于坝体基础约束区，上游库底水温将直接影响到大坝的基础温差和温度控制设计标准的制定，而上游水库水温的分布及变化过程也会对拱坝全生命周期的运行工作性态产生影响，因而研究水库水温的时空分布和演化规律对拱坝安全意义重大。

苏联和美国在1930年代即开始重视水库水温的研究，前苏联在现场试验研究中做了大量细致的工作，美国在水温数学模型的建立和工程实践应用方面的研究一直在不断推进，其后的发展主要沿这两个方向进行。在数值方法的研究中，Raphael J M[3]、Orlob J T 等[4]、Huber W C 等[5]和Brooks N H等[6]的研究和应用推动了数值方法的发展，对于高坝水库分层的现象有了初步的认识；Edinger 等[7-8]开发了横向平均的LARM模型用于库水温和水质的计算，经过模型不断的改进和功能的完善，发展成了现在的能够应用于河流、湖泊、水库和海湾的二维横向平均水动力学和水质模型CE-QUAL-W2[9-10]，为解决计算过程中的数值耗散问题，该模型还多次进行了算法的改进[11]；与此同时，数值方法中还出现了三维计算方法，其中以集成了水动力学模块、泥沙输运模块、污染物运移模块和水质预测模块等多个模块的EFDC为代表[12]。中国1980年代开始大规模兴建混凝土坝时，主要通过类比同类工程的水库水温实测资料，来拟合得到了水库水温的预测经验公式，如中国混凝土拱坝设计规范[13]中推荐的水库水温计算公式，就是朱伯芳提出的经验公式[14]。但实践表明，该方法主要适用于100 m 级的水库大坝，且无法考虑大坝成库过程中水温变化过程的模拟对于垂向分层明显的水库，胡平等[15]结合工程实际开发了一维垂向计算方法，在一些水库的计算和预测中达到了较好的效果，但大坝成库过程中水温变化过程的模拟过程仍无法实现。近年来，随着200 m 级以上高库大坝建设的逐渐增多，经验公式法已难以适用于高坝水库水温的模拟，数值模拟方法得到越来越多专业人员的关注和研究，如蒋红[16]、邓云[17]、张俊华等[18]、章若茵等[19]对溪洛渡等大型水库的水温或流沙异重流模拟预测方法进行了研究，这些算法以水库建设前的预测或者室内实验为主，未及进行正式蓄水后的跟踪研究，对于这些算法和理论缺乏系统的验证和反馈。

现有的文献资料表明，坝高200 m 以上的水库还未进行过从开始蓄水到运行初期库水温温度演化规律的专门研究。以溪洛渡水库为例，当水库水深较深、库容较大时，原来的研究成果不能直接用于这类水库，需要将模型和实际的蓄水过程、气象条件及水文条件等多种影响因素相结合来分析。因此，狭长型高库大坝的水库水温模拟问题在实践中依然非常复杂，如何有效模拟此类水库的真实水库水温分布及变化规律仍是业内关注的重点难题。

2 水库水温计算的3种方法简述

当前大型水库水温计算方面的研究较多，但是并没有根据河道的形状对水库类型进行细分。笔者通过多座水库的对比研究发现，二维算法更加适用于河道狭长，且水库宽高比小于1的水库，该类水库往往水深较深，一维算法适用于水库上游表面开阔的水库，坝体多为重力坝结构，而经验公式方法具有广泛适用性，但是缺点是精度不够，无法满足精确模拟的要求，且无法考虑大坝成库过程中水温的变化过程。对于本文研究的水深较深的狭长型河道上的水库而言，CE-QUAL-W2 在模拟水库水动力学过程和密度梯度作用方面有着先天的优势。

2.1 CE-QUAL-W2CE-QUAL-W2是一个考虑纵向和垂向的二维水动力学与水质模型。由于该模型假设横向平均，因而最适宜模拟像本文这样的狭长河道型水库的纵向和垂向的水质梯度。该模型之前已经被用于河流、湖泊、水库等水体的计算中。该模型能够计算水体自由表面、垂向和纵向的流速，以及温度。本文选用ULTIMATE 算法求解水动力输运方程，该算法能够减少不真实的物理过程，更加符合本文的计算。同时，在求解过程中，CE-QUAL-W2 还提供了一个可控制垂直对流解法时间权重的参数THETA，当取0时是完全的显式格式，当取1时是完全的隐式格式，当取0.5时对应的是Crank-Nicholson 解法，本文按照建议选取THETA为0.55。该模型还提供了多种湍流模型，经过对比验证，本文选用k-ε模型。

由于按照静水假设进行计算，垂向的动量方程没有被考虑在内，该模型可能会在有明显垂向加速度的情况下得到不准确的结果，比如在初期的快速蓄水阶段等过程中，因而仍需要在实际模拟中校正。关于CE-QUAL-W2的理论研究部分，在说明书上已经有详细的介绍[9-10]，在此不进行赘述，在此仅列出主要控制方程。

X方向动量方程（X-momentum）：

Z方向动量方程（Z-momentum）：

连续性方程（continuity）：

状态方程：

自由表面方程：

式中：U为水平速度，m/s；τx为x方向上的平均剪切应力；W为垂直速度，m/s；τz为z方向上的平均剪切应力；B为通道宽度；ρ为密度；q为压力；η为水面高程；为考虑温度、总溶解固体或盐度、无机悬浮物的密度函数。

2.2 一维算法关于将一维算法作为对照算法，在此做简要描述。可取出一个微元，研究其热量运动，计算模型简图见图1。

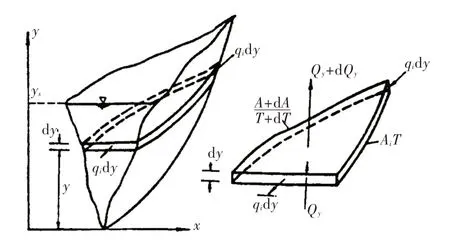
图1 一维水库水温计算模型简图

（1）垂直向：单位时间内由下面进入的流量为Qy，带进的热量为cρQyT ；单位时间内由上面流出的流量为Qy+dQy，带走的热量为：

故单位时间内净带进热量为：

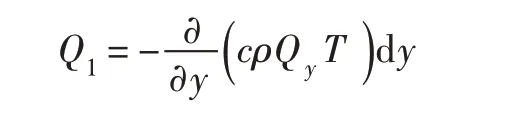
（2）水平向：单位时间内入库带进热量为cρiqiTidy；出库带走热量为cρq0Tdy ；故单位时间内净剩热量为：

（3）由短波辐射热：

自下边离去的辐射热：

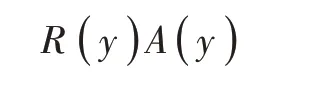
自上面进入的辐射热：

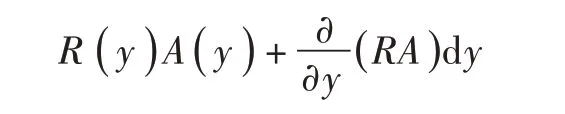
留下的净辐射热为：

（4）由扩散作用：

下边进入：

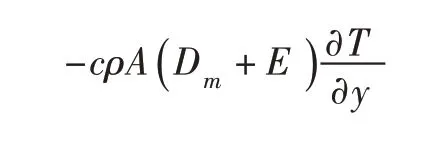
上边流出：

净流入为：

（5）水体升温吸热：

式中：c为水的比热；ρ为水的密度；T为水的温度；qi为入库水流单位高度的流量；Ti为入库水流的温度；q0为出库水流单位高度流量；ρi为入库水流的密度；R（y）为高度y 处的短波辐射热；k为辐射热的衰减系数；A（y）为y 处的水库面积；Dm为水分子扩散系数；E为水的紊动扩散系数。由热量平衡可知：

则有：

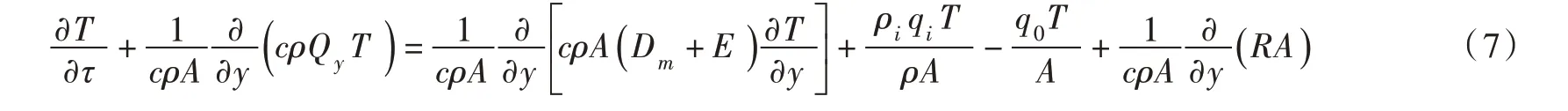
2.3 经验公式算法朱伯芳院士方法是经验公式法的代表，在中国混凝土拱坝设计中被广泛采用，本文对其进行简要介绍[13]。

库水温度T（y，τ）是水深y和时间t的函数，可按下列方法计算：

任意深度的水温变化

任意深度的年平均水温

水温相位差

式中：y为水深，m；τ为时间，月；ω为温度变化的圆频率，ω=2π/P；P为温度变化的周期，12个月；ε为水深y 处的水温滞后，即对于气温的相位差，月；T（y，τ）为水深y 处在时间为τ时的温度，℃；Tm（y）为水深y 处的年平均水温，℃；Ts为表面年平均水温，℃；A（y）为水深y 处的温度年变幅，℃；τ0为气温最高的时间，月；d、f、γ为经验拟合系数，分别取为2.15、1.30、0.085。

3 大型水库水温现场反馈与分析

3.1 模型的建立溪洛渡水电站工程属于中国西南地区金沙江梯级开发中的第三梯级，最大坝高285.5 m，坝顶高程610 m，水库正常蓄水位600 m，死水位540 m，汛期限制水位560 m，距上游白鹤滩水电站约200 km。大坝2013年初开始下闸蓄水，2013年6月水位蓄水至540 m，2014年10月首次蓄水至600 m，2015年6月水位回落至540 m，2015年10月水位再次到达600 m。

库区河谷较窄，河道宽度在600 m 左右，且河道较深，为典型的U 形河道，库区地形图如图2所示。根据实际河道地形信息进行网格的划分，纵向分为56 段，每段长度4 km，垂向分为72层，每层深度4 m，由于计算范围较大，网格数目较多，为减少计算量，本文采用的计算网格是满足网格对计算结果无影响条件下的最大尺寸·网格，纵向、垂向和俯视网格如图3所示，其中图3（b）为近坝段垂向截面网格。

3.2 初始边界与参数选择本次模拟计算的输入文件中，河道地形信息采用溪洛渡地区的实际测深数据，气象资料采用近坝区气象站的实测气温、露点温度、云量、风速和风向，太阳辐射对库水温度的影响按照当地实际经纬度位置、实际云量和山体高程等遮蔽信息计算。来水流量采用主河道水文站测得流量，出水流量按照电站实际的调度过程给出，该水库以发电为主要目的，出水口的位置仅考虑电站引水口，由于以上输入信息均按照实际给出，因而计算过程中的水位与实际水库的水位过程一致。

溪洛渡库区底部堆渣区实测资料显示，库区底部水温在15℃左右，库底以下10 m 处的岩石温度在21℃左右，温度高于一般地质条件下的温度，水和岩石接触面的温差为6℃，两者之间存在一定热交换，库底的热交换必须考虑在内，热交换系数Kw应取为比通常情况下的参数稍大[8-9]，可取为0.4 W·m-2·℃-1。

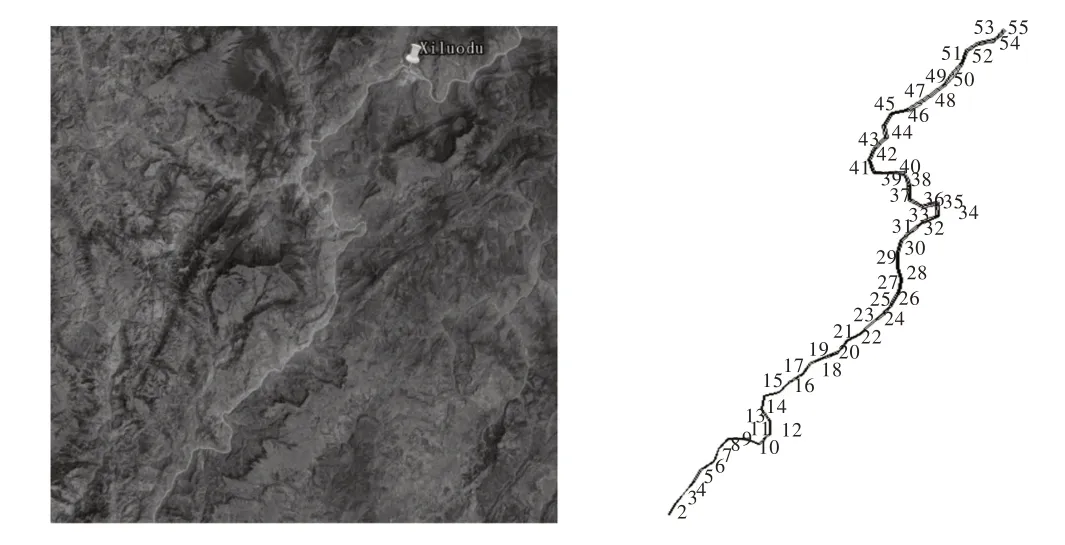
图2 库区地形图

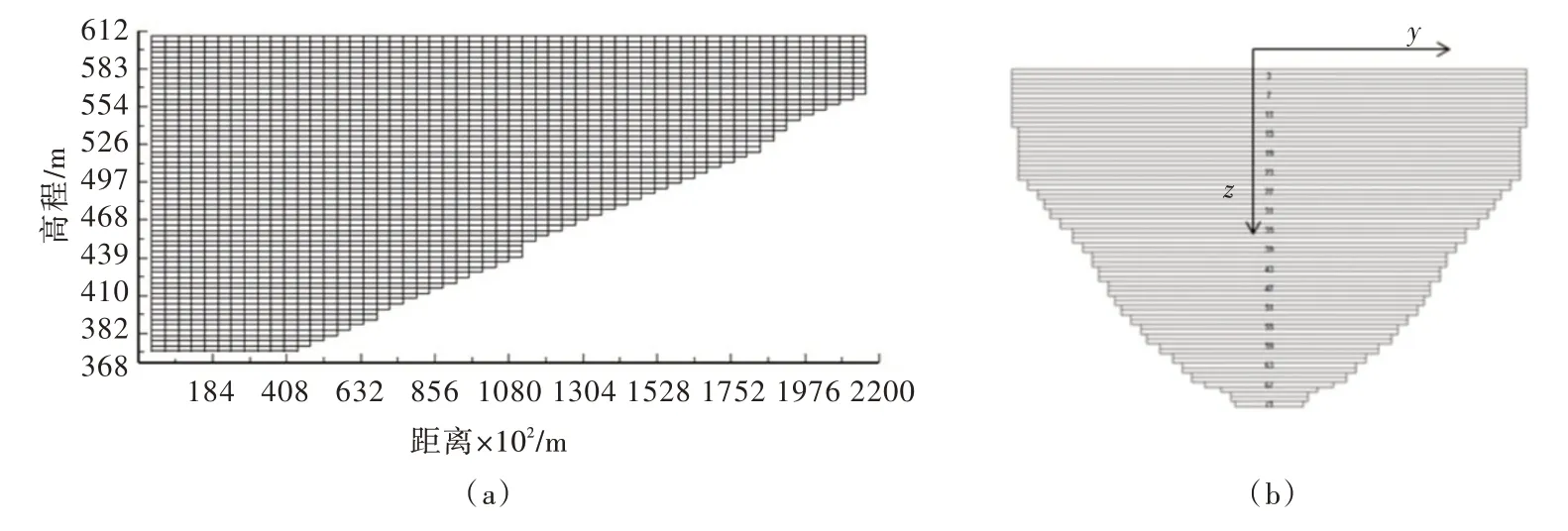
图3 纵向和垂向网格

3.3 现场监测数据对于溪洛渡这样的不完全年调节水库而言，来流流量、出流流量、来流温度和气温、辐射等气象条件是影响水温分布的直接因素，其中来流流量、来流温度是影响库水温的主要因素。为满足计算的需要，也为保障数值模拟计算精度，本次反馈分析同时考虑了干流和支流上的水温和流量资料，在原水文站中增设温度计测量来水温度，同时增设了两个临时测站来测量支流的流量和温度情况，这些测站均于2012年布置完成并能够取得测值。此外，气象条件由于影响作用范围有限，直接采用坝址区测站的数值。

获取水库水温的实测值是本次研究的重要内容，为获得准确的坝前水温值，在大坝的31个坝段中选取6#坝段、10#坝段、16#坝段、22#坝段和27#坝段共5个典型坝段来实地测量其坝面上游的水温，可正常使用的温度计共108 支，测点最低高程373 m，最高高程604 m 高程，具体布置位置如图4所示。温度计采用高精度电阻测温计，测得水温精度能够达到0.01℃。从2012年3月1日开始取得测量初值，每12 h 取一次读数。

温度换算公式：

式中：R0为0℃时的电阻，电阻值为46.60 Ω；Rt为任意时刻实测温度下阻值；K为温度系数，单位为℃/Ω。

图4 坝前温度计布置位置示意

图5 多年平均水温与坝前实测水温对比图

图6 工程设计出、入库流量与实际出、入库流量对比

与工程可行性研究阶段的多年统计数据相比，进、出库流量，来水水温等资料均出现明显的变化。图5—6是初步设计阶段和现阶段来水温度、水库进、出流量等关键因素的对比，可以看出，大坝实际蓄水时上游来水水温在某些月份明显高于多年平均统计河水水温，实际流量与设计流量过程也有较大差别。

3.4 计算结果对比分析图7所示的坝前水温温度计的实测值和计算值变化过程线对比可知，采用实际监测资料对库区水温模拟的计算结果基本上能够反应出实际水温变化的趋势，多数情况下与实测值吻合较好（大坝坝前堆渣至370 m 高程，2012年3月15日基坑开始进水，2012年7月到400 m 高程，2013年1月水位450 m 高程，2013年6月水位540 m 高程，2014年10月蓄水至600 m 高程）。相对而言，在蓄水的前期水位较低、来水湍流现象突出、不同来水水温混掺过程较为剧烈时，模拟结果与实测值的误差值相对较大。2013年水位升高之后的计算基本上能够反映真实情况，平均误差不超过1℃。每年的平均误差可按照下式来计算：

得到下表：

表1 蓄水后3年平均误差 （单位：℃）

从表1可知，2013—2015年平均误差逐年减小，可以推断随着水位蓄至正常水位后，水流的波动剧烈程度减小，同时各种因素的可控制性增加，计算方法中对于二维计算的基本假设和相应的湍流模型更加接近真实状态。

由上述分析可知，所建的河道模型能够反映溪洛渡库区水温的变化规律，模型的适用性和可信度较高，随着水位的相对稳定和计算时间的增加，计算的平均误差会进一步减小。

4 结果与讨论

基于上文的计算分析成果，可对该类型水库从蓄水到初期运行阶段的水温演化规律做进一步的分析研究。

图7 典型高程温度过程线

（1）3种数值方法的差异。如下图8中所示，由2015年10月19日实测值与3种计算方法计算结果的对比可知，经验公式获得的水温分布情况与实际值差异较大，表明对于高拱坝而言采用该公式是不合适的；设计阶段采用基于多年平均统计来水水温、流量等参数的一维算法获取的水温分布规律与实际水温分布规律类似，但数值误差较大；本文采用边界条件精确处理后的CE-QUAL-W2模型，并且考虑了蓄水过程，所获得的水温分布与变化规律与实际情况吻合更好。图中实测值是2015年10月19日，水位600 m时的实测值，方法1为朱伯芳经验公式法，方法2为设计阶段一维算法，方法3为本文采用的CE-QUAL-W2模型算法。

（2）水温垂向分布情况对比分析。本文关于水库水温的跟踪模拟计算从2012年3月围堰拆除开始到2015年10月截止，历时3年8个月。各个典型时刻沿高程方向水温分布情况如图9所示，图9（a）为2013年6月20日首次蓄水至540 m 高程，由于在该阶段的蓄水过程中，50 d 内水位上升了100 m，库容增加了53 亿m3，该过程水体充分掺混，因而未出现明显的分层现象；图9（b）为蓄水进行了18个月后，第一次蓄水至最高水位600 m 高程，水温的垂向分布已经出现了明显的分层，与以往认为水库水温分层需要很多年的认知有所不同，同时由图可知，刚蓄水至最高水位时，计算与实际的温度值基本吻合，但分层位置仍稍有差异，随着成库后水体的进一步稳定，这种差异逐渐减小，如图9（c）（d）所示，可见数值模拟的过程与实际的物理过程能够基本吻合。其中，图9（a）（d）中470～530 m 高程之间实测值波动较大的原因是受到汛期孔口泄流的影响。

图8 实测值与3种方法对比

图9 典型时刻不同坝段上游温度测量值与计算值对比

（3）蓄水初期前3年水库水温变化规律。由计算结果可知，溪洛渡水库水温基本在蓄至正常水位后第二年3月份开始出现分层，随后水温的空间分布随流量和温度等因素的变化而变化，蓄水初期水库水温变化情况见图10。由图可知，水体的温度变化基本上可以分为8个典型区域：在接近水面区域，由于受来水、气温和太阳辐射的影响，温度随时间变化波动较大，温度年变幅约13℃，典型温度过程线如图11中536 m 高程过程线所示；在接近水面区域以下，水库中存在大面积的温度过渡区，在上下层温度传导过程中起到过渡的作用，对比图11中4 条过程线可以明显看出温度层层传递并逐渐减弱的过程，从水库水位上升至560 m 高程后的次年春季开始，536 m 高程温度的极大值出现在7、8月份，475和431 m 高程温度的极大值出现时间逐渐后移，并且量值减小，374 m 高程的温度过程线几乎为水平，过渡区域温度年变幅基本在3.2～10.2℃左右，高程越低变幅越小；从2015年以后，库底水温基本处于相对稳定状态，年变幅小于1℃，该区域温度基本稳定在某个温度值附近，上部边界的影响很难传播到该区域，典型情况如图11中374 m 高程过程线所示。

（4）水库水温长期运行规律。为了解溪洛渡多年运行后水库水温可能的变化趋势，模拟从最初蓄水一直计算至2040年12月的计算工况，其中，2016—2020年的输入数据分布采用2013年和2014年的数据（即来水水温一年低，一年高，其他参数保持不变），2021—2040年后，均采用2014年10月—2015年10月的实测数据，得到如下图12所示的结果。

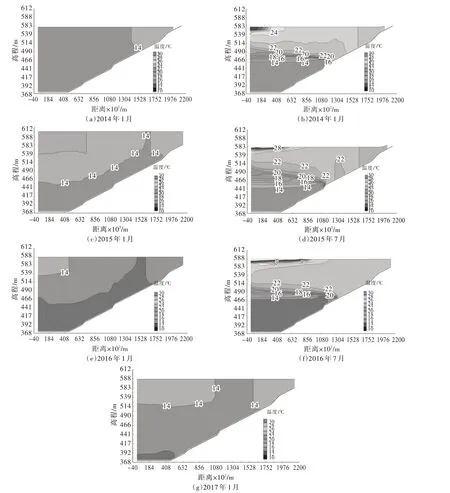
图10 蓄水后水库水温变化云图

图11 16#坝段不同高程上游表面温度计温度变化过程线

溪洛渡的水体特点是水深较深，同时库容较大，这在一定程度上有利于水体的稳定，尤其对于下层而言，除与岩基发生热交换之外基本不受外部影响。底部水体在趋稳的同时，由于受上层和基础传导的热量的影响，当上游来水温度稍高时，温度会略有回升，而当1月份上游来水温度低于底部温度时，1月份的低温水会直接沉入底部，使底部温度重新回到较低的状态，即底部库水温度将随着上游来水温度的变化轻微波动，但总体处于相对稳定状态，而上部水体温度则将如图12所示呈现出不同程度的波动。

从多年的预测结果可以看出，溪洛渡水体会在短期内出现分层并有一个相对稳定的状态，但是极易受年际上游来水水温变化的影响，没有绝对的稳定状态，尤其是上部浅层区域。

由上述分析可以推测，接下来的运行阶段，若不遇到极端年份，各高程的水温将会随时间每年呈近似周期性变化，并且随着深度的增加年变幅减小。上部520～600 m 高程范围内，随季节和水位的改变，温度变化较为明显，变动范围在15～27℃之间，年变幅为12℃；450～520 m 高程的70 m 范围内，水体传热作用层层减弱；450 m 高程至库底的范围内基本上常年稳定在15℃左右，接近冬季最低河水温度。

图12 374m、450m和520m 高程温度长期预测过程线

5 结论

本文主要取得以下几个方面的结论：（1）本文在高坝大库中引入二维横向平均的水动力模型CE-QUAL-W2，按照真实的边界条件对该水库从开始蓄水到初期运行历时近4年的温度变化过程进行了模拟分析，得到的计算结果与实测数据吻合较好，验证了该模型对于溪洛渡水库的适用性。（2）从蓄水到初期运行的整个过程中，当水位较浅时，水体的水温变化规律依然表现为天然河流的特性，当水位逐渐增加至水库正常蓄水位的过程中，水体的温度开始逐渐表现为水库的特性。研究发现，成库后约半年时间后，溪洛渡水库能形成4个典型的区域，每个区域的温度年变幅不同，其中过渡区区域最大，年内不同特征位置的水温极大值出现时间逐渐后移并减小，原来出现在高温季节的水温极大值后移至年末，至接近水库底部时年变幅几乎为零；此外，水库长期运行的预测研究表明，库底温度除受上部水体的微弱影响之外，还主要受冬季低温水体的影响，如果遇到极端年份，则有可能会打破库底水温原有的平衡。（3）中国还有一批类似溪洛渡拱坝的其他300 m 级的特高拱坝在建、拟建或规划建设，如白鹤滩、乌东德及松塔等电站。本文多年水库水温跟踪仿真分析的成果及水温变化分布规律研究可以为这些电站的大坝温控防裂及结构设计提供有益的借鉴。