基于敏感性分析与粒子群算法的拱坝原型动弹性模量反演方法

李火坤，王 刚，魏博文，黄 伟，陈良捷

（南昌大学 建筑工程学院，江西 南昌 330031）

1 研究背景

我国的高拱坝多位于西南高山峡谷地区，随着一批新建高拱坝相继投入运行，复杂的地质条件及自然环境给长期服役的高拱坝带来不同程度安全隐患[1-2]。高拱坝的物理力学参数对精准评估大坝结构整体运行性态至关重要，目前获取大坝物理力学参数的主要方法有现场取样测试法和基于监测资料的反演法[3-4]。现场取样测试法工作量大，损坏原结构，且只能了解大坝局部结构参数特性，不经济也不全面。而原型监测资料蕴含了大坝真实的工作性态，因此利用大坝监测资料反演大坝及地基物理力学参数是一种有效的方法。

利用监测资料进行大坝物理力学参数反演的方法主要分为基于静态监测资料的反演方法和基于振动测试的参数反演方法两种。其中，基于静态监测资料（如静力位移）的大坝物理力学参数反演在近几十年来一直是大坝安全监控研究领域的热点，并取得了丰硕的研究成果[5-10]，为保障我国大坝的安全运行做出了重要贡献。近年来，随着结构动力参数辨识技术的发展，基于振动测试的结构物理力学参数反演研究发展迅速[11]，由于振动实测响应所包含的振动模态信息更全面地反映了结构整体力学行为特征，因此根据振动模态参数进行大坝物理力学参数反演所得到的结果更符合实际。冯新等[12]探讨了一种基于不完全模态观测数据的混凝土坝分区弹性模量反演方法，建立了基于不完全模态数据的大坝弹性模量优化反演模型；康飞等[13]基于不完全模态测试数据提出了一种混合单纯形人工蜂群算法进行动力材料参数识别方法；程琳等[14-15]根据大坝强震监测数据识别了某混凝土坝的振动模态参数，并建立了反映大坝动弹性模量和各阶模态参数之间非线性关系的多输出支持向量机代理模型（M-SVM），结合遗传算法对大坝弹性模量进行了反演；王登刚等[16]考虑模态观测数据的不确定性，引入不确定问题求解的区间分析思想，建立了利用先验约束条件的混凝土重力坝动态参数的区间反演模型，采用约束变尺度法求解获得了坝体混凝土和基岩动弹性模量参数的区间范围。文献[17]提出了基于遗传算法的拱坝材料参数反演方法，但结果验证中仍存在少部分测点精度不高等问题，仍需进一步改进。

本文以二滩拱坝为研究对象，提出一种基于敏感性分析与粒子群算法的拱坝原型动弹性模量反演方法，建立反映拱坝及地基各分区动弹性模量与拱坝模态参数非线性映射关系的三阶多项式响应面数学模型，基于正交试验法分析拱坝及地基的动弹性模量区域对拱坝模态参数的敏感性，确定待反演的动弹性模量区域；基于拱坝原型振动模态参数，提出基于响应面数学模型计算模态参数和原型振动模态参数的拱坝及地基分区动弹性模量反演最优化数学模型，建立参数反演的目标函数并采用自适应惯性权重的粒子群优化（AWPSO）算法进行寻优求解，最终反演出拱坝及地基各分区实际动弹性模量。

2 拱坝及地基分区动弹性模量反演方法

2.1 响应面数学模型响应面法是以数学理论和统计方法为基础，通过近似构造一个具有显式的函数表达式来拟合变量之间的非线性数学关系。本文采用响应面法来表述拱坝及地基分区动弹性模量与拱坝模态参数之间的非线性映射关系，以拱坝固有频率和振型作为模态参数变量，在准确表达拱坝动弹性模量和模态参数之间的非线性函数关系并充分考虑计算效率的前提下，采用三阶多项式响应面方程来表达动弹性模量E与频率f、振型φ之间的关系，建立的响应面模型如下：

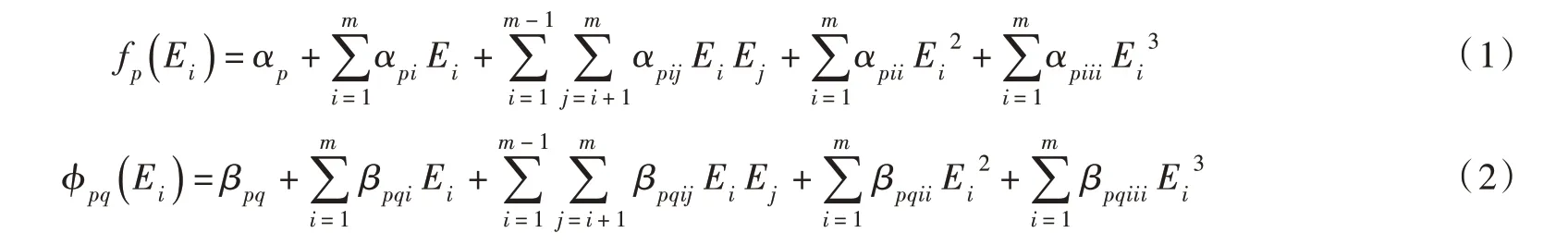
本文采用拉丁超立方抽样法生成动弹性模量样本，通过建立拱坝三维有限元模型并计算不同动弹性模量样本组合下的拱坝模态参数，根据式（1）和式（2），采用多元回归方法拟合动弹性模量与频率、振型之间的响应面模型，并以此替代有限元模型。

为确保拉丁超立方抽样法抽取的动弹性模量样本均匀覆盖取样区间，在动弹性模量的取值范围内均匀生成U个动弹性模量样本点时，将归一至并分成U 等份（即抽样区间为在每个抽样区间内以不等且随机的抽样概率生成样本，如图1所示。

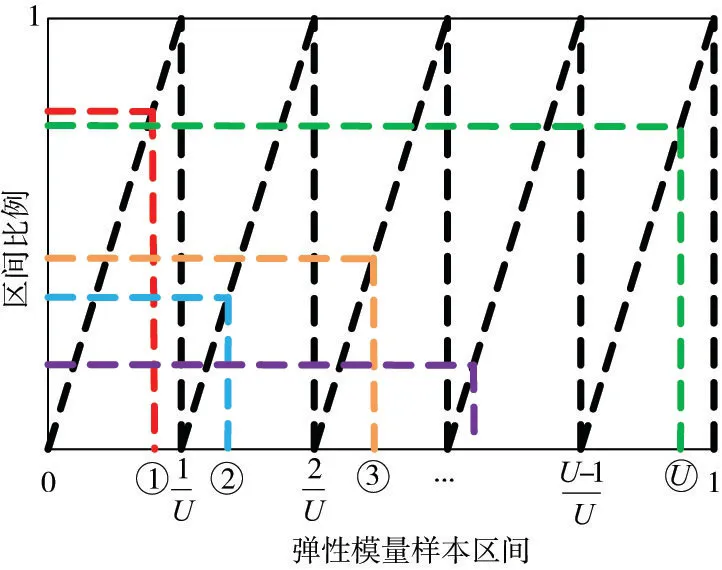
图1 拉丁超立方抽样方法

在拟合响应面方程时，响应面的精度是评价响应面模型是否合理的重要指标，本文以有限元模型模态参数（即固有频率fp和节点归一化振型φpq）计算值与响应面模型模态参数输出值之间的相对误差来衡量响应面数学模型的精度，其表达式如下：

式中： Re为响应面模型的精度，本文响应面模型精度控制5‰以内；yRS为响应面模型模态参数的输出值；yFEM为有限元模型模态参数的计算值。

2.2 敏感性分析式（1）和式（2）中动弹性模量的个数m 直接影响到动弹性模量反演的计算效率和精度，为合理选取对拱坝模态参数敏感性高的待反演动弹性模量区域，本文采用正交试验法[18]分析不同动弹性模量区域对拱坝模态参数的敏感性，以拱坝第一阶固有频率作为评价指标评价各动弹性模量区域对拱坝模态参数的敏感性，采用方差分析法对评价指标进行分析。

首先，计算所有动弹性模量区域组合下拱坝第一阶固有频率总离差的平方和Sr、各动弹性模量区域对拱坝第一阶固有频率离差的平方和SA及试验相对误差离差的平方和SE，其表达式如下：

其次，计算试验总自由度ZT=K-1、各动弹性模量区域数自由度ZA=u-1，并确定试验相对误差自由度以此计算第A个动弹性模量区域的方差试验相对误差的方差

最后，构造动弹性模量第A个区域对拱坝第一阶固有频率敏感性的统计量TA：

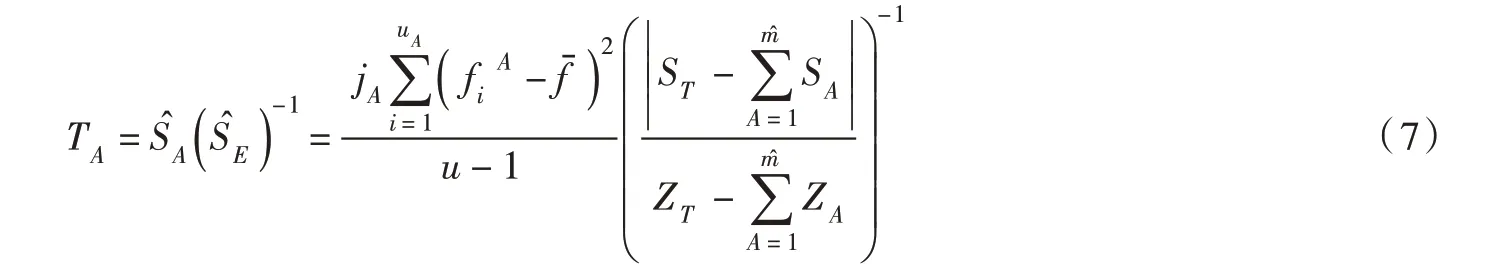
由上述过程可判别拱坝及地基不同动弹性模量区域对拱坝模态参数的敏感性。根据文献[19]关于方差显著性分析的研究成果，本文选取显著性水平λ分别为0.025、0.05、0.1 来确定不同动弹性模量区域对拱坝第一阶固有频率的影响并将其划分为4个等级，即：（1）视为影响高度显著；（2）视为影响显著；（3）视为有一定影响；（4）视为无影响。由此，可确定拱坝及地基待反演的动弹性模量区域。

2.3 最优化目标函数以拱坝原型振动模态参数与响应面数学模型计算模态参数的相对偏差作为目标函数J，将拱坝固有频率和各测试节点归一化振型的响应面数学模型计算值与拱坝原型识别值相比较，从而将拱坝及地基分区动弹性模量的反演问题转换为目标函数的最优化求解问题，构造的目标函数如下：

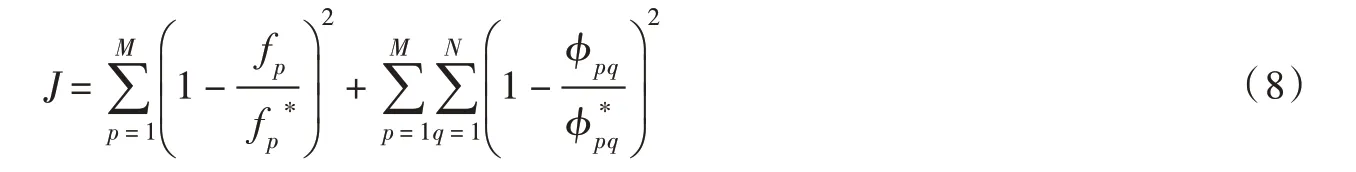
本文采用基于经验模态分解法（EMD）和奇异熵定阶的随机子空间法开展原型拱坝振动模态参数识别，具体过程可参考文献[20-21]。

2.4 自适应惯性权重的粒子群算法采用粒子群优化（PSO）算法对目标函数J进行最优化求解。为实现最优解的收敛和避免陷入局部最优，利用自适应惯性权重对PSO 算法进行优化，使其在搜索过程中能够依据粒子的位置动态变化，从而搜寻到最优解，其基本过程如下。

假定待反演的动弹性模量区域个数为m，由n个粒子组成一个初始群落，则在n×m 空间中，其初始粒子群E为：

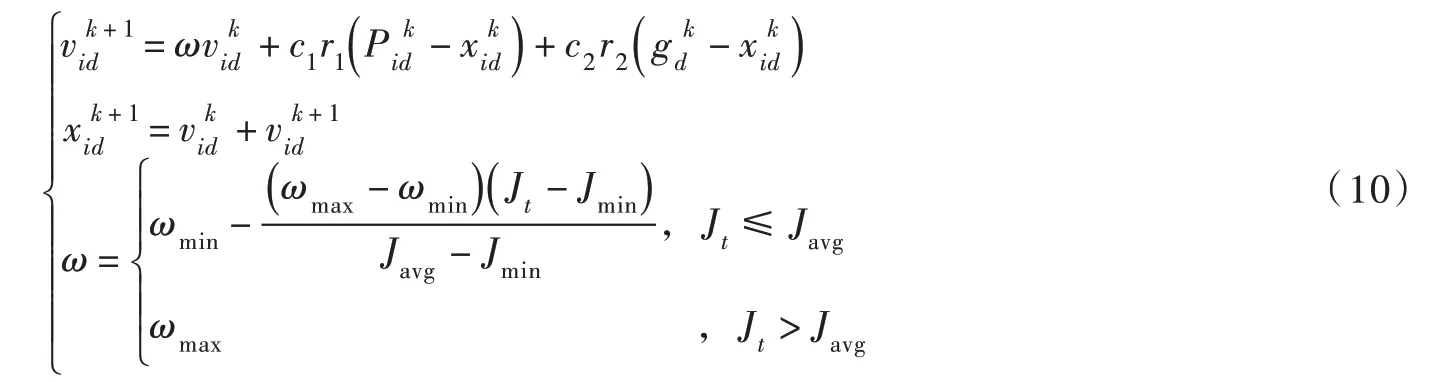
式中： c1、 c2为学习因子；r1、 r2为[0，1]范围内的均匀随机数；分别为粒子i 第k 次迭代中第d 维的速度与位置；为粒子i 第d 维的个体适应值最小处位置；为粒子群体第d 维的种群适应值最小处位置；ω为惯性权重；ωmin、 ωmax分别为惯性权重的最小值和最大值Jt表示粒子实时的适应值；Javg、 Jmin分别为当前所有粒子适应值函数的平均值和最小值。

当达到迭代次数或者停止条件时，则停止搜索并输出最优值，否则将继续迭代并更新粒子，直至搜索到满足收敛准则的值为止。

2.5 反演流程拱坝及地基分区动弹性模量反演流程如图2所示。基本步骤说明如下：（1）步骤1。基于EMD对拱坝原型振动响应信号进行降噪处理，计算降噪后信号奇异熵增量并确定拱坝振动模态阶次，采用随机子空间法识别拱坝原型振动模态参数；（2）步骤2。根据拱坝及地基弹性模量分区设计情况，建立拱坝流-固耦合三维有限元模型，计算拱坝及地基不同动弹性模量分区情况下的拱坝模态参数；采用正交试验法确定拱坝模态参数敏感性高的待反演动弹性模量区域；（3）步骤3。采用拉丁超立方抽样法生成动弹性模量样本集，以此作为有限元模型参数输入，计算各样本集下所对应的拱坝模态参数（频率和振型）；（4）步骤4。构建反映拱坝模态参数与各分区动弹性模量之间非线性映射关系的响应面数学模型，以步骤3的计算结果为依据，采用多元回归法确定响应面数学模型；（5）步骤5。基于拱坝原型振动模态参数与响应面数学模型计算模态参数的相对偏差最小，构建拱坝及地基分区动弹性模量反演的目标函数；利用AWPSO 算法进行优化求解，最终反演出拱坝及地基实际动弹性模量。

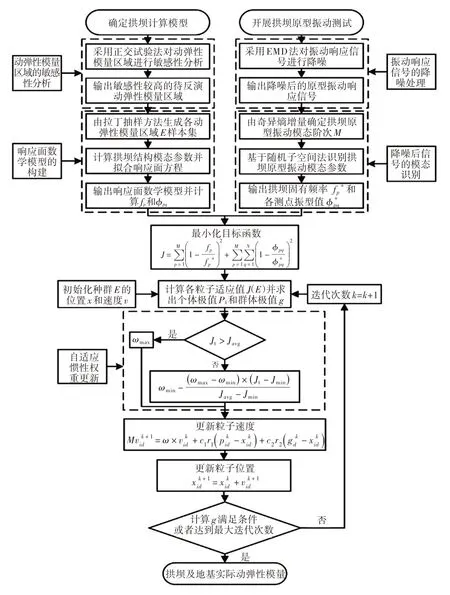
图2 拱坝及地基分区动弹性模量反演流程

3 二滩拱坝原型工程实例

3.1 原型振动响应测试情况本文以二滩拱坝为研究对象，开展了泄流激励下的拱坝原型振动测试，将径向动位移传感器布置于坝顶及拱冠梁处；其中，坝顶共布置7个测点，编号为B1 至B7，如图3所示；拱冠梁共布置4个测点，编号为B8 至B11，如图4所示。传感器为DP 型低频动位移传感器，其参数见文献[11]。测试工况如表1所示，采样频率为200 Hz，拱坝典型测点（B5）原型振动响应时程线如图5所示。

表1 原型振动测试工况

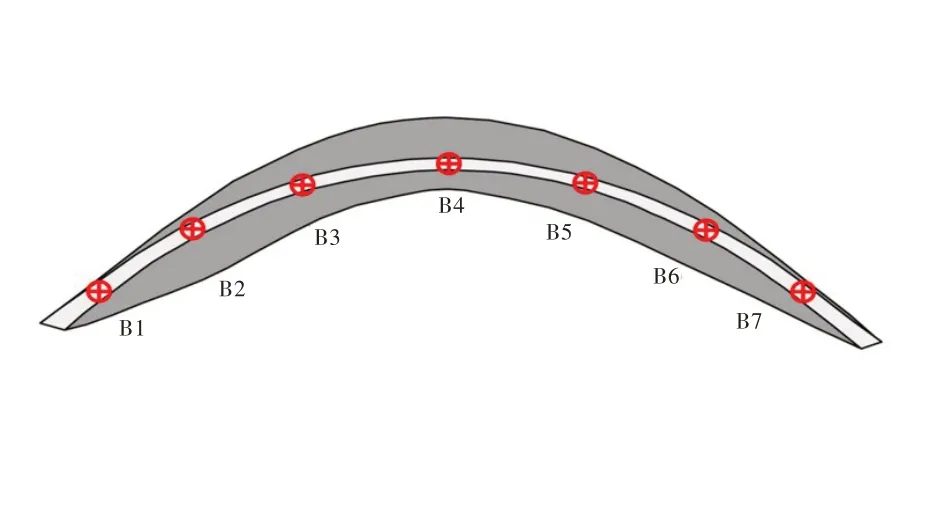
图3 坝顶测点布置

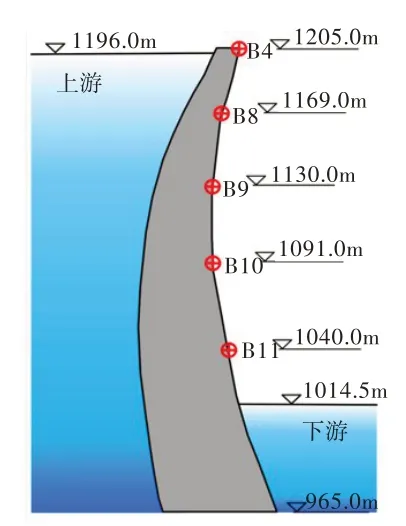
图4 拱冠梁测点布置

3.2 拱坝振动模态参数辨识基于EMD法对拱坝原型振动响应信号进行降噪处理，并引入信噪比（SNR）作为评价降噪效果的量化指标，计算结果如表2所示。从降噪效果来看，降噪后的信号具有更高的信噪比，典型测点降噪前后时程线（局部放大）如图6所示。以降噪后的信号为基础，采用奇异熵定阶的随机子空间法对拱坝振动模态参数进行辨识，识别结果如表3所示。以工况1为例，当信号阶次达到6时，奇异熵增量随阶次变化出现稳定（如图7所示），剔除特征值中非模态项和共轭项[22]，得到拱坝实际振动模态阶次为3阶；根据所识别的拱坝固有频率稳定图（如图8所示），可得该工况下拱坝前三阶固有频率分别为1.39、1.51和2.13 Hz。

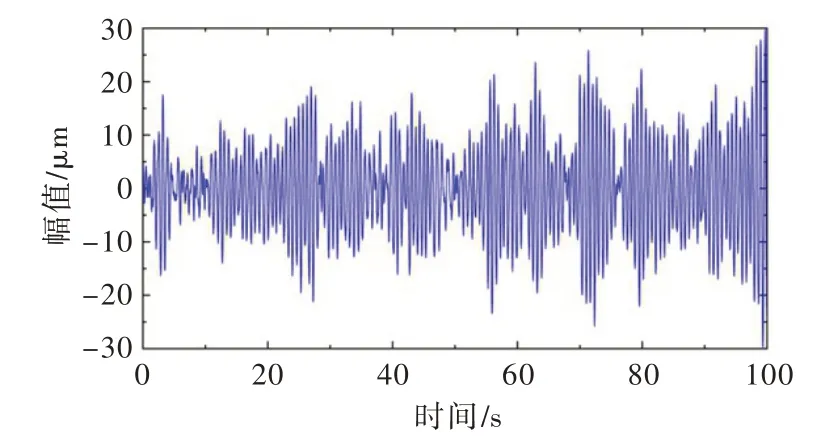
图5 工况1 下B5 测点原型振动响应时程

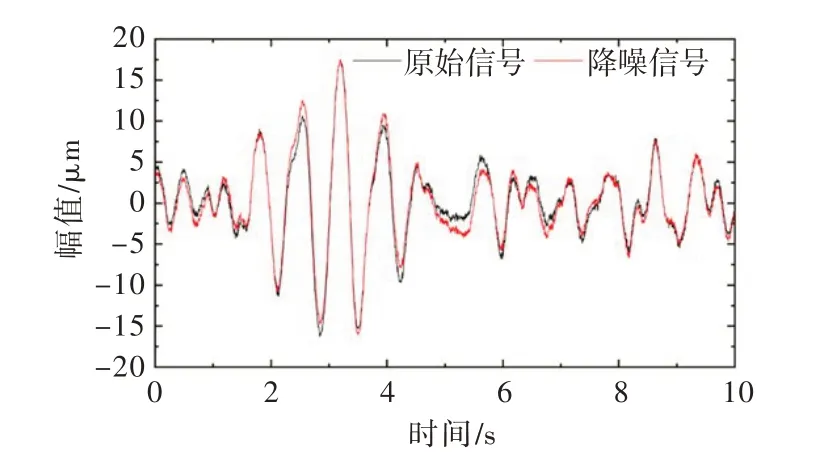
图6 工况1 下降噪前后B5 测点时程（局部放大）

表2 降噪前后信号指标对比 （单位：dB）

表3 拱坝振动模态参数识别结果

3.3 拱坝计算模型本文中响应面数学模型的确定是以拱坝有限元模型为基础。根据二滩拱坝混凝土的分区设计及大坝地质资料[23]，二滩拱坝及地基弹性模量的分区分别由3个坝体区域和5个地基区域组成，其中坝体区域编号分别为A、B、C，地基区域编号分别为D、E、F、G、H，其设计值如表4所示。本文运用ANSYS 有限元软件建立拱坝-地基-水体有限元模型，如图9所示，采用Fluid30 水体单元来模拟流固耦合效应，地基单元按照无质量弹性地基进行模拟，地基模拟范围为：深度取200 m，上游取424 m，下游取534 m，左、右坝肩取100 m；地基四周采用法向约束，底部采用固定约束。拱坝有限元模型共划分有282 049个单元和264 720个节点。

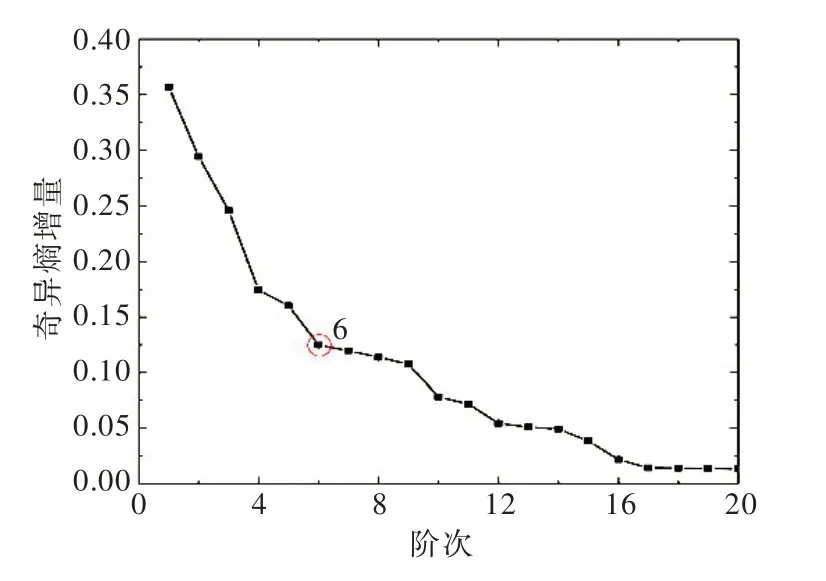
图7 工况1 下奇异熵增量随阶次变化

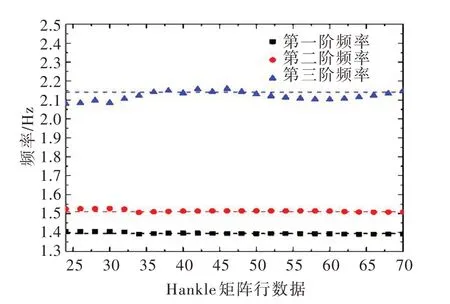
图8 工况1 下固有频率

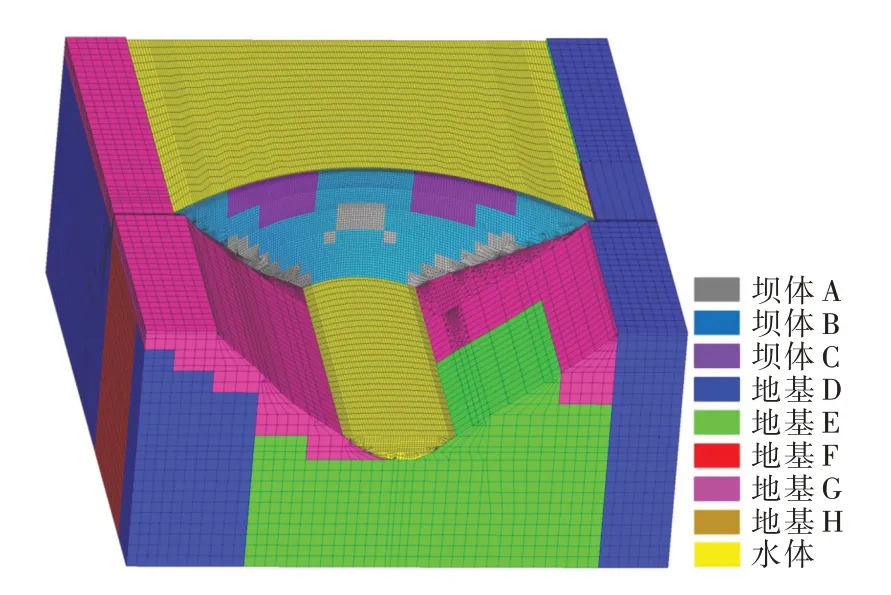
图9 拱坝-地基-水体有限元模型

表4 拱坝及地基弹性模量区域设计值

3.4 动弹性模量区域的敏感性分析以二滩拱坝及地基的8个弹性模量分区作为正交试验因素，根据各区域弹性模量设计值及文献[24-25]，确定拱坝及地基各动弹性模量区域的敏感性分析取值范围，并以其上、下限和设计值作为3个试验水平，如表5所示。根据正交试验因素和试验水平，形成了27 组动弹性模量区域敏感性分析的试验组合并进行有限元模态计算，得到各试验组合下的拱坝第一阶固有频率。

表5 动弹性模量试验水平 （单位：GPa）

表6 敏感性分析结果

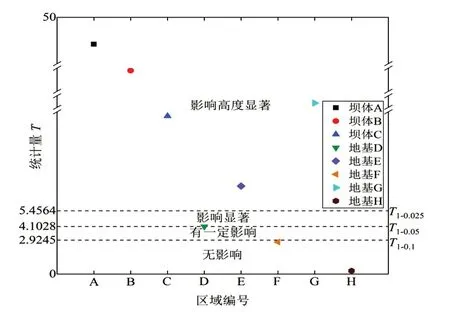
图10 动弹性模量区域显著性分析

基于方差分析法分析各试验组合下的拱坝第一阶固有频率，得出二滩拱坝及地基各动弹性模量区域对拱坝模态参数的敏感性分析结果，如表6所示。按统计量由大到小进行排序，可得到对拱坝模态参数敏感性由高到低的动弹性模量区域依次为A→B→G→C→E→D→F→H。根据统计量分布表[19]，得到T1-0.025=5.4564，T1-0.005=4.1028，T1-0.1=2.9245，如图10所示，可见对模态参数影响高度显著的区域为A、B、C、E、G，有一定影响的区域为D，无影响的区域为F和H。由此，本文确定待反演的动弹性模量区域为A、B、C、D、E和G 等6个区域。

3.5 响应面数学模型的构建根据所确定的待反演动弹性模量区域，采用拉丁超立方抽样法随机生成500 组动弹性模量样本集，参照各动弹性模量区域的敏感性分析取值范围，拟定A、B、C、D、E和G 共6个区域动弹性模量样本抽样区间分别为[28.34，42.5]、[27.37，41.05]、[26.4，39.6]、[28，42]、[20，30]、[16，24]（单位：GPa）。将500 组动弹性模量样本集输入拱坝有限元模型，计算动弹性模量样本集下所对应的500 组拱坝前三阶固有频率和振型，根据式（1）和式（2）拟合动弹性模量E与拱坝固有频率 fp及各测试节点归一化振型值φpq之间的响应面数学模型，并通过回归分析计算得到数学模型的待定系数和从而确定响应面数学模型，并以此替代有限元计算模型。

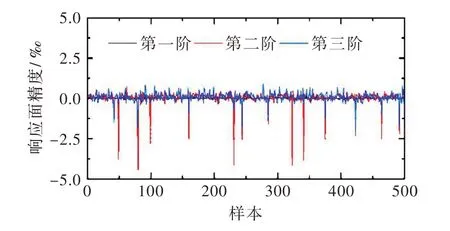
图11 频率响应面精度

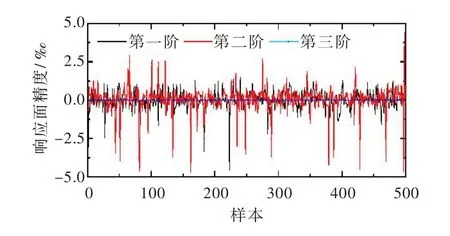
图12 B5 测点归一化振型系数响应面精度

根据式（3）计算得到各阶频率和典型测点（B5）归一化振型系数响应面精度均在5‰之内，如图11、图12所示。

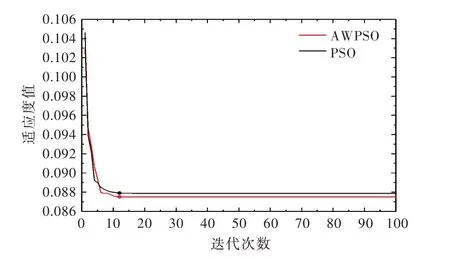
图13 粒子群优化算法对比

3.6 优化求解采用AWPSO 算法对二滩拱坝及地基动弹性模量反演的最优化数学模型进行迭代求解，结果如表7所示。同时与标准的PSO 算法适应度值的计算结果进行对比，如图13所示。从图13可知，两种算法都在第12 次迭代时收敛，但采用AWPSO 算法所得的适应值更小，具有更高的精度。

表7 动弹性模量反演结果

3.7 反演结果验证为验证反演结果的准确性，以工况2 作为验证工况，将动弹性模量反演结果输入拱坝有限元模型进行模态计算，并将模态计算结果与该工况下拱坝原型振动模态参数（前三阶固有频率和各测点归一化振型系数）识别结果相对比，如表8、表9所示。从对比结果来看，对于固有频率而言，计算结果与模态识别结果在数值上比较吻合，第一阶固有频率相对误差为0.29%，第二阶固有频率相对误差为0.76%，第三阶固有频率相对误差为2.05%。对于拱坝测点归一化振型系数而言，大部分测点识别值和计算值之间的相对误差都在10%以内；少部分测点的相对误差稍大，如第一阶B2 测点的相对误差为10.75%，第二阶B6 测点的相对误差为-10.38%，主要是由于位于坝肩的测点振幅较小，受噪声干扰大，导致振型识别存在一定误差。总体上，基于动弹性模量反演结果的拱坝计算模态参数与原型振动模态参数吻合较好，该方法的反演结果是合理可靠的。

表8 拱坝前三阶固有频率对比

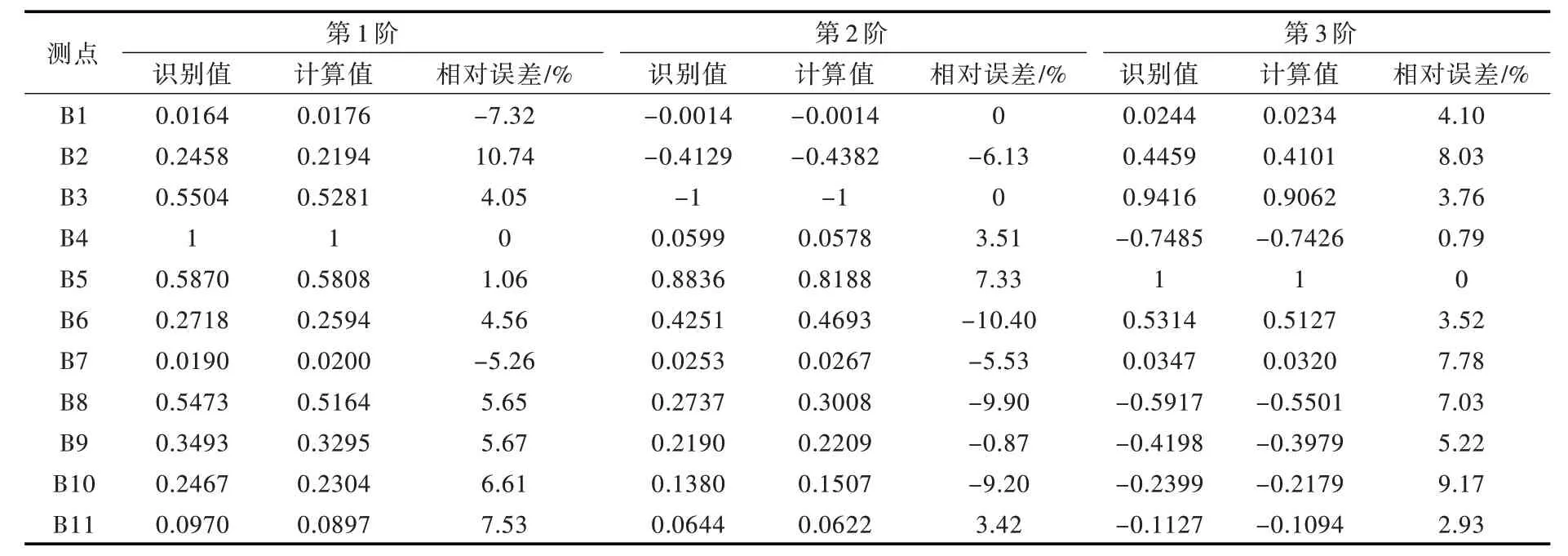
表9 拱坝测点归一化振型系数对比

4 结论

本文提出了基于敏感性分析与粒子群算法的拱坝原型动弹性模量反演方法，主要结论如下：（1）构建了描述拱坝及地基分区动弹性模量与拱坝模态参数之间非线性映射关系的响应面数学模型，基于正交试验法深度挖掘了各动弹性模量区域对拱坝模态参数的敏感性，提高了动弹性模量反演的计算效率。（2）提出了基于响应面数学模型计算模态参数和拱坝原型振动模态参数之间相对误差的目标函数，建立了拱坝及地基分区动弹性模量反演的最优化数学模型，将动弹性模量反演问题转换成目标函数最优化求解问题。（3）利用AWPSO 算法对最优化数学模型进行寻优，克服了PSO 搜索精度不高的不足，具有更好的适用性。工程实例验证结果表明，该方法是合理可靠的，可为拱坝动弹性模量反演提供一条新思路。