基于MacCormack格式的变网格瞬变流模拟

万五一，陈潇逸，张永进

（1.浙江大学 水利工程学系，浙江 杭州 310058；2.浙江省水利水电勘测设计院，浙江 杭州 310002）

1 研究背景

水锤现象可以导致管道的压力振荡，造成爆管和压扁等危害。在有压管路系统中，阀门的突然启闭、水泵的事故停机、水轮机导叶的骤然启闭等均能引起压力与流量的急剧变化，从而导致水锤危害的发生。如何模拟、预测和控制水锤是目前水力学研究领域的热点问题之一[1-3]。水锤的模拟对防止管道的水锤危害与保障管道的安全运行至关重要。随着计算机技术的发展，不同的数值方法被用于输水管路的水锤模拟，主要有特征线法（MOC）[4]、有限元法[5]、有限体积法[6]等。在此基础上，国内外的学者对水锤数值计算方法不断进行改进，也将一些新的数值方法引入到水锤模拟中。耿艳芬等[7]采用特征分解构建了一阶和二阶Godunov 格式的水锤计算模型，并通过通量限制和重构获取了高精度的格式。赵修龙等[8]建立了Crank-Nicolson 格式的水锤离散方程，该格式具有二阶精度且稳定性好。刘韩生等[9]将高分辨TVD 格式引入水锤方程的求解中，该格式具有精度高、耗散低、不产生数值振荡等优点。Kim[10]提出采用脉冲响应法模拟配水系统的瞬变流，并提出了一种考虑层流与湍流过渡的修正方法。Budinski[11]采用了格子玻尔兹曼方法求解管道瞬变流问题，该方法具有不受MOC网格限制与计算效率高的优点。

尽管如此，MOC 仍为目前最常用的水锤数值计算方法之一，其具有计算简洁、易于编程、可处理复杂系统等优点，广泛地运用在水力发电[12]、油气输运[13]、核能发电[14]等各个领域的瞬变流模拟研究。但MOC 通常需要采用规则的网格，且空间步长与时间步长受到特征线的严格限制。在解决特定的复杂管路系统问题时，需要通过调整波速、改变管长或插值等方法来满足不同管道的相同时步要求。若系统中连接有一段很短的管道，则所有管道需要选取很短的时间步长以满足同步，可能需要较大的计算时耗[4]。

MacCormack格式是一种求解可压缩流体流动问题的有限差分格式，在时间和空间上具有二阶精度[15]。该方法具有易于理解，便于实现的优点[16]，在计算流体力学中广泛地应用于Navier Stokes 方程的求解[17-20]。但是MacCormack格式目前在瞬变流的数值模拟中运用的相对较少。Chaudhry 等[5]简要介绍了采用MacCormack格式对水锤的拟线性双曲型偏微分方程的求解过程。Amara[21]将MacCormack格式引入摩擦管道的水锤数值计算中，但仍基于特征线法建立了边界条件，从而无法对网格中的时间步长与空间步长进行单独设定。王勇等[22]基于MacCormack格式建立了长输液体管道的水力瞬变模型，并分别采用了MOC方法和线性外插法对边界条件进行处理。在我们之前的研究中，提出了基于MacCormack时间推进格式的水锤计算模型（MTMS）[23]。与常规的MOC 相比，该模型突破了网格划分中时间步长与空间步长相互制约的局限，具备网格划分灵活的优点，但其仍然采用了统一的空间步长。

为了分析包含短管情况下的变特性复杂管路系统中的水锤，拓展变空间步长情况下的同步水锤模拟方法，本文通过MacCormack格式建立了变空间步长水锤求解模型（V-MCS）及相应的边界条件，对变特性管路系统中的水锤现象进行了数值模拟。在V-MCS方法中采用了变空间步长的不规则离散网格，该网格不再受特征线的约束，其空间步长的选取只需满足Courant-Friedrichs-Lowry（CFL）准则的要求，在变特性复杂管路系统中，该方法克服了为保证与短管时间步长一致而需采用较密计算网格的问题。通过规则网格的MOC方法与MTMS方法对V-MCS方法的模拟结果进行了验证与分析，本文提出的V-MCS方法对变特性复杂管路系统的水锤数值模拟具有较好的参考价值。

2 数学模型

2.1 基本控制方程描述管道有压流的基本控制方程包括了连续方程和运动方程[4]，其矩阵形式可写为：

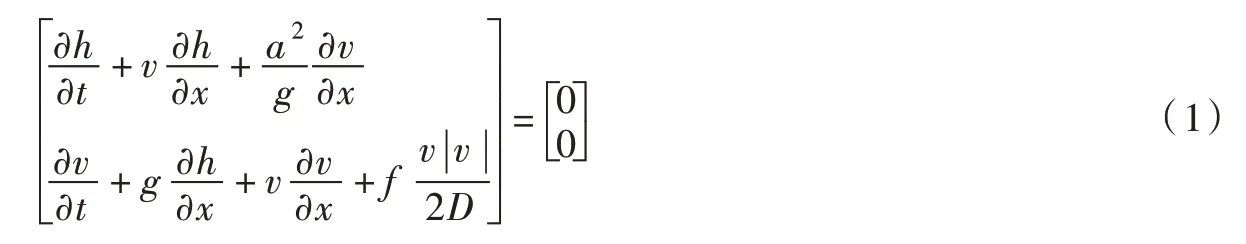
式中：h为测压管水头；t为时间；v为流速；x为节点位置；a为水锤波速；g为重力加速度；f为摩阻系数；D为管道直径。

式（1）包括了一对准线性双曲线偏微分方程，包含了测压管水头h和流速v 两个因变量，为便于利用MacCormack格式进行偏微分方程离散与因变量求解，将基本控制方程改写为：

在使用MOC模型求解时，通常将摩阻系数f 近似为恒定摩阻系数来考虑。为提高计算精度，本文采用Brunone模型[24]在控制方程中引入非恒定摩阻。Brunone模型中考虑了瞬时当地加速度和对流加速度对非恒定摩阻的影响，改进后的表达式为[25]：

式中： fq为恒定摩阻系数；k为Brunone 摩擦系数。

采用Vardy的剪切衰减系数C*对Brunone 摩擦系数k进行计算[26]：

式中： Re为雷诺数。结合式（2）和式（3）可得控制方程转化后的形式为：

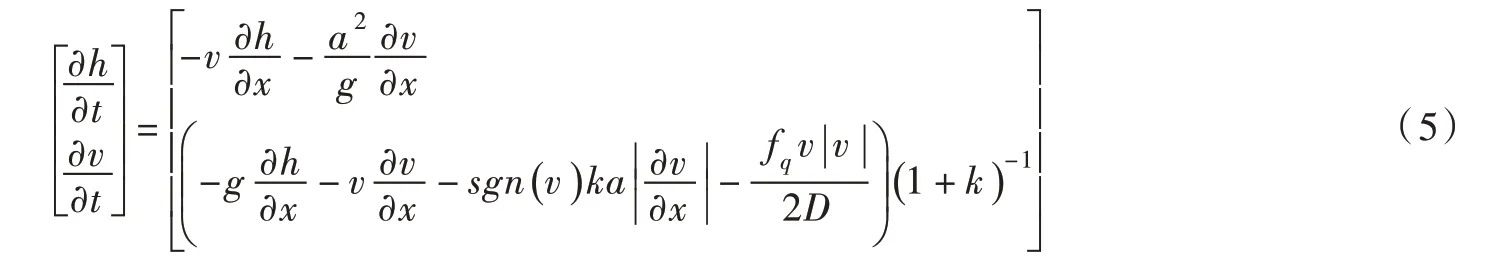
2.2 基于变空间步长的MacCormack 格式的水锤模型图1为变空间步长的x-t 计算网格划分，其中ns为管道的网格划分节点数。在MacCormack格式中，时间步长∆t与空间步长∆x 不受特征线约束条件∆x=a∆t的限制，可对网格进行更加灵活的划分或修改。MacCormack格式的约束条件为CFL（Cou⁃rant-Friedrichs-Lowry）准则，表达式为[16]：

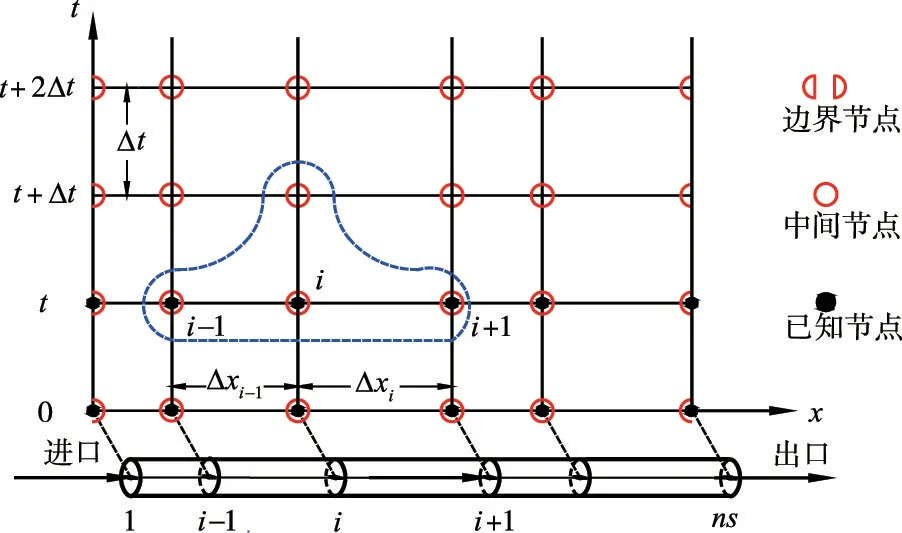
图1 变空间步长的计算网格划分

因此，将网格中的空间步长取为满足CFL 准则条件下的任意值∆xi，i=1，2，…，ns-1。如图1所示，节点i-1与节点i之间的空间步长为∆xi-1，节点i与节点i+1之间的空间步长为∆xi。假设t时刻的节点均为已知，利用MacCormack格式的预测校正二步法进行时间推进，求解出t+∆t时刻各个节点的和。首先在预测步中对空间导数进行向前差分，将t时刻节点i的时间导数写为：

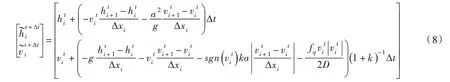
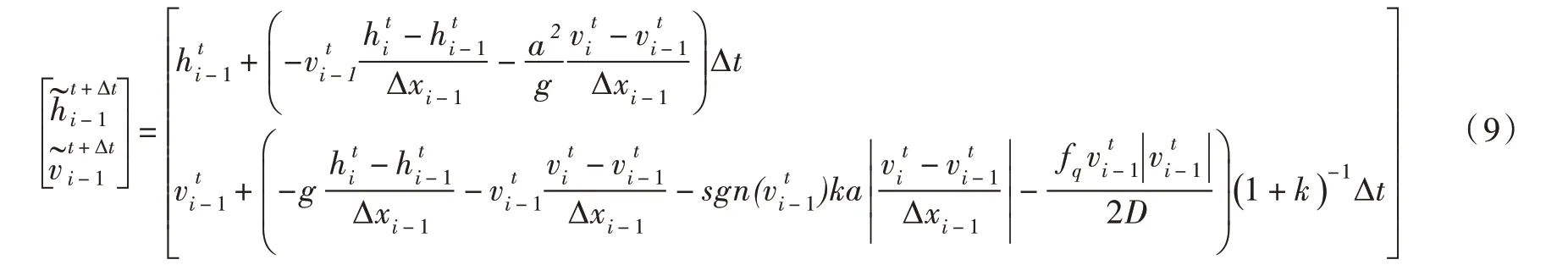
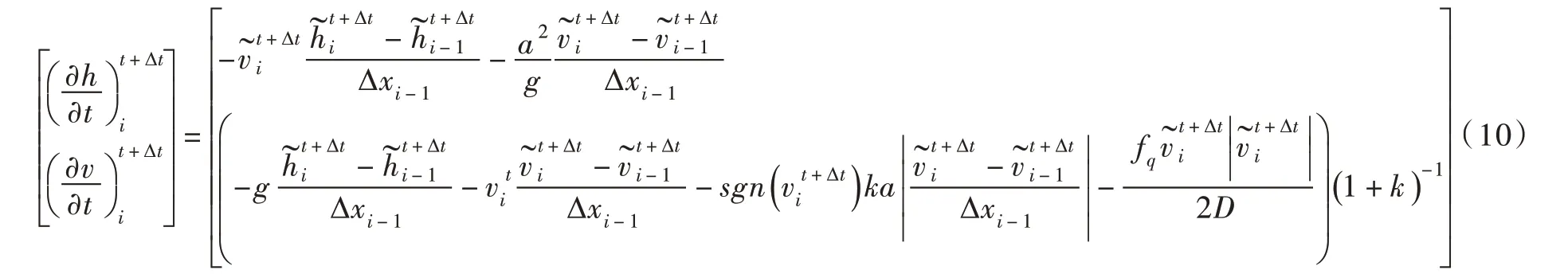
作为校正，结合式（7）和式（10）得到空间导数平均值为：

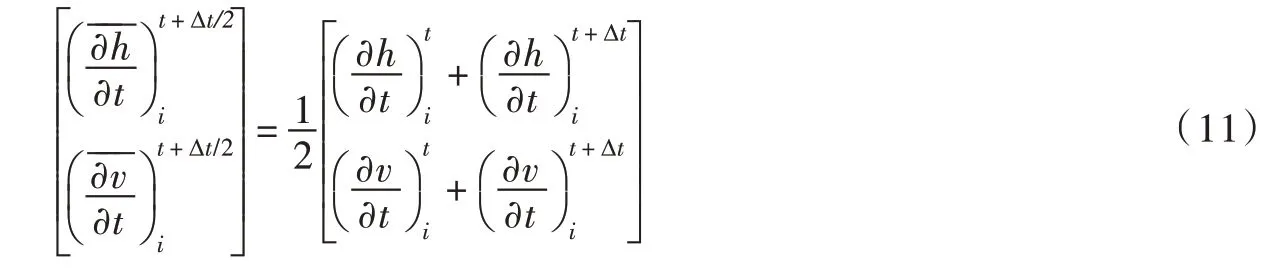
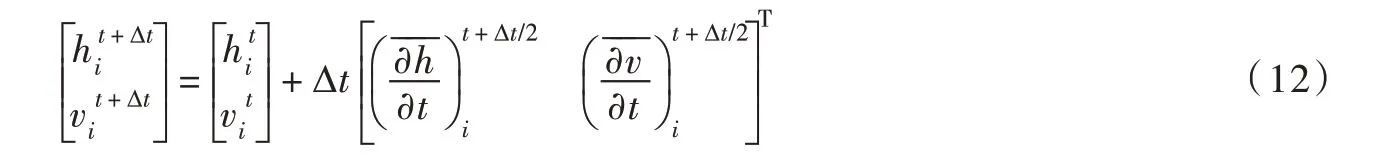
式（12）为基于MacCormack格式的变空间步长水锤计算模型，适用于网格中t+∆t时刻所有中间节点的求解。在该模型中采用了变空间步长的不规则离散网格，空间步长可在满足CFL 准则的前提下进行选取。由于预测校正二步法中，在预测步向前差分，在校正步向后差分，因此该格式具有二阶精度。由于该模型中包含了对流加速度项，考虑了流速对水锤波速的影响。此外，该模型采用非恒定摩阻项，有利于更准确地模拟水锤波的衰减过程[27]。

2.3 边界条件

2.3.1 进口水库边界条件 在输水管路系统中，管路进口端通常与水库相连，在短时间内，可认为上游水库水位为恒定。因此管路进口端水库的限制条件为：

整理得，进口水库边界的求解模型为：

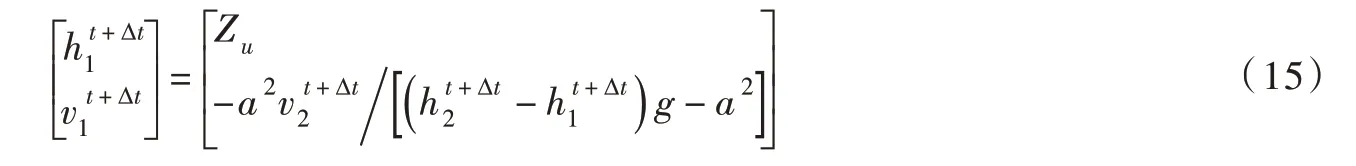
2.3.2 调压井边界条件 调压井是输水管路中重要的水锤防护设备，调压井边界条件中的连续微分方程可表示为：

式中：Qu为调压井上游流量；Qd为调压井下游流量；Z为调压井水位；Aw为调压井断面面积。

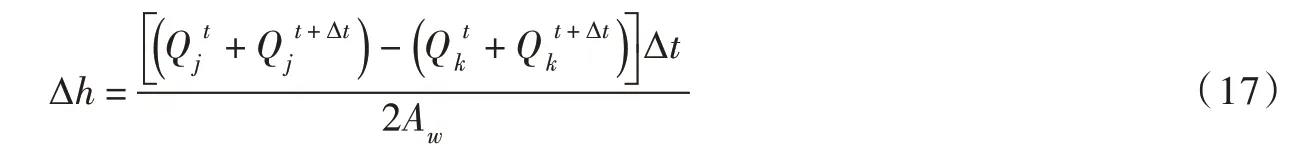
式中，j、k分别为与调压井上游和下游相邻的管道节点。

对式（17）采用向前差分[28]，并结合式（5）进行整理后得到调压井边界的求解模型为：

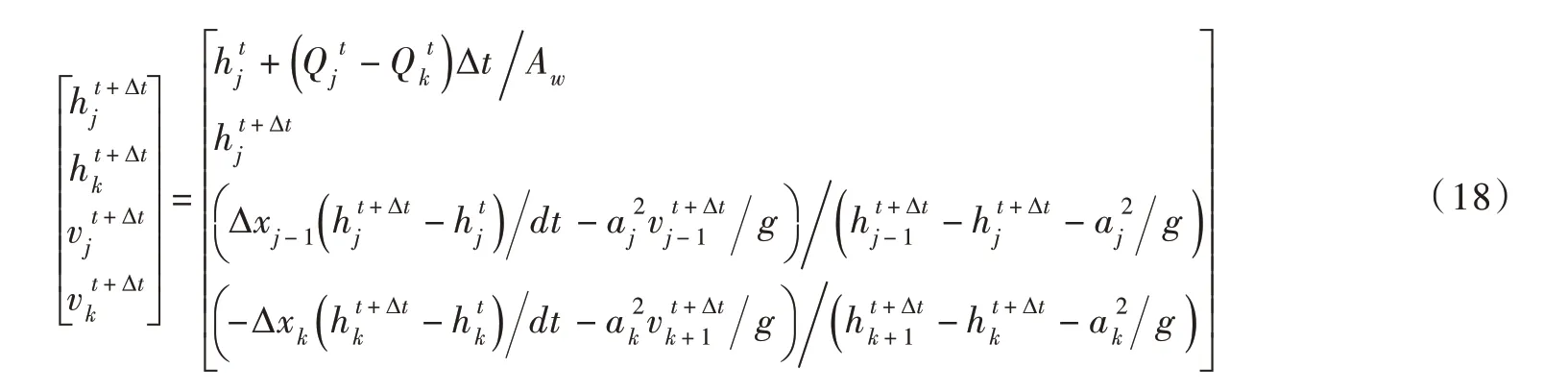
2.3.3 出口阀门边界条件 输水系统出口为控制阀门，通过该阀门可对输水线路的流量大小进行调节，阀门的关闭可导致输水线路中水锤现象的发生。出口端的可通过线性外插方法计算得出，可根据已计算出的及阀门孔口方程得到，因此出口边界条件可写为：

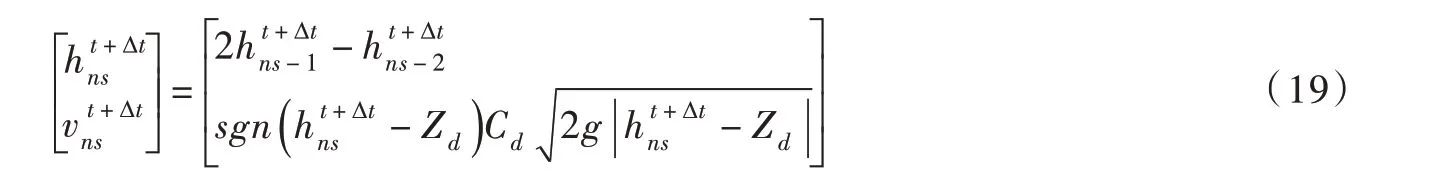
式中Zd为阀门下游水位。当阀门完全关闭后，管道出口端的流速限制条件为：

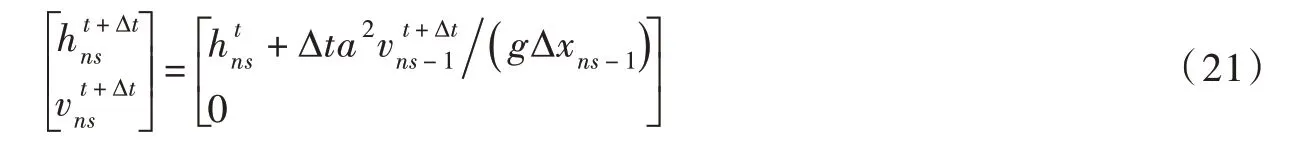
根据上述提出的基于MacCormack格式的变空间步长水锤模型及边界条件，从已知时刻t 开始时间推进，可求出t+∆t，t+2∆t，…，t+n∆t 等各个时刻所有节点的水力参数。

3 模型验证

为了对本文提出的V-MCS 水锤计算模型及边界条件进行验证，分别采用V-MCS方法、MOC方法及MTMS方法对常规的水库-管路-阀门（RPV）输水系统的水锤过程进行模拟。在RPV系统中，管道长度L为1000.0 m，直径D为0.5m，波速a为1000.0 m/s，糙率系数n为0.012。管道进口端水库水位Zu为30.0 m，管道的初始流量Q0为0.18m3/s。管道出口端阀门关闭时间Tc为4 s。其中MOC方法采用规则网格，时间步长∆t为0.01 s，空间步长∆x为10.0 m，网格分段数为100 段，MTMS方法也采用与MOC方法相同的规则网格。而V-MCS方法采用变步长网格，时间步长∆t为0.01 s，在满足CFL准则的基础上将空间步长取为10.0 m≤∆x ≤30.0 m 范围内的随机数，管道分段数为45 段。为了验证V-MCS方法的正确性，将其与MOC方法和MTMS方法的水锤压力波动过程模拟结果进行比较。如图2与图3展示了采用三种不同方法计算的RPV系统的水锤压力波的波动过程，结果表明，三种不同方法计算得到的管道中点与末端的压力波动曲线基本重合，压力波的振幅大小吻合良好，验证了V-MCS方法在水锤计算中的准确性。

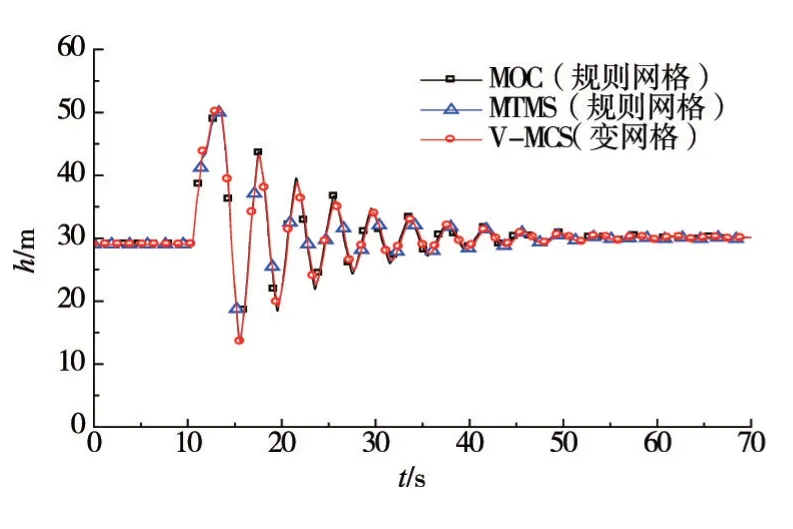
图2 管道中点水锤压力波动过程模拟结果对比

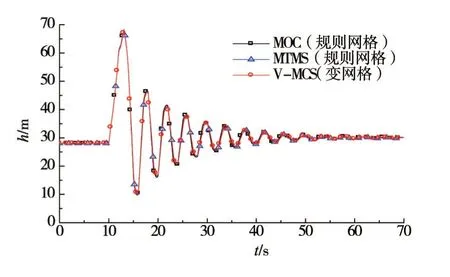
图3 管道末端水锤压力波动过程模拟结果对比

4 案例分析

4.1 初始条件在实际输水工程项目中，输水线路通常距离较长，管线根据地形变化而常有起伏，管道的材质也常有差异，因此在运行调度过程中的水力条件相对复杂。水锤数值模拟的目的主要是预测系统中可能出现的压力与流量波动情况，获得管道的薄弱节点及出现的水锤极值压力，为工程设计与运行提供参考。在案例分析将本文提出的V-MCS方法应用于输水工程管路系统的水锤模拟中，进一步地对水锤模拟结果进行分析与讨论。

如图4所示为变特性输水管路系统示意图，其中上游水库水位Zu为56.5 m，下游水厂水池的水位Zd为22.0 m。管路总长度为24.16 km，由DN2400 输水隧洞与DN1800 钢管组成，沿线设置4 座通气井与1 座调压井，管线的基本参数如表1所示。管道末端阀门关闭时间Tc为30 s，管线的流量由4.20 m3/s 减小至0 m3/s，最大计算时刻为10 800 s。本文基于V-MCS方法对该管路系统的水锤过程进行模拟与分析，并采用MOC方法和MTMS方法与其模拟结果进行对比。

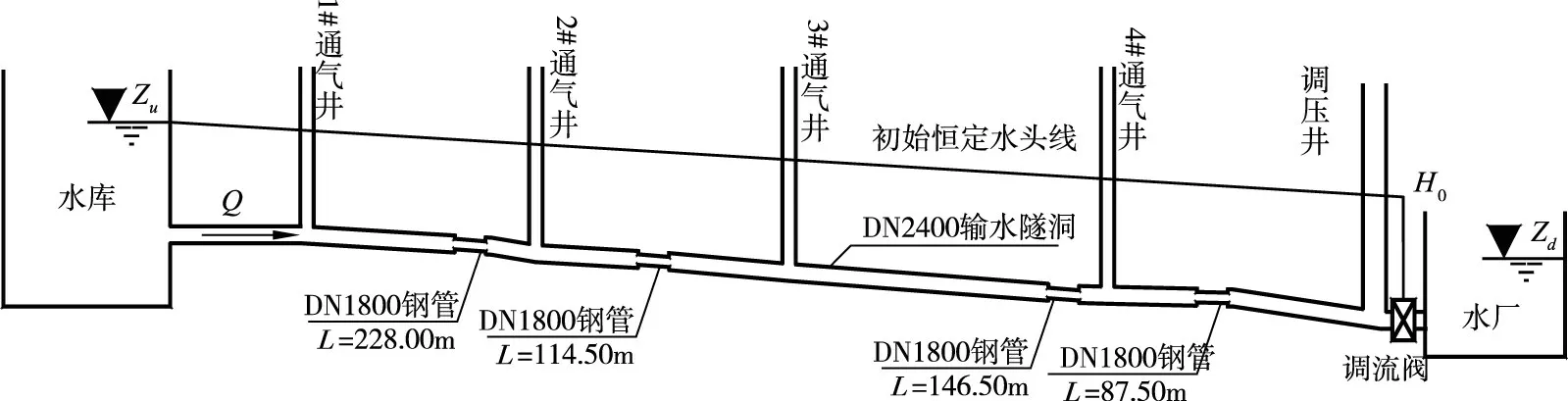
图4 变特性输水管路系统示意图

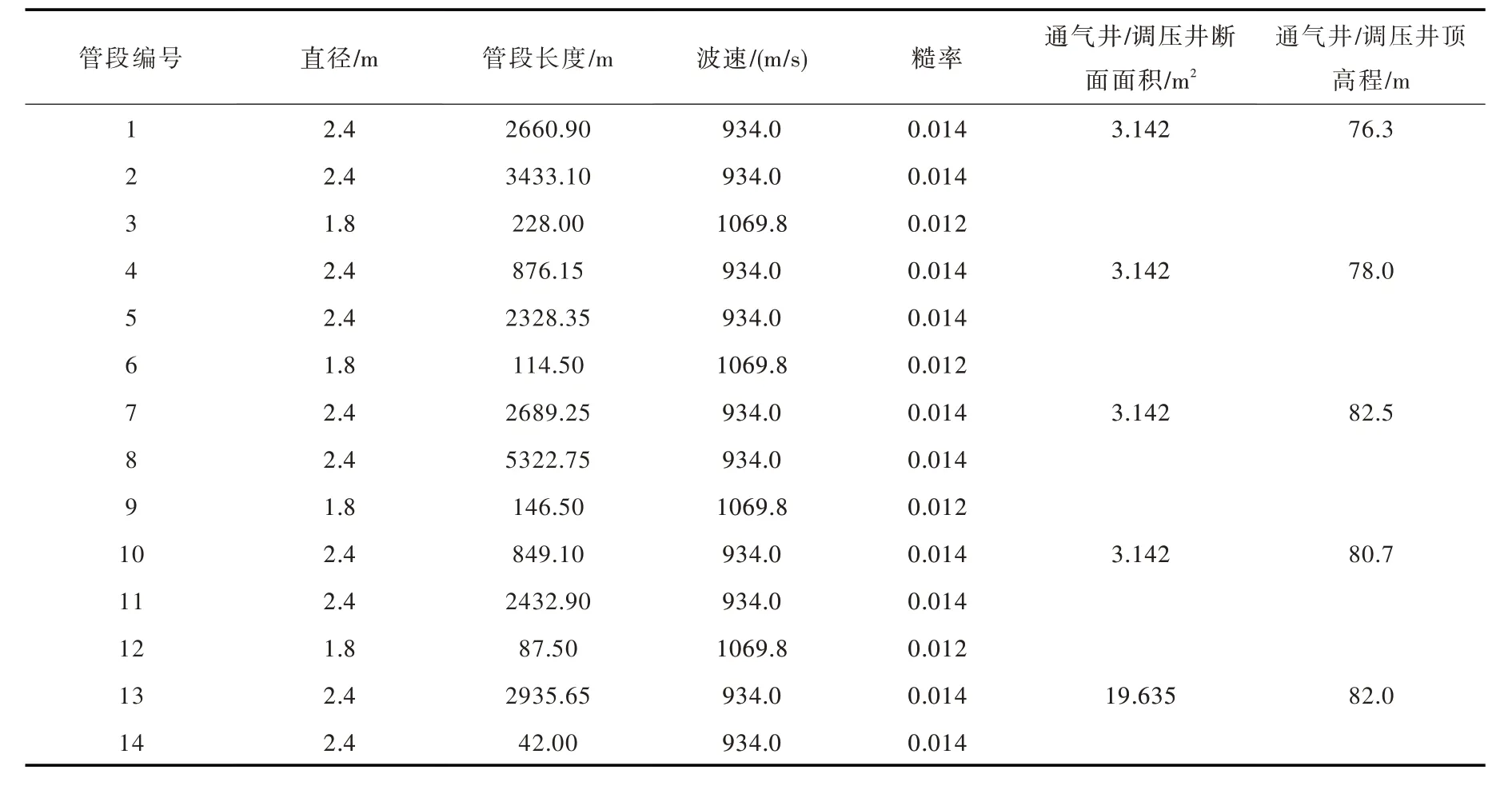
表1 输水管线基本参数

4.2 模拟与分析在采用MOC方法和MTMS方法进行管道的网格划分时，先选定时间步长再根据∆x=a∆t 确定空间步长的大小。为满足网格的分段数为整数的要求，对波速a进行细微调整，则调整后的波速a′为：

通常情况下，时间步长越小，调整后的波速与实际波速越接近，在本例中，当时间步长取为0.01 s时，偏差最大的波速为1040.9 m/s，偏差为2.7%。MOC方法和MTMS方法中管道的总分段数为2343 段。而采用V-MCS方法进行变网格划分时，空间步长不再固定，可根据计算需求对空间步长进行选择性划分。如表1所示，第6、9、12、14 号管段长度小于200 m，对这些短管的空间步长∆x 仍取为a∆t，而将管路其余部分的空间步长取为a∆t ≤∆x ≤12.0 m 范围内的随机数，管路总分段数为2217 段。

图5—图7为采用V-MCS方法对算例中管路系统的水锤过程进行数值模拟的结果。图5为基于V-MCS方法得到的阀前水锤压力波动过程。由图5可知，由V-MCS方法得到的水锤极值压力大小与MOC方法、MTMS方法的模拟结果相同。阀前的水锤压力最大值为75.40 m，水锤压力最小值为42.25 m。随着时间推进，由V-MCS方法与MTMS方法模拟得到的水锤压力波衰减过程与常规MOC方法相比出现了微小偏差，其原因在于V-MCS方法与MTMS方法中均考虑了非恒定摩阻的影响。图6所示为阀前流量变化过程，基于V-MCS方法得到的流量变化过程与其余两种方法得到的模拟结果一致。

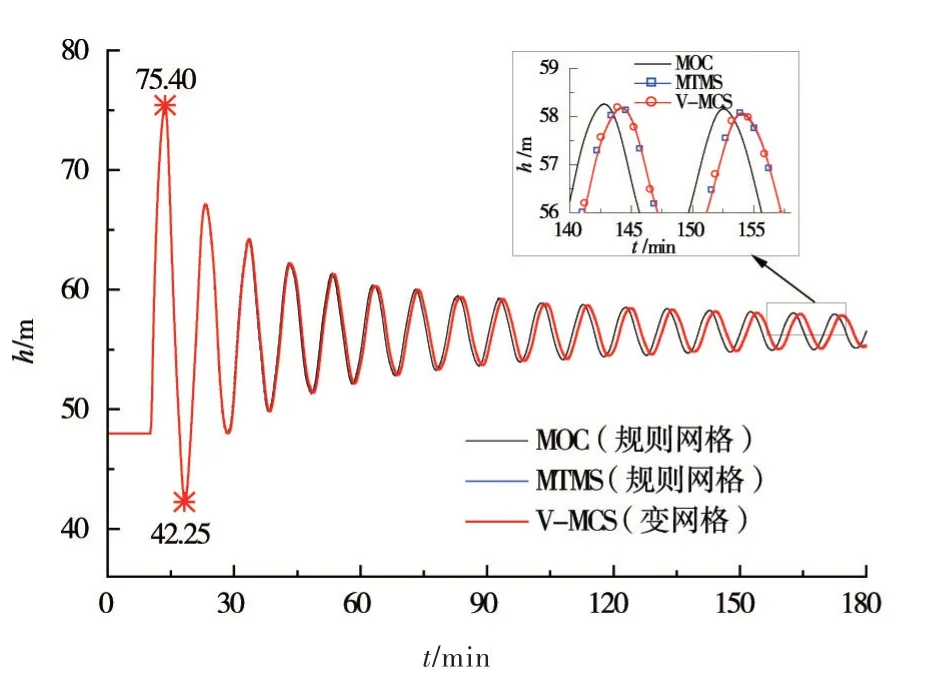
图5 阀前压力波动过程

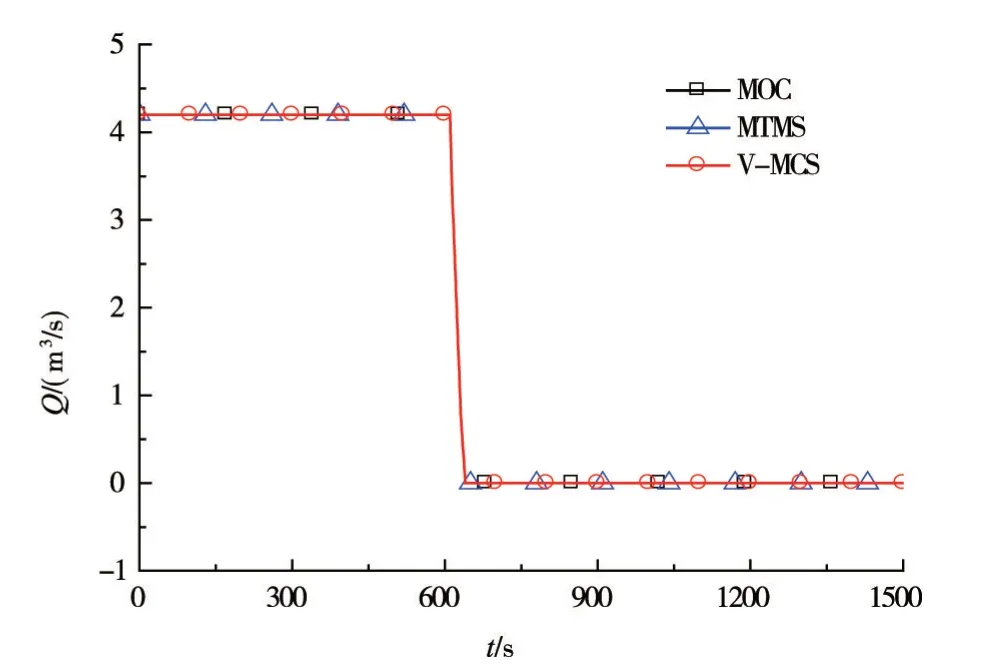
图6 阀前流量变化过程

图7所示为基于V-MCS方法和MOC方法的管道沿线极值压力分布情况。图中蓝色线为管道初始恒定水头压力线，红色线为最大压力包络线，绿色线为最小压力包络线。由图7可知，管道最小压力包络线始终位于管道中心线高程以上，管道全线无负压现象发生。管道最大内水压力为68.90 m，位于管道阀前位置。基于V-MCS方法得到的水锤极值压力与MOC方法得到的极值压力包络线吻合良好。

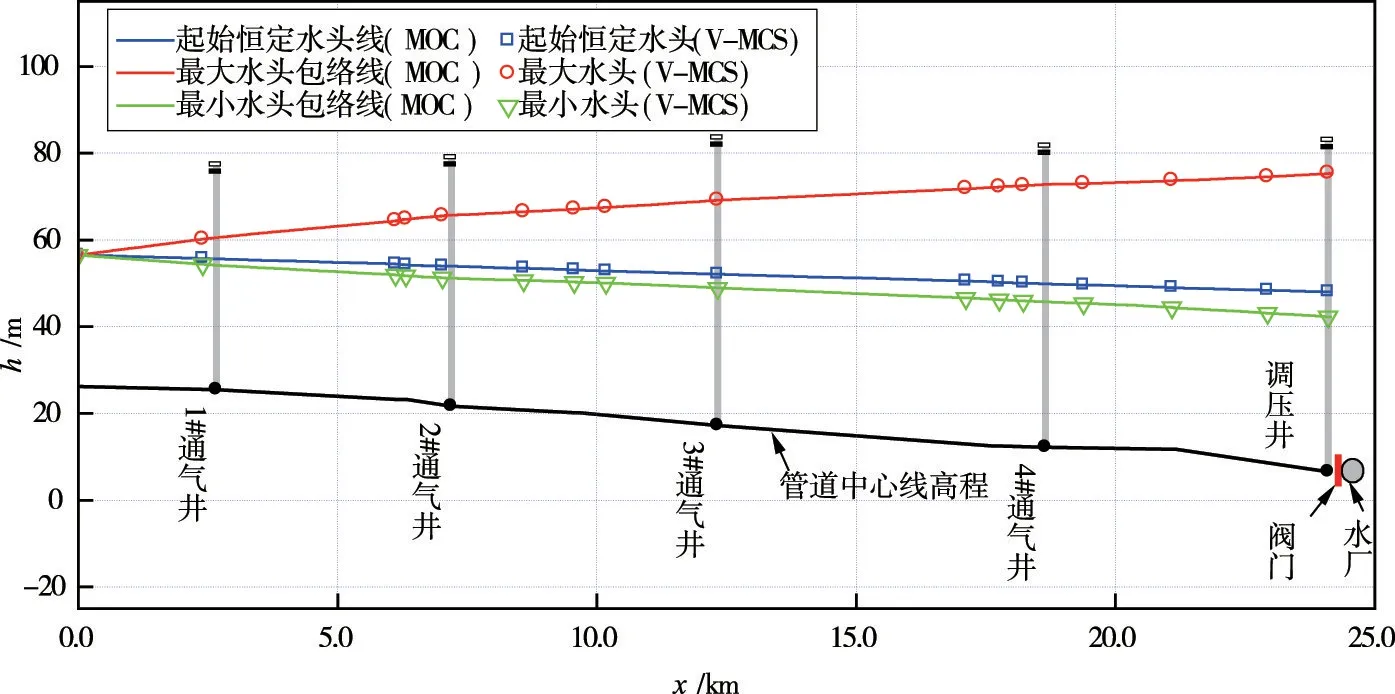
图7 管道沿线极值压力分布

图8 不同分段数下的阀前压力波动过程对比

表2 V-MCS与MOC 模拟结果对比

为了分析管道分段数对模拟结果的影响，图8对不同分段数情况下的阀前压力波动过程进行了比较。如图8所示，随着V-MCS方法空间步长取值范围的增大，管道分段数随之减小，位于第一相的水锤极值压力大小基本一致。但选取的空间步长范围过大时，对水锤波衰减过程的准确模拟有所影响。将V-MCS方法与MOC方法的计算结果整理于表2，其中无量纲时间Ct为V-MCS方法与MOC方法计算耗时的比值。比较两种方法的Ct可知，在步长相当的情况下，由于V-MCS的单步计算更为复杂，与MOC方法相比计算耗时更长。由于V-MCS中的空间步长可以进行调整，在保证时间步长不变的情况下，通过增大空间步长可以较大程度减小总的计算耗时。由于在水锤模拟中，线路中的压力极值是计算中尤为关心的问题，因此在采用V-MCS方法时可适当地减少管道分段数来缩短计算耗时。如需获得精确的水锤压力波动衰减过程，则可通过增加管道分段数来提高计算的精度。

4.3 讨论模拟结果表明，本文提出的V-MCS方法可有效地得到管道水锤的模拟结果。V-MCS方法具有时间空间上的二阶精度，计算结构清晰，易于编程实现。V-MCS方法具有以下优点。首先，在模型建立中保留了控制方程中的对流加速度项，将管道流速对水锤波传播的影响考虑了进来，可为高流速情况下的水锤模拟提供参考。在模型中考虑了非恒定摩阻，能够较好地反映摩阻对水锤波的衰减过程的影响。其次，在网格划分上，MOC方法采用了固定的离散网格，且时空步长受到特征线路径的严格约束。但V-MCS方法采用了不规则的离散网格，根据计算需求调整网格的空间步长大小，突破了时空步长一一对应的限制。因此V-MCS方法可以有针对性地仅对管道薄弱区域或控制节点进行详细划分，相比MOC方法减少了管道全线的总分段数。此外，对于复杂管网系统，V-MCS方法可以方便地对不同的管道选取不等的空间步长，而无需进行波速调整或插值，从而有利于对复杂系统中的各种管道进行同步求解。但在V-MCS方法中若选取的空间步长过大，对水锤压力波动衰减过程的准确模拟有所影响。而且，由于V-MCS方法将原有的固定步长根据需要改成了特定的步长，在数值计算中可能一定程度上增加了数值编程的难度。

5 结论

建立了基于MacCormack格式的变空间步长水锤计算模型（V-MCS），在模型中采用了变空间步长的离散网格，空间步长可在满足CFL 准则的基础上进行选取。此外，结合线性外插法建立了与模型相匹配的边界条件。

通过与MOC方法及MTMS方法模拟结果的对比，对提出的V-MCS方法及相应边界条件进行了验证。验证结果表明，V-MCS方法可以有效地对管道水锤过程进行模拟，其模拟结果与MOC方法及MTMS方法的模拟结果吻合良好。

采用V-MCS方法对变特性复杂管路系统的水锤现象进行了模拟与分析，结果表明，V-MCS方法可以准确地模拟出控制节点的水锤极值压力大小。由于在模型中考虑了非恒定摩阻的影响，从理论上讲，得到的水锤压力波衰减过程模拟结果与实际更为接近。基于V-MCS方法得到的极值压力与常规方法得到的极值压力包络线吻合良好。

在包含短管等特定的变特性管路中，V-MCS方法可以根据计算需求对不同管道选取不等的空间步长，减小网格分段数以此节约计算时间。因此，V-MCS方法有利于对复杂管路系统的水锤求解进行同步运算，对输水工程管路系统的水锤数值模拟具有一定的实际意义。