活用直线系 巧解直线方程

■姜 艳

所谓“系”方程,就是具有某种共同特征或性质的曲线,其方程可用一种统一的方程形式来表示,其实质就是参数法,即设而不求、整体思想的具体应用。灵活运用“系”方程,解决直线问题,可以简化运算、降低难度,提高解题效率。

一、直线系方程的常见类型

(1)过定点的直线系:直线y-y0=k(x-x0)(k 为参数)表示过定点(x0,y0)的直线系,特别地,当斜率k 不存在时,直线x=x0过定点(x0,y0)。直线y=kx+b(k为参数,b 为常数)表示过定点(0,b)的直线系,特别地,直线x=0过定点(0,b)。(2)定斜率的直线系:直线y=kx+b(k 为常数,b为参数)表示斜率为k 的互相平行的直线系。平行于已知直线Ax+By+C=0 的直线系方程是Ax+By+λ=0(λ 是参数且λ≠C);垂直于已知直线Ax+By+C=0 的直线系方程是Bx-Ay+λ=0(λ 是参数)。(3)过两直线交点的直线系:过两条已知直线l1:A1x+B1y+C1=0和l2:A2x+B2y+C2=0的交点的直线系方程是A1x+B1y+C1+λ(A2x+B2y+C2)=0(λ∈R,但不包括l2)。

二、直线系方程的应用

例1 已知直线方程为(2+m)x+(1-2m)y+4-3m=0。求证:不论m 为何实数,直线过定点。

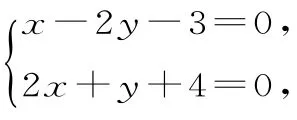
例2 已知直线l1与直线l2:x-3y+6=0 平行,l1能和x 轴、y 轴围成面积为8的三角形,请求出直线l1的方程。

例3 求经过点A(2,1),且与直线2x+y-10=0垂直的直线方程。

解：因为所求直线与直线2x+y-10=0垂直,所以设该直线方程为x-2y+c=0。又直线过点A(2,1),所以2-2×1+c=0,解得c=0。故所求直线方程为x-2y=0。

例4 已知两条直线l1:x-2y+4=0和l2:x+y-2=0的交点为P,求过点P 且与直线l3:3x-4y+5=0垂直的直线l的方程。

解：(方法1)设所求直线l 的方程为4x+3y+c=0。由l1与l2组成的方程组可得到交点P(0,2),将其代入方程可得c=-6。故直线l的方程为4x+3y-6=0。

(方法2)设所求直线l 的方程为x-2y+4+λ(x+y-2)=0,即(1+λ)x+(λ-2)y+4-2λ=0。因为直线l 与l3垂直,所以3(1+λ)-4(λ-2)=0,可得λ=11,所以直线l的方程为4x+3y-6=0。

例5 已知三角形三边所在的直线方程分别为2x-y+4=0,x+y-7=0,2x-7y-14=0,求边2x-7y-14=0 上的高所在的直线方程。