南京长江大桥桥头堡抗震加固受力性能研究
2021-01-04华一唯
华一唯,淳 庆
(东南大学建筑学院,江苏南京 210096)
0 引 言
南京长江大桥桥头建筑为复式桥台,具有重要的历史、艺术和科学价值。2016—2018年,南京长江大桥进行了一次历时27个月的大修,其中对南京长江大桥桥头堡的填充墙水磨石墙裙以上部分进行了单面聚合物砂浆-钢丝网加固。本工作将研究这种特殊的填充墙加固方式对南京长江大桥桥头堡抗震性能的影响。
目前,填充墙对结构抗震性能的影响已有一部分研究,不少学者提出如等效斜撑模型[1]、填充墙元模型[2]、三支杆模型[3]等以考虑填充墙的结构效应,同时还有一些学者进行了有限元[4-6]及试验研究[7-8]。但以上模型均针对未开裂的、未加固的填充墙。针对填充墙加固后对结构的影响的研究很少,蒋利学[9]通过试验,研究了加固后的填充墙对原框架结构抗震性能的影响,但仅停留在单层框架。考虑填充墙加固或开裂后结构效应的建模方法研究更是很少涉及。
为此,提出考虑填充墙加固后刚度增强效应的桥头堡建模方法。同时,基于传统斜撑模型,提出一种新的斜撑模型以考虑罕遇地震工况下填充墙体开裂的影响。接着,利用上述模型建立填充墙加固前后的桥头堡有限元计算模型,并选取国外地震波与该地区经历的真实地震波各1条作为地震激励,分析填充墙未加固以及加固对桥头堡抗震性能的影响,同时考察2种地震波激励结果的差异。
1 考虑填充墙加固及开裂的简化模型
讨论填充墙等效斜撑模型的适用性,针对罕遇地震下填充墙开裂情况提出一种新的斜撑模型。并对原有的等效斜撑模型进行修正,以考虑聚合物砂浆加固所带来的刚度增强效应,以研究填充墙加固后对桥头堡抗震性能的影响。
等效斜撑的概念由Holmes[10]于1961年首次提出,Holmes基于沿对角线方向加载试件破坏机理的分析,认为填充墙的作用如同桁架系统中的对角压杆,在侧向水平力作用下,框架和填充墙之间的应力只在填充墙的受压区边界互相传递。根据填充墙与梁和柱的接触长度αh、α1,就可以估计斜撑的宽度w[1]:
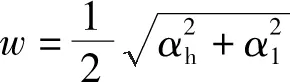
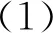
但是接触长度是很难确定的,文献[1,11-12]中均基于不同的假设提出了斜撑宽度的估计公式。采用的等效斜撑是FEMA-273建议的,斜撑厚度按墙体厚度取值[13]:
w=0.175(λhH)-0.4d
(2)
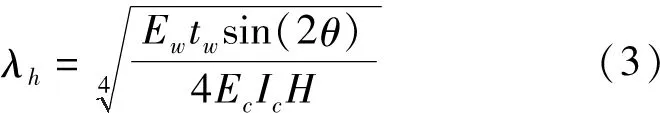
式中:λh为中间参量;Ew为填充墙的弹性模量;tw为填充墙的厚度;Ec为框架柱的弹性模量;Ic为框架柱的惯性矩;H为框架柱高度;d为对角线长度;θ为填充墙对角线与底框架梁之间的夹角。
文献[14]还利用材料力学的方法,计算了该模型的初始等效刚度K:
(4)
对于多遇地震、设防地震的情况,墙体未开裂,依据有限元分析结果,非整墙加固的填充墙Mises应力分布还是沿对角线方向,故等效斜撑模型依然适用。可以注意到,式(4)中刚度与弹性模量呈线性的关系,故在建模时,将不同墙体的弹性模量Ew修正为ηkiEw便可以得到墙体加固后的模型。其中ηki为不同砂浆加固方式对应的刚度增强系数,按非整墙加固有限元模拟结果进行取值。对于罕遇地震的情况,填充墙往往已经开裂。依据非整墙加固有限元模拟结果:高宽比小于等于1.5的墙体产生对角线方向的裂缝,由于该裂缝沿斜撑方向且以受压为主,故认为依然可使用等效斜撑模型;高宽比大于1.5的墙体中部产生了垂直裂缝(图1a),以受剪为主,故建议将墙按中线分为左右两面墙,等效为两根从角部连接至对边中点的双斜撑模型(图1b)。对于这种斜撑模式,按照图1c考虑变形模式,可以计算得到对应的侧向刚度K′:
K′=0.35(λhH)-0.4Ewtwcos2θ′
(5)
现在比较K与K′的大小,将式(4)与式(5)相除,并代入夹角的关系tanθ′=2tanθ得到式(6):

图1 开裂后高宽比较大填充墙双斜撑模拟Fig.1 Double-strut model considering the cracking of higher infilled walls
依据式(6)容易得到,若要K≥K′,则须满足θ≥35.3°,而对于高宽比较大的墙体,此条显然满足。因此,对于高宽比较大,罕遇地震工况下的填充墙,这种建模方式的刚度小于传统等效斜撑模型的刚度,是一种符合实际情况的保守估计。而墙体加固后的模型依然可以依据非整墙加固有限元模拟的结果,通过将墙体的弹性模量Ew修正为ηkiEw得到。
2 填充墙加固前后桥头堡的抗震性能
依据上述模型,利用SAP2000建立桥头堡加固前后在多遇地震、设防地震及罕遇地震工况下的分析模型,并进行结构动力特性和时程响应的对比研究。
2.1 填充墙加固前结构抗震性能分析
采用SAP2000有限元软件对其进行动力特性分析,以了解其抗震性能。依据上文提出的计算方法,分别建立应用于多遇地震工况、设防地震工况分析(图2a)及用于罕遇地震工况分析(图2b)的桥头堡有限元计算模型。依据现场勘查统计和非整墙加固有限元模拟结果,认为高宽比大于1.5的墙体在罕遇地震工况下,须按双斜撑模型进行模拟。有限元模型中的材料参数取值如下(仅考虑弹性):混凝土按实际回弹测试的最小值C15保守估计,重度取23.2 kN/m3,弹性模量取22 000 N/mm2;楼面活荷载取3.5 kN/m2,楼面恒载取5 kN/m2;一层填充墙按实心墙考虑,Ew0取值为2 704 MPa[15],重度取18 kN/m3[16],其余层按空斗砖墙考虑,Ew取值为1 190 MPa[17],重度取12 kN/m3[16];墙厚一层tw0取值为240 mm,其余层tw取值为200 mm;Ec取值为2.2×104MPa。框架柱柱底的边界条件按固接考虑,而斜撑底部则认为是铰接。建立的有限元模型及分析时定义的X、Y向见图2。
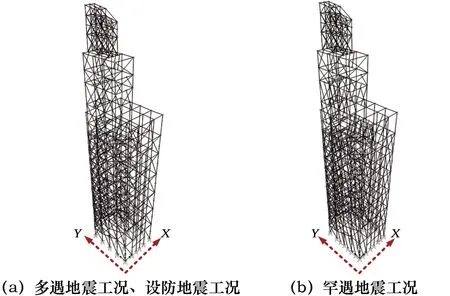
图2 桥头堡有限元模型Fig.2 FEM models of the bridgehead
先对结构动力特性进行了分析,主要考察前三阶固有频率及振型。由于多遇地震工况、设防地震工况与罕遇地震工况采用的是2种斜撑模拟方式,故其自振周期有所区分。2种有限元模型的前三阶固有频率及质量参与系数计算结果见表1。
从表1中的结果可以看出,采用双斜撑模型模拟开裂的填充墙,确实能使结构的刚度有所降低,这与上文理论模型的结果一致:用于罕遇地震工况的模型前三阶固有频率相较用于多遇、设防地震工况的模型有所降低,降低程度约为3%,而且对后两阶的影响稍大一些。另外,从质量参与系数可以看出,2个模型前三阶振型的计算结果亦有差异,多遇、设防地震工况下为第一阶X向平动、第二阶Y向平动、第三阶扭转,但固有频率十分接近,而罕遇地震工况下振型则变为第一阶X向平动、第二阶扭转、第三阶Y向平动。这说明在罕遇地震时,填充墙开裂会导致扭转振型对应的固有频率下降,使结构更容易发生扭转振动,这对结构是不利的。
接着,对桥头堡结构进行了地震时程响应分析。依据相关规范[18],南京地区的设计基本地震加速度为0.10g,设计地震分组为第一组,抗震设防烈度为7度。模型的时程分析按照规范要求考虑多遇地震、设防地震和罕遇地震作用,输入加速度峰值为35 cm/s2、100 cm/s2、220 cm/s2的地震波样本。选取了2条地震波样本,并按比例放大至其峰值达到规范加速度,输入模型进行对比分析。其中1条采用桥头堡在1974年4月22日江苏溧阳发生的5.5级地震中的响应时程,此次地震震中离大桥桥址约85 km,震源深度约15 km,震中烈度7度强。文献[19]给出了这次地震的响应时程,选取桥头堡底层地面测点的响应时程作为激励Sample波,输入模型进行分析;对于另1条加速度时程,选取El-Centro波进行模拟。图3显示了两种激励的时程曲线。
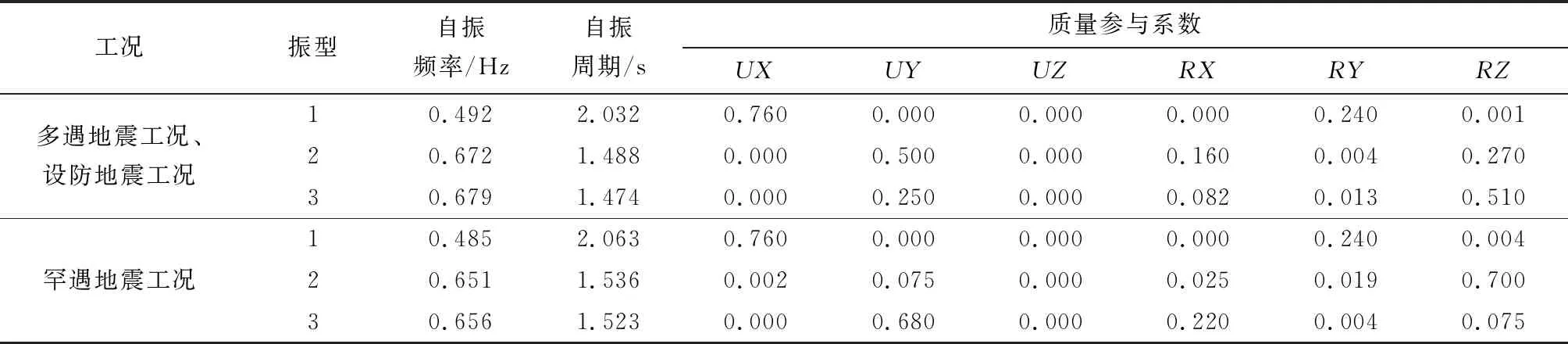
表1 加固前2种有限元模型前三阶固有频率及质量参与系数Table 1 Natural vibration frequencies and participation mass ratios of the two computing models before the infilled walls were strengthened
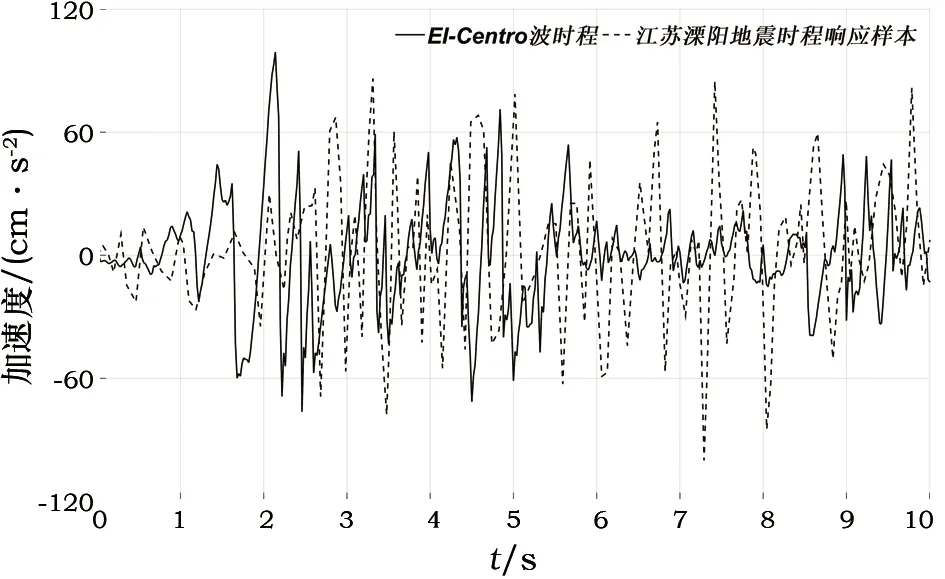
图3 两种激励地震波时程图Fig.3 Time history of two earthquake waves
本次时程分析主要考察2个方向、2种激励下,结构的侧向位移的响应与层间位移角的响应。分析时,选取大堡铁路桥面处、公路桥面处及顶层各1个角点作为研究对象。各工况下公路桥面处(4F)、铁路桥面处(7F)及顶层(10F)X、Y向位移时程结果见图4。El-Centro波激励的位移响应与实际Sample波激励的响应差异大多在10%左右;结构在X向的响应总是大于Y向的位移响应,约为1.6~1.8倍,El-Centro波激励的位移响应峰值在2个方向上的结果差异更大些;不同位置的位移响应峰值随着高度的上升而逐渐递增,公路桥面的位移响应峰值约比铁路桥面增大61%~108%,而顶层的位移响应峰值约比铁路桥面增大121%~174%。
然而,抗震规范[18]中对于各层的位移响应峰值并没有限值,而是限制了层间位移角的大小。故接着将选取各层的角点位移响应,计算各层层间位移角时程曲线,并与规范的限值进行比对。对于一般的钢筋混凝土结构,规范给出的层间位移角限值[θe]为[13]:
[θe]=1/550
(7)
图5为计算所得到的各工况下各层X、Y向的层间位移角响应及其最大值、最小值包络曲线。结构层间位移角在不同幅值的激励下2个方向上的位移响应峰值及出现的位置统计见表2。结果显示,2种激励的层间位移角峰值计算结果差异约为3%~21%,其中:Y向计算结果差异较大;X向的最大层间位移角出现在二层,Y向的最大层间位移角响应出现在八层;结构在2个方向上的层间位移角响应结果略有差别,X向结果大多大于Y向,约是其1.1~1.3倍,但是罕遇地震工况下El-Centro波的Y向响应峰值较X向小,这与实际地震波的计算结果有一定出入;与规范给出的层间位移角限值相比发现,多遇地震情况下的层间位移角响应在2个方向上均满足规范要求,且有较大的冗余,而在设防地震情况下,X、Y向的结果均超过了规范限值,罕遇地震情况下,则2个方向结果均不满足规范要求。

图4 加固前桥头堡公路、铁路桥面层及顶层位移响应时程Fig.4 Displacement responses at highway bridge deck, railway deck and top floor before the infilled walls were strengthened

图5 加固前桥头堡各层层间位移角响应时程及其包络曲线Fig.5 Inter-story displacement angle responses at each floor and its envelope curve before the infilled walls were strengthened

表2 加固前桥头堡各层层间位移角响应峰值表Table 2 Peak value of inter-story displacement angle before the infilled walls were strengthened
2.2 填充墙加固后结构抗震性能分析
为了模拟填充墙加固后对结构抗震性能的影响,依据上文的修正方法,对模型填充墙材料的弹性模量进行修正,以获得桥头堡填充墙加固后的有限元模型。其中,刚度增强系数按非整墙加固有限元模拟结果取值:对于高宽比大于1.5的墙体刚度增强系数取1.935,其余墙体刚度增强系数取1.891。接着,便对加固后的桥头堡模型进行动力特性模拟和时程结果分析。建模所采用的材料参数、分析点的选取、输入的激励时程以及考虑的工况均与2.1节相同。
2种有限元模型加固后的前三阶固有频率及质量参与系数计算结果见表3。

表3 加固后2种有限元模型前三阶固有频率及质量参与系数Table 3 Natural vibration frequencies and the participation mass ratios of the two computing models after the infilled walls were strengthened
对比加固前的固有频率计算结果可以看出,2种有限元分析模型的固有频率在加固后均有提升,提升幅度约在4%~9%。这说明结构在2个方向上的刚度及扭转刚度均有提升。另外值得注意的是,2个模型前三阶振型相较加固前产生了变化,2种模型的振型均为第一阶X向平动、第二阶Y向平动、第三阶扭转,而且扭转振型与平动振型的固有频率差异明显。这说明对填充墙的加固可以明显降低结构在地震工况下发生扭转变形的概率,以减小地震对结构的不利影响。
加固后的公路桥面处(7层)、铁路桥面处(4层)及顶层(10层)X、Y向位移时程响应结果见图6。结果显示:2种激励的位移响应差异与加固前相差不大,但有所增加,约在6%~15%;结构在X向的响应依然大于Y向的位移响应,而位移响应的峰值依然随着高度的增加而递增,这均与加固前类似;但是,值得注意的是,加固后的位移峰值均比加固前有所降低,不同位置、不同方向的位移峰值降低程度有所不同,基本在8%~23%,其中Y向的降低程度较大。此外,相较于加固前,一些工况位移峰值出现的时间也发生了变化。
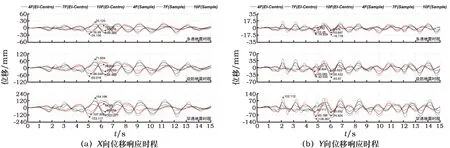
图6 加固后桥头堡公路、铁路桥面层及顶层位移响应时程Fig.6 Displacement responses at highway bridge deck, railway deck and top floor after the infilled walls were strengthened
类似地,依据规范考察加固后桥头堡各层层间位移响应的结果。多遇地震、设防地震及罕遇地震情况下,各层X、Y向的层间位移角响应及其最大值、最小值包络曲线见图7,其各工况下层间位移角的响应峰值及出现的位置统计见表4。结果显示:相较于加固前,加固后桥头堡的层间位移角响应峰值也有明显的降低,降低幅度约在12%~22%,其中Y向的降低幅度较大,另外响应峰值出现的位置也出现了一些变化;结构在X向的层间位移角响应大多大于Y向,而罕遇地震工况下El-Centro波的Y向响应峰值较X向小,与实际地震波结果依然存在出入,这些结论与加固前类似;与规范给出的层间位移角限值相比发现,多遇地震情况下,在2个方向上层间位移角响应进一步减小,均满足规范要求;在设防地震情况下,2个方向的响应峰值均下降至规范要求以内,满足要求;而罕遇地震情况下2个方向结果虽然不满足规范要求,但均有一定程度的下降。

图7 加固后桥头堡各层层间位移角响应时程及其包络曲线Fig.7 Inter-story displacement angle responses at each floor and its envelope curve after the infilled walls were strengthened

表4 加固后桥头堡各层层间位移角响应峰值表Table 4 Peak value of inter-story displacement angle after the infilled walls were strengthened
3 结 论
研究南京长江大桥桥头堡填充墙加固后对结构抗震性能的影响,提出考虑高填充墙开裂后结构效应的双斜撑模型,可用于罕遇地震工况下的结构抗震性能计算,接着又提出考虑填充墙加固后刚度增强效应的建模方法。最后建立桥头堡加固前后用于多遇地震工况、设防地震工况及罕遇地震工况的分析模型,进行了桥头堡的抗震性能对比。
1) 桥头堡填充墙加固后结构的动力响应均明显下降,位移响应峰值下降约8%~23%,层间位移角响应峰值约下降12%~22%,Y向下降更为明显,这是由于Y向填充墙较多造成的。填充墙加固后,结构在设防地震工况下2个方向的层间位移角均满足了规范要求。这说明,填充墙加固后桥头堡抗震性能有了明显提升。
2) 引入双斜撑模型后,罕遇地震工况下模型前三阶固有频率约下降3%,扭转振型从第三阶降至第二阶。这说明罕遇地震工况下填充墙的开裂有可能会使结构的扭转刚度下降,使结构更易发生扭转变形。
3) 桥头堡填充墙加固后结构的前三阶固有频率约提升4%~9%,且2种模型的扭转振型均上升至第三阶。这说明填充墙加固会提升结构的扭转刚度,可以有效避免墙体开裂带来的不利影响。
4) 2种地震波激励的时程响应结果存在一定差异:位移、层间位移角峰值的计算结果差异在3%~21%,而且2种激励下峰值出现的时间点、位置等也存在不一致的情况。故进行时程分析时建议综合考虑不同的地震波进行分析。
