额外维和宇宙氦丰度的相关性质研究

黎聪笑， 颜 骏， 赵 峰

（四川师范大学 物理与电子工程学院，四川 成都610066）

在宇宙学标准模型中，宇宙的演化过程大致可分为4 个时代［1-4］.

（I）强子时代：温度介于T=1031～1012K.在这一时代中宇宙的物质是高度相对论性的基本粒子以及反粒子构成的等离子体.这些粒子包括夸克、胶子、电子、μ子、τ 子、中微子、光子、W和Z 玻色子、引力子及其反粒子.强子时代中粒子的总自旋状态数g*≈106.75，起止时间为t=10-43～10-4s.

（II）轻子时代：温度介于T=1012～4 ×109K.在这一时代只有较少量的粒子存留下来.残留的粒子包括光子、引力子、质子、中子、电子、μ 子、τ 子、中微子及其反粒子、引力子及其反粒子.轻子时代中粒子的总自旋状态数g*≈21.25，起止时间为t=10-4～10 s.

（III）辐射时代：温度介于T=4 ×109～104K.在这一时代，电子将产生湮灭效应，残余电子的密度与质子和中子的密度均远小于光子和中微子的密度.辐射时代中粒子的总自旋状态数g*≈7.25，起止时间为t=10 ～1012s.

（IV）物质时代：温度T＜104K.这一时代开始时，辐射密度将低于物质密度，电子与质子结合形成中性氢原子和氦原子，物质与辐射之间的耦合作用将变得很弱，物质时代的起止时间为t=1012s ～137 a.

上述宇宙演化过程中的起止时间都是由Einstein宇宙学场方程和量子统计物理原理结合而估算出的.目前天文学观察表明宇宙中最普遍的化学元素是氢元素，丰度为75%，而4He 丰度约25%，其他的轻元素或金属所占有的丰度很小.由于大量的4He不可能在星体内部出现，所以对氦丰度比较合理的物理解释是4He 产生于宇宙早期的热运动之中.这时氦产生的数量与中子的利用率有关，而弱相互作用保持了中子和质子之间的化学平衡.当温度降至几MeV 以下时，这些弱相互作用将会失效.因此，质子与中子的比率将被“冻结”，所以原初的核合成完成于大爆炸后的几分钟，对应辐射时代的早期阶段，这时自由质子和中子将结合成氦元素和其他元素.目前，氦丰度的理论计算和观测数据较为一致，这是对宇宙学标准模型的一个有力支持，美国宇宙学家Peebles 由于微波背景辐射理论和氦丰度计算的早期工作获得2019 年度诺贝尔物理学奖.

在额外维空间随时间演化的宇宙模型中［5］，3维空间中的基本耦合常数也可能随时间发生变化.这些耦合常数包括精细耦合常数α、弱作用耦合常数GW、强作用耦合常数αs、引力耦合常数G.它们与额外维空间的标度因子（或半径）R及额外维内部空间的维数d有关.Kolb等［6］首先研究了3 种基本耦合常数α、GW、G 随时间变化时对大爆炸核合成的影响，当氦丰度的观测值取为Yp=0.24 ±0.01时，那么D=10 的超弦模型［7］给出的内部空间尺度变化约为0.5%，D=6 和D=11 时的Kaluza -Klein模型［8-12］给出的内部空间尺度变化约为1%.随后Barrow［13］进一步考虑了强作用耦合常数αs随时间变化时的原初核合成过程，当氦丰度的观测值取为Yp=0.24 ±0.01 时，计算结果表明10维超弦模型给出的内部空间尺度变化小于0.2%，而6 维和11 维的Kaluza-Klein模型给出的内部空间尺度变化小于0.7%和1.1%.因此，Barrow［13］进一步改进了Kolb 等［6］的计算结果.文献［14 -30］分别研究了量子修正和有限温度修正下反应率对原初核合成的影响，还讨论了氦丰度对引力耦合常数和额外维模型中物理参量的约束.

本文考虑3 种耦合常数α、GW、G 随时间发生变化的情况，在Mukhanov 给出的核合成反应率公式［13-14］的基础上重新计算了额外维数d对氦丰度的影响.首先，当额外维半径变化值取ε =10-2和ε=10-3时，分别计算了d=2 到d=11 时的氦丰度数值，结果发现ε =10-2时，额外维数的变化对氦丰度的变化有较明显的影响；而当ε =10-3时，额外维数的变化对氦丰度变化的影响很小.其次，本文考虑了额外维半径R随时间振荡变化的情况，分别计算了δ=10-2和δ=10-3时额外维数d和约化振荡周期同时增加时的氦丰度变化值，结果表明δ=10-2时，氦丰度的变化比较明显，而δ=10-3时，氦丰度的变化值很小.本文还将讨论和分析额外维效应和振荡效应存在时的氦丰度变化规律.

1 早期宇宙中的氦丰度计算结果

宇宙学标准模型中的Friedman方程为

其中，H是Hubble参量，ρ为物质密度，由于极端相对论气体在宇宙早期的物质分布中占主导地位，此时物态参量为γ=1/3，所以有

在电子和中微子作用下，宇宙早期的中子-质子有3 种相互转化的反应式

随着宇宙的膨胀，宇宙的温度开始下降，当宇宙的膨胀速率等于反应率时H=T，那么此时的温度被称为冻结温度Tf，也称为退耦温度.在非相对论极限下的中子-质子数密度之比为

其中Q是中子和质子的质量差.另外，4 费米子相互作用a+b→c+d的微分截面可用下式［3］给出

其中矩阵元为

|M|2=费米耦合常数取为GF≈1.166 37 ×10-11MeV-2，gA≈1.273 9为轴矢量耦合常数，（Pa·Pb）和（Pc·Pd）为4 -动量的标积，ma，b，c，d为反应粒子的质量.首先考虑温度在几个MeV 下的反应n +νe⇆p +e-，其中核子是非相对论的，这时有如下近似：

其中，mp、mn和me分别表示质子、中子和电子的质量，ve是电子的速度，εν是入射中微子的能量，εe≈εν+Q是出射电子的能量，将（6）-（7）式代入（5）式得到的微分截面为

其中忽略了中微子的mν的质量，对（8）式积分后可得到的反应率为

当温度kT＞2mec2时，电子的能态被电子-正电子对所占据，根据Pauli不相容原理，这时微分截面减少为

这时在时间间隔Δt内给定体积内的中子数Nn的减少量为

其中（nεν=1/1 +eεν/kT）表示中微子所占据的数目，vν和Tν分别表示中微子的速度与温度，并且

为相体积元，而中子丰度定义为

这里假设早期宇宙中的重子数守恒，于是nν-过程中的中子丰度的变化率为

其中Γnν表示衰减率.又由方程（10）和（11）可得

其中，Γ（Tν）表示衰减率Γnν中的积分函数，是当温度低于kT≈2mec2时，由于Pauli不相容原理，其中（1 +e-εe/kT）项的贡献可以设为1，又因为mec2/εe≪1，对剩下的部份引入积分变量x=εν/kTν有

所以反应率最终表达式为

其中，βν=1/kTν，常数ζ（5）=1.037 44，并且有数值关系（45ζ（5）/2）/（7π4/30）= 1.027，又称为Mukhanov反应率［13-14］.如果仅考虑如下两体反应

那么反应率约为2Γσν.当H=2Γσν时热平衡处于临界状态，由此可导出退耦温度满足的方程为

（20）式可以进一步化简为

其中，中子和质子质量差Q=1.293 MeV，轴矢量耦合常数gA≈1.273 9，费米耦合常数GF≈1.166 37 ×10-11MeV-2，引力耦合常数G = 6.703 × 10-39GeV-2，ζ（5）=1.037 44.当宇宙处于退耦温度时，其中仅存在正负电子、光子和3 种正反中微子，并且mp/mn可近似取为1.这时粒子的总自旋态数为

将上述质量差、耦合常数和总自旋态数代入（21）式中有

数值计算后得到的退耦温度Tf≈0.704 085 MeV.接下来可计算氘合成的开始时刻tD，由质子和中子形成氘和光子的反应为

同理，可根据Friedman方程（2）来计算氘合成的开始时刻，这时

此时的早期宇宙仍以辐射为主，物态参量为γ =1/3，于是有

此时光子的温度可视为宇宙的温度，随着宇宙温度的下降，中微子等离子体与宇宙流通光子之间不再保持充分的热接触，这些中微子的温度与宇宙温度不再一致.所以，粒子的有效总自旋状态数将变为如下更一般的形式

这时中微子和光子温度关系为

正负电子湮灭后的g*为

此时正负电子对g*无贡献，中微子有3 种，即Nν=3，所以g*变为

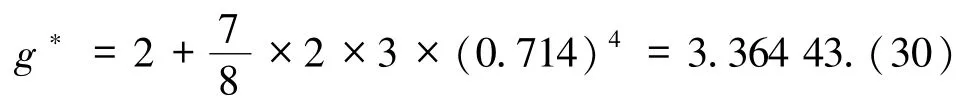
由核物理中给出的氘合成温度为TD=0.086 MeV，将其代入（26）式可得到氘合成的时间为

由于中子可进一步发生放射性衰变，并且遵守如下衰变关系

其中N0为t=0 时的粒子数，N为经过时间t后还留存的粒子数，λ 为衰变常数，这时中子平均寿命为

将（33）式代入（32）式中有

因此考虑了中子自发衰变效应后的中子-质子比变为

其中取中子平均寿命取为TD=885.7 s，代入退耦温度，氘合成的时刻及中子平均寿命后，那么通过计算得到的中子-质子比值为

又因为4He核是由2 个中子和2 个质子构成，而宇宙中的所有中子和部分质子将构成氦核，设mHe为单个4He的质量，nHe为其数密度，核子质量mN≈mn≈mp，那么氦丰度YP定义为

4He核中有4 个核子，即mHe≈4mN，4He 核中有2个中子，假定宇宙中所有的中子最终都合成进入了4He核，即nHe=nn/2，那么（37）式变为

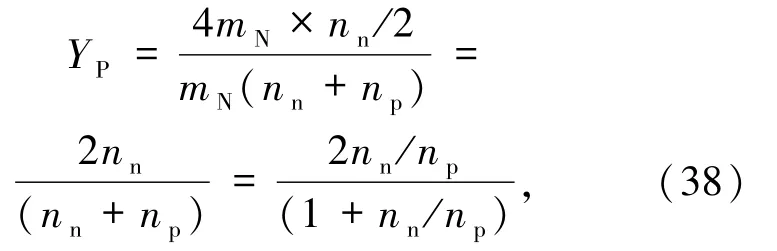
又由（38）式可计算出此时的氦丰度YP约为

这与当前氦丰度的观测值取YP=0.24 ±0.01.

2 额外维空间存在时的氦丰度修正值

首先观察未考虑额外维空间存在时的平衡方程（20）式，其中3 种耦合常数α、GW、G 将影响退耦温度的数值.当存在额外维空间时，或称为K-K效应产生影响时，那么这3 种耦合常数随额外维空间的标度因子（或半径）R及维数d的变化关系分别为

其中，α=e2为精细结构常数，Δm∝α 表示中子和质子的质量差正比于精细结构常数.b0表示当前的额外维半径，b（t）表示氦合成时的额外维半径，GF0表示氦合成时的弱耦合常数，GF（t）表示当前的弱耦合常数，α0表示氦合成时的精细结构常数，α（t）表示当前的精细结构常数，G0表示氦合成时的引力耦合常数，G（t）表示当前的引力耦合常数，额外维半径变化值可设为b（t）/b0=1 +ε ＞1.所以，有如下关系：

当额外维半径变化值分别取ε =10-2和ε =10-3时，通过数值计算可得氦丰度修正值，如表1所示.

表1 当ε=10-2，退耦温度、中子数-质子数之比及氦丰度与额外维的关系Tab. 1 The relationship between decoupled temperature，the ratio of neutron number to proton number and helium abundance with the extra dimensions when ε=10 -2

3 额外维空间振荡变化时的氦丰度修正值

K-K效应存在时的一般形式下的退耦温度方程为

其中，（1 +ε）=b（t）/b0＞1，b（t）为氦合成时的额外维紧致球半径，b0为当前的额外维空间半径.如果标度因子随时间发生周期性的振荡变化，那么可做如下假设

其中，ω=2π/T*为振荡频率，T*表示振荡周期，当t=t0时，可给出如下初值条件b（t0）=b0（1 +δsin ωt），即当前的额外维为周期性振荡的起点，那么有sin 2π·t0/T*=0，其中t0表示当前的宇宙年龄，所以有如下关系

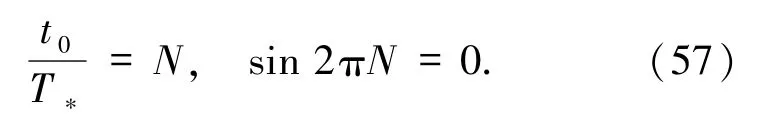
其中，N为额外维半径的振荡次数，当前的宇宙年龄为t0=4.352 ×1018s，所以振荡周期为T*=t0/N=4.352 ×1018/Ns.进一步，设N=1018/n，将N带入T*中即可得关系式T*=4.352ns，这里n的物理意义可以理解为额外维半径的约化振荡周期，其变化值如表2 所示.

表2 额外维半径约化振荡周期n和振荡周期T*的变化值Tab. 2 The variation values of reduction oscillation period and oscillation period for extra dimension radius

这时，sin 2πtD/T*= sin 2πN·tD/t0，又因为N=1018/n，并且tD=178.604 s，所以有

由此得到具有振荡效应时的修正退耦温度方程为

其中，δ =10-2，10-3，Tf的单位是MeV，通过数值计算得到额外维数d与约化周期n改变时氦丰度YP的变化关系，如表3 和4 所示.

表3 δ=10-2时额外维数d与约化振荡周期n和氦丰度YP 关系Tab. 3 The relationship between extra dimensions and reduction oscillation periods with helium abundance when δ=10 -2

表4 δ=10-3时额外维数d与约化振荡周期n和氦丰度YP 关系Tab. 4 The relationship between extra dimensions and reduction oscillation periods with helium abundance when δ=10 -3

4 结论与讨论

本文首先由4 费米子相互作用的散射微分截面导出了Mukhanov 反应率的表达式，然后根据Einstein- Friedman 方程计算出了退耦温度Tf≈0.704 MeV，以及氘合成的时间tD≈178.55 s，最后在此基础上计算出了宇宙氦丰度的数值约为YP=0.231.

当额外维空间存在时，那么精细耦合常数α、弱作用耦合常数GW、引力耦合常数G 的变化将随时间和内部空间尺度R（t）发生变化，并且G 变化与额外维空间的维数有关，其中，弱作用耦合常数GW和引力耦合常数G 的变化将通过宇宙学平衡方程影响退耦温度Tf的数值，引力耦合常数G 的变化将影响氘合成的时间tD；另外，精细耦合常数α的变化将影响质子和中子的质量差.因此，3 种耦合常数随时间和内部空间标度因子的变化将通过质子-中子的粒子数之比［np/nn］的变化体现出来，这些耦合常数随时间变化的综合效应将影响氦丰度的计算数值.

其次，本文还采用了Mukhanov 反应率公式，并根据额外维空间存在时的平衡方程，进一步推导出了退耦温度的Tf的修正表达式.当额外维标度因子的变化值取为ε =10-2，并且额外维空间维数由d=2 至d=11 变化时，那么可以通过数值计算得到关于氦丰度的一系列修正值.结果发现随着d的增加，氦丰度的数值也变大并介于YP=0.217 ～0.226之间.当ε =10-3时，数值计算得出的氦丰度约为YP=0.230，随着d的增加，YP几乎不发生改变.这些研究结果说明了额外维尺度的数量级变化较大时，氦丰度随空间维数的增加而变化较为明显.

另外，本文还计算了当额外维空间随时标度因子间振荡变化时的氦丰度值.当额外维尺度变化的数量级值取为δ =10-2，约化振荡周期介于100≤n≤103之间，维数由d=2 至d=11 变化时，氦丰度值呈平缓增加的趋势；当约化振荡周期n=104时，那么随着维数d的增加，氦丰度值几乎不发生改变.当δ =10-3，并且约化振荡周期介于10 ≤n≤103之间时，计算结果表明随着维数由d=2 增至d=11，氦丰度值YP≈0.230 并且不发生改变；当约化周期介于n=104时，那么随着维数d的增加，YP≈0.231 也不发生改变，但是对应的氦丰度值略大.因此，额外维尺度数量级变化较大时，无论随着空间维数d的增加，还是约化振荡周期的增大，氦丰度数值的变化都较为显著，本文的研究为从宇宙学的角度证实额外维空间是否存在提供了一定的理论依据和观测对比.