基于蒙特卡洛仿真的小麦仓储环节菌落总数风险评估方法

王小艺，陈 谦，赵峙尧,*，熊 科，史 策，裴鹏钢

（1.北京工商大学计算机与信息工程学院，北京 100048；2.北京工商大学，中国轻工业工业互联网与大数据重点实验室，北京 100048；3.北京工商大学，北京市食品添加剂工程技术研究中心，北京 100048；4.北京市农业信息技术研究中心，北京 100097）

小麦是世界第二大粮食作物，也是中国继玉米和大米之后的第三大作物。20世纪80年代初以来，全世界的小麦产量显著增加，中国每年的小麦产量超过1.2亿 t，已成为世界上最大的小麦生产国。然而，近年来小麦食品安全问题层出不穷并引起了社会各界的广泛关注[1-4]。风险评估是一种结构化的科学过程，用于估计风险的概率和严重程度以及随之而来的不确定性，以确定因接触食物中的生物、化学或物理危害物而对健康生活造成的潜在危害和相关风险[5-6]。国际食品安全组织正大力推动将风险评估技术应用于评估食品中危害物安全的问题[7]。目前的中国食品安全法要求建立国家食品安全风险评估制度，以评估中国食品中的危害物风险[8]。

现有的食品安全风险评估方法主要分为两类：定性风险评估方法和定量风险评估方法[9]。定性风险评估是一种基于专家经验的风险评估方法，主要是根据评估专家的经验和知识对风险进行分析判断，并据此来描述评估结果[10]。目前已有的定性风险评估方法包括德尔菲法、决策树、危害分析临界控制点（hazard analysis critical control point，HACCP）等[11]。这些方法多被应用于食品供应链中物流、经济、信息等因素的风险管理优化，通过建立相应的风险指标体系评价食品安全风险水平。定量评估方法是指依据理化实验抽检或数据驱动模型获取相关定量数据，并通过分析计算出风险指标的量化值，以描述食品安全风险水平[10-13]。其中，理化实验抽检方法包括色谱法、聚合酶链式反应法、光学传感器法等[12]；常用的数据驱动方法包括灰色关联度分析、支持向量机、蒙特卡洛仿真等[13-14]。这些方法多用于危害物的风险定量评估。结合已有研究分析[15-16]，定性风险评估方法大多依赖风险评估者的主观经验，受专家自身素质的影响大。然而，由于现代食品安全监控数据具有维度高、随机性强等特性，该类方法难以满足风险评估的精度要求。对于定量风险评估方法，理化实验抽检方法一般对实验设备及实验环境要求较高，实验周期较长，相关学者致力于快速无损检测技术的研究，并取得了一定成效，但单点检测无法满足食品安全预警要求，数据驱动模型的评估预测能力强弱更多取决于数据的准确性高低以及体量大小。同时，已有的食品安全定量风险评估缺少直观明确的度量指标，大多数已有的食品安全风险评估方法都是通过危害物含量直接量化风险，模型演化过程的随机性及环境的不确定性会导致危害物含量的测量精度较低。

考虑到定性和定量风险评估方法各自的优缺点和风险度量指标研究的不足，本实验以小麦仓储环节中菌落总数为评估对象，研究一种针对生物性危害物的风险评估方法。首先，建立可以适应不同生长环境的菌落动态生长模型；在此基础上，通过蒙特卡洛仿真对小麦仓储环节中菌落总数概率分布进行预测；最后，提出风险度量指标“危害度”，并基于该指标对小麦仓储环节中菌落总数风险进行定量评价。该风险评估方法可以为风险管理和决策部门提供实时、直观的风险评估结果，为风险防控提供理论支持。

1 菌落动态生长模型构建

在微生物生长允许的环境条件下，微生物生长绝大部分需经历迟滞期、指数期和稳定期[17-18]。预测微生物学中常使用数学机理模型来描述微生物的动态变化，这些机理模型一般可分为初级模型、二级模型和三级模型[19-22]：初级模型用来描述在恒定环境下，微生物随时间的生长状况，其动力学参数决定了特定微生物在特定恒定环境下的生长特性；二级模型用来模拟环境条件对微生物动力学参数的影响，例如温度和相对湿度对初级模型中生长速率和迟滞期的影响；三级模型是通过多种一级模型与二级模型组合成的系统软件，来描述动态环境下不同微生物的生长状况[23]。本实验中菌落属于一类微生物，其含量用菌落总数表示，可用来评估食品被有害菌落污染的程度及其卫生状况。

对于菌落的动态生长，引入采样时刻k＝{h,2h,…,K}，其中h为采样周期/d，K为采样时长/d，菌落动态生长模型按公式（1）[20-21]计算。

式中：Nk和Nk－h分别为k和k－h时刻的菌落总数/（CFU/g）；f[k－h,k]为在[k－h,k]时间段内菌落生长数量增量/（CFU/g）。

本实验中f[k－h,k]通过菌落生长Logistic初级模型[21]获得，如公式（2）所示。

结合公式（1）、（2），建立菌落动态生长模型，如公式（3）所示。

式中：λk受温度T/℃和湿度αw变化的影响，可通过二阶多项式函数（二级模型）描述[24]，C0～C5为函数参数；μk受温度T和相对湿度αw变化的影响，可通过多因子基数模型（二级模型）描述[25]，τk和ρk分别为多因子基数模型中温度因子和湿度因子，μopt为菌落生长比生长速率最适值；Tmin、Tmax分别为菌落生长温度区间最小值和最大值，Topt和αw,opt分别为菌落生长最适温度和最适相对湿度，αw,min为菌落生长湿度区间最小值，Tk和αw,k分别为k时刻的温度和相对湿度，它们的数值变化可通过环境演化模型fT和fαw描述。

定义菌落动态生长模型的菌落生长指标x根据公式（4）计算。

假设以上模型参数θ为慢变量（近似恒定），公式（3）可简化为公式（6）。

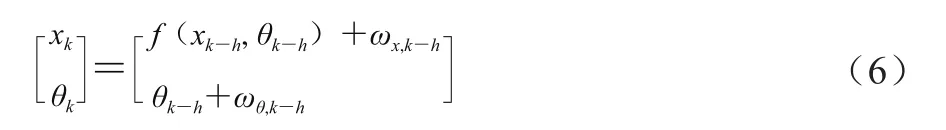
式中：f为菌落动态生长模型函数；ωx、ωθ分别为菌落生长指标和模型参数变化中受到的高斯噪声干扰[26]，分别满足ωx,k∶N（0,Σx）、ωθ,k∶N（0,Σθ），k∈[0,K]，∑x、∑θ为对应的噪声协方差阵。

需要注意的是，不同菌落生长特性不同，同种菌落的生长环境也会有差别，因此，不同菌落动态生长模型参数也不同。为使模型更为精确、合理，模型参数θ的取值需结合实测数据和相关参数估计方法确定。

2 小麦仓储环节中菌落总数的概率分布预测

2.1 蒙特卡洛仿真

蒙特卡洛仿真是以中心极限定理和大数定律为基础的概率统计方法，通过对模型演化进行规律性模拟，以估计参数的不确定性。根据中心极限定理，可以从有限的随机样本群中随机抽取服从特定分布规律的样本，根据大数定律，可以通过统计反复实验过程中某事件发生的频率来近似地获取随机事件的概率[27]。基于以上两点定理，蒙特卡洛仿真通常适用于优化、积分、随机概率分布等数学问题中的解析无法被精确计算的情景[28-29]。

一般的蒙特卡洛仿真过程为：1）确定模型的参数变量及基本特征；2）根据问题和实测数据构造随机模型；3）根据模型中各个随机变量的分布产生随机数并进行多次随机采样；4）通过多次模拟获取实验结果并统计分析获取问题的概率解以及解的精度估计[30]。

2.2 基于蒙特卡洛仿真的小麦仓储环节中菌落总数的概率分布预测

考虑到蒙特卡洛仿真作为定量风险评估方法在处理微生物生长演化过程的随机性及环境不确定性问题上的优势[31]，本实验基于蒙特卡洛仿真对菌落总数概率分布进行预测。

首先，假设小麦仓储环境为恒温恒湿，则公式（3）中菌落动态生长环境演化模型可用公式（7）、（8）表示。

式中：Tset为设置的恒定温度/℃；αw,set为设置的恒定相对湿度；ωT和ωαw分别为环境温度和湿度演化模型的高斯噪声干扰，分别满足ωT,∶kN（0,QT）、ωαw∶,k N（0,Qαw），k∈[0,K]，QT、Qαw为对应的噪声协方差阵。

基于以上设置，可利用蒙特卡洛仿真对菌落总数演化过程进行模拟。针对蒙特卡洛仿真中的每一次模拟，同一指标在同一预测时间点的数值均不相同，这些数值同时具有规律性和随机性。规律性体现在预测值是基于确定的菌落动态生长模型、确定的菌落生长指标和模型参数初值产生的；随机性体现在每一个菌落生长指标在每一个预测时间点均受噪声影响，导致得到的预测值不尽相同。当模拟次数足够大时，结合概率统计规律，可以获得各菌落生长指标在不同时间点上取值的概率分布。基于蒙特卡洛仿真的小麦仓储环节中菌落总数概率分布预测的具体步骤为：

1）设置菌落生长指标初值x0，模型参数初值θ0，蒙特卡洛仿真所用粒子数D/个；

2）对第d∈[1,D]个粒子，在k＝0时刻，按照公式（9）赋予初值；

3）对于时刻k∈[0,K]，基于k－h时刻的菌落生长指标和模型参数，根据公式（6）进行单步预测，分别得到；

4）若k≤K，k←k＋h，返回步骤3，否则进行步骤5；

5）若d≤D，d←d＋1，返回步骤2，否则进行步骤6；

6）对k∈[0,K]，按照公式（10）计算菌落总数的概率密度函数P（xk|（x0,θ0））；

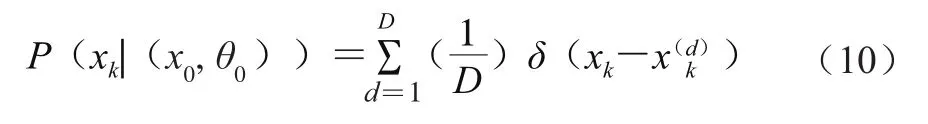
式中：P（xk|（x0,θ0））为基于初始值（x0,θ0）的条件概率密度函数；δ（·）表示狄拉克函数。

大数据已经发展成社会和时代发展的主要属性，伴随国家“互联网+”策略的落实，在全新的阶段，需要将大数据置于重点位置，这也是必然的变革趋势[1]。刘延东副总理在首届国际教育信息化大会上明确强调了“互联网+”战略的重要地位，给出的倡议为:需要更加注重教育领域的信息化发展，利用创新技术来推动教学工作的发展，确保受教育者能够公平地享用信息技术，并为不同文明的交流提供有利条件。

3 基于“危害度”的小麦仓储环节中菌落总数风险评估

在系统工程领域，相关学者基于可靠性理论中性能可靠度的定义和安全性分析中安全概率的定义[32-33]，提出了“健康度”的概念，并以此作为评估系统工作性能及表现的度量指标[34-35]。本实验参考“健康度”的思想提出了新的度量指标“危害度”，并基于该指标对小麦仓储环节中菌落总数风险进行定量评价。

对于一般动态系统，其风险指标所在的n维空间Rn可划分成一个无风险空间SH和一个有风险空间SF（SHUSF＝Rn）。对于某一时刻k，系统的危害度Rk可按公式（11）计算。

式中：Rk为k时刻该动态系统处于有风险状态的概率，也称危害度；对于小麦仓储环节的菌落总数而言，小麦仓储环节中菌落生长指标x的演化过程可以看成一个动态系统。

结合公式（10），小麦仓储环节中菌落总数“危害度”可通过公式（12）计算。

式中：SF＝{xk|Nk＞Θ,Nk∈xk}，Θ为菌落总数超标阈值/（CFU/g）；Rc,k∈[0,1]，Rc,k＝0表示k时刻小麦仓储环节中菌落总数无超标风险；Rc,k＝1表示k时刻小麦仓储环节中菌落总数存在超标风险。

4 案例验证

以定量菌落总数为例，基于MATLAB软件并通过实测数据演化曲线对比来验证小麦仓储环节中菌落总数概率分布预测及风险评估方法的有效性。其中，实测数据演化曲线来源于文献[36]，其研究对象为小麦在储藏过程中的霉菌活动特性，包括以蠕孢霉和链格孢霉为主的混合霉菌菌落总数演化特性。

4.1 实验参数设置

如表1所示，设置菌落总数生长模型实验参数。

表1 参数设置Table 1 Parameter settings

4.2 结果与分析

图1为混合霉菌动态生长模型中比生长速率μ和生长迟滞期λ的温度-相对湿度响应曲面图。由图1A可知，μ随温度和相对湿度的增大呈先增大后减小的趋势，在最适温度和相对湿度时，μ最大；由图1B可知，λ随相对湿度增大而减小；随温度升高呈先减小后稍微增大的趋势，在最适温度附近时λ最小。这两个菌落生长二级模型的响应曲面图符合菌落生长特性，进一步证明了菌落动态生长模型的有效性。

图1 比生长速率（A）与生长迟滞期（B）的温度-相对湿度响应曲面图Fig.1 Temperature-humidity response surface plots of specific growth rate (A) and growth lag (B)

根据2.2节中基于蒙特卡洛仿真的小麦仓储环节菌落总数演化算法对其进行概率分布预测，结果见图2。为更直观地表现菌落总数的分布特征，通过蒙特卡洛仿真中大量重复实验的粒子群统计并计算特定时刻的菌落总数概率分布函数（图3）。

随着时间的延长，菌落总数的生长演化规律呈现发散状态，这是由于小麦仓储环节中菌落的生长受到演化过程的随机性和环境不确定性的影响。并且随着时间的延长，菌落总数的演化曲线整体呈现先平坦后陡增的趋势，这说明菌落生长是一个从慢变到爆发的过程，这符合菌落在生长迟滞期和指数期的生长特性（图2）。菌落总数的概率函数随时间的延长呈现由高窄向矮宽的变化过程，体现出菌落生长的随机性随时间延长而增加的特点，曲线越高则表示菌落总数出现概率越大（图3）。结合图2、3可知，菌落生长趋势符合菌落生长规律并稳定在一定范围内，其具有确定性；同时，小麦的仓储环境虽然稳定，但是由于环境不确定性的影响，菌落总数概率分布预测具有一定的随机性。

本实验通过25 ℃、相对湿度0.6条件下‘郑麦004’在仓储环节中霉菌菌落总数的35 d实测数据演化曲线（数据间隔为7 d）验证模型的有效性。实测数据演化曲线为图2、3中的深蓝色曲线，该曲线符合菌落生长规律，并基本被相同环境条件下的菌落总数蒙特卡洛仿真演化曲线覆盖，这说明了该模型的有效性。各时刻菌落总数的实测数据接近蒙特卡洛仿真中相同时刻出现概率较高的菌落总数数值，这进一步验证了模型的有效性。

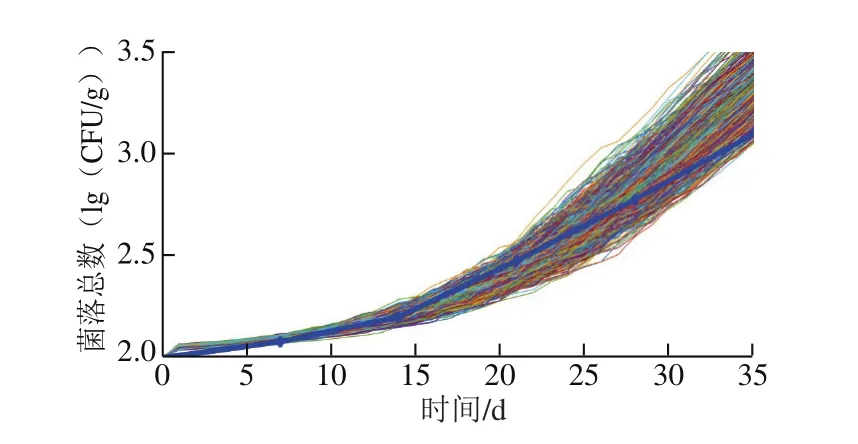
图2 基于蒙特卡洛仿真的菌落总数演化曲线Fig.2 Evolution curves of total bacterial count based on Monte Carlo simulation

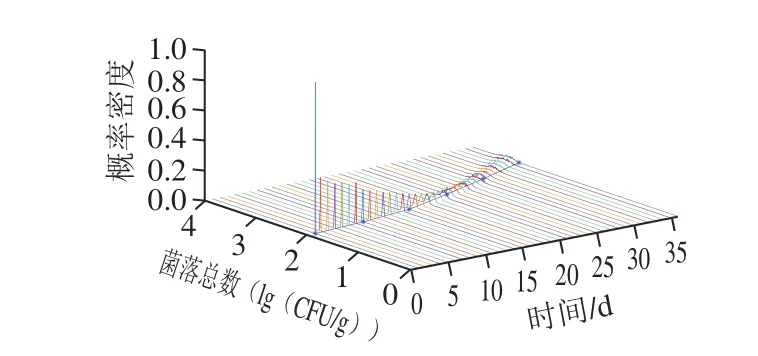
图3 菌落总数的概率分布函数Fig.3 Probability distribution function of total bacterial count

在不同时间菌落总数的概率分布结果的基础上，计算不同时刻菌落总数的危害度，定量评价菌落总数风险的变化趋势，结果见图4。结果表明，危害度呈现先平坦后陡增、并逐渐趋近于1的趋势。其符合菌落生长规律，能够直观明确地对菌落总数风险进行量化评价。

图4 时区[15,30]下小麦仓储环节中菌落总数危害度变化曲线Fig.4 Variation in the hazard degree of total bacterial count during wheat storage

5 结 论

本实验考虑了蒙特卡洛仿真在微生物风险评估中的优势，弥补了模型演化过程的随机性及环境的不确定性对风险定量评估的不利影响，并结合度量指标“危害度”进行风险定量评价，降低风险评估的偶然性、提高其准确度和直观性。未来研究主要分为两个部分：1）本实验研究的是单一环节中危害物的风险演化过程，而食品供应链是一个面向市场的组织网络，针对其复杂的环节切换及环境变化，需进一步研究完整供应链上危害物的风险评估方法；2）基于蒙特卡洛仿真的风险评估方法需建立一定规模的粒子群，并对每个粒子进行完整的演化模拟实验，这必将增大模型计算复杂度从而导致运算效率较低，针对这一缺点，需进一步从数学计算机理出发，通过改进数学解析算法降低风险评估方法的计算量，以提高其评估速度。