多尺度空间面群目标相似性度量方法研究

陈 杰，韩 亮，梁 洁

(山西大同大学建筑与测绘工程学院，山西大同 037003)

相似性度量研究是空间数据更新、检索查询、聚类和异常检测等方法的基础，同时也是从深入探索地理实体或地理现象形成、演化和异质性规律的关键之一[1-2]。相似度计算时涉及因素很多，需拓扑、方向、序数、语义、距离、大小和形状关系描述的支撑[3-6]。面群目标是地理空间分布的重要实体。以济南市部分区域建筑面群专题及其制图综合后专题图为实验对象，从距离、方向、形状、大小四方面进行相似性度量，给出相应测度模型。

1 相似度的计算

1.1 距离相似度

距离是描述空间目标相对位置关系、反映目标邻近程度的一种空间约束，在邻近分析、聚类分析、图像匹配以及目标跟踪等诸多空间分析与处理领域有着广泛应用。因此，分析目标间几何特性时,距离测度较为关键。距离相似度意味着每个目标相对于其他目标而言，可以用一个距离差异值来表示。对于面群目标来说，该差异值能准确地反映空间面群目标综合前后相对位置变化。较多文献对距离度量方法，如最近距离、最远距离、质心距离、曼哈顿距离等均有介绍，然而，大多数研究在距离测度时，难以表达空间目标间距离的分布规律。基于此，邓敏等人从计量统计学角度，提出了一种广义豪斯道夫距离度量模型[7]，能够定量测度目标间距离分布趋势，可将该方法进行改用于度量面群目标距离相似性。

设O为参考目标（单个点目标），A集合为群目标，令

式中：⊕为膨胀算子；0 ≤τ≤1；θ(·)为一个度量函数，取值为0或者交集面积；C(r)表示半径为r的一个闭球。

定义：

式中：Dis(O,A)为O,A的距离度量。

由式（2）可知，Dis为闭球C的半径，以至于集合A包含在膨胀集合O⊕C(r)中。显然，当τ=0 时，式（2）为O,A最近距离；当τ=1 时，式（2）为O,A最远距离；当τ=0.5 时，结合式（2）并用内插逼近的方法计算得到的O,A之间的距离，即为中位数距离，即DisM(O,A)为，亦为本文计算距离相似度所采用的距离（见图1 黑实线），则不同尺度两组群目标A1、A2，距离相似性度的计算公式可以表达为：

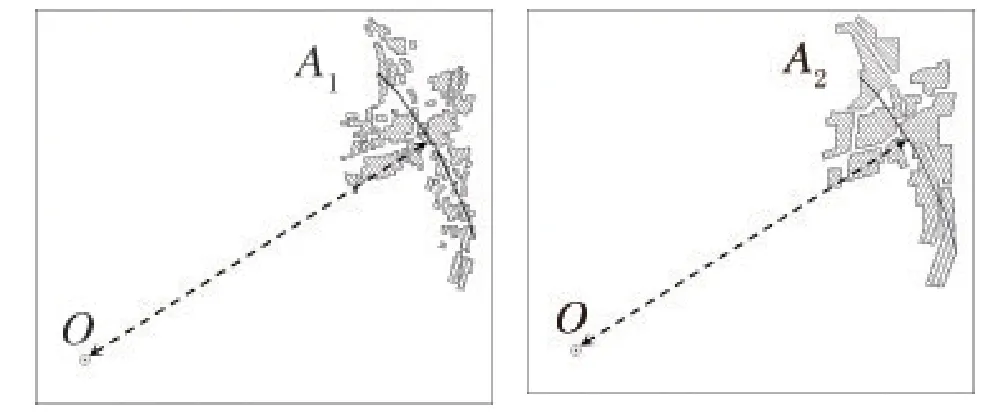
图1 尺度目标A1、A2及其中位数距离

1.2 方向相似度

方向关系描述了目标间方向分布的基本空间约束，常用于空间影像数据相似性评估和检索。邓敏等人提出了一种方向统计模型测对目标间方向分布的趋势[8]，可将其用于度量面群目标方向相似性。

设O为参考目标（单个点目标），A集合为群目标，并且令

式中：⊗为旋转因子，即以O点为圆心的射线，从标准方向开始以微小的角度β进行顺时针旋转；0 ≤τ≤1；θ(·)为一个度量函数，取值为0 或者交集面积；X(β)表示角度β旋转覆盖区域。

定义：

式中：Dir(O,A)为O、A的方向度量。

由式（5）可知，以微小的角度β进行旋转以至于集合A包含在旋转区域集合中。显然，当τ=0时，式（5）为O、A最近方位；当τ=1 时，式（5）为O、A最远方位；当τ=0.5 时，结合式（5）并用内插逼近的方法计算得到的O、A之间的方位，即为中值方向，记作DirM(O,A)，亦为本文计算方向相似度所采用的方向（见图2 黑实线），则不同尺度两组群目标A1、A2，方向相似度的计算公式可表达为：

图2 尺度目标A1、A2及其中值方向

1.3 形状相似度

利用形状特性可以快速、直观地检索目标。分形具有旋转、平移、比例不变性，与人的视觉判别较为一致，可较好地反映目标的局部和整体的自相似特征[9]，是一种度量形状相似度的一种很好的方法。基于这一形状度量方法，通过分形维数差异来表达面群目标的形状相似度。分形维数计算方法较多，其中，盒维数法最为常用。

将面群目标用边长为Size的小格子覆盖，将非空盒子计数为Cout；然后，将盒子的尺寸Size缩小，那么得到的Cout增多。当Size→0时，得到盒维数法。

定义：

式中：k为一常量；D表示目标的分形维数；Size为盒子大小；Cout为盒子数。

式（7）对数形式为：

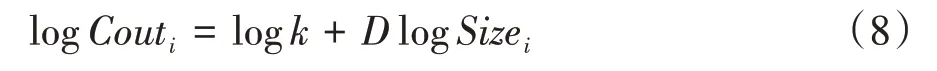
式(8)可以视为是以logSizei，logCouti为变量，以D为斜率的直线方程。

不同尺度两组群目标A1、A2，方向相似度的计算公式可表达为：

图3 尺度目标A1、A2分形维数计算图表

1.4 大小相似度

在相似性度量比较的中，除考虑目标的距离和形状，大小也是一个要考虑的重要因素，这里主要是通过面群目标的面积来体现。

对于不同尺度两组群目标A1、A2，大小相似度的计算公式可表达为：

2 实验与分析

相似性度量实验是在不同尺度（1:10 000 和1:50 000）选取同一区域一组群目标来进行的，见图4。利用式（1）～式（10），选择目标群的距离、方向、形状、大小等指标分别来计算相似度，结果，见表1 和表2。

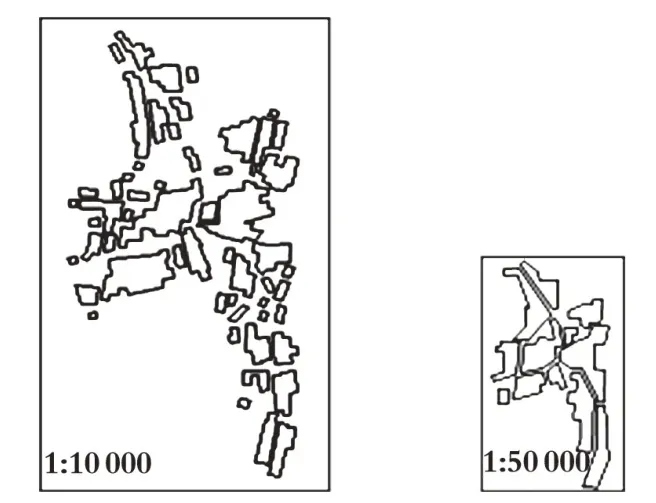
图4 相同区域不同尺度面群目标

表1 实验原始数据

表2 实验结果数据

从表1、表2和图1、图2可以看出：度量图形相似度时，距离相似度和方向相似度较好，形状相似度次之，大小相似度较差。实验结果表明，距离相似度和方向相似度与人眼判断结果较为一致，说明这两者度量方法很好地解决不同尺度同名群目标的相似性问题。

3 结论

以面群目标为研究对象，综合考虑空间分布和几何特征相似性的度量模型，并以多尺度面群建筑为实验数据，进行面群目标相似性测度实验，验证模型方法的普适性。通过对不同尺度面群数据进行相似性比较，发现基于距离模型和方向模型与人眼判断结果相一致，结果比较稳定。