涡轴发动机加速动态过程递推模型辨识

宋汉强，伍 恒，沈 勋，李本威

(1.海军研究院，上海 200436；2.海军研究院，北京 100161；3.海军航空大学航空基础学院，山东烟台 264001)

1 引言

航空发动机动态过程非线性模型在发动机状态监控、性能预估以及控制算法设计与仿真分析等领域有着至关重要的作用[1-3]。目前发动机建模方法主要有基于部件气动热力特性的解析法和基于实际数据的系统辨识法。解析法往往需要充足的发动机部件特性，计算较为复杂，需要进行大量的假设和近似处理，且存在迭代不收敛等问题，尚未应用到发动机实时状态监控与性能预估分析中。近年来，基于数据驱动的人工神经网络(ANN)、支持向量机(SVM)和极限学习机(ELM)等模型辨识方法得到了广泛应用。

针对建立航空发动机加速动态过程非线性辨识模型，Pogorelov等[4]利用动态神经网络对一个双轴燃气轮机差分形式的非线性动态模型进行辨识；Lyantsev 等[5]利用数值优化方法对燃气轮机加速模式下的非线性动态模型进行辨识；于同利[6]采用最小均方算法对发动机的加速过程进行辨识；潘鹏飞等[7-8]结合发动机飞行试验数据，利用三层前向人工神经网络分别对发动机的加减速瞬态模型及非线性动态模型进行辨识；王海涛等[9-10]先采用某型涡扇发动机地面台架试车数据辨识建立了其加速过程非线性Volterra-Laguerre 拓展模型，而后应用稀疏LSSVM辨识建立了某型涡扇发动机动态过程模型，并利用台架试验数据进行了辨识模型的验证、预测和递推估算，取得了不错效果。然而，对于复杂的模型结构，简单的最小二乘法的辨识效果往往不够理想，仍存在估计偏差，而神经网络算法往往训练时间过长，且容易陷入局部极小值。ELM[11-12]是单隐含层神经网络，但相比于传统的神经网络算法，其学习效率大幅提升，且非线性拟合能力要优于一些传统的ANN算法和SVM[13-14]。而将SVM中的核函数加入到ELM中形成的KELM算法[15-16]，只需对正则化系数和核参数的值进行优化选取即可得到稳定的非线性辨识效果。

鉴于上述分析，本文结合某型涡轴发动机工厂试车和台架验收试车数据，利用量子粒子群优化核极限学习机(QPSO-KELM)算法辨识建立基于非线性自回归(NARX)神经网络的发动机加速动态非线性模型，并进行了模型验证测试及递推估计应用分析。以期为进一步研究该型涡轴发动机加速控制规律优化并对发动机健康状态评估奠定基础。

2 基于QPSO优化的KELM算法原理

2.1 KELM和QPSO算法概述

ELM 是一种性能优良的单隐层前馈神经网络机器学习算法。为避免其输出产生随机波动影响模型的稳定性和泛化能力，Huang等[12-14]在ELM中加入SVM原理中的核函数，提出一种新的核极限学习机(KELM)。算法将随机矩阵转换为核矩阵，并用核映射代替随机映射。这样不仅提高了算法的非线性拟合能力，而且还使得算法具有更好的稳定性，也避免了极限学习机模型输出产生的随机波动。

SUN、宋汉强等提出的QPSO 算法[17-18]是在PSO算法的基础上引入量子力学原理，在量子空间中通过波函数ψ(y,k)而非速度和位置来描述粒子的状态。求解薛定谔方程，得到粒子在某一点出现的概率密度函数|ψ(y,k)|2。采用蒙特卡洛方法，可得粒子移动的搜索方程。由于算法中粒子搜寻的位置由概率密度函数确定，取消速度参数，使得算法不仅简单，而且稳定性好，具有较强的全局搜索和寻优能力。

2.2 基于QPSO的KELM特征参数优化流程

利用QPSO 算法优选KELM 的特征参数只包括正则化系数C和核参数σ两个，使得模型辨识效率较高。其具体优化流程为：

第一步：初始化。首先随机生成粒子种群，种群数量一般取30～50 即可。种群当中的每个粒子Li由一组正则化系数C和核参数σ组成，如式(1)所示。粒子中所有的元素都在[0，1]范围内随机初始化，并在计算适应度函数值之前根据不同参数的取值范围对初始化值进行还原。

第二步：适应度函数值的计算。粒子的适应度函数值计算采用预测输出与目标输出的均方根误差来实现，QPSO寻优的目标即为最小化适应度函数，如式(2)所示。

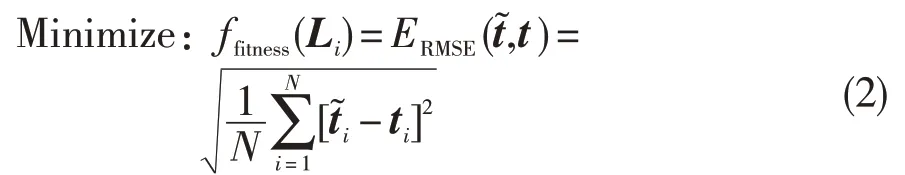
式中：ERMSE为均方根误差为模型的预测输出，ti为目标输出。

第三步：更新粒子的个体历史最好位置和种群历史最好位置，并重新计算每个粒子的局部吸引点和平均最好位置，再更新每个粒子的新的位置。

最后，重复上述步骤直到达到最大迭代次数。这样即可针对实际问题，得到KELM 优选的特征参数，再结合训练样本集，利用优选特征参数的KELM进行模型的回归辨识。

3 基于QPSO-KELM 的涡轴发动机加速动态过程递推模型辨识

3.1 加速动态过程递推模型辨识架构设计

Leontaritis 等提出的一种描述非线性离散系统的包含外源输入的非线性自回归移动平均(NARMAX)[19]神经网络模型可以逼近任意非线性动态系统，具有结构简单、非线性逼近能力强和收敛速度较快的优点，在航空航天航海领域受到了广泛的应用。其模型结构为：

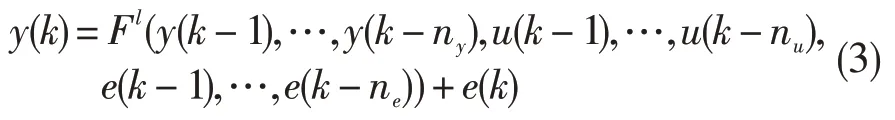
式中：u(k-i)(i=1,…,nu)、y(k-i)(i=1,…,ny) 和e(k-i)(i=1,…,ne)分别为系统的输入、输出和噪声，nu、ny、ne分别对应输入、输出和噪声的最大延迟；e(k)为均值为零的有限方差的白噪声；F是l=ny+nu+ne维的非线性函数。

由于实际情况下e(k)通常是未知的，因此式(3)可简化为式(4)的形式，即为基于外源输入的非线性自回归(NARX)[20-21]神经网络模型。

根据该型涡轴发动机地面试车采集的参数数据，可得表征发动机加速动态过程工作状态和性能的参数，主要有燃气发生器转子转速ng、发动机输出轴功率Pr和燃气涡轮后温度T5。发动机的调节规律是保持输出轴转速不变，并通过控制燃烧室的燃油消耗量Wf，从而实现发动机状态的改变。此外，输入参数还包括大气环境参数，即大气温度T0和大气压力p0。因此，该型发动机加速动态过程非线性映射表达式可描述为：

式中：ny1、ny2、ny3分别表示各输出参数的最大延迟，fKELM为需要辨识的非线性函数关系。

在式(5)表示的模型结构的基础上，考虑发动机的动态惯性和控制特点，设计输入输出参数的最大时延取值为ny1=ny2=ny3=nu=1，从而形成以ng(k)、ng(k-1)、Pr(k)、Pr(k-1)、T5(k)、T5(k-1)、p0(k)、T0(k)、Wf(k)和Wf(k-1)共10维作为输入向量，以ng(k+1)、Pr(k+1)和T5(k+1)共3维作为输出向量的模型辨识架构。设计学习机对基于NARX神经网络的发动机加速动态模型进行回归辨识。根据以上分析，该型涡轴发动机加速动态非线性NARX模型的输入输出参数如表1所示。

表1 加速动态非线性NARX模型的输入输出参数Table 1 Input and output parameters of acceleration dynamic nonlinear NARX model

3.2 基于QPSO-KELM 的发动机加速动态过程递推模型辨识方法

KELM 可以实现多输入多输出对象的模型辨识。令t ∈Rm代表表1 中输出参数组成的目标向量，x ∈Rn代表表1中输入参数组成的向量，则核极限学习机辨识加速动态过程递推模型的思想为：针对未知非线性函数t=f(x)，以及N个不同的独立样本，寻求函数，使得KELM 网络输出向量与实际的目标向量t 之间的均方根误差最小。

根据以上分析，基于QPSO-KELM 的该型涡轴发动机加速动态非线性NARX神经网络模型辨识的具体流程如图1所示。主要步骤为：

图1 加速动态非线性NARX模型辨识流程Fig.1 Acceleration dynamic nonlinear NARX model identification process

步骤1：建立该型涡轴发动机加速动态非线性NARX 模型辨识架构，并根据输入输出参数选取发动机工厂试车和台架验收试车样本数据组成模型辨识样本集；

步骤2：对选取的样本集进行平滑、滤波和归一化处理，并按照预定比例进行随机分组；

步骤3：设置好种群数量以及最大迭代次数等QPSO 算法的基本参数，利用QPSO 算法对KELM 的C和σ寻优；

步骤4：利用优选特征参数的KELM算法辨识建立发动机NARX 神经网络加速动态过程递推模型，并对辨识模型进行验证和测试分析；

步骤5：重复上述步骤，直到达到设定的最大随机样本分配次数，然后对比得到的各NARX 神经网络辨识模型输出参数的测试精度，选择其中稳定性最好、精度最高的模型为发动机加速动态过程递推模型。

4 辨识结果分析

4.1 模型辨识样本数据的选取与处理

本文研究的加速过程，是根据该型涡轴发动机工厂试车和验收试车技术规范中对发动机加速性能进行检查的过程，即从ng=25 000 r/min快速推油门杆至ng=32 000 r/min的发动机加速过程。选取涡轴发动机工厂试车和验收试车加速动态过程数据组成模型辨识的样本集，样本的采样时间间隔为0.091 s。模型输入输出参数数据根据表1并结合燃油消耗量和燃气发生器转子转速的变化范围选取。其中，样本集中的一组发动机验收试车加速动态过程数据如表2所示。

表2 发动机验收试车加速动态过程部分数据Table 2 Data of engine acceptance trial run in acceleration dynamic process

为便于讨论和对比分析，对数据进行了平滑和滤波处理[22]。根据选取的各样本参数的最大值和最小值，对相应的各样本参数数据进行归一化，并在模型输出时实施反归一化。采用辨识模型的预测值与实际测量值的相对误差范围及最大相对误差来评价所建辨识模型的精度。

式中：yt为试车过程中实际测量的发动机输出参数数据，yp为辨识模型预测得到的输出参数数据，Eref为相对误差。

4.2 模型辨识结果

根据上述发动机加速动态过程递推模型辨识方法，结合选取的样本集数据，采用QPSO 算法寻优KELM 的特征参数，通过优化确定KELM 的特征参数取值分别为：C=178.086 1，σ=0.301 7。核函数类型为Sigmoid核函数。优化完成后，利用优选特征参数的KELM对涡轴发动机加速动态过程递推模型进行回归辨识。

为验证辨识模型精度，分别将一组辨识用数据作为验证样本，一组非辨识用数据作为测试样本，输入到涡轴发动机加速动态过程递推模型中进行验证与预测分析。模型预测输出与实测数据的对比及不同样本点的相对误差分布如图2～图4 所示。从图中可得，辨识建立的涡轴发动机加速动态过程递推模型的输出参数ng、Pr和T5的验证和测试结果都良好地逼近了实测数据。其中，辨识用样本作为验证样本时，发动机各输出参数ng、Pr和T5不同数据点的最大相对误差分别为0.498%、0.935%和0.814%。非辨识用样本作为测试样本时，发动机输出参数ng和T5不同数据点的最大相对误差分别为0.761%和0.941%；输出参数Pr不同数据点的最大相对误差为1.377%。表明本文采用QPSO-KELM辨识建立的涡轴发动机加速动态过程递推模型精度较高，且具有一定的泛化能力。

图2 辨识结果误差分布(验证样本)Fig.2 Identification result error distribution(verification sample)

图4 辨识误差分布(测试样本)Fig.4 Identification error distribution(test sample)

分析误差产生的原因，可能是由于试车人员在不同试车过程中推油门速率不一致，再叠加环境因素及数据测量噪声的影响，使得类似加速动态过程的燃油流量变化率不同而导致样本分布不同，最后影响了辨识模型的预测精度。

4.3 模型递推估算应用分析

针对建立的发动机加速动态过程递推模型，如果已知类似加速动态过程的发动机的ng、Pr、T5、Wf以及大气环境参数的基准点数据，则可以通过递推估计的方式得到相应条件下的发动机加速动态过程响应，并估算出各输出参数随时间的变化曲线。

模型递推估算结构如图5 所示，其基本思路可描述为：根据某一时刻试车基准点数据中的ng(k)、ng(k-1)、pr(k)、pr(k-1)、T5(k)、T5(k-1)，结合当前时刻的Wf(k)、Wf(k-1)以及p0(k)、T0(k)，输入到辨识模型中递推得到下一时刻的输出量ng(k+1)、Pr(k+1)、T5(k+1)。将得到的输出量作为新的基准点，结合已知的Wf(k+1)、Wf(k)、p0(k+1)、T0(k+1)一起作为模型的新输入，依次递推求解下一时刻的输出，从而得到发动机整个加速动态过程的性能估算结果。

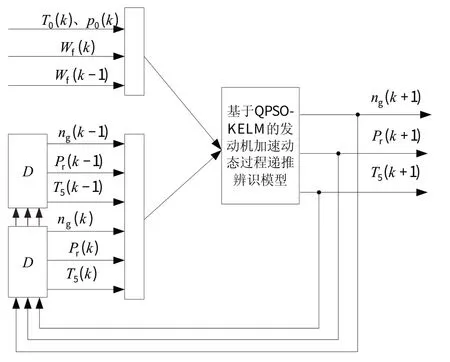
图5 发动机加速动态过程性能递推估算模型结构Fig.5 Performance recursive estimation model structure of engine acceleration dynamic process

根据本文辨识建立的发动机加速过程动态递推估算模型，选取一组辨识用数据并从起始数据点进行仿真，此后模型输出参数均采用递推求得的数据，由此可得各输出参数的递推估算结果与实测数据的误差分布如图6 所示。同样，再利用另一组发动机试车类似加速动态过程非辨识用数据进行预估分析，结果如图7、图8所示。

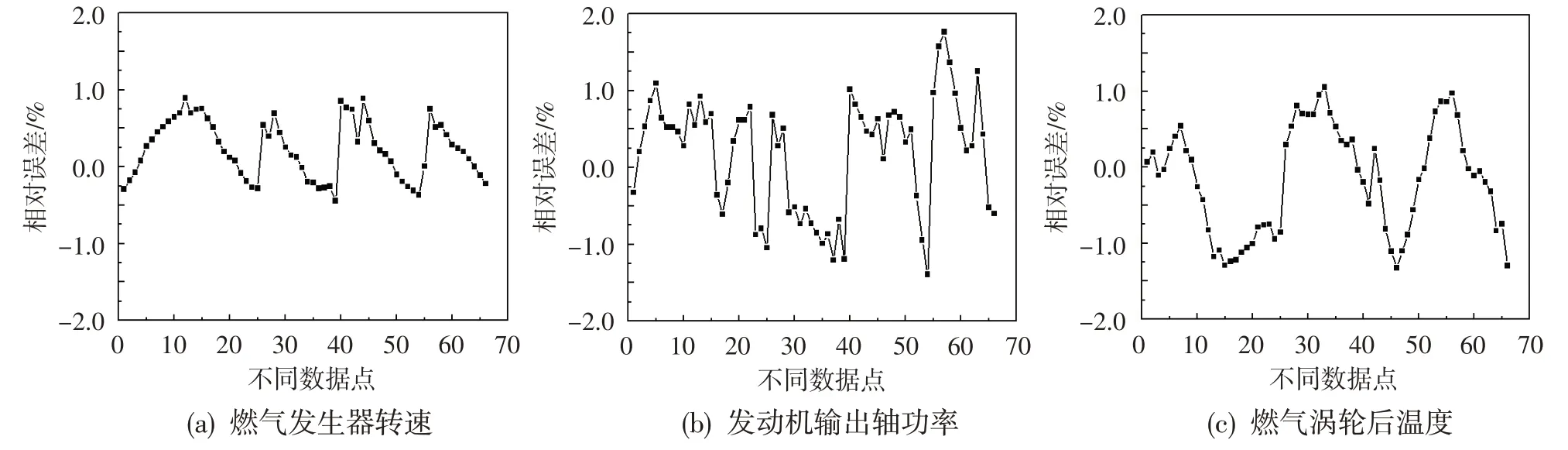
图6 递推估算结果误差分布(验证样本)Fig.6 Recursive estimation result error distribution(verification sample)

图7 递推估算结果(测试样本)Fig.7 Recursive estimation result(test sample)

图8 递推估算误差分布(测试样本)Fig.8 Recursive estimation error distribution(test sample)

从图6 可看出，发动机加速动态过程递推模型的输出参数ng、Pr和T5的递推估算结果与实测数据之间的误差比验证和测试过程的偏大，尤其是Pr和T5，相对误差超过0.5%的数据点明显增多。ng、Pr和T5的最大相对误差分别为0.893%、1.762%和1.323%。由图7、图8 可知，ng、Pr和T5的最大相对误差分别为1.139%、2.078%和1.629%。尽管模型各输出参数的递推估算结果与实测数据之间的误差有所增大，但各输出参数仍然较好地保持了其自身变化趋势，进一步说明辨识模型具有较高的精度。误差增大可能是由于将估算值作为基准点进行递推估算所产生的误差在不断的传播过程中累积，从而使得最终结果产生了相对较大的偏差。

综上，本文利用QPSO-KELM 辨识建立的涡轴发动机加速动态过程递推模型，不仅能满足实际应用的模型精度需求，而且还具有一定的泛化能力，可用于该型涡轴发动机的状态监控、性能预估及加速动态过程的仿真分析。

5 结论

结合涡轴发动机工厂试车及台架验收试车数据，利用QPSO-KELM 算法辨识建立了基于NARX神经网络的发动机加速动态过程递推模型，并进行了模型验证、测试及递推估算应用分析，可得如下结论：

(1) 采用QPSO-KELM辨识建立的涡轴发动机加速动态过程递推模型精度较高，且具有一定的泛化能力。辨识建立的发动机加速动态过程递推模型的输出参数燃气发生器转子转速、发动机输出轴功率和燃气涡轮后温度的验证和测试结果都良好地逼近了实测数据。其中，辨识用样本作为验证样本时，发动机各输出参数不同数据点的相对误差均未超过1%；非辨识用样本作为测试样本时，发动机各输出参数不同数据点的相对误差均未超过2%。

(2) 辨识用样本和非辨识用样本用于递推估算时，尽管模型各输出参数的递推估算结果与实测数据之间的误差比验证过程和测试过程有所增大，但采用递推估算方法得到的模型各输出参数仍然较好地保持了其自身变化趋势，进一步说明辨识模型具有较高的精度。

(3) 由于本文采用的是发动机地面试车数据，其进口条件(温度、高度等)在试车过程中变化不够充分。因此，开展相应的发动机高空试验或高空台模拟试验，获取变化更为充分的样本数据，以建立全飞行包线各区域的加速动态过程辨识模型值得进一步研究。