卷积神经网络应用于雷达目标检测

赵晨帆，王 萍，邢冠培，叶 舟，王 锦

（上海航天电子技术研究所，上海，201109）

0 引 言

近年来，随着无人机等低空、慢速、小型目标（下文简称低慢小）飞行器的快速发展与低空空域管制的逐渐开放，低慢小目标违规飞行的事件日益增多，产生了较大的负面影响[1]。因此，对复杂环境下的低慢小目标进行探测、定位和跟踪已经成为了近期的研究热点之一。其中，准确地判断观测区域内有无目标成为重要前提。对脉冲多普勒雷达进行信号处理时，通常先将收到的回波信号进行匹配滤波处理和多普勒处理，最后依据奈曼-皮尔逊准则设计恒虚警（Constant False Alarm Rate，CFAR）检测器进行门限判断，判别目标的有无[2]。CFAR 检测器在简单场景中，能较好地从背景中分离出目标，但在城市、郊区、边境防走私等复杂环境中进行目标检测时，回波信号中往往混有散射特性迥异的杂波，此时CFAR 检测器的检测性能有所下降。

而卷积神经网络（Convolutional Neural Network，CNN）在图像处理中得到了广泛应用，在图像分类[3,4]中取得了很好的成果，在目标检测方面的准确度也有很大的提高，如手写数字识别[5]、人脸识别[6]等。一方面是因为卷积神经网络提取了高层特征，提高了特征的表达能力；另一方面是因为卷积神经网络将目标检测的关键步骤融合在同一模型中，通过端到端的训练，进行整体的功能优化，增强了特征的可分性[7]。

本文选择了噪声和其他3 种不同的杂波环境，将信号处理过程中的距离——多普勒频谱作为“图像”，用CNN 代替CFAR 检测器进行目标检测，并与相同条件下CFAR 检测器的检测结果进行对比。

1 传统雷达目标检测

1.1 传统检测方法

传统的脉冲多普勒雷达信号处理包括3 个模块，即：匹配滤波器、多普勒处理和CFAR 检测器。CFAR检测器的输入为回波信号的多普勒维数据，对每个多普勒单元进行单独检测，处理流程如图1 所示。

图1 传统雷达信号检测Fig.1 Traditional Radar Signal Detection Block Diagram

目前，众多学者已经进行了大量的雷达杂波统计模型研究。从统计理论进行分析，可以将杂波作为一种完全随机的信号，用适当的概率统计分布模型来描述，如瑞利分布、韦布尔分布和K 分布等[8,9]。

a）瑞利分布通常用于描述气象杂波、箔条干扰、低分辨率雷达的地杂波，对于低分辨率雷达的海面杂波幅度分布一般也服从瑞利分布[10]。用x 表示瑞利分布杂波回波的包络振幅，则x 的概率密度函数为

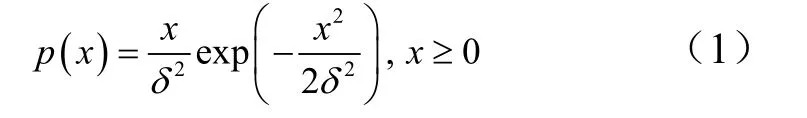
式中 δ 为杂波的标准差。

b）对于近距离的地物杂波，或海杂波幅度起伏较为均匀、高分辨率雷达和低入射角的情况下，采用韦布尔分布来描述杂波较为合适。因此，韦布尔分布模型能很好地描述地物杂波、海杂波和云雨杂波等。如果用x 表示韦布尔分布杂波回波的包络振幅，则x 的概率密度函数为

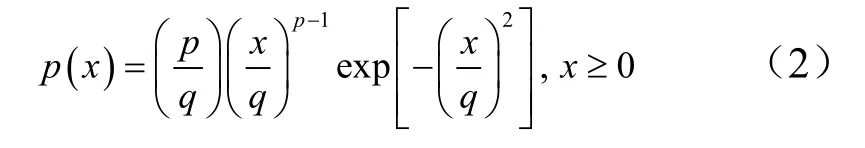
式中 p 为杂波分布的均值；q 为分布的偏斜度。

K 分布作为一种新构造的混合模型，适于描述多种高分辨、低擦地角的地杂波和海杂波，是目前公认能精确反映雷达杂波的模型。如果用x 表示K 分布杂波回波的包络振幅，则x 的概率密度函数为

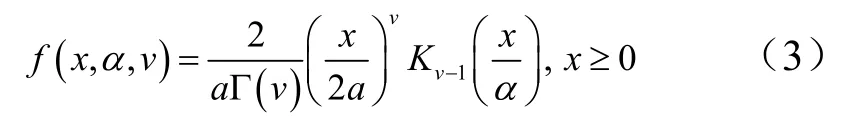
式中 v 为形状参数；a 为尺度参数；Γ( ⋅)为伽马函数；Kv(⋅)为第二类修正贝塞尔函数。

1.2 二维CA-CFAR 检测器

在实际的雷达检测环境中，距离维和多普勒维同时存在噪声和杂波，因此CFAR 检测时，需要同时估计距离和多普勒维上的参考单元，这样获得的背景噪声水平估计也更加准确有效。本文采用如图2 所示的矩形窗二维CA-CFAR 检测方法，在距离维选取3 个保护单元和4 个检测单元，在多普勒维选取1 个保护单元和2 个检测单元。其中保护窗口的设置是为了防止背景中包含目标的部分信息引起背景的统计计算不正确。与一维CFAR 检测流程相比，二维CA-CFAR 检测只是在检测算法上进行改进，整体流程没有变化。

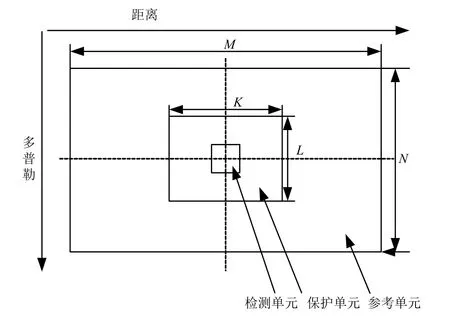
图2 矩形窗二维CA-CFAR 检测器Fig.2 Rectangular Window Two-dimensional CA-CFAR Detector

2 利用卷积神经网络进行信号检测

2.1 检测方法

传统的目标检测是二元假设检验，也可以视为二元分类（即目标存在或目标不存在）。在高斯白噪声背景下，有目标和无目标时的多普勒频谱如图3 所示。若将多普勒频谱视为图像，这种图像可以分为有目标和无目标两类，再利用CNN 代替CFAR 检测器进行目标检测。图4 为利用CNN 进行目标检测的检测流程图。

图3 高斯白噪声背景下的多普勒频谱Fig.3 Distance in the Background of Gaussian White Noisedoppler Spectrum

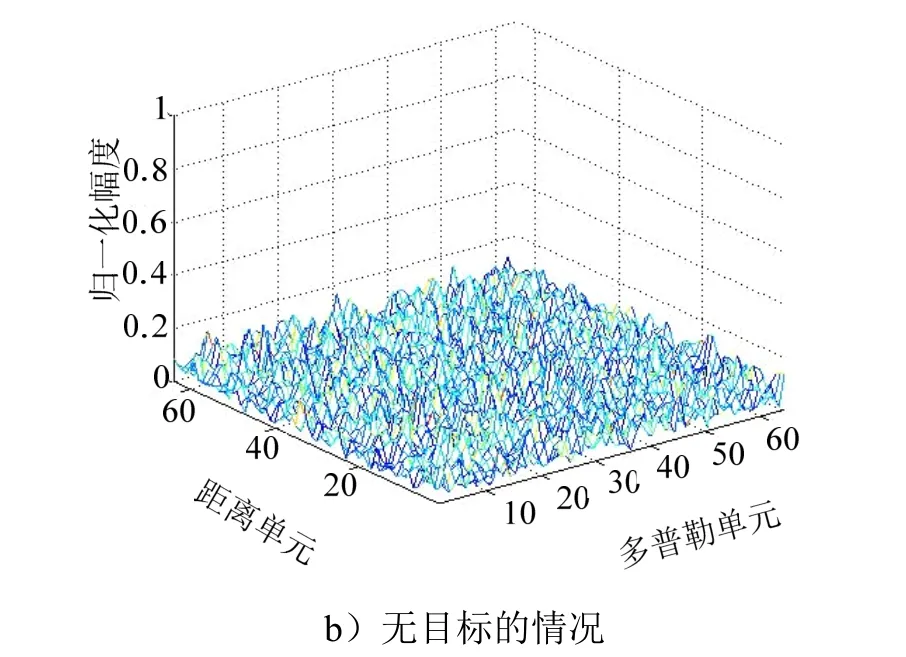
续图3

图4 利用CNN 进行雷达目标检测流程Fig.4 Using CNN for Radar Target Detection Flow Chart

2.2 卷积神经网络

CNN 本质上是一种特殊的多层感知器或前馈神经网络，其低隐层由卷积层与池化层交替组成，高层是全连接层。原始图像经过卷积层与池化层，得到特征图，实现目标特征提取。特征图再被作为全连接层的输入，与多层感知器与分类器相连接[11]。本文所采用CNN 的网络结构如图5 所示，有2 个卷积层，2 个最大池化层和2 个全连接层。

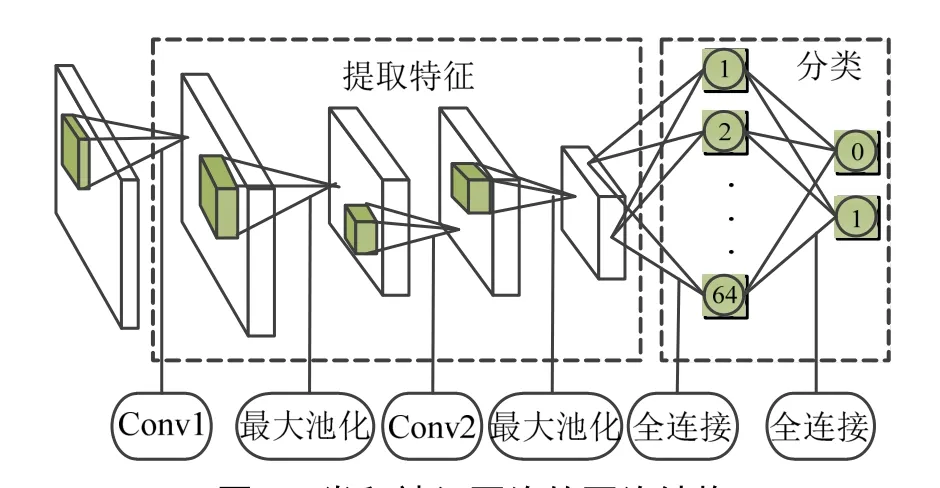
图5 卷积神经网络的网络结构Fig.5 The Network Structure of the Convolutional Neural Network Used

对于图4 中描述的目标检测，CNN 检测器的输入是多普勒频谱样本。多普勒频谱样本的大小由滑动窗口的大小确定。第1 个卷积层中有32 个卷积核，每个卷积核的大小为5×5；第2 个卷积层中有16 个卷积核，每个卷积滤波核的大小为3×3，卷积层均采用Relu 激活函数。每个最大池化层的池化区域大小为2×2。第1个全连接层有64 个输出神经元，第2 个全连接层是输出层，利用softmax 函数进行分类运算，有两个输出神经元，表示目标存在和目标缺失。

3 仿真及结果分析

3.1 仿真数据

对雷达回波信号进行仿真，采用64 组脉冲信号接收目标回波、噪声和杂波。信号脉宽为50 µs，带宽为4 MHz，采样频率为8 MHz，脉冲重复频率为2.7 kHz。将收到的回波依次经过匹配滤波处理和多普勒处理，得到回波的多普勒频谱。

将频谱中有目标回波的部分，划分出64*64 大小的矩阵块，再选取没有目标回波的64*64 大小的矩阵块。将这两个64*64 的矩阵视为图像，并分别标记为1和0，表示回波的多普勒频谱中有目标和无目标的情况。产生20 000 组多普勒信息矩阵，其中10 000 组有目标，目标的距离和速度为随机产生，其他10 000 组无目标。从这些矩阵中随机选取出4 000 组作为训练集样本，用CNN 进行训练，剩下的16 000 组作为测试集样本，检测训练的网络准确率。

同时，分别对相同环境背景下的回波信号做二维CA-CFAR 检测，将检测后的检测概率和CNN 的检测概率进行对比。

3.2 白噪声背景下的检测

在确定信噪比为9 dB 的条件下，分别改变训练次数为20 次、50 次、80 次和150 次，得到训练结果如图6 所示，进行CFAR 检测得到检测概率为0.8699。由图6 可以看出随着训练次数的增加，网络的检测概率逐渐提高，训练次数达到150 次后的检测概率比相同条件下CFAR 检测的检测概率高。

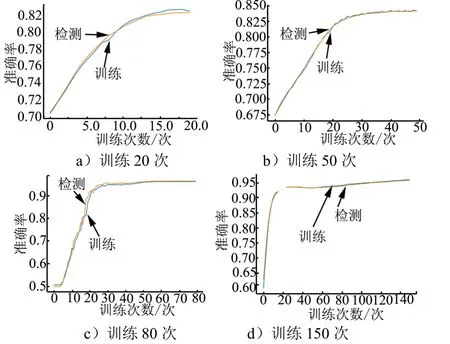
图6 不同网络学习次数的准确率变化情况Fig.6 Accuracy Rate Change Graph of Different Network Learning Times

为了确保能够获得稳定的训练结果，选择训练150 次，改变信噪比，将相同条件下传统的CFAR 检测和CNN 的检测结果进行比较，结果如表1 所示。

表1 不同信噪比下CFAR 和CNN 检测概率Tab.1 Detection Probability of CFAR and CNN under Different SNR

由表1 可以看出，CNN 的检测概率随着信噪比的增加而增加，且在同等条件下，检测概率优于CFAR检测的检测概率。

3.3 杂波背景下的检测

3.3.1 瑞利分布杂波背景下的目标检测

仿真以瑞利分布的杂波为背景的雷达信号，进行多普勒处理后的多普勒频谱如图7 所示。

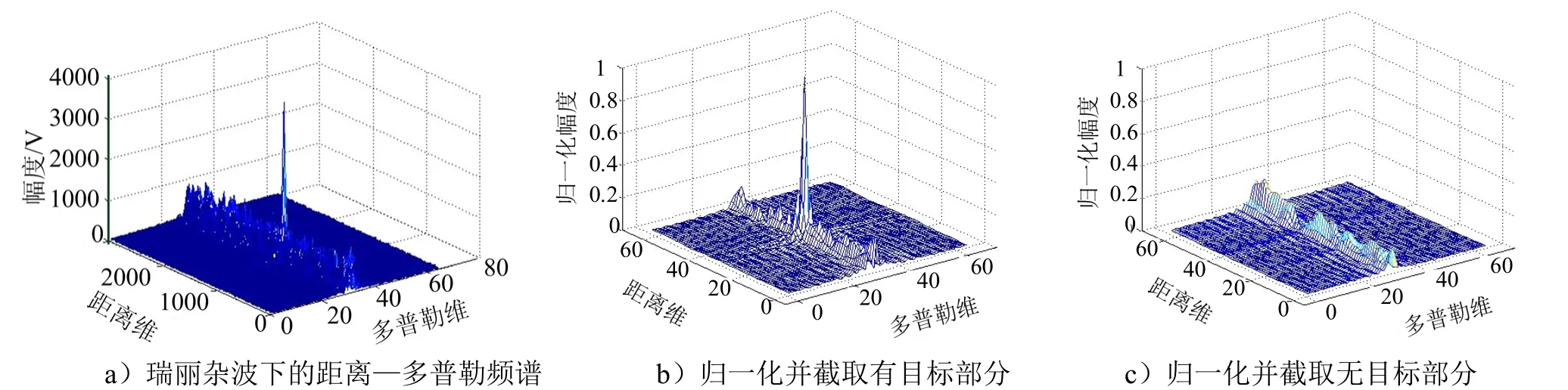
图7 瑞利分布杂波下的频谱Fig.7 Spectral Diagram under Rayleigh Distribution Clutter

设定瑞利分布的标准差为0～5 的随机数，信杂比分别为6 dB、9 dB 和13 dB，产生含有瑞利分布杂波背景的训练集和测试集数据。调整卷积神经网络中优化器的学习率，对数据集进行训练。图8 为训练中的准确率变化曲线，对比CFAR 和CNN 的检测概率结果如表2 所示。

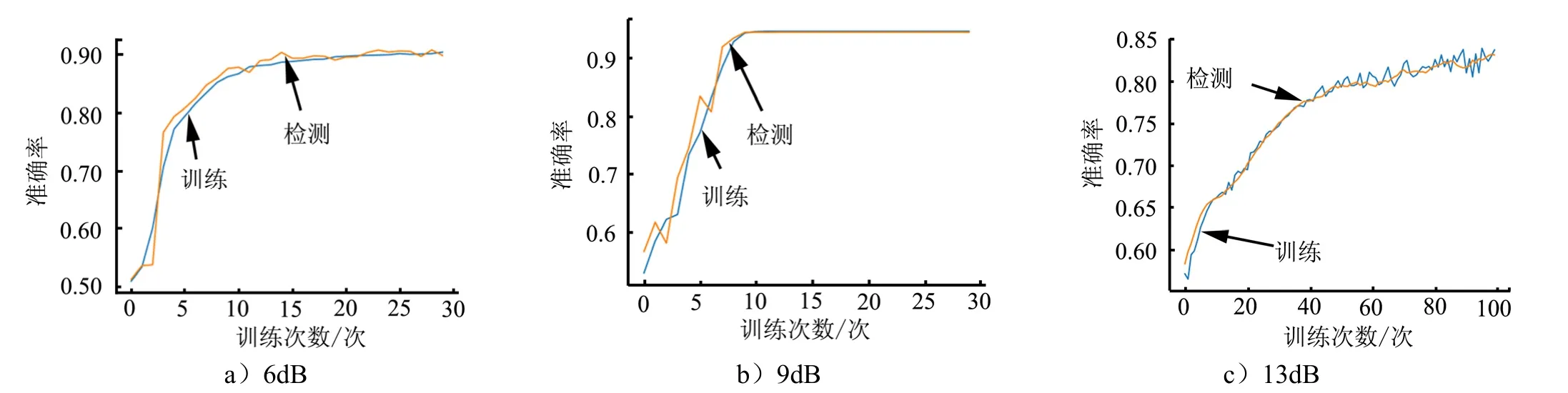
图8 网络学习的准确率变化曲线Fig.8 Network Learning Accuracy Curve

表2 瑞利杂波环境中CFAR 和CNN 检测概率对比Tab.2 Comparison Table of CFAR and CNN Detection Probability in Rayleigh Clutter Environment

3.3.2 韦布尔分布杂波背景下的目标检测

仿真以韦布尔分布的杂波为背景的雷达信号，进行多普勒处理后的多普勒频谱如图9 所示。

图9 韦布尔分布杂波下的频谱Fig.9 Spectral Diagram under Weibull Distribution Clutter

设定韦布尔分布的均值为1.5～6.5 的随机数，偏斜度为0.5～5.5 的随机数，信杂比分别为6 dB、9 dB 和13 dB，产生含有韦布尔分布杂波背景的训练集和测试集数据。调整卷积神经网络中优化器的学习率，对数据集进行训练。图10 为训练中的准确率变化曲线，对比CFAR 和CNN 的检测概率结果如表3 所示。

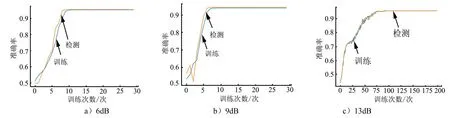
图10 网络学习的准确率变化曲线Fig.10 Network Learning Accuracy Curve

表3 韦布尔杂波环境中CFAR 和CNN 检测概率对比Tab.3 Comparison of CFAR and CNN Detection Probability in Weibull Clutter Environment

3.3.3 K 分布杂波背景下的目标检测

仿真以K 分布的杂波为背景的雷达信号，进行多普勒处理后的多普勒频谱如图11 所示。

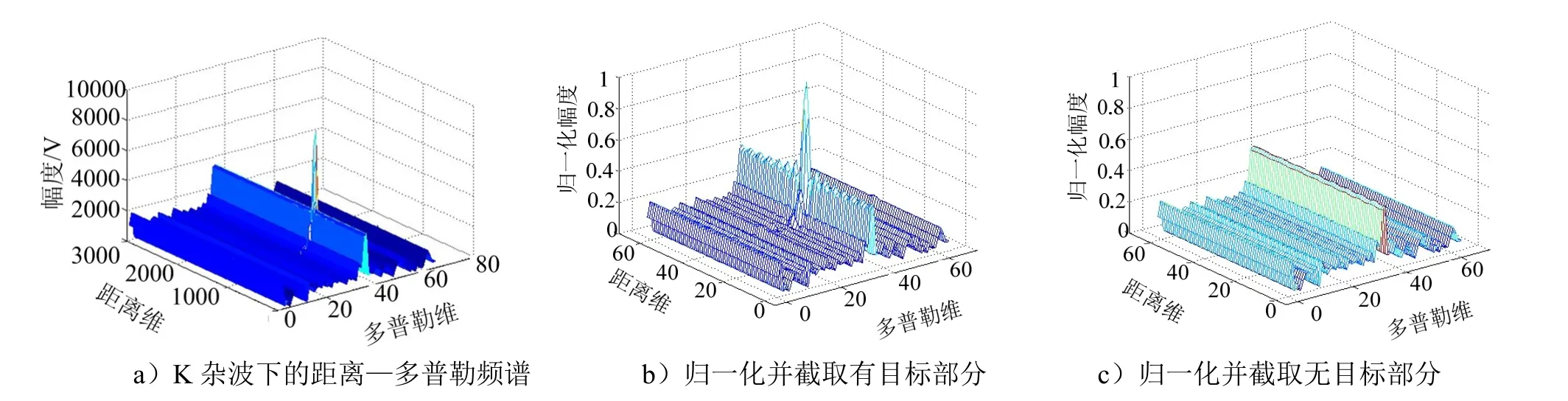
图11 K 分布杂波下的频谱Fig.11 Spectral Diagram under K-Distribution

设定K 分布的相关系数为0～5 的随机数，信杂比 分别为6 dB，9 dB 和13 dB，产生含有K 分布杂波背景的训练集和测试集数据。调整卷积神经网络中优化器的学习率，对数据集进行训练。图12 为训练中的准确率变化曲线，对比CFAR 和CNN 的检测概率结果如表4 所示。

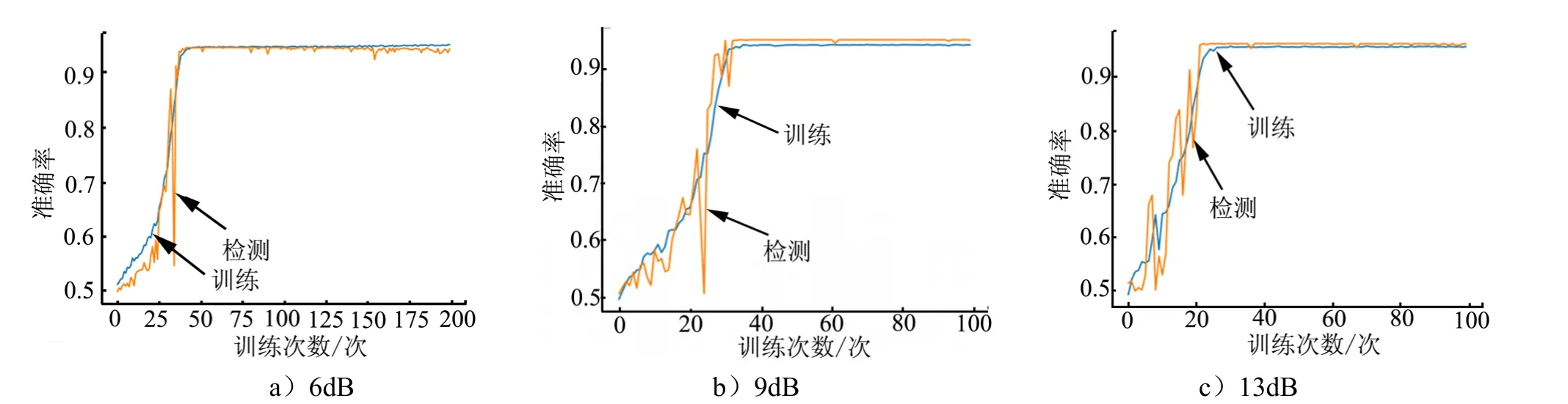
图12 网络学习的准确率变化曲线Fig.12 Network Learning Accuracy Curve

表4 K 分布杂波环境中CFAR 和CNN 检测概率对比表Tab.4 Comparison table of CFAR and CNN Detection Probability In K-Distributed Clutter Environment

3.4 CFAR 和CNN 进行目标检测的结果对比

对比3.3.1 节～3.3.3 节的仿真结果可以发现相同的环境背景下CNN 的检测概率普遍高于CFAR 的检测概率。在信噪比（或信杂比）较低时，检测概率有明显的提高，而信噪比（或信杂比）较高时，检测概率平均提高0.01。将不同杂波环境中的检测结果进行比较，瑞利分布和K 分布的杂波环境下，CNN 的检测概率提高较明显。

对多目标的检测，一般会采用GO-CFAR 检测器或SO-CFAR 检测器，可能会引起一定的恒虚警检测损失。例如GO-CFAR 在杂波边缘环境中，能保持较好的虚警控制能力，但同时在多目标环境中会出现“遮蔽效应”；而当干扰目标只位于前窗或者后窗时，SO-CFAR 能很好地分辨目标，但同时它并不能很好地控制虚警率[12]。然而，CNN 将多普勒频谱作为图像进行处理，可以一定程度的避免CFAR 带来的检测损失。

在算法复杂度的对比方面，CNN 的时间复杂度和空间复杂度可以分别根据式（4）和式（5）进行计算。

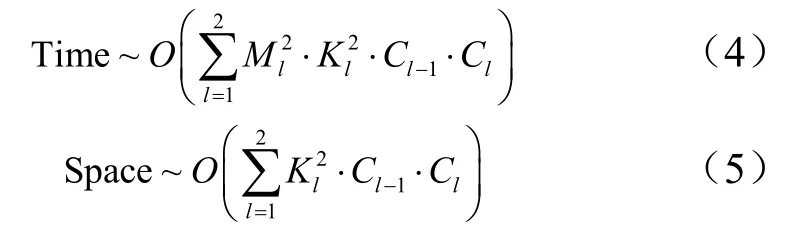
式中 M 为每个卷积核输出特征图的边长；K 表示每个卷积核的边长；Cl-1为上一层的输出通道数；Cl为本卷积层的卷积核个数即输出通道数。比较本文使用的CNN 和二维CA-CFAR 的算法复杂度，发现CNN 的时间复杂度稍高。但伴随GPU 等硬件运算平台的使用，CNN 比CFAR 算法复杂度稍高的问题可以通过硬件平台来解决。

4 结束语

针对脉冲多普勒雷达在复杂环境中，检测低慢小目标时存在多种杂波干扰、信杂比低等问题，本文提出用卷积神经网络代替传统信号处理中的 CFAR 检测器进行检测的方法。分别在高斯白噪声、瑞利分布杂波、韦布尔分布和K 分布的环境背景下，进行不同信噪比或信杂比的目标检测对比试验。仿真结果表明在相同环境中，卷积神经网络比二维CFAR 检测器具有更高的检测概率，检测概率至少提高0.01。