“学会打太极”

顾琴芳

摘 要：“让学”强调要留足可以供学生探讨数学问题的空间与时间，体现了生本化教学的思想。“引思”是在“让学”前提下对学生数学思考、探究过程的引领、指导与帮助。在“让学引思”模式下的小学数学课堂，理应将过去提倡的一些有价值的做法整合起来，形成一个辩证的课堂支持系统，帮助学生打造一个有效的探究去向，在协同中阐述新课程理念。

关键词：小学数学；让学引思；生本化

记得上世纪末笔者刚参加工作的时候，启发式教学红遍大江南北，但后来也有不少教师感慨：“如果学生启而不发，那我们该怎么办呢？”进入新世纪，随着“新课程”名称的出现，“生本化教学”逐渐涌入教师的视线，慢慢地，又有人呼吁：如果把学生捧上天，我们老师还有什么地位呢？再后来，“有效教学”、“思维课堂”、“核心素养”又成为课改的关键词。最近，笔者发现不少地方兴起“让学引思”的热潮，笔者认为“让学引思”较全面地反映了师生之间应该有的关系，给教学改革带来了一片崭新的天地。

“让学引思”包括“让学”与”引思”两个元素，“让学”强调的是教师要留足可以供学生思考、探讨数学问题的空间与时间，使其有机会学，想学，这体现了生本化教学的思想。“引思”是在“让学”前提下对学生数学思考、探究过程的引领、指导与帮助，这其实就是实施启发式教学。结合自己的学习与实践，以下谈谈小学数学教学中的“让学引思”策略，与同行探讨。

一、充分考虑课时需要，“让”得精准才能“促”到本真

课时教学的学习目标为“让学引思”提出了需求与方向，但是现实中常常出现教学行为与教学目标发生偏离的情况。以计算教学为例，在目前的课堂教学中，对算理的探究仍没有引起足够的重视，不少教师还是以僵化的法则教学替代有意义的算理教学，甚至以让学生背诵口诀为首要任务，严重偏离了新课程提出的“让学生理解与融会贯通”的方向。所以无论是“让学”还是“引思”，都不能背离课时目标的需求。

由上可见，对于这部分内容的教学，教师如果全盘控制起来，让学生机械地去识记计算法则，那学生只能沦为计算方法的奴隶，此时教师的“让学”应着眼于算理，着手于用已有经验解决新问题情境，再总结出计算法则。显然这样的计算法则是经过“酝酿的米酒”，他的本质是“大米淀粉”，也就是算理。

二、及时营造“愤悱”氛围，“让”出疑惑才能“引”发深思

曾经何时，老师们喜欢煞费苦心地设计一些动人的情境来吸引学生，尤其在多媒体时代，声、光、电为课堂提供了足够的技术支撑，似乎也调动了学生的参与热情。但这种情境对于教学的影响往往只是一种外部兴趣，并没有真正涉及对问题本质下的热爱。打个比方：家长给生病的孩子吃药时会在药里加糖，此时孩子只是对糖有兴趣，一旦糖撤消，那学生会更不肯吃药——这就是情境教学处理不当所造成的副作用。在“让学引思”的教学思路下，“让学”必须指向学习内容本身，引思也应该围绕教材内容而展开，任何外在的吸引充其量是弱化学生学习兴趣的“糖”。

记得在引导学生探究 “3的倍数的特征”的时候，笔者设计了这样一个训练序列：第一步，请说说能被2、5整除的数的特征；第二步，观察下列数字，分析他们能否被3整除，并发现他们的特点：6，36，516，8，38，9，69，33，93，123，423；第三步，.根据上述研究，我们能否得出能被3整除的数的特征？可以发现，这是笔者设计的一个思维陷阱。由于受能被2、5整除的數的特征规律的影响，加上教师刻意安排了一些特殊的数字来让学生研究，使得有很多学生马上进入了“圈套”，他们果断地认定：能被3整除的数的特征是个位数字能被3整除。

师：很好，大家看到了这跟2、5很类似，从而能总结出同样的规律，那么这样的总结是否真的正确呢？大家的结论是不是对所有整数都符合呢？

众生：这……难道……（疑惑不解，思忖着老师是不是又耍了什么花招）

师：我们要推翻刚才所说的规律，只要——

众生：（接）举出反面例子。

师：那谁能举出一个反面例子呢？

生1：老师，15是的，因为15能被3整除，但个位上的5不是3的倍数。

生2：老师，27能被3整除，但个位数7不是3的倍数。

（这时，学生纷纷举起了手，而且发现能推翻刚才结论的数字很多，开始认定刚才的思考是一种错误。）

师：不过，有些数还是可以只看个位上的数字而确定能否被3整除的，有些数就不能，都是哪些数呢？

生3：老师，我发现了象一位数，还有两位数中“3Δ”、“6Δ”、“9Δ”这样的数可以。

生4：对，这些数其实就是每一位上的数都能被3整除。

师：好，那么两位数中如果不符合每一位上的数都能被3整除，那他就一定不是3的倍数吗？

众生：好像也不是……

俗话说：“恨之深，爱之切”、“吃一堑，长一智”。在课堂教学中，这种失败的探究使学生面临“山穷水尽”的“恨”与不满之中，经由教师的巧妙引导，学生又能慢慢打开思路，迎来“柳暗花明”。这样的教学最能让学生产生心灵的震撼，使兴趣、知识与技能在峰回路转中豁然开朗。由此可见，教师通过“让学”，使学生得出疑惑，再通过“引思”来化解学生的疑惑，这样的教学过程充满了戏剧性，也给课堂带来了无限的生机。

三、巧于深入层层拓展，“引之有方”才能让出深度

教材只不过是学生学习知识的一种普遍化工具，“用教材教”的理念为我们开展有效的“让学”与“引思”提供了一定的底气。比如对于三角形的面积公式的探究，一般教材只给出利用两个全等三角形拼成平行四边形一种方法，但我们尽可以再进行深化：

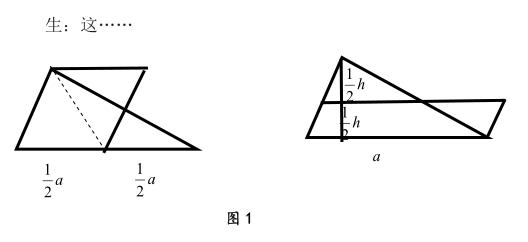
经过上述引思，学生终于发现三角形的面积还可以通过计算底边的一半再乘高得到，甚至可以先算出高的一半再和底边相乘得到。具体思路如图所示，这里三角形的面积不再是“同底等高的平行四边形面积的一半”这样的呈现形式，而是等于“高不变条件下取底边的一半形成的平行四边形的面积”和“底边不变条件下取一半高所形成的平行四边形”，这样的创新研究也同样能得到完全正确的答案。通过三种方法的研究，学生对于三角形面积公式的得出变得更为灵活与灵动，知识掌握更为牢固。

在开放的时代，学生的思想都非常活跃，他们的智慧远不是单一的思路可以框定的，这就需要我们大胆地“让学”，巧妙的“引思”，才能使知识形成的过程充满着创新的智慧，充盈着灵气的光輝。

四、充分尊重学生需求，“引”之灵活更显“让”得灵动

课堂是千变万化的，一旦教师事先决定了该在何处“让学”，那么教师的“引思”就会围绕“让学”的重点而展开，这并不是说教师必须完全按照事先设计来照本宣科，相反，只有随机应变的“引思”才能使“让学”变得灵动而有价值。

比如在圆柱体体积的探究过程中，有学生提出：为什么长方体体积是长、宽、高之积，而圆柱体体积却不是几条线段长度之积呢？笔者发觉此时学生的疑问带有普遍性，这正是相互比较进行知识融合的一个极好时机。于是笔者引导道：圆柱体与长方体是不同的物体，但有人发现他们的面积之间有着密切联系，你认为这种联系体现在哪儿？此时，有学生发现：其实长方体的体积也可以看成底面积乘高。教师就问他为什么？他说长方体中的长乘宽其实正好是长方体的底面积，所以长方体体积也适用底面积乘高。于是教师又趁热打铁：那么长方体体积可以看成三条线段之积，那么这在圆柱体中也成立吗？于是又有学生发现，原来圆柱体体积可以看成以“半径×半径×高×π”，就是某个特殊长方体体积的π倍，是一个怎样的长方体呢？在教师的引导下，学生纷纷尝试画图，尽管立体图形绘制的难度较大，但还是有不少学生画出了这个长方体，从而使长方体与圆柱体的体积之间产生了必然的联系。

如针对图2（右）的思考题：在一个底面为正方形的长方体立柱中切出一个最大的圆柱体，那么圆柱体体积与长方体体积之比是 。假如学生对图2（左）有充足的探究，那么不但能理解圆柱体体积与对应长方体之间的关系，还能很快找到解题思路：设图2（左）中长方体的体积为X，那么对应的大圆柱体体积为πX，对应的图2（右）中的大长方体体积为4X，所以这道题的答案应为π：4。显然，教师在教学中的充分“让学”，体现在“引思”过程中的不拘一格，让学生实现“条条道路通罗马”，从而可以以最优方案来解决特殊的问题。

由上可见，“让学”与“引思”正像打太极拳时的两只手，两手同时环抱一个气团，一手拎时另一手托，一手跑时另一手追，一手回时另一手相应地退，两手互相配合，协同作战。“让学”与“引思”是一对矛盾，在不断碰撞中走向成熟，达成和谐。在“让学引思”模式下的小学数学课堂，理应将过去提倡的一些有价值的做法整合起来，形成一个有效的探究去向，在协同中阐述新课程理念，既实现有效的启发式教学，也达成有价值的生本化教学，最终实现核心素养的提升。

参考文献

[1]“提问”——让课堂更精彩[J].孙乃群. 小学教学参考.2012（05）

[2]浅谈素质教育课堂教学和评价[J].梅友荣，施大瑜. 小学教学参考.2006（18）

[3]李芳.让学促思开拓教学新视角[J].基础教育研究，2016，（23）