一种改进的深度网络残差学习的图像降噪方法

靳华中，刘 阳，叶志伟

(湖北工业大学计算机学院，武汉 430068)

1 研究背景

降噪是图像处理中的一个重要应用，是图像处理中的一个经典逆问题.图像降噪的目的是尽可能地将噪声信号从受污染的图像中分离出来，并去除噪声信号，保留真实图像信息，带来更好的视觉效果.给定一个加性高斯白噪声模型，它可以表示为y=x+v(x表示原图像，v表示噪声).图像降噪是从带有噪声的图像y中恢复干净的图像x.尽管在过去几十年中已经提出了许多图像降噪算法，但由于当前深度卷积神经网络(deep convolutional neural network，DCNN)方法比传统的降噪方法降噪效果更优[1-4]，因此基于深度学习的算法成为当前研究图像降噪的热点之一.

DCNN方法将图像降噪作为一个监督回归问题来处理，有效的利用了外部先验信息.通过大量成对干净-噪声图像，学习得到一个高复杂度的多层网络结构约束函数，将学习外部先验条件的方式推向极限.DCNN图像降噪方法的优势主要体现在两个方面：一方面，DCNN具有很深的层次结构，可以有效地提高图像特征挖掘的能力和灵活性；另一方面，深度学习在训练过程中，采用正则化方法、RELU激活函数、批标准化处理等方法，加快了训练效率，提高降噪性能.

文献[5-6]利用DCNN方法进行图像降噪时，都获得了较为显著的降噪效果，但这些方法都存在一个明显的缺点：它们只针对某个特定水平的噪声建立降噪模型，在图像盲降噪中受到较大的限制.在解决图像盲降噪方面，FC-AIDE方法能够估计噪声的未知水平，但是网络参数的训练是在监督训练和自适应条件下微调得到的，其计算成本相对较大[7].降噪卷积神经网络(denoising convolutional neural network，DnCNN)利用残差学习方法进行图像降噪，该方法采用残差学习来估计残差图像，即噪声图像与潜在干净图像之间的差异[4]，解决了噪声水平未知的高斯降噪问题.受DnCNN的启发，本文提出了一种反卷积降噪神经网络(denoising deconvolution neural network，DnDNN).在本文构建的网络结构中，每一个隐藏层包括卷积运算和反卷积运算，卷积运算是提取图像的特征信息，包括边缘、线条等特征，反卷积运算是复原图像，复原到卷积之前图像的尺寸，最后一层做全连接，作为输出层.本文方法利用反卷积网络重构图像的方法进行降噪，在模型训练过程中引入残差学习.残差学习后得到的是纯噪声图像，纯噪声图像包含的信息比干净图像的少，训练起来更简单，效果更好；利用反卷积网络重构图像进行图像降噪的方法需要的网络层数更少，而且还能加快网络的收敛速度，提高降噪性能.

实验表明，在已知噪声强度级别的高斯降噪中，本文方法比现有的基于深度学习方法BM3D[8]、WNNM[9]的降噪效果好，比DnCNN方法的收敛时间短.对于噪声强度级别未知的高斯降噪，本文方法也取得较好的降噪效果，其盲降噪方法比针对特定噪声级训练特定模型的BM3D[8]和TNRD[10]的降噪方法性能更优.本文的主要工作总结如下：1) 提出了一种改进的深度网络残差学习的图像降噪方法；2) 本文提出的方法不仅能够提高残差学习的效率，加快训练速度，而且能够进一步提高降噪性能；3) 本文提出了一种新的损失函数计算方法，缩短了模型训练的收敛周期.

论文的其余部分组织如下：第2节简要介绍了相关工作.第3节首先介绍了提出的DnDNN模型，然后介绍了改进的损失函数.第4节是实验参数配置和结果分析部分.最后，第5节是本文的结论.

2 相关工作

2.1 深度神经网络和残差学习

由于深度神经网络具有灵活的网络结构和强大的学习能力，因此深度学习技术目前已经成为解决图像降噪问题非常有效的方法.在这些方法中，Kokkinos[11]将级联网络运用到DCNN中，在图像降噪方面取得了较好的效果；在[12-13]中，在DCNN的基础上，引入了新的网络结构，分别利用信号增强原理和多特征融合方法多次复用各个隐藏层的特征信息，将其运用到图像降噪中，也取得较好的效果；还有学者运用特定的方法为特定领域噪声降噪，如[14-17]文献中采用的方法在乘性噪声、医学图像噪声的降噪方面取得显著成效等等.尽管上述的深度学习方法在图像降噪任务方面取得了很好的效果，但是当网络结构很深时，这些方法中的大多数会出现梯度消失或者梯度爆炸的问题，使网络性能退化.此外，上述方法是通过牺牲时间成本来提高降噪性能.

残差网络假设引用残差映射比原始未引用映射更容易学习，在图像处理过程中，它去掉相同的图像内容，从而更关注噪声部分.由于采用了残差学习策略，极深的CNN可以很容易地进行训练，提高了图像分类和目标检测的准确性[18].与残差网络不同，DnCNN使用单个残差单元来预测残差图像，并解决了多个图像降噪任务[4].为了提升训练效果，DnCNN将批量归一化和残差学习结合使用.

本文提出的DnDNN模型也采用了残差学习方法.与DnCNN不同，DnDNN方法使用反卷积在不同网络层次中对图像进行了重构，使得恢复的图像含有更少的噪声.与DnCNN相比，该模型具有收敛时间短、训练稳定、降噪性能好等优点.

2.2 反卷积

卷积网络是一种自底向上的方法，对输入图像进行多层卷积、非线性操作以及子采样.反卷积网络中的每一层都是自顶向下的，它试图通过对带有学习过滤器的特征映射的卷积求和来生成输入图像.反卷积网络利用卷积稀疏编码的多个交替层对图像进行分层分解.对第l层特征图像进行反卷积，得到第l层重构图像.如图1所示.

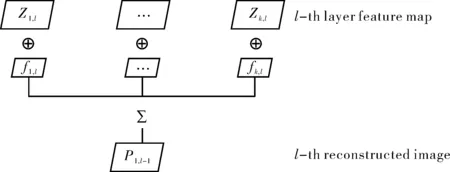
图1 反卷积过程Fig.1 Deconvolutional process

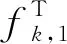
(1)

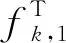
(2)

卷积神经网络可以看作是一个编码的网络结构[20]，提供从输入到潜在特征空间的自下而上映射；反卷积网络可以视为一个解码器，将潜在特征映射回原始图像空间.反卷积网络最初被认为是稀疏的、过于完整的特征层次结构，这与深度学习方法密切相关.反卷积网络可以学习从低层边缘到高层对象部分的图像表示，它以一种无监督的方式在不同的尺度空间上恢复图像特征.换句话说，深度学习对图像进行训练时，模型的不同层次学习到不同级别的图像特征信息.反卷积网络通过训练卷积核产生不同层次的基于卷积稀疏编码的潜在图像特征.DnDNN的反卷积结构采用了的层次模型，每一个反卷积层都试图在一组超完整特征图上进行稀疏约束，从而降低输入图像的重构误差.对于图像去噪，残差图像被视为DnDNN模型中噪声观测图像与重建图像的差值.

3 DnDNN去噪方法

一般来说，针对特定任务训练深度卷积神经网络模型分为两个步骤：1)设计网络结构；2)从训练数据中学习模型.在网络结构设计中，为了使其更适于图像降噪，本文在DnCNN的基础上，引入反卷积，并对原有的损失函数进行改进.

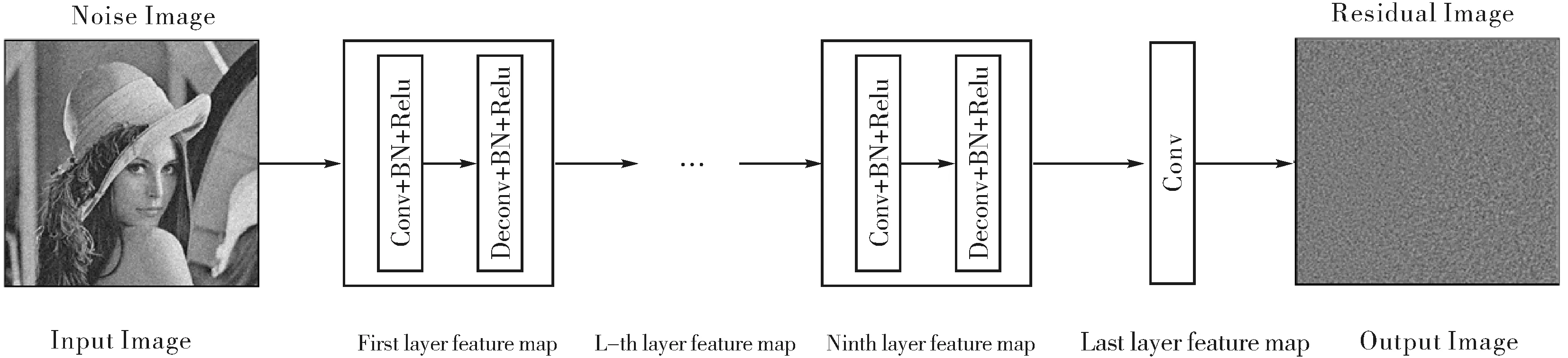
图2 DnDNN网络结构Fig.2 DnDNN network structure

3.1 本文提出的DnDNN结构

本文设计的网络结构如图2所示，设计的网络深度为10.每一层包含一组卷积运算和一组反卷积运算，卷积运算是用于提取图像的特征信息，包括边缘、线条等特征，反卷积运算是复原图像，反卷积在重构过程中，去掉了部分不能被重构的噪声信息；最后一层为全连接层，由一组卷积运算组成，用于输出图像.在上述结构中，每做一次卷积运算(或反卷积运算)后，紧接着做批归一化(Batch Normalization，BN)和RELU，以加快收敛速度，提升训练效果.

算法步骤如下：

1) 加噪的原始图像经过卷积计算得到特征图，然后对特征图进行反卷积，得到重构图像；

2) 加噪的原始图像减去重构图像得到残差图像；

3) 将原始噪声图像与对应的标签图像相减的结果，再与第2步的残差图像做差值，并进行最小化计算；

4) 设置迭代次数，当达到迭代次数时，训练停止，否则重复1)～3).

本文实验设置的图片块大小为30×30，步长为6，每层设置64个大小为3×3的卷积核，为了保证图片输入输出尺寸大小一样，采用零填充方式.除最后的全连接层外，每层处理包括卷积和反卷积，不使用池化层.

3.2 本文提出的损失函数计算方法

训练数据是带有噪声的图像y=x+v，通过学习训练数据的模式来寻找映射函数f(y)=x，目的是预测潜在的干净图像.本文采用残差学习获取映射R(y)≈v，然后得到x=y-R(y)，故损失函数的计算公式如下：

(3)

式中，yi-xi为样本残差值(即噪声图像值减去干净图像值)，R(yi;Θ)为通过学习得到的期望残差值，l(Θ)用L2正则化得到每个patch块的损失函数值.在DnCNN中，最终的损失函数是每个patch块损失函数累加，然后通过优化得到尽可能小的损失函数.由于均方误差函数(MSE)对梯度变化较为敏感，损失函数在收敛过程中鲁棒性较差，收敛速度较为缓慢.

为了缩短模型的收敛时间，又保证模型的降噪效果，本文结合L1正则化和L2正则化的各自优势，对上述损失函数进行优化，其公式如下：

(4)

式中，t为超参数，它用来调节损失函数L(t)的梯度.相比于平方损失，上式对于异常值不敏感，但它同样保持了可微的特性.它基于绝对误差(MAE)但在误差很小的时候变成了MSE.可以使用超参数t来调节的梯度，当t趋向于0时它就退化成了MAE，而当t趋向于无穷时则退化为了MSE.损失函数利用了MAE和MSE各自优点，不仅可以保持其具有连续的导数，同时可以利用MSE梯度随误差减小的特性来得到更精确的最小值，也对异常值具有更好的鲁棒性.通过实验分析，当把t的值设置为0.25时，既可以保证训练速度，也能较好的加快收敛速度.

4 实验结果和分析

对于已知或未知噪声水平的高斯降噪，训练集为400张像素为180×180的灰度图片.本文方法是在σ∈[0，55]噪声水平的训练集下进行训练的.为了验证本文方法对已知噪声水平的降噪效果，选取了噪声强度分别为σ=15、25、50的高斯噪声图像.每个patch块的尺寸大小为30×30像素.为了扩充数据样本，并且减小边缘效应的影响，将400张像素为180×180图片中的每张图片按照其尺寸大小的(1，0.9)倍进行2次裁剪，然后采用比DnCNN更小的步长，以便保留图片更多的边缘信息.为了验证本文方法的降噪效果，采用BSD68和SET12数据集进行测试.

4.1 参数设置和网络训练

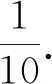
表1 BSD68数据集上不同方法的平均PSNR(DB)结果Tab.1 The average PSNR(db) results of different methods on the BSD68 dataset

表2 SET12数据集上不同方法的平均PSNR(DB)结果Tab.2 The average PSNR(DB) results of different methods on the SET12 dataset

表3 不同降噪方法在噪声级别为25，图像尺寸大小分别为256×256、512×512和1024×1024下分别在CPU和GPU下 运行时间(s)，对于CSF、TNRD、DnCNN和本文提出的DnDNN的CPU(左)和GPU(右)的运行时间Tab.3 Run time (in Seconds) on CPU (left) and GPU (right) of different methods on images of Size 256×256， 512×512 and 1024×1024 with Noise Level 25 for CSF，TNRD ，DnCNN and DnCNN

图4描述的是本文的DnDNN在基于梯度优化算法SGD，运用残差学习方法以及改进的损失函数在噪声强度为σ=25时模型训练的PSNR值随迭代周期的变化图.从图4可以看出，利用DnDNN方法训练时，当迭代周期到18次左右时，PSNR值趋近于稳定，为30.38 dB，其收敛速度非常快，训练效果也非常好.

图3 利用不同降噪方法得到的一张来自BSD68的噪声水平为50的图片的降噪结果Fig.3 The noise reduction result of a picture with a noise level of 50 from BSD68 obtained by different noise reduction methods

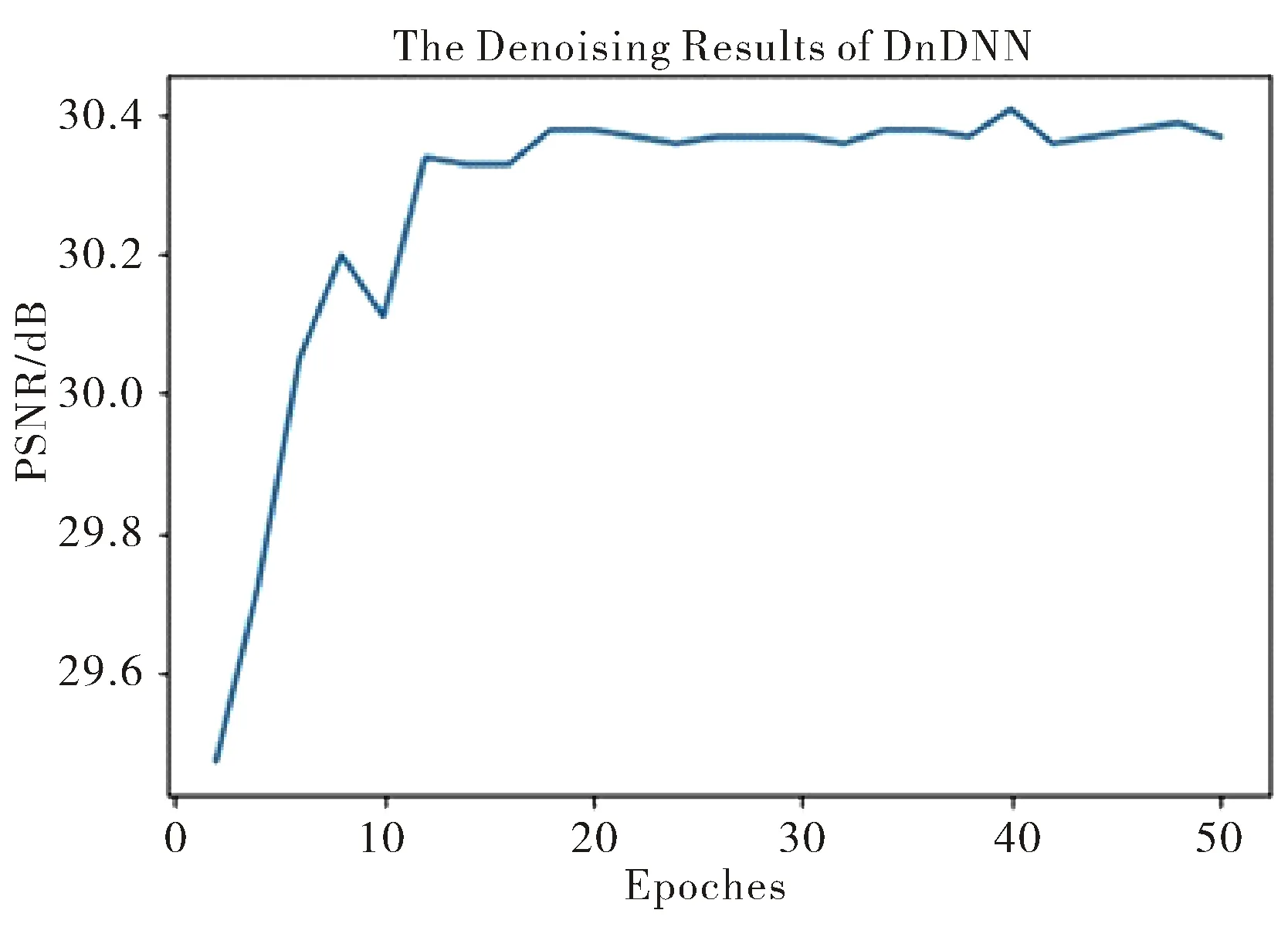
图4 DnDNN模型下σ=25高斯降噪训练收敛效果图Fig.4 Training convergence effect diagram of σ=25 Gauss noise reduction under DnDNN model

4.2 运行时间

除了降噪效果以外，模型的运行效率和收敛时间也是评价模型性能好坏的重要指标.表3给出了一些经典图像降噪算法在噪声级别为25，图像尺寸大小分别为256×256、512×512和1024×1024下运行时间，从表中数据可知，DnDNN方法的运行效率BMD和TNRD方法稍低，与DnCNN-B方法相当，考虑到DnDNN方法具有盲降噪的优点，本文提出的DnDNN方法仍然具有较高的计算效率.再考虑模型的收敛时间，由于DnDNN方法具有盲降噪性能，所以在对比模型的收敛时间时，DnDNN方法主要与DnCNN-B方法进行对比.从图5可以看出，当迭代20个周期时，本文提出的DnDNN算法训练结果趋于稳定，此时的PSNR值为30.38 dB.本文提出的方法每一个迭代周期所用的时间为317 s，略高于DnCNN-B每一个迭代周期所用的时间(DnCNN-B每一个迭代周期用时301 s).但是本文方法的收敛时间要远远少于DnCNN-B的收敛时间，DnCNN-B大约迭代50次才趋近于收敛，收敛时间大约为14 932 s，DnDNN的收敛时间仅仅约为6 263 s.对大量图像进行统计分析，本文方法收敛时间比DnCNN-B缩短了120%～138%.

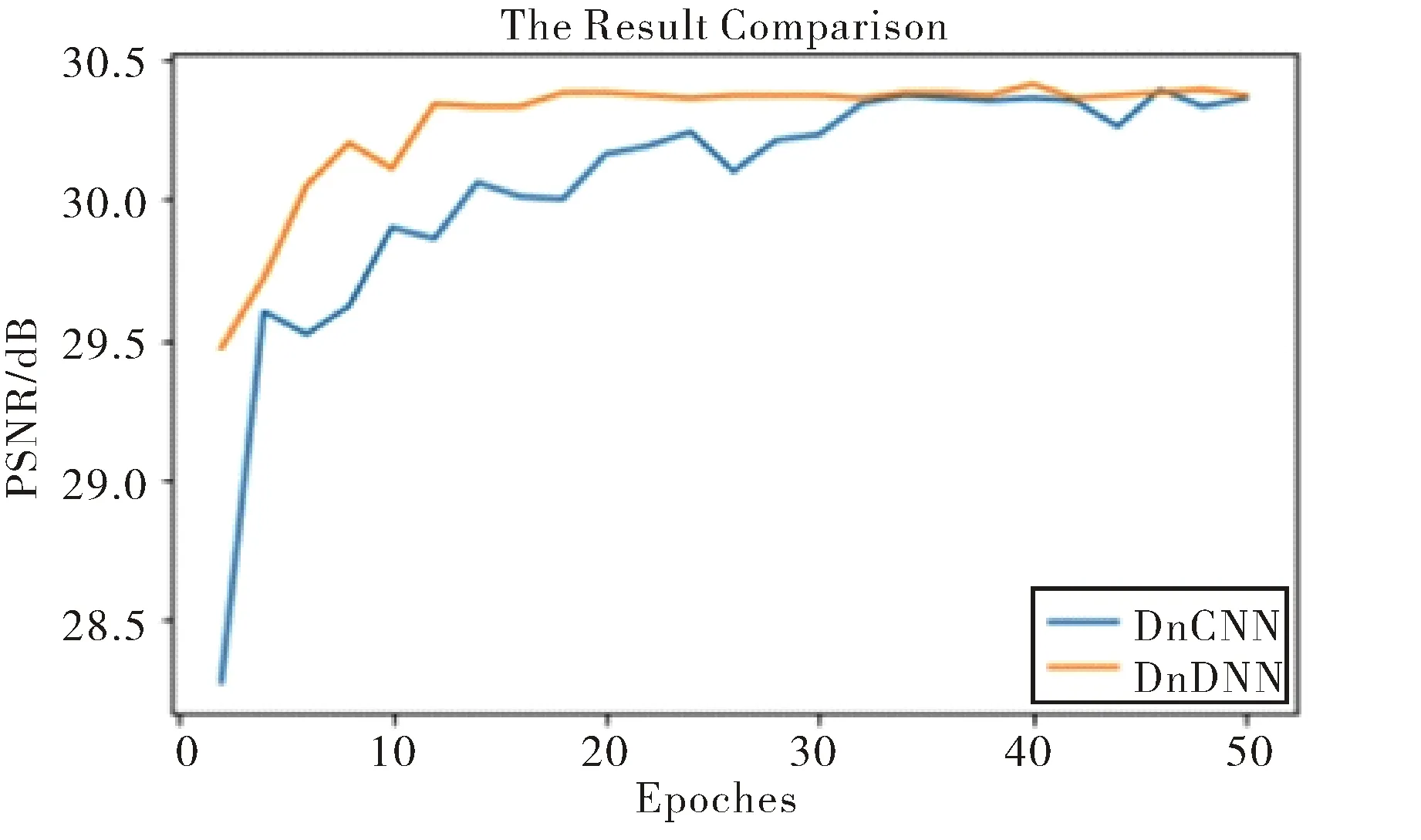
图5 DnCNN和DnDNN模型下 σ=25高斯降噪训练收敛速度对比图Fig.5 Comparison chart of convergence rate of σ=25 Gauss noise reduction training under DnCNN and DnDNN models

4.3 实验分析

为了比较本文方法与DnCNN-B方法之间的图像降噪效果，本文通过多组实验来分析影响训练收敛速度的因素.与收敛速度相关的网络参数包括学习率、batch块、步长、卷积层数以及损失函数.

图6 几种不同去噪方法在σ=25下的 高斯降噪训练收敛速度对比图Fig.6 Comparison of convergence rate of Gaussian noise reduction training under σ=25 for several different denoising methods

通过对影响训练收敛速度的因素分别设置不同数值，本文分别对图像去噪进行了5组实验，其结果如图6所示.

第1组实验是DnCNN-B的方法，它使用L2正则化作为损失函数，batch大小为40×40，步长为10，初始学习率为0.001，卷积层数为17.当迭代30次后，学习率减小为原来的1/10.

第2组实验与第四组实验的网络结构与DnCNN-B相同，只是对其参数设置进行了调整；第三组实验是在DnCNN-B方法的基础上在每个卷积层后面设置一个反卷积层，其余结构与DnCNN-B相同，具体设置如下所示：

第2组实验为 Test 1方法，设置batch大小为40×40，步长为10，初始学习率为0.001，卷积层数为17.当每迭代10次后，学习率减小为原来的1/10.

第3组实验为 Test 2方法，使用L2正则化作为损失函数，设置batch大小为30×30，步长为6，初始学习率为0.001，卷积和反卷积结层数为10，当每迭代10次后，学习率减小为原来的1/10.

第4组实验为 Test 3方法，使用L2正则化作为损失函数，设置batch大小为30×30，步长为6，初始学习率为0.001，卷积层数为17.当迭代30次后，学习率减小为原来的1/10；

第5组实验是本文提出的 DnDNN方法.在网络结构中加入改进的损失函数和反卷积层的基础上，设置batch大小为30×30，步长为6，初始学习率为0.001，层数为10.当每迭代10次后，学习率减小为原来的1/10.

从图6可知，在5组实验中，DnDNN降噪方法获得了最好的去噪效果，当迭代20个周期时已经趋于稳定.本文方法与DnCNN-B方法比较，其训练收敛速度提高的主要贡献为在原有的网络结构中加入反卷积层，且应用改进后的损失函数计算图像的残差值.

5 结论

本文在原有的深度残差学习的网络结构中，通过引入反卷积层和改进损失函数，提出了一种基于反卷积降噪神经网络的图像降噪算法.反卷积的引入提高了噪声图像残差学习的质量和效率，对损失函数的优化，则进一步加快训练收敛速度，提高降噪效果.与针对特定图像噪声水平训练得到的判别模型不同，本文提出的DnDNN算法具有较强的处理未知噪声水平的能力.与DnCNN-B算法相比，在保证降噪效果和运行效率的情形下，本文算法的收敛时间大幅降低.