基于经验似然修正的艾滋病药物疗效对比分析研究

何孟霜，夏文俊，孙静茹，来 鹏

(南京信息工程大学数学与统计学院，南京 210044)

ACTG175是一个比较治疗艾滋病药物zidovudine(齐多呋定)或didanosine(去羟肌苷)的单药治疗，与zidovudine和didanosine的联合治疗或zidovudine和zalcitabine(扎西他宾)的联合治疗的随机临床试验.1995年研究的初步结果表示，ACTG175和CPCRA007被NIAID首次宣布已经在定义治疗艾滋病感染者的标准和塑造后续临床研究抗逆转录病毒药物方面发挥了重要作用[1].

HIV病毒对人体有CD4+受体的淋巴细胞，主要是CD4+T淋巴细胞进行攻击，它同时也会侵袭神经细胞.HIV病毒对人体细胞的感染有两大特点：变异和潜伏.这也是感染艾滋病后的潜伏期比较长以及艾滋病疫苗很难研制成功的最大原因.CD4+细胞是人体免疫系统中的一种重要免疫细胞，其数量体现了药物对HIV的抑制效果[2].CD4+计数的升高是由于药物有效抑制了病毒复制，机体有机会产生新的未被病毒感染的CD4+细胞，从而增强人的免疫系统并减少各种机会性感染，所以其检测结果对艾滋病治疗效果和对患者免疫功能的判断有重要作用.

在流行病学文献中，平均治疗效果是评估治疗效果并被广泛接受的一种方法.但是需要注意的是，疗效平均值的估计会受到分布的有偏性、重尾或异常值等的影响，有可能导致疗效判定的误判.所以，更稳健的基于中位数的平均治疗效果评判方法是迫切需要的.此外，在药物临床试验中，由于试验对象只能包含在一个测试组内，这导致该对象的其他测试组数据是缺失的，所以药物临床试验数据本身是一个缺失数据问题.对该信息的有效利用，有助于提高药效对比分析的准确性.Firpo[3]利用Nadaraya-Watson核估计得到倾向得分函数，通过Horvitz-Thompson逆概率加权方法研究了基于中位数的治疗效果对比.更进一步的，Wang和Lai[4]提出了一种利用经验似然技术[5]对设定的参数工作模型进行改进的方法，能够有效计算药物疗效的中位数差.考虑到方法的灵活有效性，本文引入该方法到药物疗效评价的研究中.为此，本文针对ACTG175的艾滋病药物临床试验数据，在治疗对象相对数据缺失的情况下使用经验似然方法及中位数差对其进行疗效对比研究，以期给出切实可行、有效的药物疗效对比分析方法，并可广泛应用于药品疗效分析中.

1 临床试验资料

ACTG175数据主要包含下列解释变量：age(年龄)、wtkg(体重千克)、hemo(血友病，0=无，1=有)、homo(同性恋活动，0=无，1=有)、drugs(药物静脉注射毒品史，0=无，1=有)、karnof(卡氏评分0～100)、oprior(开始研究治疗前无zidovudine抗逆转录病毒疗法，0=否，1=是)、z30(治疗开始前30天使用zidovudine，0=否，1=是)、zprior(治疗开始前使用zidovudine，0=否，1=是)、preanti(之前接受了抗逆转录病毒治疗的天数)、race(种族，0=白人，1=非白人)、gender(性别，0=女，1=男)、str2(抗逆转录病毒治疗历史，0=无，1=有)、strat1(抗逆转录病毒治疗历史，1=是“未经过抗逆转录病毒疗法”，0=否)、strat2(1=是“经过2到52周的抗逆转录病毒疗法”，0=否)、symptom(症状指标，0=无症状，1=有症状)、treat(治疗指标，0=zidovudine，1=其他疗法)、offtrt(退出治疗在96±5周，0=否，1=是)、r(CD4+T细胞在96±5周的计数是否缺失，0=失踪，1=有观察)、days(直到第一次出现病症的天数)：1) CD4+T细胞的数目至少下降50，2)事件显示为艾滋病，或者(3)死亡).为了方便后续计算，分别将上述变量定义为(x1，x2，…，x19，x20).

ACTG175数据中四种药物治疗方案分别是：arms=0为zidovudine单独用药，arms=1为zidovudine和didanosine联合用药，arms=2为zidovudine和zalcitabine联合用药，arms=3为didanosine单独用药.本文通过研究在arms=0、1、2、3这四种不同的药物治疗方案下，经过20周后CD4+T细胞的数量差异来观察这四类不同的药物治疗方案是否显著不同.

2 药物疗效比较方法

2.1 参数模型下的中位数回归法

为了比较药物疗效，以arms=0和arms=1这两种方案的比较为例，设Y0i和Y1i分别表示arms=0和arms=1时的第i个病人在第20周时的CD4+T细胞数目，Y1i-Y0i即为方案1和方案0的疗效差异.但是由于病人只存在这两种方案之一的情况，接受其中一种用药方案时，另外一种用药方案的情况则是缺失的，因此令δi表示病人所在分组情况：

整个数据集可分为arms=0和1两种情况.观察到的数据集可表示为(Yi，Xi，δi)，i=1，2，…，N，其中Yi=δiY1i+(1-δi)Y0i，Xi=(x1i，…，x20i)T表示第i个观测向量.

对于传统的基于均值差来反映药效疗效的方法，可以通过已知的(Y1i，Xi)和(Y0i，Xi)来计算.记不同药物下随机向量的联合分布分别为F1(y，x)和F0(y，x)，那么Y1i和Y0i的边缘分布分别为F1(y)和F0(y)，显然疗效期望差表示为：

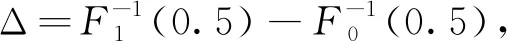
考虑到自变量过多，而过多的自变量容易导致拟合模型产生冗余信息，变量间也可能出现强相关关系.因此，本文通过研究因变量与自变量之间的相互影响，应用逐步回归检验方法筛选出不同药物治疗方案下的重要变量，即原始多元线性回归模型：

y=β0+β1x1+β2x2+…+β20x20+ε，

利用逐步筛选得到的重要变量构建多元线性回归模型：

ψ(x，β，t)=F1(t|x，β)-1/2，

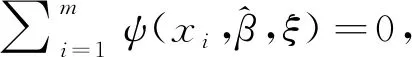
2.2 逆概率加权下的中位数回归法

逆概率加权方法最早是由Horvitz和Thompson[6]提出，通过对观测的yi进行加权，从而改进建模效果.arms=0和1两种方案表明在观察其中一种用药方案时，另外一种用药方案的情况是缺失状态，即20周的CD4+T细胞数据缺失.不妨设这种缺失是随机缺失，也就是

P(δ=1|Y1，Y0，X)=P(δ=1|X)=ω(X，θ)．

(1)

2.3 经验似然修正的中位数回归

前面所给出参数模型中假设了正态分布模型作为工作模型进行计算，但该假设的正确性需要对四种用药方案下20周的CD4+T数目进行正态性检验.如果拒绝正态性假设，则无论是在F1还是F0的工作模型下，上述采用的基于参数模型的中位数回归比较的结果都会有较大偏差，而逆概率加权法，从公式(1)可以发现利用到的X的信息不充分.

本文将采用经验似然方法对条件正态分布F1和F0下的结果进行修正，通过对缺失概率和伪似然函数的模型改进，获取更多信息，来确定不同方案的中位数.Owen[7-8]首次系统地提出了经验似然法，并用来处理非参数统计问题.经验似然方法作为一种非参数统计方法有很多优点，除置信区间的域保持性、变换不变性及由数据决定置信域的形状外，还有Bartlett纠偏性及无需构造枢轴统计量等优点[9].

已知(y1i，xi)，i=1，2，…，m和(y0i，xi)，i=1，2，…，n，定义如下的伪似然函数：

其中，F1(y1i，xi)和F0(y0i，xi)具有共同的边缘分布F(x)，则arms=1时第i个个体的抽取概率为pi=dF1(y1i，xi)，i=1，2，…，m，而arms=0时第i个个体的抽取概率为qi=dF0(y0i，xi)，i=1，2，…，n.由E(ω(X，θ)-η)=0，E[ψ(X，β，ξ)]=0，η=E[ω(X)]=p(δ=1)，可构建带约束的对数似然函数为：

(2)

其中，pi，qi满足以下条件：

为求对数似然函数的最大值，引进拉格朗日乘子λ1，λ2，τ1，τ2，得到：

(3)

其中，λ1,λ2,τ1,τ2满足下面四式:

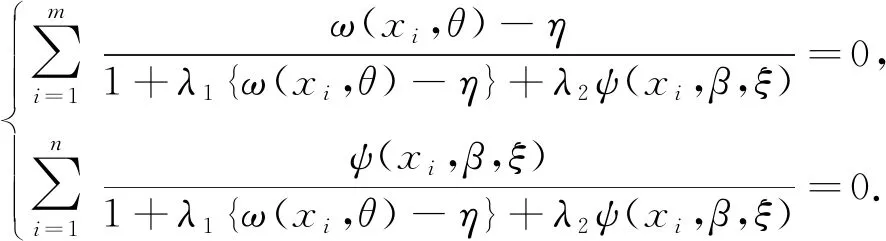
将λ1,λ2,τ1,τ2的估计值代入(3)式，可求得针对arms=1中每个个体的缺失率pi，i=1，2，…，m和针对arms=0中每个个体的缺失率qi，i=1，2，…，n.则经验似然调整后的两个分布下的中位数，可通过求解下列方程组得到：

(4)

3 不同方法下的结果比较

在参数模型下，假设20周的CD4+T细胞数目服从条件正态分布，通过逐步回归检验方法筛选出不同药物治疗方案下与目标变量具有较大联系的自变量.筛选结果显示F1的均值和x11，x12，x13，x16，x20相关，F0的均值和x13，x16，x20相关，即条件分布函数为：

F1(y|X，β)～N(β1+β2x11+β3x12+

β4x13+β5x16+β6x20，1)，

F0(y|X，γ)～N(γ1+γ2x13+γ3x16+γ4x20，1)，

其中F1，F0分别代表arms=1和arms=0时20周的CD4+T细胞数目的分布函数，β1，…，β6和γ1，…，γ4为未知参数.由极大似然估计法，可得arms=1和0两种方案中的20周的CD4+T细胞数目服从的正态条件分布函数如下：

F1(y|X，β)～N(335.009-44.87x11->35.2x12-80.107x13-46.067x16+0.18x20，1)，F0(y|X，γ)～N(243.122- 53.453x13-40.145x16+0.163x20，1)．

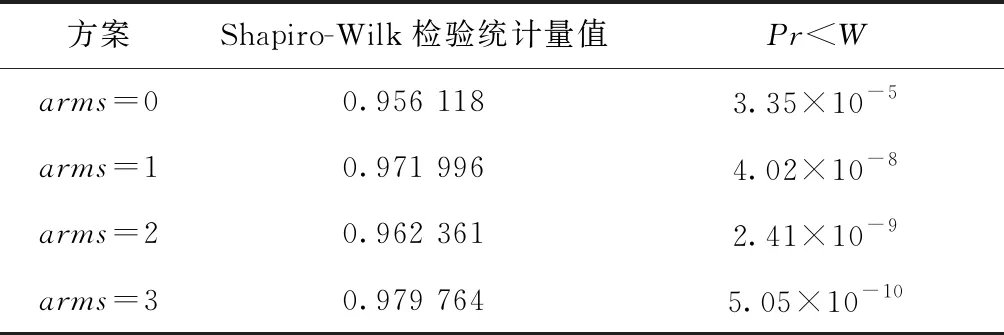
表1 四种方案的正态性检验结果Tab.1 Normality test results of four schemes

然而，对四种方案下20周的CD4+T细胞数目进行正态性检验(表1)，可以看出各方案下的Shapiro-Wilk检验统计量的值均接近1，p值显著小于0.05，表明四种方案都拒绝了正态性的原假设，即不服从正态分布.故考虑引入逆概率加权及经验似然的中位数回归模型调整分布，结合式(1)、(3)、(4)计算不同方案的中位数差，将所求中位数两两组合进行比较，结果见表2.

从表2可以看出，样本中位差、逆概率加权和经验似然等方法估计中位数之差时发现，arms=0时20周的CD4+T细胞数目明显少于其它3种方案，arms=1时20周的CD4+T细胞数目多于arms=2和3，arms=2和3之间20周的CD4+T细胞数目几乎没有差异.可以初步判断，arms=1的疗效优于其它3种方案，arms=0的疗效劣于arms=2和3，arms=2和3的疗效几乎没有差异.而在基于参数模型的中位数回归比较时观测到的疗效差异和其它方法相比差距较大，尤其体现在arms=3和1的比较中，该方法所得结果arms=3的疗效要优于arms=1的疗效，与另外三种比较方法结果相反，其它比较结果同另外三种比较方法类似.由于比较中位数之差没有利用协变量的信息，参数模型的中位数回归基于很强的正态分布假设，逆概率加权方法未利用全部信息，而经验似然估计修正了这三种比较方法的缺陷，其结果最贴近真实情况，即arms=1的疗效优于其它3种方案，arms=0的疗效劣于arms=2和3，arms=2和3的疗效几乎没有差异.为了对这种差异的显著性进行验证，本文采用Bootstrap来估计中位数之差的置信区间并进行检验判断.

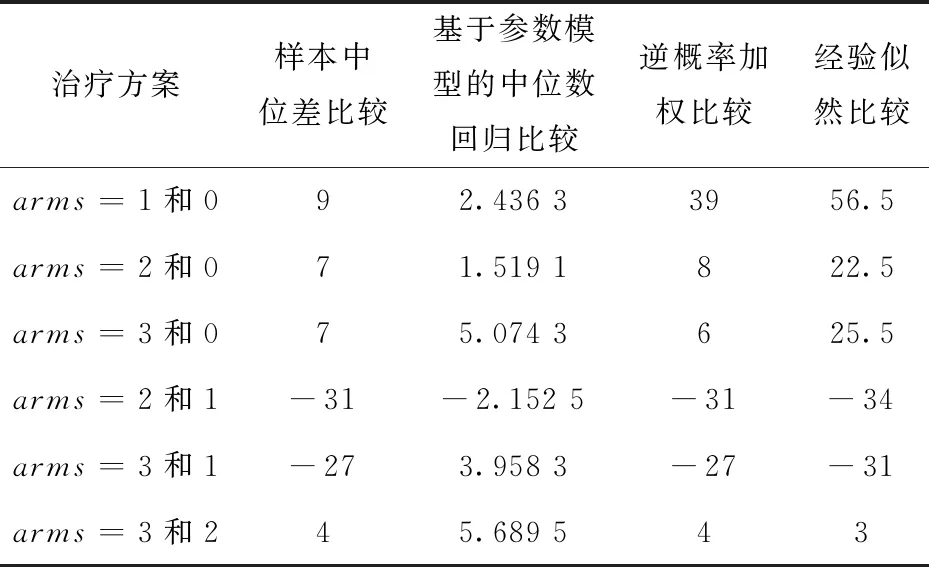
表2 四种比较方法下疗效中位数差异的综合结果Tab.2 The comprehensive results of the difference in the median efficacy of the four comparison methods

Bootstrap是非参数统计中一种重要的估计统计量方差进而进行区间估计的统计方法，也称为自助法[10].取显著性水平为0.05，得到4个用药方案抗艾滋的疗效差异对比的置信区间见表3.

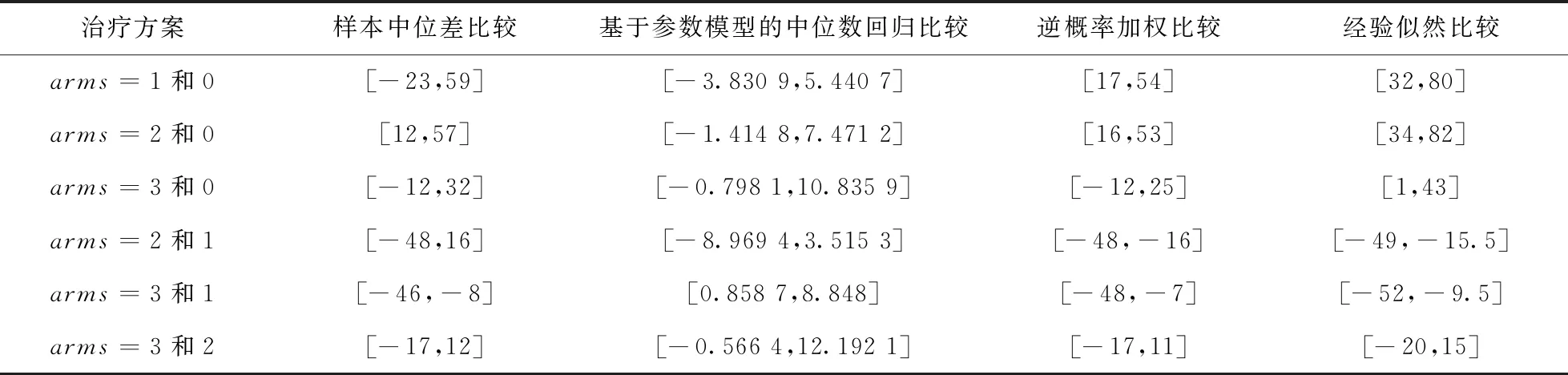
表3 中位数之差的置信区间Tab.3 Confidence interval for the difference between the medians

表3给出了在四种中位数比较方法下，对arms=0、1、2、3这几种治疗方案相互比较的结果，显著性水平取0.05.纵向观察经验似然法下两两比较的结果，发现arms=0和arms=1、2、3中20周的CD4+T细胞数目的中位数之差的置信区间都在零点右侧，说明arms=0时20周的CD4+T细胞数目显著小于其它3种方案20周的CD4+T细胞数目，表明zidovudine单独用药的抗艾滋效果显著最差.而arms=2、3和arms=1时20周的CD4+T细胞数目的中位数相比，20周的CD4+T细胞数目的中位数之差的置信区间都在零点左侧，因此认为arms=1时20周的CD4+T细胞数目显著大于arms=2、3时20周的CD4+T细胞数目，表明zidovudine和didanosine联合用药的抗艾滋效果要显著优于zidovudine、zalcitabine联合用药和didanosine单独用药的效果.而arms=2和3中位数差的置信区间包含零值且关于零值几乎对称，因此认为zidovudine与zalcitabine联合用药和didanosine单独用药的抗艾滋效果没有显著差别.综上，arms=1即zidovudine和didanosine联合用药能有效提高20周的CD4+T细胞数量，从而抑制病毒复制，表现出较好的的抗艾滋疗效.

通过观察表3，比较arms=1和3、arms=2和3这两组的中位数之差时，基于参数模型的中位数回归比较法的置信区间相较其它几种比较方法，结果粗糙且可信度低，而经验似然方法下的置信区间与其它几种方法的置信区间相比差异更显著且可信度更高.

4 结论

本文根据ACTG 175的数据分析不同用药方案下的抗艾滋疗效差异.基于参数模型的中位数回归建立在正态分布模型假设之下，计算简便快速，但是由于假设条件过强，导致结果偏差较大.为此采用经验似然调整分布，根据缺失数据的特点，定义伪似然函数并引进拉格朗日乘子，结合极大似然法求解出中位数之差.最后利用Bootstrap抽样方法得到置信区间以观察各组方案的疗效差异.对结果分析，得到结论：zidovudine和didanosine联合用药的抗艾滋效果显著最优，zidovudine单独用药的抗艾滋效果要显著劣于zidovudine、zalcitabine联合用药和didanosine单独用药，zidovudine和zalcitabine联合用药和didanosine单独用药的抗艾滋效果没有显著差别，zidovudine单独用药的抗艾滋效果显著最差.