基于SEIR模型的中国山东省与韩国COVID-19疫情早期传播特征比较分析

邵俊杰，禹世雄，高婧婧，袁 鸣，吕 中，江 南

(武汉工程大学环境生态与生物工程学院，武汉 430205)

由新型冠状病毒(SARS-CoV-2)引发的肺炎疫情(COVID-19)，不仅发病症状与严重急性呼吸综合征(Severe Acute Respiratory Syndrome，SARS)类似，还呈现了SARS所不具备的高度传染性[1].截至2020年8月10日，COVID-19已然传播至世界大部分国家和地区，给全体人类带来了接近20 000 000例确诊和超过720 000例死亡.为此，由我国政府首倡，世界多国政府采用了关闭学校、餐厅等多个公共场合的管控措施[2].与之同时，多种数据模型被建立并用于预测、分析上述因素对COVID-19传播的影响[3-7].由于世界地域的复杂性，人口密度、气候条件等诸多因素会对病毒传播产生影响，但目前的预测模型很少涉及.

有鉴于此，本文通过对气温、湿度、人口密度等因素进行考察，选取了韩国和中国山东省这两个样本用于比较；使用经典SEIR仓室模型[8]对COVID-19在两地的传播动力学特征进行回溯分析，以验证物理性疏离和保持医疗资源高效运作对阻断COVID-19传播的重要意义.

1 研究对象选择与回溯模型构建

1.1 样品选择

现有针对COVID-19传播动力学展开的建模研究涵盖了统计学模型、时空传播模型、小世界网络等多个方面，但多局限于预测COVID-19的传播趋势，未能对已发生疫情的区域的防控、救治措施有效与否做出分析.据已有报道，基于微分方程的数学模型反而多被用于开展以上措施有效性的回溯分析，其中又以SEIR模型最为常见，如吴建宏等[9]建立SEIR模型用来模拟并分析湖北限行措施对北京疫情情况的影响，发现并报道了采取快速、有效公共卫生措施的重要性.另一方面，诸如温度、湿度等环境因素将有效影响病毒存活与传播途径[10-11]，而环境、人口密度、文化差异、人种差异等因素对于COVID-19传播的影响尚无定论.与之相对应，基于微分方程的数学模型无法对这些因素进行考量，需要引入更为复杂的时空序列分析[12].因此，通过环境等因素筛选研究的样本，可以使用简单、经典的SEIR仓室模型模拟COVID-19在我国部分地区与其他国家传播的情况，较为精准地分析我国和他国管控措施的有效性.

中国和韩国共处东亚，互为近邻而人员、物质交流往来频繁，并均受到了儒家文化圈的长期影响，是用于对比分析的极佳对象.但是，中国幅员辽阔，南北的地域差异等因素可能会影响SEIR模型的准确性，因此，本文选定了COVID-19在中国山东省的传播情况与在韩国的传播情况进行对比.这两个样本的相似性体现在：1) 均为外源性输入；2) 韩国与中国山东省地理条件相近，位于33°～38° N的半岛地带，均属于温带季风气候，山东省年平均气温11 ℃～14 ℃，韩国年平均气温13 ℃～14 ℃；3) 两地面积相似、人口密度相似，山东省面积约为15.8万km2，人口密度约为630人·km-2，韩国面积约为10万km2，人口密度约为514 人·km-2(以上结果分别来自中国政府网站最新公布的山东省省数据和世界银行集团The World Bank最新公布的韩国数据)；4) 同属儒家文化圈影响范围，主要人种均为亚洲人种.

1.2 数据来源

中国山东省病例数据来自中国卫生健康委员会官方网站(http://www.sdcdc.cn)2020年1月23日至4月26日的公布结果；韩国病例数据来自于韩国疾病预防控制中心(Korea Centers for Disease Control and Prevention，KCDC)网站(https://www.cdc.go.kr)2020年2月7日至4月27日的公布结果.上述病例原始数据经收集整理，即为本研究的COVID-19病例数据库.

1.3 SEIR模型构建

经典SEIR仓室模型将人群分为S(易感人群)、E(暴露人群)、I(感病人群)、R(康复人群).将SEIR模型用于COVID-19的疫情分析需作如下7条假设[8]：1) 治疗中的患者因隔离而不具感染能力；2) 不考虑无症状感染者；3) 不考虑二次染病者(现公布数据中无相关报道)；4) 与感染者接触但未被隔离的暴露人群与易感人群均匀混合；5) 不考虑人口出生率、死亡率以及迁入迁出的影响；6) 未将死亡患者与幸存患者分开，均视为确诊人群；7) 模型仅考虑人与人传播途径，未模拟其他可能的传播途径.

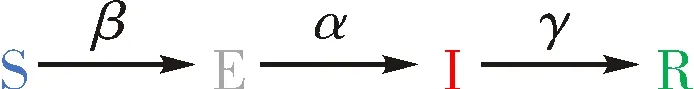
图1 COVID-19的SEIR模型
Fig.1 The SEIR model of COVID-19

β

α

γ

r

(1)

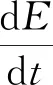
(2)

(3)

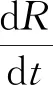
(4)

将(1)～(4)修改为迭代形式，如下所示

Sn=Sn-1-rβIn-1Sn-1/N，

(5)

En=En-1+rβIn-1Sn-1/N-αEn-1，

(6)

In=In-1+αEn-1-γIn-1，

(7)

Rn=Rn-1+γIn-1.

(8)

SEIR模型中E的数值在已公布数据库中缺乏记录，需近似估计.本文以潜伏期内现存确诊患者人数变化近似得到E，并将平均潜伏期定为符合多数报道的7 d[13-14](最后7 d数据不参与分析).基于以上假设，遂得中国山东省和韩国两个样本中E随时间变化图(图2).

图2 中国山东省(A)和韩国(B)的E值随时间变化图Fig.2 Temporal variation of E value of Shandong Province in China and South Korea

2 COVID-19在中国山东省和韩国的传播动力学差异

2.1 转化率

在SEIR模型中，α代表了暴露者向患病者的转换率，而这一数值通常由疾病自身性质决定[15].在中国山东省和韩国的数据中，COVID-19疫情的α相对稳定.以图3的E值与日期的关系可求解得对应的α值，但管控措施的采取可能对相应结果造成干扰.如山东省2月20日疫情便得到了基本的控制，因此在这几段时间内的α受随机因素影响拟合误差较大.通过舍弃波动较大的α值，得到中国山东省拟合范围在0.16～0.18，韩国拟合范围在0.16～0.19(图3).

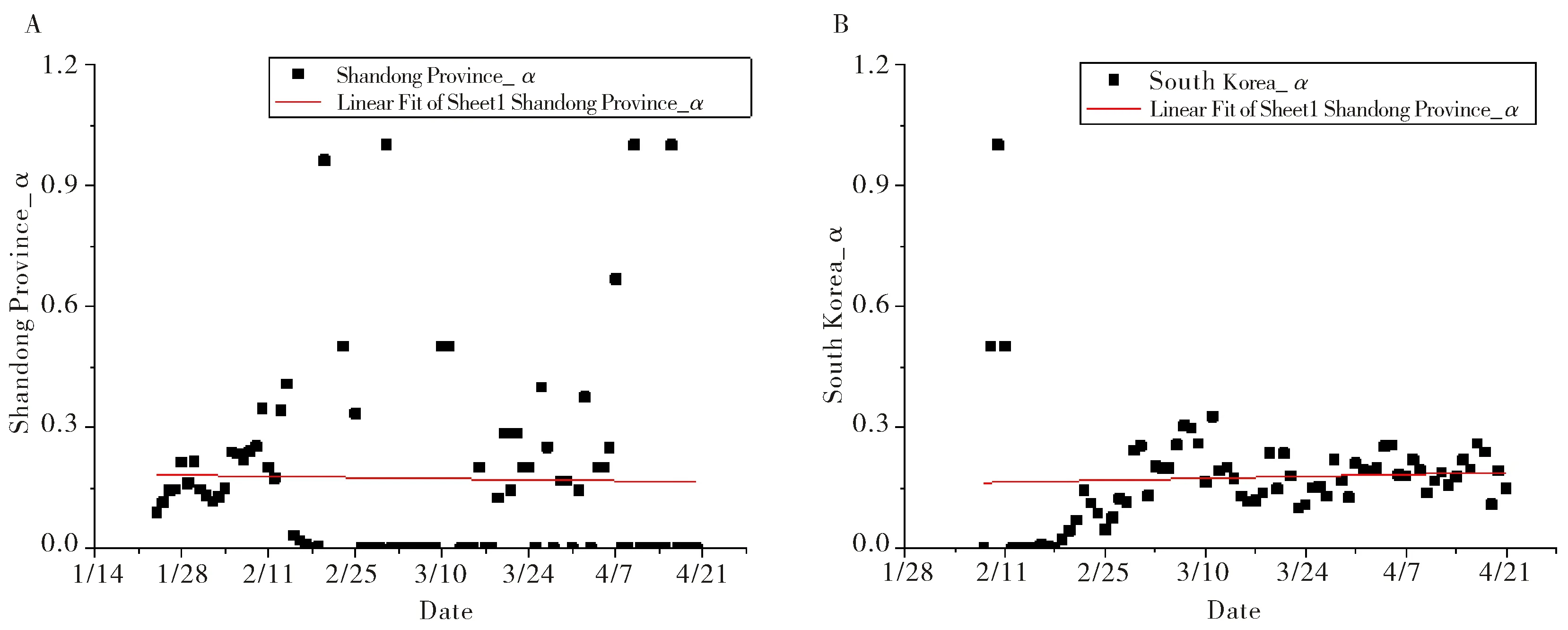
图3 中国山东省(A)和韩国(B)的α值随时间变化图Fig.3 Temporal variation of α value of Shandong Province in China and South Korea

2.2 患病者每日传染人数

降低E值是控制COVID-19传播速率的关键.由公式(2)推知，E与患病者每日感染人数(rβ)及α有关，而后者较为恒定.图4显示了两个样本中rβ与E随时间变化的趋势.在COVID-19疫情初期，两个样本中的E均伴随rβ的升高呈明显升高趋势；但中国山东省样本中的rβ并未随时间推移出现峰值，反而在2月18日降为0.与之相反，韩国样本中的rβ在2月17日达到峰值10.55，并于2月20号达到次高峰7.44.有鉴于此，韩国的E值最高达3 744(2月28日)，是中国山东省最高E值的1 717.43%(E=218，2月14日).

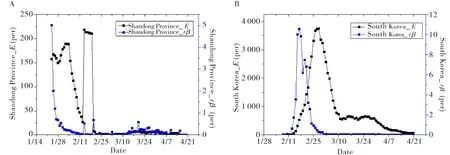
图4 中国山东省(A)和韩国(B)的rβ与E随时间变化图Fig.4 Temporal variation of rβ and E value of Shandong Province in China and South Korea

2.3 每日治愈率

患病者数量I由暴露人群数量E和康复者数量R共同决定，而后者与治愈率γ直接相关.图5显示了两个样本中I与γ随时间变化的趋势.在COVID-19爆发后，韩国的γ维持在较低水平，峰值仅达到了0.13(2月13日)，并迅速降低至0；从3月10日到4月21日，韩国的γ则处在0.011～0.079的范围内.与之相反，中国山东省的γ从早期开始一直处于上升趋势，于3月9日到达峰值0.53，是韩国γ峰值的410.23%.与之同时，中国山东省的I值在较短时间内达到峰值476(2月20日)，而韩国的I值到3月12日才到达峰值7 470，是中国山东省的1 569.33%.

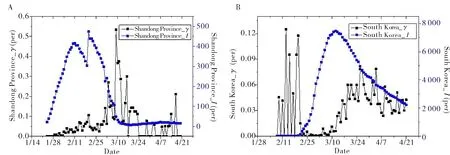
图5 中国山东省(A)和韩国(B)的I与γ随时间变化图Fig.5 Temporal variation of I and γ value of Shandong Province in China and South Korea

3 动力学差异的背后原因

中国山东省和韩国在环境等因素上高度相似，但COVID-19在两地的传播动力学特征却存在极大差异；这源自于它们不同的管控措施.表1列举了两地COVID-19的爆发时间点和他们首次发布的防控措施细则.一方面，中国山东省仅在首例确诊后5 d即发布相应通告，比韩国快29 d.另一方面，中国山东省的物理隔离策略和医疗救治也远比韩国更为严格、高效.本文现将这些管控措施与COVID-19传播动力学的关系归纳如表1所示.

表1 中国山东省、韩国的防控措施对比表Tab.1 The comparison table of prevention and control measures in Shandong Province in China and South Korea

3.1 更严格的物理疏离

每日感染人数与暴露人数直接相关，管控措施里面的物理疏离是降低暴露人群数量的有效方法.从发现首例确诊病例起，中国山东省、韩国rβ对比如图6A所示.中国山东省的措施十分及时，在发病5 d后就迅速开始了管控，因而rβ快速降到了0，并在之后的时间里面始终保持在接近0的范围内.韩国的rβ则因为没有管控措施，则在2月17日达到峰值10.55，但伴随2月23日管控措施的发布，rβ则出现了明显的下降.以上结果表明了物理疏离对降低rβ的有效性，且低于一个潜伏期(7 d)的反应速度可以很好地避免rβ高峰的出现.另一方面，中国山东省和韩国的E值均出现高峰，但韩国的E值峰值是中国山东省E值峰值的1 717.43%(图4A和4B).以上参数的显著性差异主要来自于两者采取物理性疏离措施的严格程度.相对于韩国的建议避免出门，中国山东省更加严格的物理阻断措施包括实行网络化防控、采取严格的出行限制.这些严格的物理阻断措施对于降低E和rβ的作用十分显著.

3.2 更高效的医疗救治

高效的医疗救治是提高γ的关键，可以有效地降低I并增加R的值.如图6B所示，自疫情发生后中国山东省的γ逐步升高，于3月9日到达峰值0.53；总耗费13 d，约为2个潜伏周期.反观韩国的γ，在政府开始征集特殊床位后的峰值反而低于了早期(2月13日)γ值(0.13).这一极不寻常的现象的原因是短期内大量增长的COVID-19患者挤兑了有限的医疗资源，大大降低了γ.一方面，韩国的E值远高于中国山东省，而α恒定，使得韩国的I值峰值是中国山东省的1 569.33%.另一方面，低水平的γ限制了由I向R的转变，造成了COVID-19患者的积压；并反过来又使得γ进一步降低.医疗资源丰富与国家发达程度一般呈正相关，因此作为发达国家的韩国在疫情初期有着较高的治愈率，但没有积极行使有效物理疏离，导致I值增长迅速，医疗资源被挤兑；之后虽然采取了调配床位、提高医疗用品供给等医疗调控手段，但并未专门针对COVID-19疫情设立独立的方舱医院，造成γ恢复缓慢，且始终维持在0.011～0.079的低水平.反观经济发展较慢的山东省，不仅及时通过物理疏离带来有效降低了E和I；还通过集中收治隔离，将轻症患者集中在方舱医院，有效缓解了医院床位紧缺的问题，并通过统一供给调控医疗物资，使医疗物资得到了更充分的利用.因此，山东省的γ在3月9日升至峰值0.53，是韩国γ峰值的410.23%.

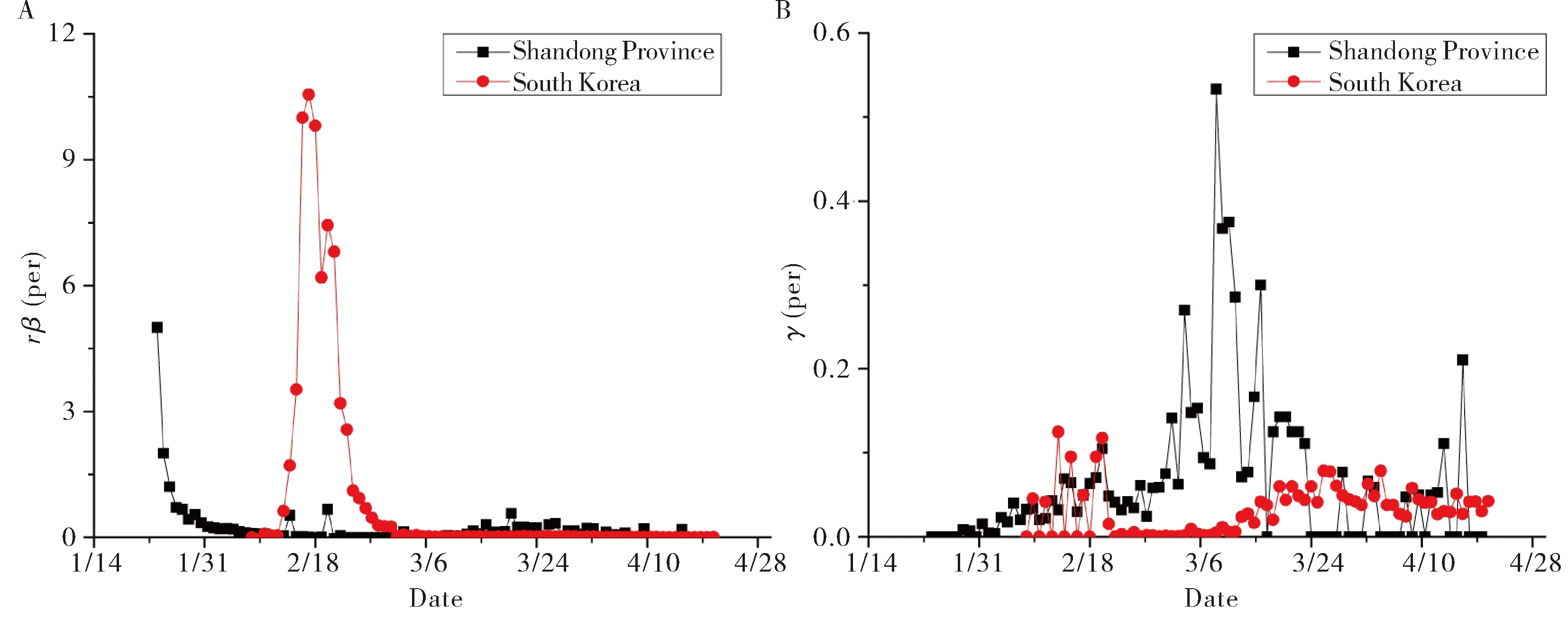
图6 中国山东省和韩国的rβ(A)和γ(B)随时间变化趋势的对比Fig.6 Comparisons of temporal variation of rβ (A) and γ(B) value of Shandong Province in China and South Korea

4 总结

通过基于SEIR模型的微分方程，本文对中国山东省与韩国这两个样本的COVID-19疫情进行了传播动力学特征的回溯分析.由于中国山东省与韩国在环境、人口密度、文化差异、人种差异等因素上的高度相似，本文避免了经典SEIR仓室模型不能兼顾时空、地域因素的弊端，充分对比了以上两个样本E、I、rβ、γ等动力学特征值的不同，并重点探讨了早期物理疏离、医疗救治效率对这些特征值的影响.一系列的证据显示，COVID-19疫情的阻断需要所在地政府迅速采取防控措施(短于一个潜伏期，7 d)，采取包括实行网络化防控在内的严格的物理疏离，以最大程度减少暴露人群数量.在此基础上，所在地政府还应向中国山东省学习，快速建立方舱医院，在避免医疗资源被COVID-19患者挤兑的基础上努力提高治愈率峰值，以实现确诊患者群向康复人群的快速转换.