永磁直驱式带式输送机系统动态特性及能耗分析
2020-12-29季晨光
胡 坤, 季晨光, 蒋 浩, 潘 泽
(1.深部煤矿采动响应与灾害防控国家重点实验室, 淮南 232001; 2.安徽理工大学机械工程学院, 淮南 232001)
带式输送机作为一种运输能力强、输送距离长的散料运输设备,被广泛应用于煤矿、冶金、交通等行业。目前,带式输送机常用的驱动系统有三类, 分别为液力耦合器驱动系统、液黏性调速器驱动系统和交流变频驱动系统[1-4]。上述驱动系统均能改善带式输送机的启动性能,并实现调速功能,满足长距离,大运量的带式输送机运行要求。但液力耦合器结构复杂且易泄露,污染环境;液黏性调速器设备主要依赖于进口,成本较高;变频驱动会造成谐波污染;并且以上驱动系统仍然离不开“异步电机+减速器”的传统驱动形式,存在环节多,传动效率低,电机耗电量大,能耗损失大的问题。因此传统的驱动方式在大功率、高效率的发展趋势下面临着不小的挑战。
永磁电机因具有输出扭矩大,无励磁损耗,调速范围广等优点[5-7],在提升机、风机、刮板输送机等机械设备上永磁电机得到广泛应用[8-10]。鞠锦勇等[11]通过对永磁直驱式刮板输送机的扭振失稳现象进行理论分析,为永磁电机驱动下的刮板输送机系统的稳定运行提供理论依据;Sheng等[12]为了提高永磁电机驱动下采煤机的稳定性,构造了非线性反馈控制器;吴春华等[13]对用于风机水泵的永磁同步电机,设计了一种无传感器矢量控制系统;庄尚等[14]构建了一种基于数字信号处理器(DSP)的提升机永磁同步电机控制系统。也有学者在经验和技术应用方面对永磁电机在带式输送机性能上的表现进行了研究[15-16],为研究永磁直驱式带式输送机提供了重要的参考价值,但由于电机与输送机之间存在复杂的机电耦合关系,如何构建一个较为完整的永磁直驱式带式输送机系统模型还有待进一步深入研究。
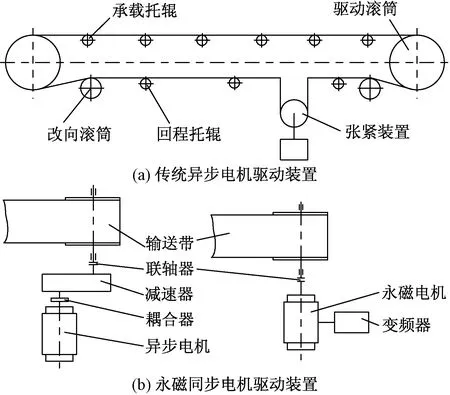
图1 带式输送机模型对比简图Fig.1 Comparison sketch of belt conveyor model
以永磁同步电机驱动的带式输送机为主要研究对象,分别研究带式输送机动力学模型和永磁同步电机状态方程,进而构建基于机电耦合关系的永磁直驱式带式输送机系统模型和能耗解析式,通过仿真重点分析了永磁电机驱动的带式输送机和异步电机驱动的带式输送机的张力和能耗差异,为永磁直驱式带式输送机能耗分析的研究提供了理论依据。
1 永磁直驱式带式输送机系统模型
永磁直驱式带式输送机模型简图如图1(b)所示,由于没有“减速器+耦合器”的组合结构,因此电机输出的驱动力矩可通过联轴器直接作用于驱动滚筒,进而带动输送带工作,输送物料。
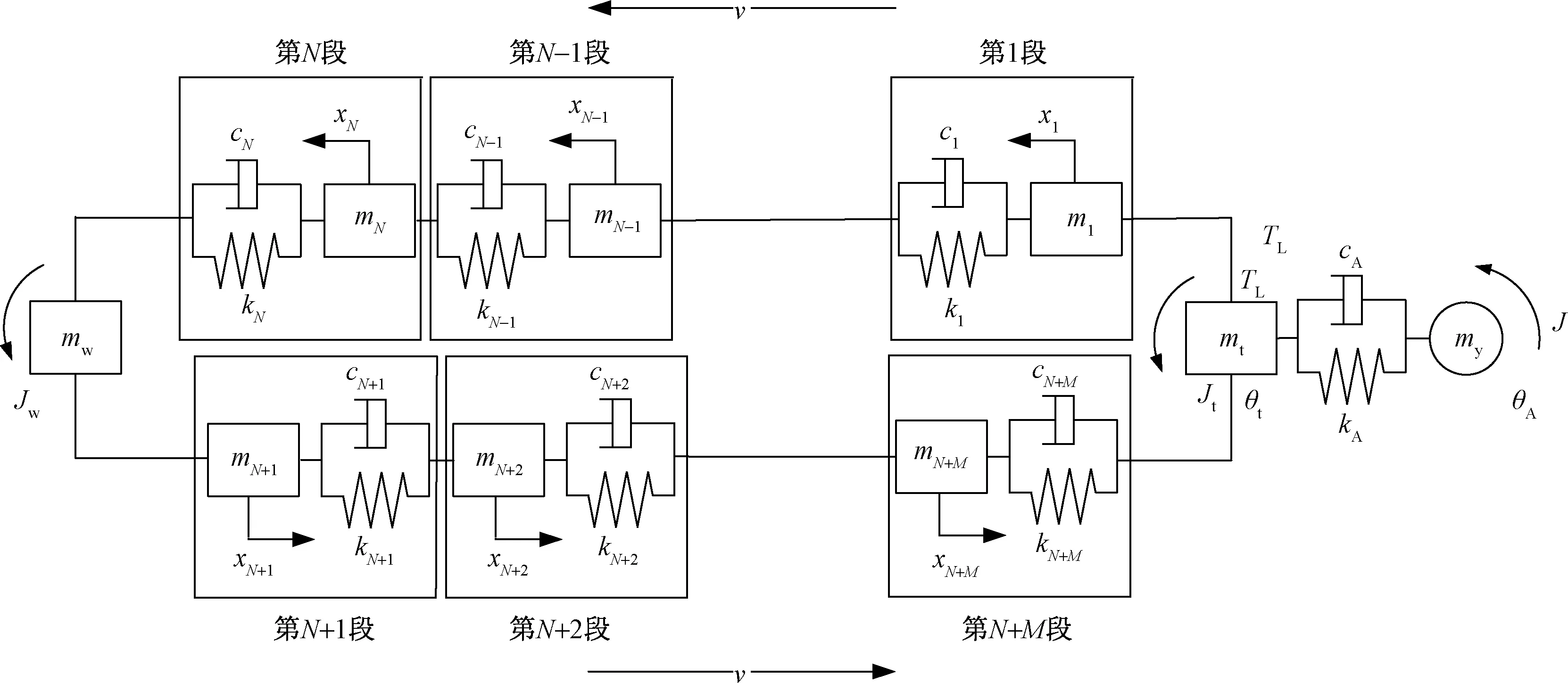
图2 永磁直驱式带式输送机动力学模型Fig.2 Dynamic model of permanent magnet direct drive belt conveyor
在实际运行过程中,带式输送机的动力学特性较复杂,为了简化模型,采用微元法将整个系统拆分成若干各单元,将连续型转化为离散型研究,并做出以下假设。
(1)各单元的托辊,物料以及输送带的等效质量均匀分布,运行阻力在各单元沿带长度均匀分布。
(2)物料和输送带保持一致的速度前行,且物料与输送带之间不存在惯性阻力。
(3)缠绕在滚筒处的输送带与滚筒之间不会产生相对滑动,且该处输送带质量可忽略不计。
(4)忽略输送带的横向振动影响。
1.1 带式输送机动力学模型
将带式输送机的上、下部分各分成N段和M段,构建N+M个有限单元体,各质量单元间通过Kelvin-Vogit模型进行连接,得到永磁直驱式带式输送机的动力学模型如图2所示。图2中,ci(i=1,2,…,M+N)为各单元的黏性阻尼系数;ki为各单元的刚度系数;xi为各单元的位移;mi为各单元产生的位移;cA为联轴器的黏性阻尼系数;kA为联轴器的刚度系数;TL为负载转矩;J、Jt、Jw分别为永磁电机、机头、机尾滚筒的转动惯量;my、mt和mw分别为永磁电机、机头滚筒和机尾滚筒的质量;θA、θt分别为永磁电机、机头滚筒的转角。
通过上述模型可得到动力学方程为

(1)
令X=[x1x2…xM+N]T,式(1)可表达为
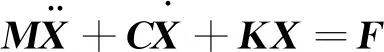
(2)
式(2)中:M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;F为外力矩阵,包括作用在驱动装置上的转矩,以及各单元受到的摩擦力。各矩阵表达式为

(3)

(4)
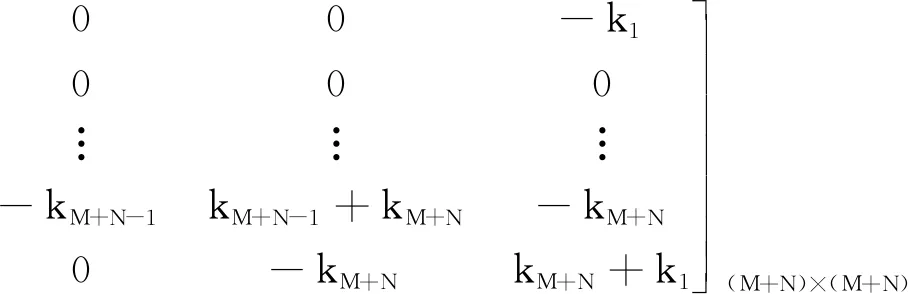
(5)
1.2 永磁同步电机模型
在满足忽略铁心饱和,不计涡流和磁滞损耗,没有受到阻尼作用,各相绕组对称的条件下,可得d-q同步旋转坐标系下的状态方程:

(6)
式(6)中:第1个方程为电机运动方程;iq、id分别为交轴电流、直轴电流;uq、ud分别为交轴电压、直轴电压;Lq、Ld分别为交轴电感、直轴电感;W为转子机械角速度,W=w/pn,其中w为转子电角速度,pn为电机极对数;Te为电磁转矩;J为转动惯量;B为黏滞摩擦系数;Rs为每相绕组线圈的电阻;ψf为永磁体磁链。
1.3 带式输送机-永磁电机机电耦合系统模型
综合建立的带式输送机模型和永磁同步电机模型,可以得出:永磁电机驱动系统通过式(6)中的电机运动方程输出电磁转矩和转速,并作用于带式输送机系统,带式输送机系统又根据式(1)将负载转矩反馈给永磁电机驱动系统,进而形成带式输送机-永磁电机机电耦合系统模型,具体机电耦合关系如图3所示。

图3 带式输送机-永磁电机机电耦合系统Fig.3 Electromechanical coupling system of belt conveyor and permanent magnet motor
1.4 能耗模型
当永磁同步电机在启动阶段时,为了提高启动性能,减少启动阶段时的动应力,系统采用带有延时段的Harrsion软启动速度模型[17],得到图4所示的S形曲线,其表达式为

(7)
式(7)中:vm为输送带稳定运行的速度;v0为输送带爬行段速度;t0为进入延时段的时间;t1为进入爬坡段的时间;t2为整个启动时间。
由电机学得到电机驱动转矩与功率关系:
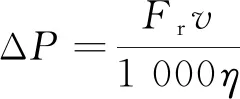
(8)
式(8)中:ΔP为Δt内消耗的功率,其中Δt表示单位时间变化量;Fr为运行阻力;η为电机效率。
假设满足η=TL/Te,则由式(6)的电机运动方程和式(7)、式(8)得到启动阶段单位时间内消耗的功率为

(9)
所以整个启动过程永磁直驱式的能耗(Q)为

(10)
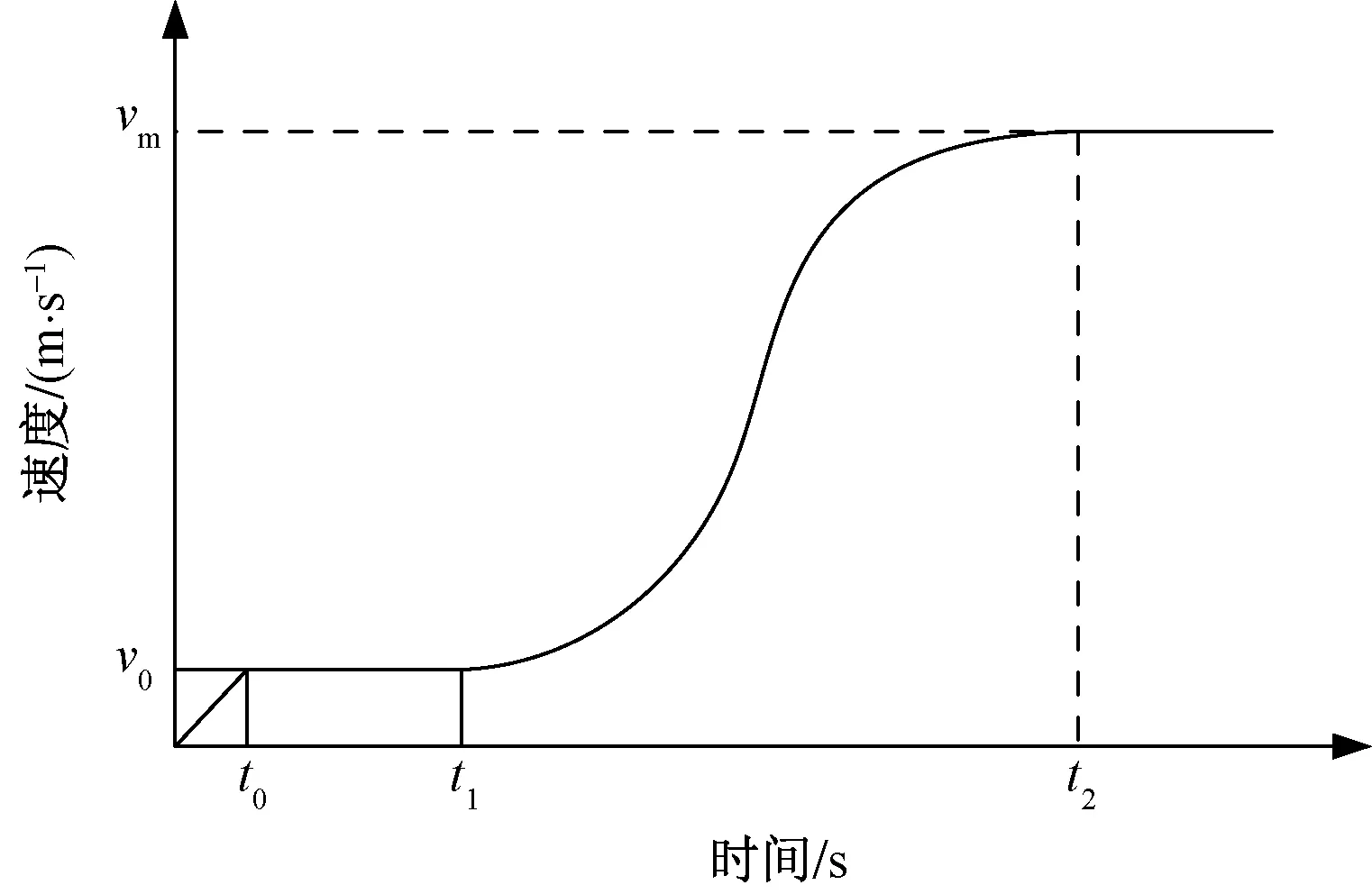
图4 带爬行段的S型曲线速度Fig.4 S curve velocitywith crawling section
2 系统仿真与分析
2.1 机电耦合系统仿真
由于永磁直驱式带式输送机具有复杂的非线性机电耦合关系,不易求出解析解,因此一般采用近似法和数值法进行求解。在MALTAB/Simulink软件环境中搭建了系统模型(图5),得到基于机电耦合关系的永磁直驱式带式输送机的动态特性。假设带式输送机在满载下进行启动,Harrsion软启动速度曲线中t0=10 s,t1=30 s,t2=100 s。仿真中的主要参数如表1所示。
在该系统模型中,以Harrsion软启动速度作为程序控制的初始条件,并在同步旋转下通过id=0(转子磁链定向)的矢量控制方式构成驱动系统;驱动系统输出的电磁转矩带动带式输送机系统运行,同时带式输送机系统产生的负载转矩反馈给驱动系统,形成了驱动系统与带式输送机系统的机电耦合关系;进而在机电耦合系统输出的转矩、转速等参数的基础上,由电机学基础理论构建能耗系统。
图6为S型启动机头、机尾的速度对比。由图6可知,启动初始,带式输送机由于要克服系统的摩擦阻力,带块的速度波动较为剧烈;经过20 s的爬行段后,速度曲线趋于平滑;由于张力从机头传递至机尾需要时间,所以机尾的平缓时间大约慢于机头10 s;100 s后,系统启动阶段结束,带速也达到预设工况的2.1 m/s;之后经过50 s的平稳运行测试,速度曲线未发生振荡,系统运行平稳。

PI表示比例和积分线性控制器;fi表示各段运行阻力;Q表示系统产生的能耗;xi表示输送带各段位移; x1表示从输出的各段位移种选择第一段位移输出图5 永磁直驱式带式输送机系统仿真模型Fig.5 Simulation model of permanent magnet direct drive belt conveyor

表1 仿真参数

图6 S型启动机头、机尾速度Fig.6 Head and tail speed during S type starting
选取机头、机尾和回程中间段3个单元对该系统进行进一步分析,结果如图7所示,3处张力变化趋势一致,整个带式输送机系统在机头处所受张力最大,而机尾处张力最小,符合实际运行工况;结合图6速度曲线可知,在30~100 s这一过程中,由于瞬时速率以从小到大再到小的规律变化,使得张力增大至此过程的峰值后再逐渐降至平稳运行时的张力。

图7 S型启动特殊单元张力对比Fig.7 Comparison of tension of special unit during S type starting
2.2 不同驱动方式对比
2.2.1 张力对比
为了验证永磁直驱式带式输送机在性能上的优越性,基于相同的带式输送机系统,选取额定功率和转动惯量与永磁同步电机一致的异步电机,搭建异步电机驱动的带式输送机系统。其中为确保与永磁同步电机的矢量控制方法相符,根据转子磁链定向控制方法[18],在旋转坐标下对异步电机进行矢量控制。异步电机参数如表2所示。

表2 异步电机参数
考虑到机头处张力最大,最容易进行分析,因此将机头处的张力作为系统仿真的对比点。图8为永磁直驱式与传统异步电机驱动式对比图,由于永磁电机调速范围广,能够以极低的转速启动,因此刚启动时张力峰值远小于传统异步电机驱动式;50 s以后,永磁电机转速仍在缓慢增加中,转速的增加导致张力依旧有轻微波动;100 s启动结束后,张力趋于平稳。由以上分析过程可知,永磁直驱式带式输送机具有更低的张力峰值,在实际应用中,低张力意味着能采用强度相对低的胶带,这不仅能提高带式输送机的经济效益,同时能够减少整机的宽度,节省了整机所占的空间。

图8 永磁电机和传统异步电机机头张力对比Fig.8 Comparison of head tension between permanent magnet motor and traditional asynchronous motor
2.2.2 能耗对比
为了更好地分析两种不同电机驱动产生的能耗,将异步电机通过变频器进行相同的调速处理,由图9驱动力矩对比可知,当系统趋于平稳之后,异步驱动式驱动转矩略高于永磁直驱式驱动转矩,由于机械效率在两种驱动方式中不一致,导致两种驱动方式在负载一致的情况下,异步驱动式的功率损耗偏大,所需的驱动力矩也更大。

图9 S型启动驱动力矩对比Fig.9 Comparison of drive torque during S type starting
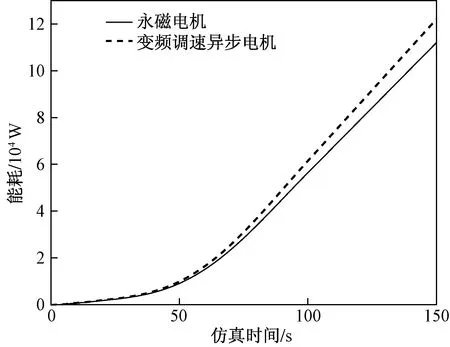
图10 S型启动能耗对比Fig.10 Comparison of energy consumption during S type starting
图10为两种驱动方式在S型启动时的能耗对比,在启动初始,结合图9可以看出,驱动力矩差距较小,因此两种驱动方式各自产生的能耗未产生较大差距;50 s后,两者之间的能耗差距逐渐增大,在经过整个150 s仿真过程后,永磁直驱式带式输送机能耗约为1.12×105W,而异步驱动式带式输送机为1.22×105W,永磁直驱式能耗约为异步电机的92%。由以上能耗分析,综合式(9)和对转矩的分析可以看出,在转速一致的情况下,能耗主要与转矩有关,而异步驱动式所需驱动力矩更大,因此永磁电机能够提高能源的利用率,满足现今大功率,高效率的发展趋势要求。
3 结论
(1)在以Kelvin-Vogit模型构成的带式输送机离散系统的动力学模型基础上,引入同步旋转坐标下的永磁同步电机状态方程,建立起基于机电耦合关系的永磁直驱式带式输送机系统,并推导了带式输送机在启动阶段的能耗解析式,为研究机电耦合关系下的永磁直驱式带式输送机提供理论参考。
(2)以Harrison软启动速度作为仿真模型的初始条件,得到系统的动态特性,仿真结果表明了所搭建模型的带速和张力变化规律符合实际运行工况;进一步将异步电机驱动的带式输送机系统于永磁同步电机的带式输送机相比较,结果表明永磁直驱式带式输送机在启动过程中,具有更小的张力峰值,并节约了8%左右的能耗。
