在初中数学教学中培养学生的创新思维能力探析

王秀敏

【摘要】创新是素质教育的着眼点，教育需要创新。数学教学大纲强调：“发展思维能力是培养能力的核心，而在各种形式的思维中，创新思维是培养的重点。”因此，培养学生的创新思维能力，任重而道远。本文从初中数学教学中，运用问题情景的设置、教学方法的优化及进行题组训练等方法，引发学生的创新意识，使学生感受知识产生和发展的过程，培养和发展学生的创新思维能力等方面进行论述。

【关键词】问题情景;教学方法;题组训练;创新思维能力

创新是一个民族进步的灵魂，是一个国家兴旺发达的不竭动力。创新就是用独特新颖的方式，使学生在学习中逐渐发展个性，富有创造力。新课标强调培养学生的数学素质，而素质教育的核心在于学生创新能力的培养。数学教学要让学生学到丰富的知识，更重要的是要掌握获取知识的方法，从而拓展学生的思维空间和创新能力。

数学问题既抽象又千变万化，思路、方法不可能千篇一律，单纯的模仿和记忆不利发展学生的个性思维，所以数学教学要创新，要想方设法让枯燥的知识变得有“活力”，使学生始终处于积极的学习状态，获得参与创新性的机会，创新思维能力得到培養。

—、设置有效的问题情景，引发创新意识

陶行知先生说：“发明千百万，起点是一问。”问题是数学的心脏，是创造思维的源泉。在教学中，应有意识地创设问题的情境，激发学生求知的欲望，引发创新意识。

（一）创设问题情境应有趣味性、有启发性

例如，在学习《正方形判定》时，笔者创设如下问题情境：小林想要检验一条毛巾是否是正方形，于是她拉起一组对角，看是否对齐，又拉起另一组对角，看是否对齐，小林的这种办法可行吗？如果是你会采用什么办法呢？这样的问题情境，使学生感到有趣，产生一种非寻求不可的意念，从而积极思考，直到解决问题。

（二）结合数学小实验，从“做数学”到“想道理”，获得直接经验

如，教学 “三角形的三边关系”时，笔者事先准备好一些长短不一的木棒（标有长度），提出问题（1）取出任意三根木棒都能组成三角形吗？学生七嘴八舌，有说能，也有说不能，让学生自己动手演示，得到结论：有的能，有的不能。接着笔者取出任意三根，先判断能还是不能，再演示，结果每次都准确无误，学生感到很神奇，这时又提出问题（2）三根木棒能否组成三角形，跟什么有关？学生肯定会回答（长度）。再提问（3）跟他们的长度有什么关系呢？学生学习热情会很高涨，知识点的学习水到渠成，学生还能进一步解决如 “已知两边求第三边的范围”及相关的问题。

可见，有效的问题情境，使“看”“做”“想”统一起来，知识变得“有趣”“易学”，自然而然引发学生的创新意识。

二、优化教学方法，培养创新思维能力

教学方法多种多样，选择的方法要使学生在发现和探索数学问题中，学会一定的思维方法，思维不断得到训练，形成良好的数学思维习惯，促进创新思维能力的发展。

（一）活用类比法，培养创新思维能力

类比，是一种思维跳跃，借助类比，可以发现新领域里的新结论。教学中有意识地对相关知识进行比较，找出其异同点，突出知识之间的纵横联系，以此获得更新、更高的理解。所以说类比是培养学生创新思维的一种重要方法。

例如，分式同分数作比较，它们有不少相同的属性：分子和分母乘以同数（或同式）结果不变;分母相同的分式相加减与分母相同的分数相加减，有相同的运算法则。根据这些属性的类似，可类推出在分母不同的情况下，分式和分数的加减运算法则也相同。

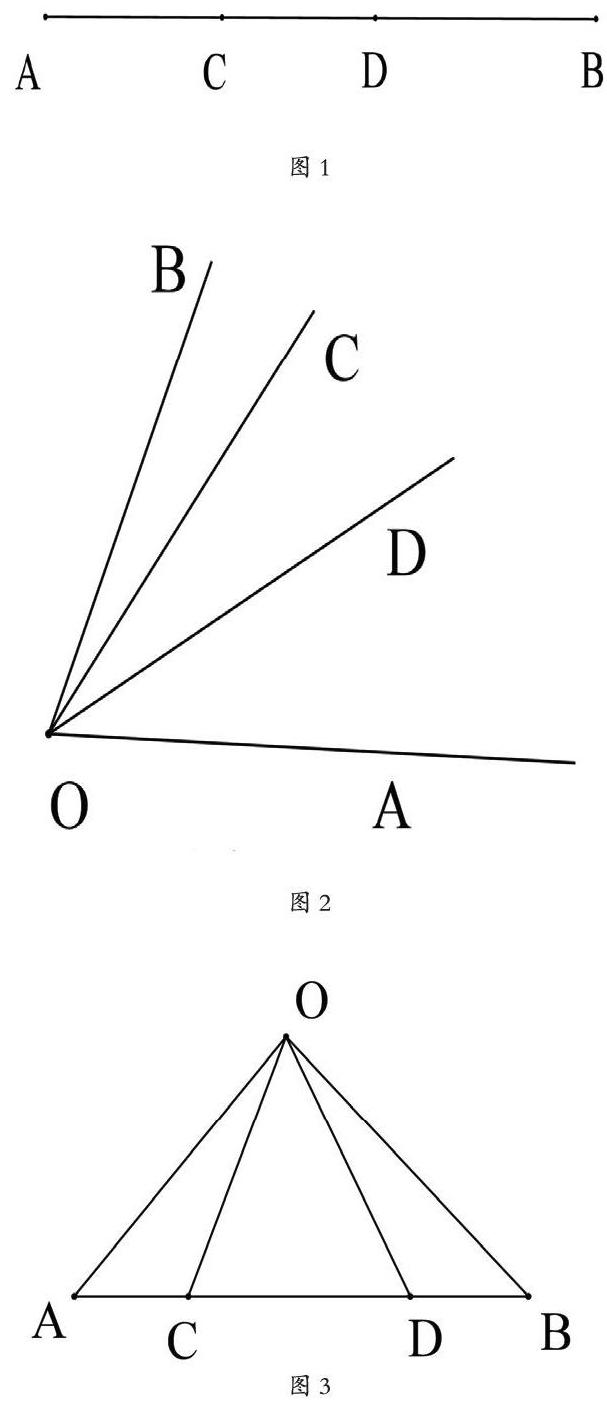
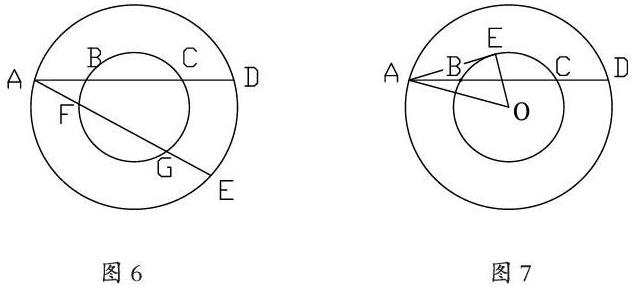
又如：图1数一数共有几条线段？图2数一数共有几个角？图3数一数共有几个三角形？

由线段、角、三角形的概念可知，图1从端点A数起，点A到点C、D、B有3条线段，再从点C到D、B有2条线段;图2从射线OA数起，射线OA与其它三条射线可以构成三个角，再从射线OB数和其它两条射线可构成两个角……这样有序的数，便不重不漏，同理图3可很快得出总数。然后，图1的端点增加，图2、3的射线增加，同样可以得准确的总数。这样，从数线段到数角再到数三角形，活用类比法，一法多用，学生记忆深刻，同时提高学生的创新思维能力。

（二）体现化归思想，促进创新思维能力的发展

在数学解题的过程中，逐渐把化归思想渗透到学生的认知结构中去，由具体向抽象化归（前进），或由繁到简化归，潜移默化，有意识地将问题转化为已经解决或较易解决的问题，同时，注意深入浅出，增进学生学好数学的信心，获得探索数学问题的思维方法，促进创新思维能力的发展。

如，在学习同类项法则时，笔者出一系列式子：“2+1=？”与“2-1=？”，“2△+△=？”与“2△-△=？”，“2x+x=？”与“2x-x=？”，“2（x+y）+（x+y）=？”与“2（x+y）-2（x+y）=？”，“2x2y+x2y=？”与“2x2y-x2y=？”等等，

再如，应用题的学习也可以从具体的问题情境中抽象出数学问题，归结为某一数学模型、获得合理的解答，从而促使学生形成良好的数学思维习惯，促进学生创新思维能力的发展。

（三）巧用计算机辅助，转化思维形式

丰富的信息技术资源，多种感官的综合刺激，有利于学生对数学知识的获取与保持。特别是几何中点的移动，线和图形的变化，都可以利用《几何画板》或智能教学平台，通过设置、鼠标拖动等操作来展示动态，揭示知识的形成过程，使学生由形象思维转为抽象思维。

如，“图形的平移”，先选中平移方向及平移距离，再选中平移对象即可完成平移，形象地显示了平移前后图形的形状、大小不变，加上平面直角坐标系还可以明确点的坐标变化与平移方向的关系。计算机的动态变化将形与数有机结合起来，思维更深刻。

三、进行题组训练，发展创新思维能力

学生思维的创造能力是在一般思维的基础上发展起来的，是思维能力培养的高层次要求。数学教学要防止机械的重复训练，要进行有效的题组训练。可以精选一些有代表性、巩固性和灵活性的习题，进行 “一题多解”“一题多变”等题组的训练，使学生能举一反三、触类旁通，创新思维得到发展。