“问题提出”教学，助推学生高阶思维能力发展

叶芳结

郑毓信教授在《数学教师的三项基本功》一书中提到：“学生提出问题的能力的培养应该被看成教学工作所应追求的一个更高的目标，即由被动地按照教师提问去进行思考，逐步过渡到由他们自己去提出问题。”提出问题是问题解决的开始，当学生能够提出真实而有价值的问题就是意味着学生开始从粗浅的好奇心逐渐转向有理智的好奇心。这种问题意识是问题解决、学会学习、创造性和批判性思维的萌芽。“问题提出”是教师运用学生提问来设计和推进教学，有别于传统的“教师提问——学生解答”的课堂教学形式，通过自主探究，让学生参与知识建构的过程，最大程度地将“被讲解”“被接受”的知识解放为“被认知”的状态，实现学生学习能力、实践能力与创新能力的培养与解放，助推高阶思维能力的发展，提升数学素养。

一、以“问题提出”为导向，助力概念理解

数学概念的建构，需要经历表象建立和丰富的过程。数学概念的理解与掌握，不仅仅只需要知道相关的文字描述，它更需要体现在多角度思维把握的过程中。可是我们在概念教学尤其是建立概念的教学中，常常会忽视概念的形成过程，注重通过背诵记忆和大量练习，让学生快速熟悉知识和技能。对概念所包含的丰富内涵理解不够，学生的体验少，记得快忘得也快。在概念教学中，我们的着眼点是学生知识的掌握、能力的形成和数学思考的思想与方法。概念教学最理想的状态是教师创设问题情境，引发学生提出困惑，进而于碰撞与交流中提炼本节课的“核心问题”。

教学片断一：《圆的认识》

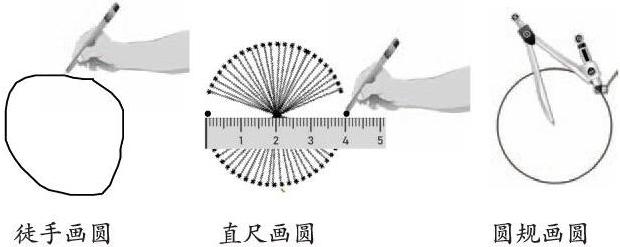
1.出示情境图，你能提出有关圆的数学问题让大家一起研究吗？

要求学生提出尽可能多的问题。

生1：为什么徒手画的圆不圆？

生2：为什么用圆规画的圆是圆的？

生3：用直尺也能画出圆的圆？

生4：圆有什么特点？

……

2.以小组为单位，挑选最值得研究的几个问题，在小组内合作交流，尝试解决。

3.小组代表汇报，说明挑选问题的原因及解决问题的方法。

圆是由曲线围成的平面图形，学生不能联系已有知识经验作正迁移，但圆对于学生来说并不陌生，大家都有徒手画圆的经验，在这一环节出示三幅情境图，引发学生思考，让学生提出自己真实的困惑和真正感兴趣的问题，在小组内确定最值得研究的问题展开交流、讨论，“为什么徒手画圆不圆？”“为什么圆规画圆是圆的？”“圆有什么特点？”实际上就是围绕“圆的本质属性”提出的，学生在小组合作解决问题的过程中不断辨析“圆是到定点距离等于定长的点的集合”，从而凸显圆的本质属性。“问题提出”教学，激发学生对知识点的深入探究，化被动为主动，在问题提出中有效聚焦核心问题，不断更新认知、理解概念本质，才能融会贯通，形成数学素养。

二、以“问题提出”为手段，促进合作建构

“数学问题提出教学”帮助学生深入理解数学知识和数学技能，将学生引向深度学习。数学问题提出的过程，既是对问题提出情境中蕴含的信息进行辨认和深入理解的一个过程，也是发现情境中蕴含的数学关系或矛盾，并借助语言或符号将其进行适当表达的过程。而小組合作学习不仅为每一个小组成员提供了表达自己想法的机会，也提供了了解伙伴想法的机会。不同的学生，学习经验、认知水平、生活经历会不同，他们学习数学的方式和结果也会千差万别，这些差异为学习提供了丰富的资源。

教学片断二：《长方形正方形面积与周长》练习课

任务一：设计两个求面积的数学应用题，使其答案为16。

任务二：编写两个计算周长的数学问题，使其答案为16。

要求：①先独立思考，然后在小组内交流自己的想法，组长做记录并检查编题是否正确;②每组至少编出2道不同的数学问题，并找出规律;③全班汇报。

对于面积是16，学生可以理解有16个面积单位，放1排，每排16个;放2排，每排8个;放4排，每排4个。对于周长是16，不少学生能联系正方形的周长是16，边长就是4，而周长是16的长方形，让学生逆向推导出长方形的长和宽。而对于部分学生来说，确实存在困难。周长与面积大多共同承载于一个图形之中，造成学生对面积表征与周长表征的混淆，学生在任务学习中提出问题，通过对问题的辨析，厘清图形的面积与周长的区别，学生在小组合作中发表自己的想法;在互相讨论中修正自己的错误;在交流中学会取长补短，学会倾听与表达、学会合作，促进了每一个人的思考和学习，以有价值的问题引领有意思的数学活动，给学生提供更多的自主探究、合作交流的时间和空间，真正地“使每一位学生在学习中都能得到发展，不同的学生在学习中得到不同的发展。”

三、以“问题提出”为策略，内化数学模型

爱因斯坦说过：“问题的提出比解决问题本身更有价值。因为解决问题的过程就是在提高自身的实践技能，而举一反三的提出有价值的问题，是需要具备聪明的大脑。”通过教师指导、学生互助，“问题提出”能够激发学生去观察、去思考、去实践，从而内化数学模型，提升思维能力。

教学片断三：《100以内数的加法与减法（一）》练习课

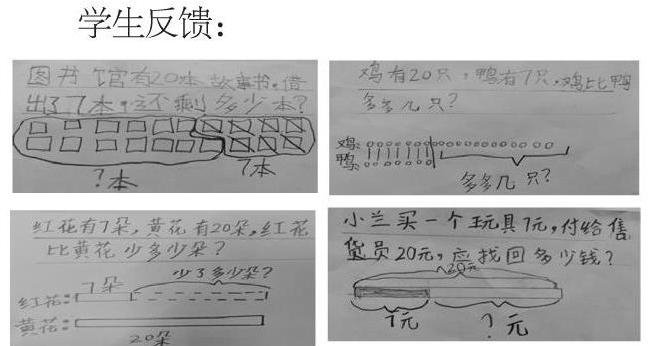
任务一：根据11+4=？这道算式，独立编写一个用加法计算的数学问题，再在小组内用画图的方法尝试解释这道题为什么用加法解决。

学生反馈：

任务二：根据20-7=？这道算式，独立编写一个用减法计算的数学问题，再在小组内用画图的方法尝试解释这道题为什么用减法解决。

学生反馈：

富有挑战性的问题提出，以及师生、生生互动交流，同时借助图示表达，学生自主地建立数量关系的数学模型，有了模型的支撑，凸显模型思想在解决问题中的重要性，学生从本质上理解加法与减法的含义——加法实质上就是部分数加部分数等于总数;而减法就是总数减去部分数，实现数学知识向数学思想方法的转化、升华和概括。

“问题提出”教学，使学生在学习中聚焦于问题的本身，改变传统教学观念，从有效的教走向有效的学，从知识掌握走向智慧生成，从碎片化知识走向系统的思维与整体的认知。提高学生的问题提出能力、问题解决能力与沟通交流能力的同时，发展学生数学高级阶思维，满足不同学生的需求，以实现学习机会的最大化、公平化。

参考文献：

[1]黄爱华，张文质.“大问题”教学的形与神[M].南京：江苏教育出版社，2013：107.

[2]丁玉华.小学数学典型概念课教学研究[M].长春：东北师范大学出版社，2018：23.

[3]史中宁.基本概念与运算法则：小学数学教学中的核心问题[M].北京：高等教育出版社，2013：46.