玻璃态聚合物焓松弛动力学研究进展

2020-12-28武建鹏刘国栋

广州化学 2020年6期

武建鹏，刘国栋

（河北工业大学化工学院，河北省功能高分子重点实验室，天津 300130）

在外界条件变化时聚合物的结构会向新的平衡态转变，聚合物的结构和性能也随之发生变化，这种变化通过分子运动实现。但是聚合物的分子运动速度慢，具有松弛特性，尤其在玻璃化转变附近更加明显，它影响着聚合物的各种性能，如密度、模量、强度、介电性能等。很多聚合物材料是在玻璃态结构下被保存和使用的，因此松弛现象及动力学研究对聚合物材料的长期使用性能有十分重要的指导意义[1]。另外，松弛动力学研究也与对玻璃化转变本质的认识密切相关[2]。

人们对聚合物材料松弛的研究最早为体积松弛[1,3]，随后焓松弛[4]、介电松弛[5]、力学松弛[6]、中子散射[7]等也被广泛研究，其中焓松弛通常采用非等温方式进行，可以很方便的同时考察温度和结构变化对分子运动松弛特性的影响，从而得到更多的松弛动力学信息，因此焓松弛成为研究聚合物松弛动力学的主要方式。模型的建立与验证是松弛动力学的核心所在，研究者建立了大量模型并对聚合物的焓松弛数据进行描述，取得了很大进展，研究表明聚合物的焓松弛具有非指数和非线性特征[4]，但是采用同一套模型参数描述焓松弛数据时往往与实验结果有系统偏差，为了更好地描述焓松弛数据，模型参数往往表现出不合理的热历史依赖性[8-11]，这与其作为材料特征参数引入相矛盾，说明目前的动力学模型还不能很好地描述聚合物的松弛过程。

对于变温过程，通常用假想温度Tf的变化来描述松弛的进行，由Boltzmann叠加原理可以求出材料在不同时刻的Tf：

式中，Tf(t)为任一时刻t时材料的Tf，Ti为平衡态下的起始温度，ϕ(x)为松弛函数，τ(T,Tf)为松弛时间，dTd为温度变化时材料对应平衡态的假想温度差。对式（1）进行求解需要对三个方面进行描述：1）聚合物平衡态性质，决定dTd数值；2）松弛时间-温度-结构关系，即τ(T,Tf)；3）松弛过程，即ϕ(x)[12]，本文对这三方面的经典理论和研究进展进行综述。

焓松弛是研究聚合物松弛及物理老化的重要方式，国内外有大量研究报道，并有对松弛及物理老化较为全面的综述文章报道，比如Hodge针对非晶材料焓松弛的非线性和非指数特性现象及描述、焓松弛参数进行了评述讨论[13]，Zhou对非晶食品糖类玻璃化转变与焓松弛进行了综述[14]，但一般都重点从非线性和非指数两个方面进行综述，另外最近有关玻璃态聚合物焓松弛领域又有一些重要进展。本文将从聚合物平衡态模型、松弛时间模型和松弛过程描述三个方面出发，并结合最新相关研究进展，紧密围绕焓松弛动力学模型进行综述。

1 聚合物平衡态性质

聚合物玻璃态是一种非平衡态，因此，焓值会随着时间自发地向平衡态数值转变。材料不同温度下的平衡态热力学性质是松弛动力学的基础问题，是松弛动力学乃至玻璃化转变最基础的研究内容。比较经典的有自由体积理论[15]、热力学理论[16]和动力学理论[17]。其中自由体积理论和热力学理论认为存在特征温度Tg（T0）或T2，温度低于此特征温度材料的平衡态热力学性质会偏离高温下平衡态的外推值，而动力学理论则认为并不存在任何特征温度，低温下平衡态的热力学性质与高温平衡态外推值完全一致，即在任何温度下dTd=dT，玻璃化转变现象完全由动力学因素导致。

对聚合物Tg以下的恒温焓松弛研究表明，材料的焓值会向高温平衡态外推值松弛，但是其松弛外推平衡值高于高温平衡态外推值[18-19]，如图1所示。Gómez Ribelles等假定在Tg以下聚合物焓值存在中间状态，提出GR模型，相对于假定玻璃态平衡态性质与橡胶态外推值一致的经典模型，计算结果与实验结果方差有一定改善[20]，Andreozzi等的研究表明模型结果和聚合物的缠结结构有关[21]。Cangialosi试图从实验证明该中间态的存在[22]，但是随后的长时间恒温松弛结果表明聚合物在Tg以下十几度的范围内并不存在中间平衡态[23]，但是对于更低温度下是否存在中间平衡态未见报道。这些表明聚合物在Tg以下是否存在中间平衡态仍然具有争议，因此对聚合物Tg以下的恒温焓松弛还需要更深入研究。

图1 焓松弛中间平衡态示意图[18-19]

2 松弛时间模型

由于松弛时间与黏度密切相关，对于松弛时间τ（或黏度η）与温度和结构的关系研究起步较早，基于玻璃化转变的不同理论，研究者建立了不同的松弛时间（黏度）模型，比较经典的有以自由体积理论为基础的 Vogel-Fulcher-Tammann（VFT）模型[24-26]、以构象熵理论为基础的 Adam-Gibbs（AG）模型[27]和从Arrihenius方程变形得到的Tools-Narayanaswamy- Moynihan（TNM）模型等[28-30]，如表1所示。

表1 经典松弛时间模型

(续表1)

在VFT模型中，当选取Tg作为参照温度，VFT方程则变形为著名的Williams-Landel-Ferry（WLF）方程[31]。VFT方程为线性方程，没有考虑结构对松弛时间的影响，材料在Tg附近及以下的松弛具有非线性特征，因此VFT方程与实验结果偏差很大[32]，于是学者们从不同角度对VFT模型进行了非线性修正，不同的修正模型及特点如表2所示。

表2 VFT修正模型

在表2的VFT修正模型中，VFTA模型相对于传统AGV模型能够更好地描述聚合物的焓松弛数据。但是Simon等的研究表明，在低温下即便材料达到平衡态，VFT方程可能也不能很好地描述其松弛时间[32]，这说明对VFT模型的研究仍待进一步深入。

在AG模型中，当假定ΔCp与温度成反比可得到：

此方程称为 Adam-Gibbs-Vogel（AGV）方程，优点在于在高温平衡态（Tf＝T）时与 VFT方程一致。此方程在松弛动力学中得到广泛应用，与实验数据拟合效果得到明显改善，但是所得D的最优值远远偏离VFT方程中D的典型值[8,35]，表明用同一D值不能同时描述玻璃化转变附近和Tg以上的松弛时间。

除此以外，还有研究者从其他角度提出了不同的松弛时间（黏度）-温度-结构模型，比如 Macedo、MYEGA模型等[37-38]，但松弛时间-温度-结构模型仍未取得定论。

3 松弛过程描述

大量研究表明，玻璃化转变对应的松弛过程具有非指数和非线性的特点，其非指数特性一般采用Kohlrausch-Williams-Watts（KWW）方程描述：

式中τ为特征松弛时间，Kohlrausch指数β为不大于1的正数。一般认为β由松弛时间分布或运动单元之间的协同效应决定[39]，温度、老化时间等对β都有影响，比如Sastry报道β随着老化温度的降低而减小[40]。但是目前变温焓松弛动力学研究中均将参数β作为固定值进行计算，这源于在采用时域KWW方程通过Boltzmann叠加原理计算松弛过程时不能够考虑β随温度的变化，见式（1），如果在焓松弛动力学研究中考虑β的温度和结构依赖性，可能会更好地描述实验结果，这是该领域的一个关键问题。

另外，Cangialosi等的最近研究结果表明，聚合物在Tg以下的恒温焓松弛过程包含两个不同时间尺度的松弛过程[23]，如图2所示，快松弛有相对较低的活化能，而慢松弛符合α松弛规律，但未作出明确归属。随后Ngai等尝试对双焓松弛过程进行归属，把第一段归于α松弛，第二段归于sub-Rouse模式[41]。这说明聚合物在玻璃化转变附近的松弛归属于不同尺度的运动单元，但目前双时间尺度的两段松弛机理尚未能从分子水平上做出合理的解释。以此为基础建立双时间尺度松弛模型，对焓松弛数据的拟合效果略有改善[12]。

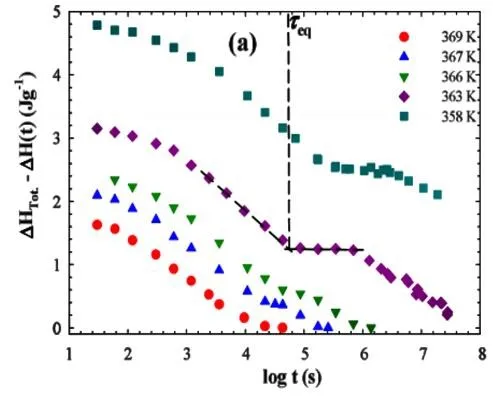
图2 两个不同时间尺度的焓松弛示意图[23]

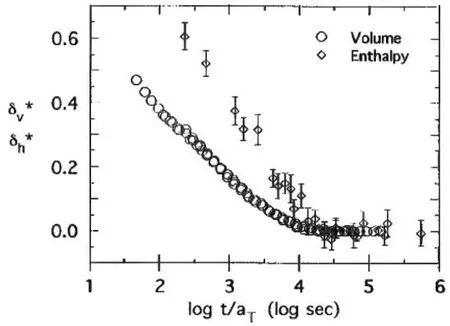
图3 PEI的焓松弛和体积松弛过程（归一化数据）[43]

除此之外，目前的松弛动力学模型通常采用单一假想温度Tf描述松弛过程，认为不同物理性能具有相同的松弛过程，但是Ritland早期研究指出单一假想温度并不能描述所有不同物理性能[42]，Simon等对PEI的研究表明体积松弛和焓松弛过程并不一致，体积松弛先于焓松弛发生，但是达到平衡所需时间基本一致[43]，如图3所示，这说明不同物理性能及结构的松弛过程可能不能用单一的松弛模型参数进行描述。如果在焓松弛动力学模型中对不同物理性能的松弛过程分别描述，有望能够更好地描述焓松弛实验结果。