含充填节理岩体中应力波传播规律的三维模拟
2020-12-28丁英勋王志亮黄佑鹏
丁英勋,王志亮,黄佑鹏
(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)
天然岩体被各种各样的不连续面切割,含有许多不同发育程度的节理、层理等结构面[1]。应力波的传播受到节理软弱力学性质及其复杂空间产状等影响。早期研究者就针对节理对应力波传播的影响开展了实验研究,并得到了诸如应力波通过节理面出现波速下降、波幅衰减以及波形转换等规律[2-6]。由于实验成本较高,目前数值模拟逐渐流行,并成为科研人员开展研究工作、补充试验的重要手段。近年来,国外学者广泛应用了二维离散元程序UDEC(Universal Distinct Element Code)来模拟应力波的传播,如Lemos[7]模拟了地震横波的衰减规律,表明UDEC适用于含节理模型的动力模拟;Brady等[8]模拟爆炸荷载作用下滑动节理对应力波传播的影响,得到了节理面抗拉强度较低时拉伸波较难通过节理继续传播的结论;Barton[9]通过模拟获得了P波通过节理组的数值解,发现节理数目越多透射系数越小。这些结果为国内研究更为复杂的工况,如不同的加载方式、边界条件及节理力学与几何参数等奠定了基础。Fan等[10]研究边界条件对P波传播的影响,得到了无反射边界可以将P波完全吸收的结论。赵坚等[11-12]分别模拟在P波以及爆炸荷载作用下含两组交错节理岩体的非线性变形等动态响应。杨风威等[13]模拟应力波斜入射节理时,透射、反射系数随入射角度、节理数目等的变化规律,并从角度和间距两个方面讨论了对称交叉节理对应力波传播规律的影响。刘婷婷等[14]研究了节理的初始刚度、间距、数量以及应力波幅值、频率和入射角度等因素对P波能量传递的影响。Zhu等[15]研究了应力波在多重交叉节理组中的传播,指出节理力学、几何参数共同影响应力波在节理岩体中的传播,发现入射角度和节理间的交叉角度均会影响应力波的衰减规律。虽然上述研究者针对不同形态的应力波通过节理或节理组的传播做出了由浅入深的研究,但二维UDEC的应用局限于模拟二维平面问题。实际情况中的节理具有不同的空间方位,且节理组的分布也不是等间距的排列。此时,三维离散元软件3DEC(Three Dimension Distinct Element Code)则有很好的适用性。但由于3DEC的应用较复杂,目前三维模拟研究只涉及地形地貌、单元尺寸、节理形状、节理刚度、波的形状与频率以及入射角等因素对波传播的影响[16]。
为拓展研究三维岩体中不同节理条件对应力波传播的影响,选用3DEC中的瑞利阻尼与黏性边界条件建立三维模型,并利用等效波阻抗理论来验证模型的正确性。在此基础上,继续研究充填节理的倾向方位角、视倾角、间距、厚度、数目以及入射波的频率对应力波通过充填节理的影响,并基于节理组与实际情况具有相似分布规律的假设,得到节理组的分布对应力透射、反射系数的影响。
1 模型建立及其验证
1.1 理论公式
为研究应力波通过层状充填节理发生透、反射的规律,李夕兵[17]基于应力和速度连续条件,提出了一种简便的方法,即等效波阻抗法。
假设一含充填节理岩体的节理厚度为h,波阻抗为z1,岩石波阻抗为z0,弹性应力波垂直夹层入射,如图1所示,其等效波阻抗Y为:

图1 应力波透射的等效波阻抗示意图Fig. 1 Schematic diagram of equivalent wave impedance for stress wave transmission
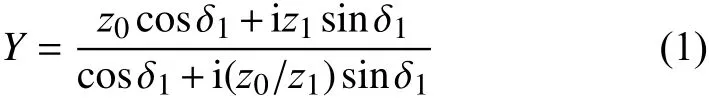
式中:i为虚数单位;δ1=2πh/λ1,λ1为波长。
则应力透射系数为:
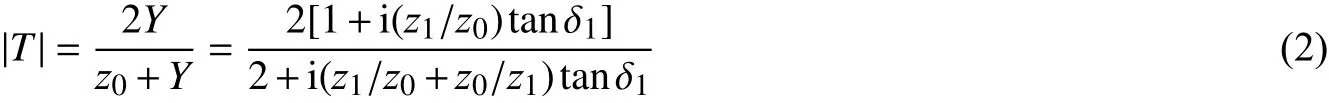
应力反射系数为:
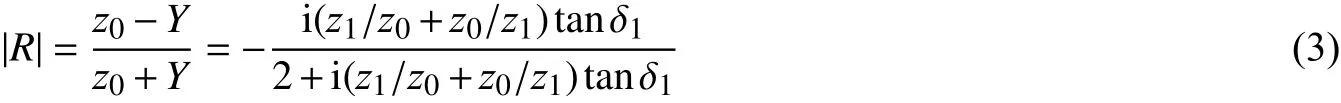
1.2 模型及参数
为验证3DEC模拟纵波(P波)在充填节理岩体中传播规律的可行性,建立1 m×1 m×150 m岩杆模型,如图2所示。模型的上下及前后边界均施加y与z方向的位移约束,且为了消除反射应力波产生的影响,左右边界采用无反射边界(能量吸收边界)。在x=90 m处设置充填节理,并分别在x=60 m和x=120 m处分别设置观测点A和观测点B。充填节理用两条人工节理(相当于充填节理的两壁)充当,两条节理的距离即为充填节理的厚度,并对充填节理材料赋予较低的物理力学参数。添加荷载为1个周期的正弦波,由左侧边界垂直入射,频率为100 Hz,波幅为1 m/s。
为了满足计算精度要求,网格尺寸与波长的比值要介于1/8~1/12[18]。岩石和充填材料的波长通过计算分别为57.0和2.7 m,因此岩石的网格尺寸划分为0.4 m,充填节理的网格尺寸划分为0.01 m。为了更好地与理论结果比较,节理的厚度采用2~12 mm。节理壁采用库伦滑移模型,岩石和充填材料均采用线弹性模型。充填节理采用位移应力连续模型,所以设置较大的黏聚力和节理壁刚度值以模拟充填材料产生位移。岩石和充填材料的力学参数如表1所示[16]。

图2 应力波通过充填节理计算模型Fig. 2 Calculation model of stress wave through the filling joint

表1 岩石与充填材料物理力学参数Tab. 1 Physical and mechanical parameters of rock and filling materials
岩石的体积模量K、剪切模量G与弹性模量E、泊松比υ换算公式为:

P波的传播速度cp计算式为:

1.3 动力输入及阻尼选择
在3DEC中,动力输入可以采用两种方式[18]:输入预处理过的速度时程;输入预处理过的应力时程。对于前者,如果是加速度时间序列,则需要通过数值积分转化成速度序列;如果是位移序列,则需要通过数值微分转化为速度序列。用户可通过FISH函数自定义荷载,即用BOUNDARY xstress或BOUNDARY xvel命令输入动力波荷载。但采用速度输入时,会在模型边界处发生反射。为了避免此情况,可以将速度记录转化为应力时程,按式(6)进行应力施加,并在边界上施加无反射(黏性)边界条件:

式中: σn为施加的法向应力;ρ为密度;cp为纵波波速;vn为施加的法向速度。由于需要克服黏滞边界效应,故式(6)中施加的应力均为应力波阵面上应力的2倍。
在3DEC中,由于输入能量后系统会在平衡位置产生震荡效应,因此需施加阻尼来耗散系统在振动过程中的动能。在岩土介质中通常选用的阻尼要比弹性系统大。软件中常用的阻尼有3种:Rayleigh阻尼、自适应阻尼及库伦阻尼。相比较而言,Rayleigh阻尼综合考虑了质量阻尼和刚度阻尼对系统的影响,并且能选取频率谱上对应的优势频率。于是选用Rayleigh阻尼,假设动力方程中的阻尼矩阵C与刚度矩阵M和质量矩阵K有关:

式中:i、j分别为质量阻尼比例系数与刚度阻尼比例系数,由式(8)确定:

式中:ξmin为临界阻尼比;ωmin为圆频率,其意义见图3。对于岩石或土,ξmin取2%~5%即可。
基频的定义为fmin=ωmin/(2π),可由以下公式计算:

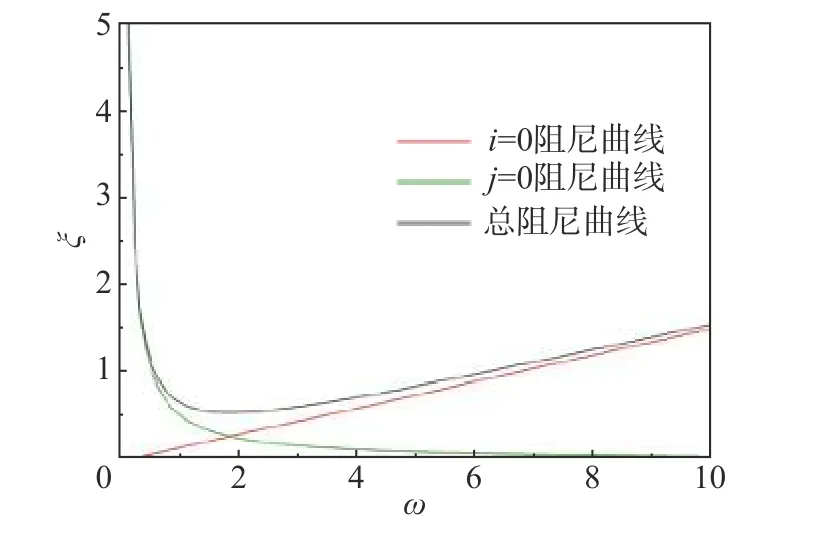
图3 阻尼曲线Fig. 3 Damping curve
式中:k为节理刚度(Pa/m);a为节理面积(m2);m为岩石块体的质量(kg)。
1.4 模拟与理论结果对比
透射系数定义为透射波幅与入射波幅的比值,反射系数定义为反射波幅与入射波幅的比值。在入射波频率为100 Hz,节理厚度在2~12 mm变化时,测点A、B处得到的波速曲线如图4所示。图4中可以看出透射波的波形与入射波一致,反射波为先上凸后下凹再上凸,表明入射波通过节理面处发生连续反射,且随着节理厚度的增加,透射波的波幅略微减小,反射波幅增大。关于透射、反射系数与充填节理厚度h的关系,数值模拟结果与理论计算结果对比如图5所示。可以看出,当充填节理厚度增加时,由于充填材料的弹性模量较低,使得吸收和耗散的能量更多,所以透射系数更小,反射系数更大。3DEC模拟和等效波阻抗理论法计算得到的结果较吻合,说明采用上述数值模型研究应力波在充填节理岩体中的传播规律是可行的。图6为入射波频率为100 Hz,节理厚度为4 mm时,不同计算时刻的x方向速度云图,显示了在0~17 ms时,正弦应力波从左端边界传播到节理面处,在17~27 ms时入射波分别完成透射(右行)和反射(左行),在27~38 ms时透射波与反射波分别被左右端面的黏性边界吸收。
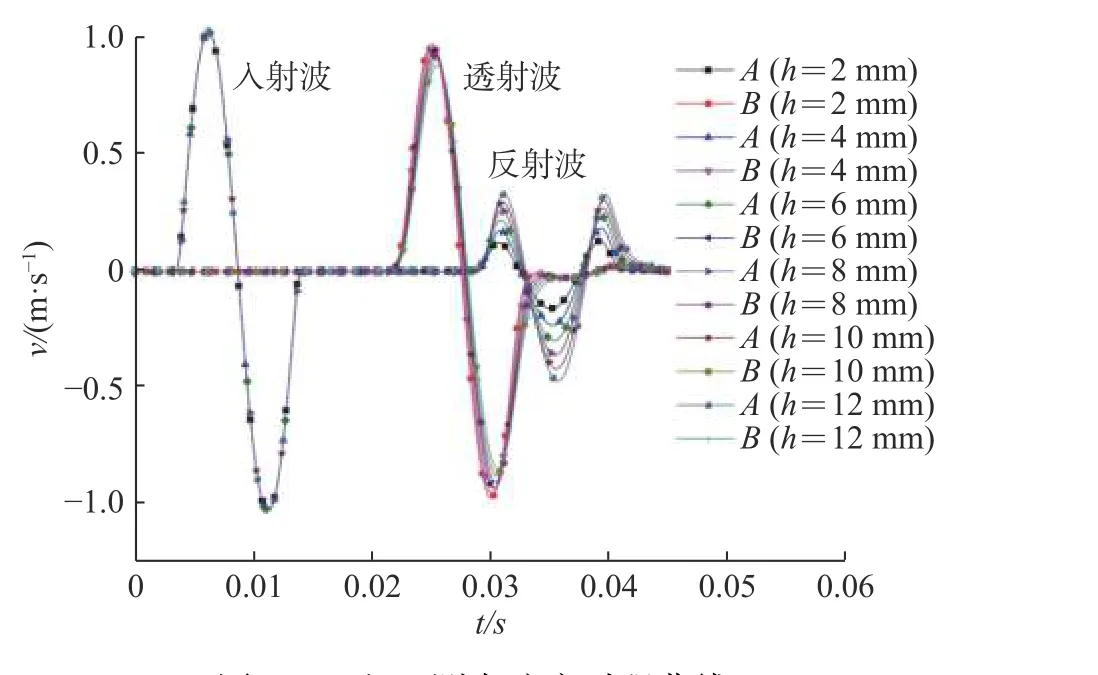
图4 A和B测点速度时程曲线Fig. 4 Velocity time curves of points A and B
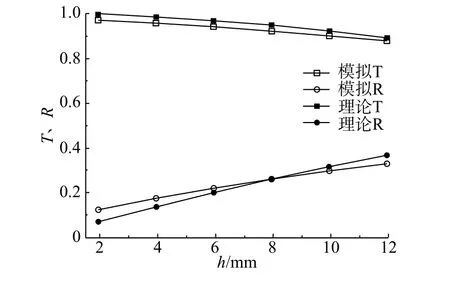
图5 充填节理厚度对透射、反射系数影响Fig. 5 Influence of joint filling thickness on transmission and reflection coefficients
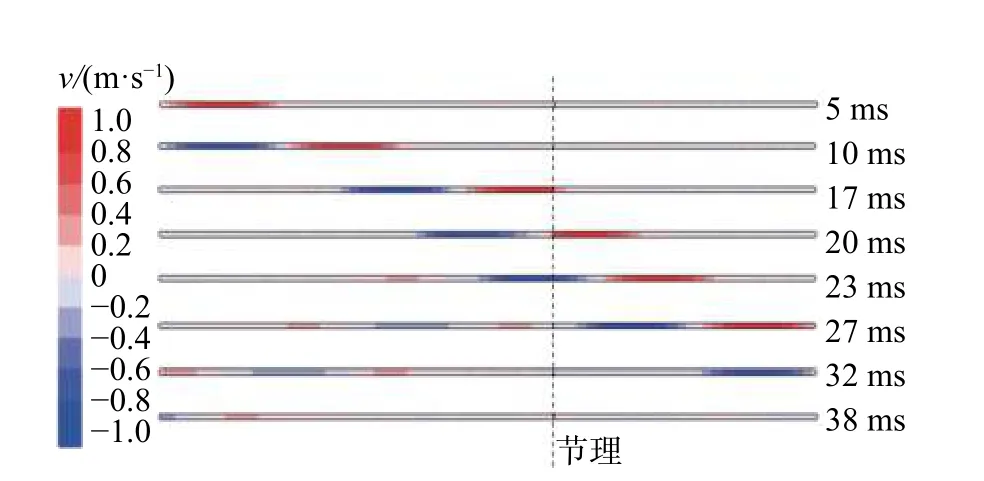
图6 岩杆不同时刻速度云图Fig. 6 Velocity contour of rock bar at different time
2 各参数对透射、反射系数的影响
2.1 节理倾斜角度
由于节理在空间产状分布的复杂性,在研究单一节理的产状对应力P波传播的影响规律时,定义两个角度变量:节理的视倾角为节理层面与前端面的交线与其水平投影的夹角(如图7中α),倾向的方位角为节理倾向与北方向(y轴)顺时针旋转得到的夹角(如图7中β)。预先分别设置充填节理厚度为2、4、6、8、10、12 mm,入射波频率为 100 Hz。这里先讨论单一节理视倾角α在15°~90°变化对透射系数和反射系数的影响。
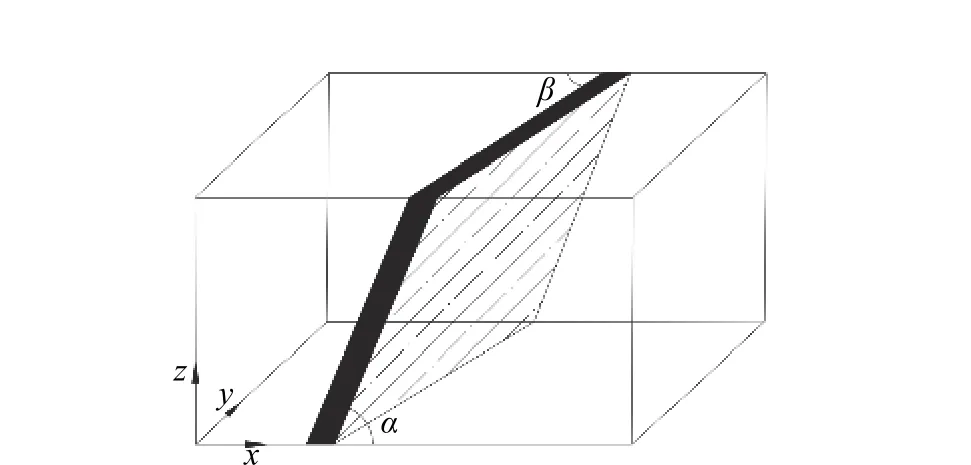
图7 节理的视倾角、倾向方位角示意图Fig. 7 Diagram of dip angle and azimuth angle of joints
图8 和9分别呈现了透射、反射系数在不同节理厚度下随α的变化。从图8可以看出,α在15°~60°变化时,透射系数随α的增大而减小,反射系数反之,且α在小于45°时透射系数降低的速率较大;当α在60°~90°变化时,透射系数随α的增大而增大,反射系数反之。此外,当角度较小时(15°),透射、反射系数对厚度的变化不敏感;当角度增大至45°以后,不同节理厚度在同一角度下的透射系数的差值也近似相等。这是因为当α很小时,节理的倾斜角度对应力波的传播阻碍较小,节理的面积成为主要的阻碍因素;当α逐渐增大时,倾斜角度对波传播的阻碍效果越来越明显,并且截面积变小导致其对波传播影响越来越小;当α增加到60°左右时,应力波传播的视倾角和截面积对应力波传播的综合阻碍效果达到最大,故透射系数达到最小值;随后α继续增加时,由于截面积逐渐减小,角度的增加成为影响透射系数的主要因素,故透射系数升高。反射系数有着与透射系数近似相反的变化规律,如图9所示,在此不做赘述。
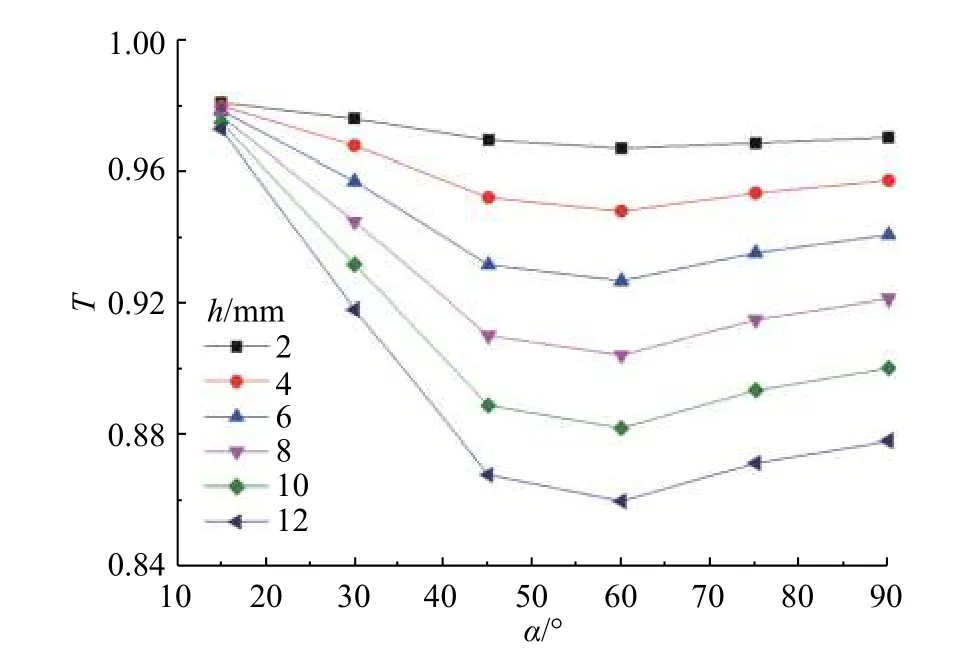
图8 不同α角度下的纵波透射系数Fig. 8 Transmission coefficients at different dip angles

图9 不同α角度下的纵波反射系数Fig. 9 Reflection coefficients at different dip angles
当考虑三维问题时,视倾角和倾向方位角同时在15°~90°变化,得到了透射系数与反射系数随α、β同时变化的三维图,如图10和11所示。可以看出,透射系数在0.877 5~0.981 5间变化,且在α=β=15°附近时透射系数达最大值,当图线仅沿α轴或β轴方向变化时,此时透射系数的变化幅度最小。这说明当α为15°时,β的变化对透射系数的影响很小,较小的角度对透射系数起决定性作用。观察图线在α=β截面上变化,可看出此时曲线变化的幅度最大,α、β从15°到60°变化时,透射系数逐渐降低,并在60°时为极小值,随后角度增加到90°时,透射系数逐渐增加。
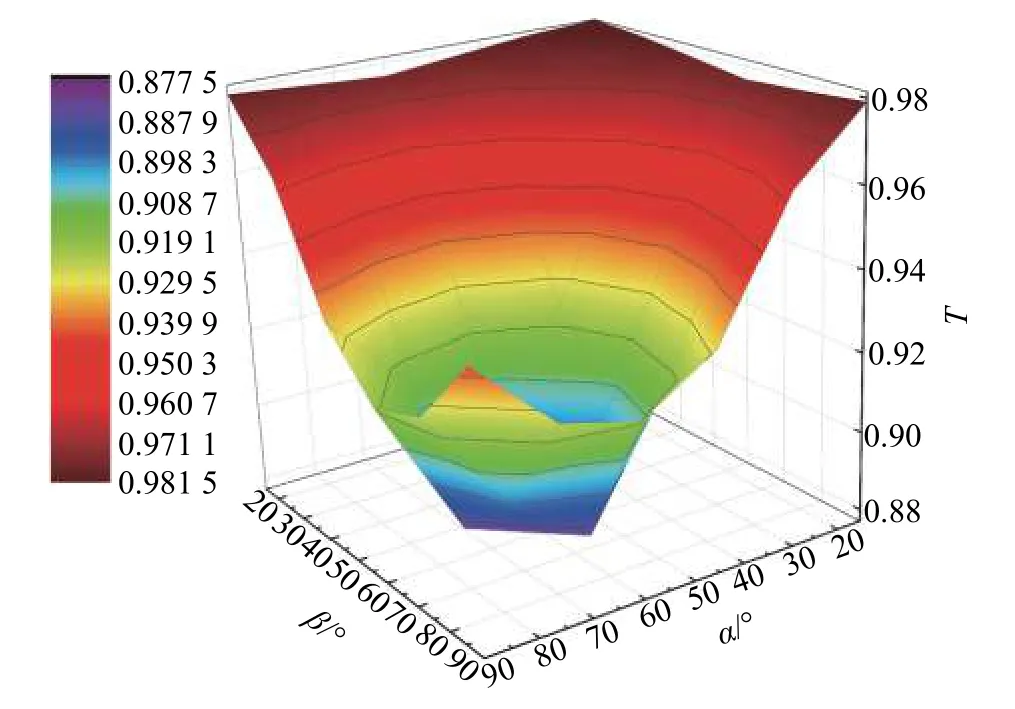
图10 不同α、β下的透射系数Fig. 10 Transmission coefficients with different α and β

图11 不同α、β下的反射系数Fig. 11 Reflection coefficients with different α and β
从整体观察可知,α(或β)从15°变化到60°时,透射系数沿着曲面逐渐降低,在60°时到达一个低谷,随后角度增大至90°时,透射系数增加,并在α=β=90°时达到一个较高的值。这表明,在三维的图像中取任意垂直于xoy平面的截面,会得到图8类似随角度变化规律的曲线,但三维图像的好处在于能观察到透射系数随两个方向角度同时变化的规律,找出影响最大的变化方向。反射系数的整体变化趋势刚好与透射系数相反,α和β在60°附近时达最大值。
2.2 节理间距
为研究节理间距的影响,固定入射波频率为100 Hz,并取α=β=90°,模拟正入射情况。考虑到之前学者都将节理定义为等间距排列,而实际天然节理分布是越厚的节理分布越稀疏。所以本节定义两条节理间的距离d=ah,h为节理厚度,a为常数,表示为厚度倍数,取值为25~250,即表示节理间距是充填节理厚度的25~250倍。
图12为不同间距倍数a下的透、反射系数随厚度的变化关系。由图12可知,透射系数随节理间距的增大而减小。当a为25~100时,透射系数随节理厚度的增大而增大,且随厚度近似成直线变化,可见在a较小时,厚度为影响透射系数的主要因素。当a为150~250时,此时透射系数随节理厚度的增加而减小趋势变缓。当节理厚度在2~6 mm时,透射系数随a的影响较小,在节理厚度大于6 mm后,透射系数随a增加而增加,表明节理间距a在节理厚度较大时,对透射、反射系数影响较大。这因为在较小的a时,节理的厚度发生变化时,节理间距随a的影响较小,故此时入射波在节理之间传播的能量耗散较小,但在传播至不同厚度的节理时发生的透反射的影响较大;当a较大时,节理间距取代厚度成为影响透反射波幅的主要因素。
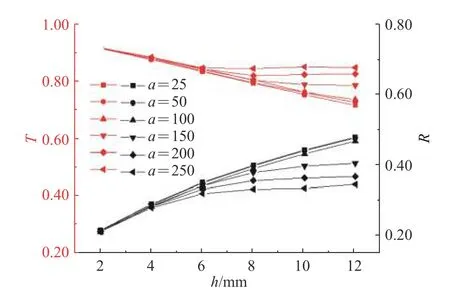
图12 不同间距倍数下的透射、反射系数Fig. 12 Transmission and reflection coefficients at different spacing multiples
2.3 节理数目
由于2.2节中定义的节理间距是节理厚度的线性函数,所以当节理厚度较大时,节理间的距离也相应增大。该节理设定与实际节理的分布相似,即厚度较大或长度较长的节理分布较稀疏。图13和14分别显示了在不同节理厚度下,透射、反射系数随节理数目N的变化。观察图13可以发现,在节理数目N增加时,透射系数先明显降低,随后减小变缓;在节理厚度较小时,透射系数随N变化较大,随着节理厚度的逐渐增加,透射系数随N的变化减小。反射系数先增大,随后基本不变。且当节理厚度增大时,节理数目对透射系数和反射系数的影响逐渐变小。

图13 不同节理数目下的透射系数Fig. 13 Transmission coefficient under different joint numbers

图14 不同节理数目下的反射系数Fig. 14 Reflection coefficient under different joint numbers
观察图13和14可以发现,图中所有曲线的散点分布在一条曲线的一侧,定义这条包络线为临界透射、反射曲线。提取关键数据点,通过数据拟合,得到相应的临界透射、反射曲线表达式为:
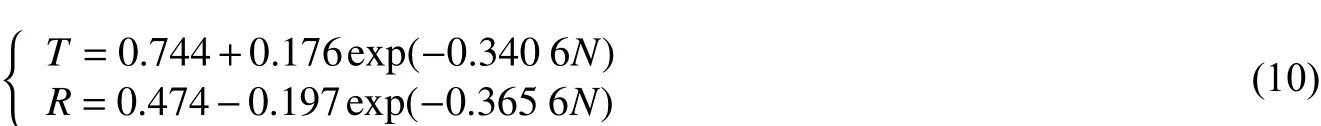
临界透射曲线的实际物理意义为在天然岩体中,若存在充填节理,其分布规律为节理间距与节理厚度之间有正比关系,那么当应力波透过多个节理传播时,不论节理厚度如何变化,其透射系数都在临界透射曲线上方。这表明,在实际岩体中,即使充填节理的厚度出现离散性,得到节理数目后,临界透射曲线上与节理数目对应点的纵坐标值即为透射系数的最小值。临界反射曲线也可看成应力波通过上述岩体的反射系数总在曲线下方,在此不再赘述。
2.4 透射波频率
为研究入射波频率的变化对透射系数的影响,采用单个节理,α=β=90°,厚度在2~12 mm之间变化,频率取值为10、50、100、200、400 Hz,研究不同厚度节理对应力波透射与反射的影响。
图15表示在不同节理厚度下透射、反射系数随频率的变化关系。由图15可知,频率从10 Hz增大到400 Hz时,透射系数整体上逐渐减小。在频率小于100 Hz时,透射系数随节理厚度变化缓慢下降;当入射波频率为200 Hz和400 Hz时,透射系数对厚度的变化很敏感,入射波频率为400 Hz时,当节理厚度从2 mm增至12 mm时,透射系数从0.535 1减至0.284 2。相似的,反射系数随入射波频率的增大而增大,同样在节理厚度较大时影响越明显。上述发现表明高频波通过节理传播越来越困难,充填节理同样也具有滤波作用。在频率相同时,厚度越大的节理对应力波传播的阻碍越明显,反射的能量越大。
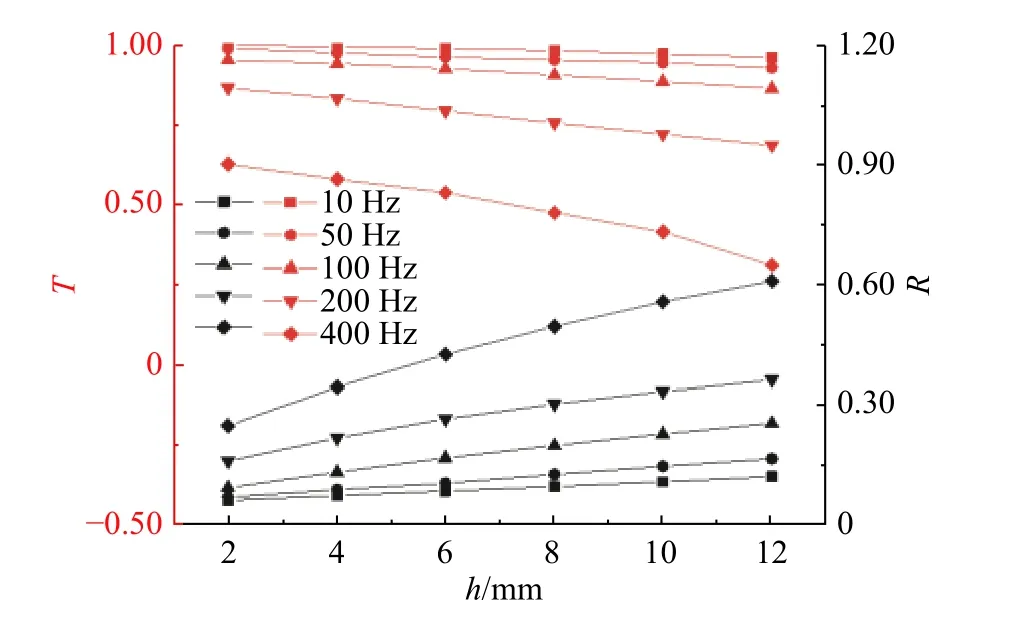
图15 不同厚度下的透射、反射系数随频率的变化Fig. 15 The transmission and reflection coefficients vary with frequency at different thicknesses
3 结 语
(1)在只改变节理视倾角α时,在0°~60°时透射系数随α增大而逐渐减小,在60°~90°时随α增大而增大;反射系数则相反。当节理视倾角α与倾向方位角β相等时,得到的透(反)射系数随α、β变化的曲面在此方向上的梯度最大。
(2)若定义节理间距与厚度的正比关系,则透射系数随节理间距的增加而增加,反射系数反之。根据不同节理厚度下的节理数目与透(反)射系数关系曲线特征,定义其包络线为临界透(反)射曲线,其意义为:当充填节理间距与厚度成正比时,不论节理厚度或间距如何变化,其透(反)射系数均在临界透(反)射曲线上方(下方)。
(3)当入射波频率发生变化时,透射系数随其增大而减小,反射系数则相反,且在节理厚度较大时影响越明显。表明高频波通过节理传播越来越困难,且在相同频率下厚度越大的节理对应力波传播的阻碍越明显。
