考虑倾角的土质边坡Green-Ampt改进入渗模型

雷文凯，董宏源，陈 攀，吕海波, ，梅国雄

(1. 广西大学 土木建筑工程学院，广西 南宁 530004；2. 贺州学院，广西 贺州 542899)

对于土质边坡的降雨入渗，很多学者采用简化的降雨入渗模型来预测坡体的入渗特征[1]，通过基质吸力和重度的变化情况分析边坡的稳定性，其中应用较多的为Green-Ampt入渗模型。经典Green-Ampt入渗模型（简称为GA模型）[2]常用于研究均质土在水平面上的积水入渗，为突破其在地形条件上的应用限制，Chen等[3]对该模型作了扩展，分析了有相同水平投影长度、不同倾角的斜坡在稳定和非稳定降雨时的坡体入渗过程及坡角对降雨入渗、边坡稳定性的影响。Zhang等[4]、常金源等[5]分别运用Chen等提出的扩展模型探讨了边坡在降雨时的浅层稳定性。简文星等[6]在Chen的扩展模型基础上推导出不同雨强下土体的降雨入渗模型。汪丁建等[7]、马世国等[8]分别弥补了传统GA模型在坡长限制、入渗阶段划分方面的不足。

上述研究拓展了传统GA模型的应用范围，但在模型假设中均认为湿润锋至入渗坡面间的土体为完全饱和状态，与实际情形不符[9-10]。张杰等[11-12]假定入渗过程中坡体按含水率分为饱和层、过渡层和未湿润层，推导了入渗深度与降雨时间的关系，但忽略了边坡倾角的影响。基于此，本文在传统Green-Ampt入渗模型基础上提出一种考虑倾角的土质边坡分层假定入渗模型，推导湿润锋推进深度与降雨历时的关系，并通过某边坡降雨入渗实例，将本模型与传统GA模型的计算结果进行对比分析。

1 入渗模型

1.1 传统Green-Ampt入渗模型

对强度大于土体饱和渗透系数的降雨，入渗过程可分为两个阶段[13]：入渗初始阶段，土体入渗能力比降雨强度大，为自由入渗，入渗边界由降雨强度控制，记为阶段Ⅰ；随着降雨进行，土体入渗能力比降雨强度小，转为积水入渗，入渗边界由土体入渗能力控制，记为阶段Ⅱ。设阶段Ⅰ经历时间后转为阶段Ⅱ时刻湿润锋深度为。

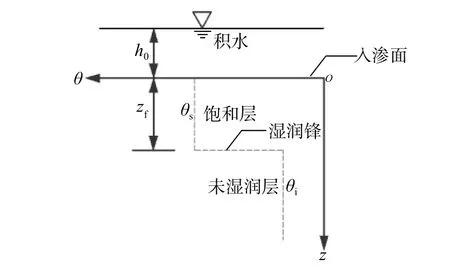
图1 Green-Ampt入渗模型示意Fig. 1 Green-Ampt infiltration model

阶段Ⅰ湿润锋深度与入渗时间的关系为:

式中：ks为土体饱和渗透系数；

式(1)、(2)即为传统Green-Ampt入渗模型的控制方程，其形式简单，求解方便，但没有考虑倾角及非饱和区的影响，如直接用于分析倾斜状的边坡入渗，与实际情况偏差较大。

1.2 考虑倾角的分层假定入渗模型

考虑倾角的分层假定入渗模型如图2所示，该模型假设条件如下：（1）土体是均质的；（2）降雨入渗时土体按含水率划分为饱和层、过渡层和未湿润层，饱和层和过渡层统称为湿润层，两者厚度各占湿润层的一半，通过近似椭圆形曲线来反映过渡层含水率的分布规律，其中椭圆的方向半轴长度为饱和含水率与初始含水率之差，方向半轴长度为过渡层厚度；（3）饱和层水流入渗除受压力势、重力势作用外，还受过渡层吸力势作用。

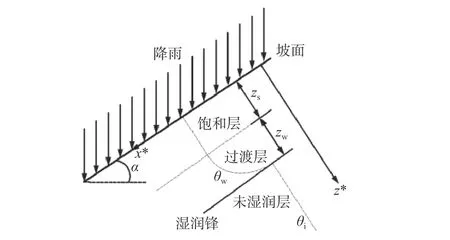
图2 考虑倾角的分层假定降雨入渗模型示意Fig. 2 Stratified assumption model considering inclination

基于上述分析，对累计入渗量作如下修正：

饱和层：Is=(θs−θi)zf/2

过渡层：累计入渗量为1/4椭圆面积。

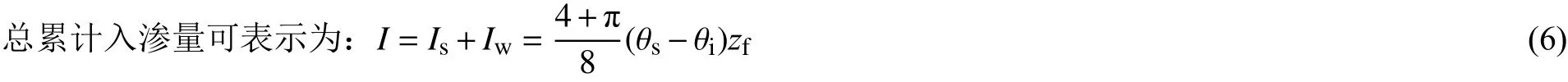
另一方面，根据总累计入渗量与入渗时间的关系，得：

式中：i为入渗速率。

式(11)、(15)为分层假定入渗模型的控制方程，考虑了倾角及非饱和区的影响，更适用于分析倾斜状边坡的入渗。

2 入渗分析

2.1 入渗实例

入渗试验边坡位于南昆铁路百色段那容线路所附近，为黏土堑坡。试验坡段宽2.5 m，斜坡面长6 m，倾角为30°。距坡表3 cm深度处土体的物理性质参数为：天然密度2.12 g/cm3，含水率11.99%，相对密度为2.72，液限为46.4%，塑限为25.8%，饱和渗透系数为3.37×10−7m/s，小于0.005 mm粒径含量56.6%。土水特征曲线如图3所示。

入渗试验在人工模拟降雨条件下进行。人工模拟降雨装置由潜水泵、过滤器、喷头、压力表和水管等组成。喷头均布于坡面，距坡面垂直距离为2 m，本试验降雨强度为25 mm/h，降雨持续时间为10 h。在坡中位置距坡面垂直方向深度为10、20和30 cm处分别埋设1个TDR土壤体积含水率传感器。HOBO数据采集仪与TDR传感器相连，每隔30 s自动记录1次数据。试验观察发现，坡面发生径流时降雨持续的时间为86 min。整理TDR数据，得到不同深度处土的体积含水率随降雨历时的变化见图4。

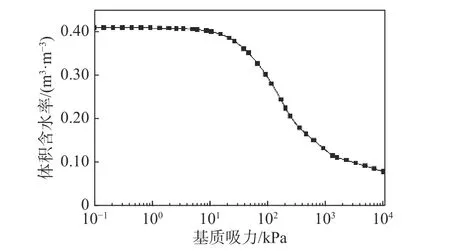
图3 边坡土体土水特征曲线Fig. 3 Water characteristic curve of slope soil

图4 边坡土体的体积含水率变化曲线Fig. 4 Change curve of soil volume moisture content

从图4可以看出，TDR传感器一旦响应后，该深度处土体体积含水率随降雨的持续逐渐增大，直至饱和。该边坡土体初始体积含水率平均值为，饱和体积含水率为。各深度处土体含水率从初始状态增至饱和状态并非在一瞬间完成，而是需要经历一定的过程。

2.2 入渗模型对比分析

根据前述分层假定入渗模型得到计算结果，并与传统GA模型进行对比。该实例中土体的=1.5 m，=1.2 m。根据前文计算式，得出两种模型计算的湿润峰深度随降雨持续时间变化曲线，如图5所示。

分层假定模型与GA模型的湿润锋扩展深度在开始阶段很吻合，但随着入渗的继续，超过75 min后，在同一时刻，分层假定模型湿润锋抵达深度开始大于传统GA模型，且差值越来越大。根据湿润锋抵达10、20和30 cm深度的时间，将两种模型计算值与入渗试验实测值进行对比，见表1。可见，分层假定模型计算值与实测数据吻合度较高。分层假定模型比实测值只略微偏高，最大值偏差约15 min。但GA模型与实测值偏差较大，且随着深度增加偏差越大。

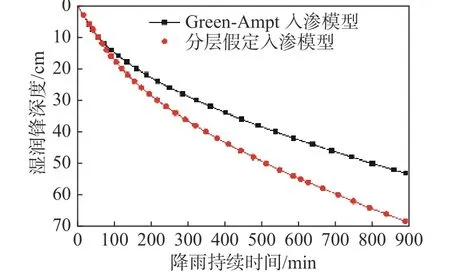
图5 湿润锋深度变化曲线Fig. 5 Variation curve of wetting front depth

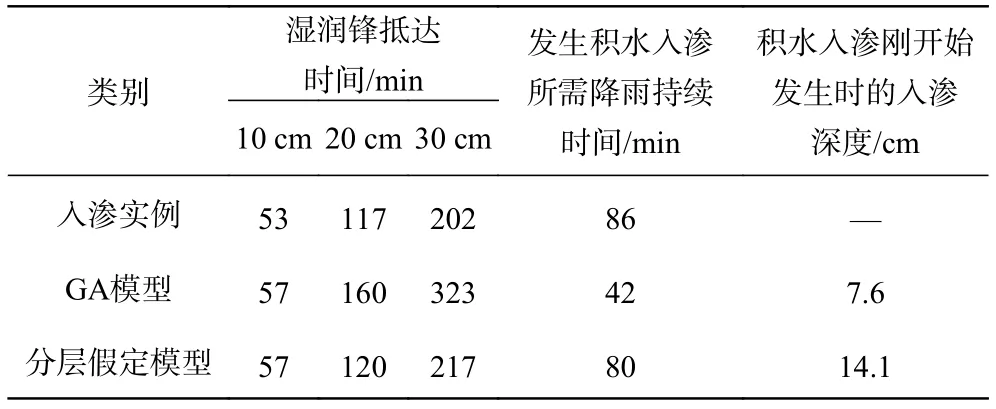
表1 模型计算值与实测值统计Tab. 1 Statistics of calculated and measured values of the model

图6为边坡入渗速率随降雨时间的变化曲线。在自由入渗阶段，入渗速率保持不变；刚进入积水入渗阶段时，入渗速率下降较快，后逐渐变缓。从图6可知：在自由入渗阶段，分层假定模型的入渗速率较GA模型低，且差值基本保持在3 mm/h左右，到达积水入渗阶段后，分层假定模型的入渗速率较GA模型高，两者差值随入渗过程的持续逐渐减小。分层假定模型与GA模型计算出的发生积水入渗所需降雨持续时间分别为42和80 min。GA模型较实测值偏低29 min，而分层假定模型仅比实测值偏低6 min。GA模型计算出的积水入渗刚开始发生时的入渗深度明显小于分层假定模型，几乎为后者的一半。

两种模型表现出差异的主要原因有两个：(1)分层假定模型考虑了非饱和区的影响，对累计入渗量作了修正；(2)分层假定模型水流入渗路径为zf/2，将非饱和层平均基质吸力水头视为作用在饱和层上的基质势，并考虑了倾角的影响，从而对传统GA模型的入渗水力梯度作了修正。

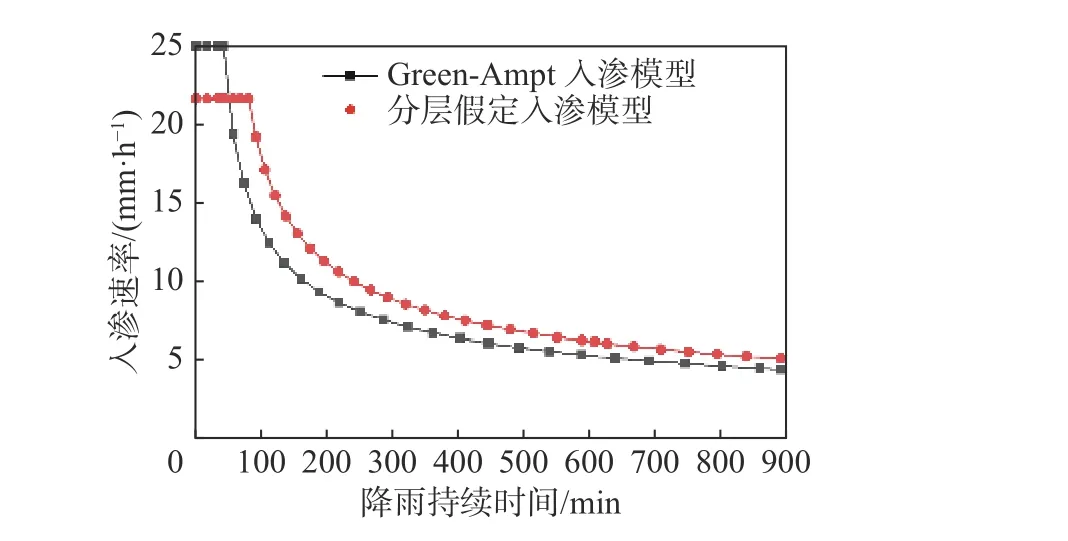
图6 边坡入渗速率随降雨持续时间的变化曲线Fig. 6 Change curve of infiltration rate of slope

2.3 倾角、雨强和土体渗透系数对边坡降雨入渗的影响

边坡倾角影响了雨水沿坡面垂直方向的重力势能梯度及边坡单位面积上的受雨量，在相同的土体参数和降雨条件下，倾角越大，边坡单位面积上的受雨量及雨水的入渗势能梯度均越小。当土体饱和渗透系数取值3.37×10−7m/s，雨强取值25 mm/h时，不同倾角条件下边坡降雨入渗深度随降雨历时的变化曲面如图7所示。可见，随着边坡倾角的增大，雨水入渗到坡体内相同深度所需的降雨历时增加，这种现象在倾角大于60°时更为明显。倾角超过60°时，随着倾角增大，坡面单位面积受雨量和雨水入渗势能梯度降低的幅度大大增加，雨水在边坡中入渗变得更加困难。

雨强影响了边坡单位面积上的受雨量，从而影响边坡土体入渗。当土体饱和渗透系数取值3.37×10−7m/s，边坡倾角为30°时，不同雨强下边坡降雨入渗深度随降雨历时的变化曲面如图8所示。可见，随着雨强的增大，雨水入渗到坡体内相同深度所需的降雨历时减小，这种现象在雨强小于20 mm/h时尤为明显。雨强超过20 mm/h后，继续提高雨强对边坡降雨入渗的影响不大。由2.2中分析可知：自由入渗阶段，雨水在边坡上的入渗速率由雨强决定；在积水入渗阶段，雨水在边坡上的入渗速率受边坡土体的入渗能力控制，与雨强无关。因此，雨强主要通过影响边坡积水入渗发生的时间来影响边坡的降雨入渗深度-降雨历时关系。

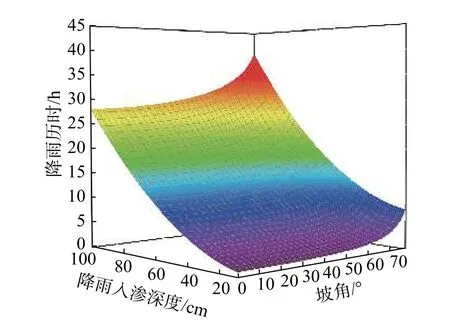
图7 不同倾角下边坡降雨入渗深度随降雨历时的变化（雨强为25 mm/h）Fig. 7 Change surface of different rainfall infiltration depths with rainfall duration under different slope angles(Rainfall intensity is 25 mm/h)

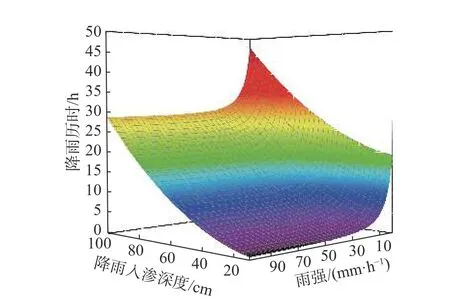
图8 不同雨强下边坡降雨入渗深度随降雨历时的变化（边坡倾角为30°）Fig. 8 Change surface of different rainfall infiltration depths with rainfall duration under different rainfall intensities(Slope angle is 30°)

当边坡倾角为30°、雨强取值25 mm/h时，不同土体渗透系数下边坡降雨入渗深度随降雨历时的变化曲面如图9所示。可见，随着土体渗透系数的减小，雨水入渗到坡体内相同深度所需的降雨历时增大，这种现象在降雨入渗深度超过30 cm时逐渐变得明显。土体渗透系数对边坡降雨入渗的影响随深度的增加变得更为显著。

图9 不同土体渗透系数下边坡降雨入渗深度随降雨历时的变化（边坡倾角为30°、雨强为25 mm/h）Fig. 9 Change surface of different rainfall infiltration depths with rainfall duration under different soil permeability coefficients (Slope angle is 30°, and rainfall intensity is 25 mm/h)

3 结 语

(1)考虑倾角的分层假定模型预测的湿润锋深度与降雨时间的关系较传统GA模型更接近入渗试验的监测值，准确性更高。在自由入渗的时间段内，两种模型湿润锋扩展趋势保持一致；之后，相同入渗时间，分层假定模型的湿润锋扩展深度较GA模型大。

(2)在入渗初期，两种模型湿润锋扩展速度较快，分层假定模型的入渗速率较GA模型小；到达积水入渗阶段后，湿润锋运移速度有下降趋势，两种模型的入渗速率迅速降低。在同一入渗深度或入渗时间处，分层假定模型的入渗速率都比GA模型大，这种差异随着入渗的持续逐渐变小。

(3)利用考虑倾角的分层假定入渗模型，可以方便快速地分析倾角、降雨强度等参数对边坡降雨入渗的影响。随着边坡倾角的增大，雨水入渗到坡体内相同深度所需的降雨历时增加；随着雨强的增大，边坡湿润锋扩展的速度加快。并且，这些参数有临界值，超过临界值后，对边坡降雨入渗的影响作用发生突变。