配筋率对混凝土Ⅰ-Ⅱ复合型断裂过程声发射特征的影响

巩妮娜 ，胡少伟, ，范向前，蔡小宁

(1. 江苏海洋大学 土木与港海工程学院，江苏 连云港 222005；2. 河海大学 力学与材料学院，江苏 南京 210098；3. 南京水利科学研究院，江苏 南京 210029)

混凝土结构中的裂缝通常处于复杂应力场中，Ⅰ-Ⅱ复合型裂缝是出现最为广泛、需要迫切解决的断裂形式[1]。声发射技术是根据材料内部产生的瞬时弹性波来判断损伤程度的一种检测方法，可用于混凝土断裂全过程的连续监测[2]。在混凝土Ⅰ型断裂研究的基础上，国内外学者对Ⅰ-Ⅱ复合型断裂进行了试验与理论研究。Jenq等[3]建立模型描述Ⅰ-Ⅱ复合型断裂行为，分析起裂角、裂缝扩展路径等断裂性能，并采用直偏裂缝三点弯曲梁试验加以验证。董伟等[4,1]通过四点剪切梁试验建立了Ⅰ-Ⅱ复合型裂缝起裂准则，并分析初始条件对断裂性能的影响。胡宗棋[5]基于Ⅴ型切口试件研究混凝土复合型断裂行为，得到断裂参数与切口角度等的关系，并指出广义应变能密度准则能够更加精准地描述断裂行为。韩金启等[6]将损伤理论引入断裂问题分析中，推导出I-II复合型裂缝缝端微裂纹区临界区域公式，描述混凝土损伤断裂过程。Jacobsen等[7]采用双边切口的棱柱体试件研究混凝土复合型断裂行为，分析了应力及扩展路径的发展过程。García-álvarez等[8]提出了一个基于非线性断裂力学的类脆性材料裂纹扩展模型，可模拟高强及普通混凝土复合型断裂行为。Ayatollahi等[9]提出了修正的应变能密度准则以分析混凝土Ⅰ-Ⅱ复合型断裂性能，其结果与试验吻合较好。Carmona等[10]基于三点弯曲梁分析了不同初始条件下钢筋混凝土I-II复合型断裂参数的变化规律，发现钢筋的存在不仅影响临界荷载，还能改变断裂模式。

近年来声发射技术逐渐应用于断裂力学领域，已有研究证明特定声发射参量能够反映裂缝扩展过程，并可对裂缝发展进行监测和评估。Hu等[11]通过试验发现，声发射参量可较为准确地判断试件起裂及失稳临界时刻，与累积损伤密切相关，构建了不同混凝土的损伤演化关系。Saliba等[12-14]建立了声发射参量与初始缝高比、断裂能等参数之间的关系。张璇子等[15]采用声发射参量描述混凝土材料所处应力水平，动态预报不同应力水平下的损伤程度。胡钰泉等[16]指出在变幅循环荷载作用下，带裂缝混凝土表现出明显的声发射Kaiser效应，这一效应本质上取决于混凝土内部损伤程度。Zaki等[17]采用声发射技术监测和评估腐蚀环境下钢筋混凝土梁的力学行为，并基于RA、AF等参量的变化对试件破坏过程进行分级。

现有研究多集中在混凝土的断裂性能和声发射特征，钢筋混凝土Ⅰ-Ⅱ复合型断裂行为的研究成果较少，因此，本文基于直偏裂缝三点弯曲梁，研究不同配筋率下混凝土Ⅰ-Ⅱ复合型断裂过程及声发射特征。

1 试验概况

为研究不同配筋率下混凝土I-II复合型断裂性能及声发射特性，参考《水工混凝土断裂试验规程》（DL/T 5332—2005），设计4组直偏裂缝钢筋混凝土三点弯曲梁（见图1），尺寸为1 000 mm×200 mm×120 mm，初始缝高比取0.4，预制裂缝与试件跨中的水平距离取160 mm，即偏移比d= 160/400= 0.4。混凝土组成材料为P·O 42.5水泥、大石（粒径为16.5～31.5 mm）、小石（粒径为5.0～16.5 mm）、机制砂、水、粉煤灰和高性能减水剂。质量配合比为：m水∶m水泥∶m砂∶m大石∶m小石∶m粉煤灰∶m减水剂=0.37∶1.00∶2.95∶2.72∶0.69∶0.20∶0.02。梁底部配置HPB300的纵向光圆钢筋，保护层取25 mm，各参数如表1所示，配筋率按文献[10]方法计算。

图1 钢筋混凝土试件示意（单位: mm）Fig. 1 Schematic of reinforced concrete specimen (unit: mm)

表1 试件配筋参数Tab. 1 Reinforcement parameters of specimens

本次试验均在1 000 kN电液伺服结构试验系统上进行，采用位移控制加载，同时通过SENSOR HIGHWAY Ⅱ型声发射系统同步采集断裂全过程的声发射信号，试件表面布设4个传感器（见图1）。试验前在预制裂尖左右两侧对称布设两个应变片，裂尖与加载点间连一直线，垂直于直线布设1组应变片，监测起裂荷载及裂缝扩展情况，由于复合型断裂试验在跨中亦可能出现开裂现象，本文在跨中底部布设2个应变片监测此处开裂（见图2）。数据采集系统为DH3818型采集器，主要采集数据包括：荷载P、裂缝张开口位移（DCMO）、各应变片应变值ε等。其中荷载通过加载位置的荷载传感器测量，张开口位移DCMO采用标距12 mm、测量范围−1～4 mm的夹式引伸计测量。声发射门槛值取30 dB，前置增益取40 dB，模拟滤波器上限取1 MHz。

图2 试验加载装置Fig. 2 Test loading device

2 试验结果分析

2.1 配筋率对临界荷载的影响

观察试验现象可知，钢筋的加入使得钢筋混凝土Ⅰ-Ⅱ复合型断裂过程与素混凝土有较大差异。图3为试验测得RC01试件的P-DCMO曲线。由图3可见：①在加载初期，即图中O至A点，裂缝张开口位移DCMO随荷载P基本呈线性增加趋势，即线弹性特点；②从A至B点，P-DCMO曲线表现出了明显的非线性特征，裂缝缓慢、稳定扩展，荷载值P由23.64 kN小幅增至26.95 kN，随后试件开始失稳扩展，本文定义B点对应的荷载为失稳荷载Pu；③进入失稳扩展阶段后，与素混凝土梁的脆性特征不同，钢筋混凝土试件的P-DCMO曲线缓慢下降，张开口位移与加载点位移迅速增加，荷载值缓慢减小，甚至出现小幅增长的现象，但最终最大荷载与失稳荷载数值差别不大，在到达失稳荷载后钢筋混凝土试件表现出了明显的延性特征，文献[10,18]亦得到了类似的结论。

图4给出了4组不同配筋率试件的失稳荷载Pu平均值随配筋率ρ的变化规律。由图4可知，失稳荷载Pu平均值与配筋率ρ近似呈现线性关系，在加载初期，构件的主要受载体为混凝土，钢筋未起到关键性作用，随着加载的进行钢筋作用逐渐明显，因此，随着配筋率ρ的增加，起裂荷载并未表现出单调增加的趋势，但试验结果表明失稳荷载Pu逐渐增加，即保证构件正常工作的承载能力得到提升，配筋率ρ的增加可有效提高试件抵抗失稳破坏的能力。

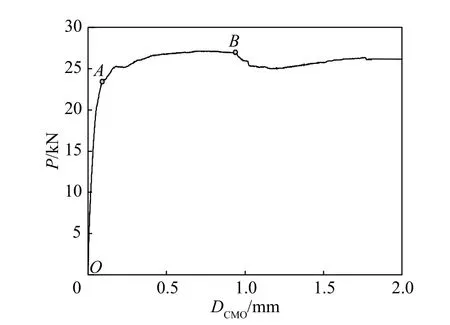
图3 P- DCMO（RC01）Fig. 3 P- DCMO curve for RC01

图4 失稳荷载随配筋率变化曲线Fig. 4 Curves of unstable load versus reinforcement ratio

2.2 配筋率对裂缝扩展路径的影响

图5 为试验所得不同配筋率试件的裂缝扩展路径，其中RC03跨中处有1条裂缝用椭圆线条标出。由图5可知，随着配筋率ρ的增大，最终扩展路径由起始于裂尖的复合型斜裂缝逐渐过渡到斜裂缝与临近跨中的弯曲型裂缝同时存在，再到仅有临近跨中弯曲型裂缝，这是由于钢筋的存在对预制裂缝有限制作用。随着配筋率ρ的增大，限裂作用增强[18]。因此，裂尖附近区域的微裂缝产生、汇集减少，同时临近跨中底部的危险程度相对更大，最终临近跨中位置形成贯通的弯曲型裂缝，即配筋率影响裂缝扩展模式。同时，根据纵向配筋率及试件几何形状的不同，钢筋周围的混凝土可能无法抵抗钢筋传递的剪力，因此钢筋所在位置处的混凝土会出现裂缝，如图5中RC02～RC04所示，这与文献[10]结论一致。需要说明的是，跨中底部没有预设裂缝，试验中跨中开裂的位置并未严格出现在试件对称轴上，而是在临近跨中的一个区域内向加载点发展。

图5 不同试件的裂缝扩展路径Fig. 5 Crack propagation paths of different specimens

3 配筋率对试件断裂过程声发射特征的影响

3.1 振铃计数分析

声发射振铃计数是指越过门槛信号的振荡脉冲数，在一定程度上反映了声发射信号的幅度，对于连续性信号的测量具有重要意义[2]。不同配筋率试件断裂全过程的荷载与振铃计数时程曲线如图6所示。

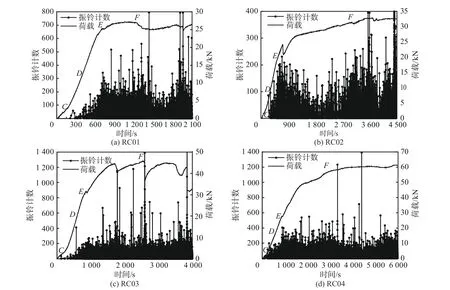
图6 不同配筋率试件荷载与振铃计数时程曲线Fig. 6 Time-history curves of load and AE ringing counting for specimens with different reinforcement ratios

分析图6可得出以下结论：

（1）从试件初始加载到裂尖起裂的CD阶段，能够统计到的振铃计数数值及数量均较少，在裂尖起裂时刻即D点，振铃计数有小幅突变，邻近其他时刻也有多次信号跃迁。这是由于在加载初期材料裂隙逐渐压密，导致测得超过门槛的振荡次数较少；同时试件在裂尖和其他薄弱部位都会萌生少量微裂缝，因此起裂时刻的峰值并不明显，这与文献[19]描述一致。在跨中底部开裂和失稳临界状态即图6中的E点和F点，振铃计数有相对明显的突变，且在EF阶段出现了若干次数值接近的峰值振铃计数。这是由于在裂缝稳定扩展过程中，混凝土韧带处开裂，部分荷载转移至钢筋，随后微裂缝继续萌生、扩展，混凝土与钢筋交替承载，不断地达到新的平衡。进入失稳扩展阶段即F点后，宏观裂缝快速发展，逐渐形成贯通裂纹，声发射信号活动性增强，超过门槛的振荡次数和强度增大，振铃计数会出现多次突增，其数值甚至超出稳定扩展阶段的最大值。因此，可以将出现若干次数值接近的峰值振铃计数作为临近失稳扩展的标识提前预警，这一特点对于混凝土结构健康监测具有现实意义。

（2）RC01的裂尖起裂及失稳临界状态所对应的时刻分别为445和1 257 s，即稳定扩展持续812 s，而RC02、RC03、RC04试件的稳定扩展时间分别2 712、1 984和2 322 s。这是由于随着配筋率ρ的增大，钢筋承载能力增强，混凝土与钢筋交替承载不断形成新的平衡，循环次数增多，过程增长，从试验现象来看，当配筋率时（即RC02～RC04），临近跨中开裂并逐渐形成宏观贯通裂缝，如图5所示。这一弯曲型裂缝的扩展也在释放能量，导致稳定扩展历时变长，延性增强。因此，可取0.327%作为配筋率ρ的临界点，小于此值失稳扩展出现更突然。这一结论可为结构预警系统建立提供参考依据。

3.2 累计计数分析

累计计数是指在声发射过程中，某一声发射特征量的累计值，从整体上描述了声发射总强度，是材料内部结构变化累加效果的外部表现。声发射能量是与信号幅度及幅度分布相关的参量，虽然不是物理意义上的能量，但对衡量和评价材料的断裂及损伤程度有重要意义[2]。撞击数为超过门槛并使某一系统通道获取数据的任意声发射信号。本文采用累计振铃计数、累计能量和累计撞击数，结合荷载时程曲线分析钢筋混凝土Ⅰ-Ⅱ复合型断裂全过程，如图7所示。

图7 不同配筋率试件累计计数与荷载时程曲线Fig. 7 Time-history curves of load and cumulative counts for specimens with different reinforcement ratios

分析图7可知：

（1）从试件加载初期的压密与弹性变形至裂尖开裂阶段即CD段，微裂缝逐渐萌生，声发射信号强度和频度很小，累计计数均保持较小数值且没有明显变化；从裂尖起裂时刻至跨中开裂时刻即DE段，裂尖周围区域的微裂纹产生、发展并集中，出现较前一阶段更多更强的声发射信号，在E点处出现累计振铃计数、能量及撞击数第1次明显突变；从跨中开裂至失稳临界状态即EF段，虽然试件跨中底部无剪力但承受最大弯矩Mmax。因此出现2个薄弱部位，即裂尖和跨中底部；2个区域附近的微裂缝进一步扩展、汇集。同时混凝土和钢筋交替承载，并且钢筋所在位置的混凝土无法承受钢筋传递的剪力，可能出现新的宏观裂缝。这些都导致EF阶段声发射信号强度和频度显著增强，最终在稳定扩展的终点即F点，累计振铃计数、能量及撞击数再次出现明显突变；进入失稳扩展阶段即F点后，贯通裂缝出现，裂缝宽度显著增加并快速向加载点发展，试验现象如图5所示。声发射信号明显增强，甚至出现远超稳定扩展的峰值信号，累计计数快速增长并且可能再次出现突变（如图7），最终构件丧失承载能力破坏。

从图7的突变点可知，在跨中开裂和失稳临界状态时，累计振铃计数、累计能量及累计撞击数均有明显突增，因此这3个参数的突变可以作为Ⅰ-Ⅱ复合型断裂过程中跨中开裂和失稳临界状态的识别特征。在断裂全过程中，累计振铃计数、累计能量及累计撞击数具有基本一致的变化趋势和突变幅度，说明这3个参数具有较强的相关性，在一个声发射事件中基本呈正比关系。

（2）当配筋率ρ取0.419%和0.654%时（即RC03和RC04），累计撞击数分别约为90 000和70 000次，远超RC01和RC02的累计撞击数，分析原因在于，随着配筋率ρ的增加，混凝土与钢筋间的交替承载作用更强，随之声发射活动强度和频度增加，超过门槛的撞击数显著增加。特别地，对于试件RC02，试验采用了1根ϕ10的钢筋，虽然其配筋率ρ相比RC01有所增大，但钢筋根数减少，导致混凝土与钢筋交替承载频度减弱，且包裹在钢筋周围的混凝土开裂的情况减轻，因此声发射信号相对减少。这也解释了RC02的振铃计数、能量及撞击数相对RC01均有一定程度的减少，见图6（b）和图7（b）。这一现象说明纵向钢筋布设根数对于试件断裂过程中的声发射信号也会产生影响，该问题有待下一步进行深入探讨。

3.3 失稳扩展前声发射信号频率特征分析

不同材料、不同状态或开裂过程所发出的声发射信号频率不同。因此本文对不同配筋率的钢筋混凝土试件Ⅰ-Ⅱ复合型断裂过程的声发射峰频进行统计分析，得到峰频-时间分布图（见图8）。

图8 不同配筋率试件的峰频-时间分布Fig. 8 Peak frequency-time distribution for specimens with different reinforcement ratios

由于受载试件失稳破坏前的声发射活动较为剧烈，为了研究其频谱随加载及损伤过程的变化情况，分析失稳状态前不同荷载水平下试件的声发射峰频特性，结合失稳状态前的荷载-时间曲线，定义荷载水平，其中：P为某一时刻试件承受荷载（kN）；Pu为试件的失稳荷载（kN）。选取70%荷载水平至失稳荷载Pu作为分析峰值频率变化规律的时间区间，不同配筋率试件失稳扩展前的优势峰频占比-荷载水平变化曲线见图9，研究优势频段分布及所占比例[20]。其中将70%～75%荷载水平区间统计所得优势峰频占比记作75%荷载水平的对应值。

图9 不同配筋率的试件失稳前优势峰频分布Fig. 9 Dominant peak frequency distribution ratio before unstable propagation for specimens with different reinforcement ratios

此外，为了研究失稳临界状态前声发射信号峰频的分布变化，选取85%～100%荷载水平区间，相同的峰频数值按1次计，统计不同荷载水平下出现的峰频数量[20]，其中将80%～85%荷载水平区间的统计值计为85%荷载水平的对应值，如表2所示。

分析图8、图9及表2，得出以下结论：

（1）根据图8可知，不同配筋率的试件在I-II复合型断裂过程中，声发射峰频点均呈现分频段集中的现象。随着加载时间的增加，峰频密集带由初始的30～45 kHz、140～155 kHz向 10～25 kHz、30～60 kHz、140～155 kHz过渡，优势峰频点有所增加并趋于稠密。结合荷载时程曲线可知，裂缝稳定扩展阶段的峰频点分布更分散。各试件的峰频点基本集中在170 kHz以下，极少量的数据点出现在250 kHz附近。在配筋率时（即RC03，RC04），除了优势频段外，其他峰频值的数量增多，峰频点分布更为杂乱，即频率成分更加分散。

表2 不同配筋率试件失稳前峰频数量统计Tab. 2 Number of peak frequencies before unstable propagation for specimens with different reinforcement ratios

（2）分析图9可知，随着配筋率ρ的增加，在达到失稳临界状态即100%荷载水平前，140～155 kHz频段的占比从10%增至30%左右，同时45～60 kHz的频段占比明显减小，从30%降至5%以内。当配筋率ρ为0.277%时（即RC01），超过80%荷载水平后，优势频段主要集中在30～60 kHz，其中以30～45 kHz占比最多，约为 50%。当配筋率 ρ ≥0.327%时（即 RC02～RC04），优势频段为 30～45 kHz和 140～155 kHz，即随着配筋率ρ的增大，中高频段的声发射信号明显增加，低频段中45～60 kHz的信号基本消失。配筋率ρ取0.327%可视为转折点。

（3）从图9可知，对于不同配筋率的试件，10～25 kHz的峰频区间占比基本保持在5%以内，仅有RC02的个别点达到8%，处于较低水平。从85%荷载水平开始，140～155 kHz频段占比均呈减小趋势，同时30～45 kHz频段占比呈增加趋势，这一特点可为结构失稳状态的提前预警提供参考依据。

（4）由表2可知，各试件荷载水平从95%增至100%的过程中，峰频的数量均有所增长，且RC01和RC03的增长十分明显。说明临近失稳临界状态时，声发射信号峰频分布逐渐分散，小直径钢筋的这种趋势更加明显。

4 结 语

（1）钢筋的加入能够促使直偏裂缝三点弯曲梁发生延性破坏，随着配筋率ρ的增加，试件的失稳荷载Pu呈近似线性增加趋势。配筋率影响混凝土Ⅰ-Ⅱ复合型断裂模式，随着配筋率ρ的增大，宏观裂缝由起始于裂尖的复合型斜裂缝逐渐过渡至临近跨中的弯曲型裂缝。

（2）裂缝稳定扩展过程中混凝土与钢筋之间交替承载，振铃计数出现若干个峰值，累计振铃计数、累计能量及累计撞击数的突变可作为Ⅰ-Ⅱ复合型断裂的跨中开裂和失稳临界状态的识别特征，且3个参数间具有较强的相关性。

（3）不同配筋率的试件在Ⅰ-Ⅱ复合型断裂过程中，声发射峰频点均呈现分频段集中的现象，随着加载的进行，优势峰频点有所增加并趋于稠密。当配筋率 ρ ≥0.327%时，中高频段的声发射信号明显增加，低频段中45～60 kHz的信号基本消失。从85%荷载水平开始，140～155 kHz的频段占比减小，同时30～45 kHz频段占比增加，临近失稳临界状态时峰频分布趋于分散，可作为预测结构失稳破坏的前兆，为混凝土工程预警系统的建立提供依据。