一种求解极大极小问题的灵活非单调滤子方法

苏珂，林雨萌，李小川

(河北大学 数学与信息科学学院，河北省机器学习与计算智能重点实验室，河北 保定 071002)

求解非线性不等式约束优化问题的方法有很多[1-4].在这些方法中，通常使用罚函数或拉格朗日函数来检验迭代的可行性.罚函数法就是通过求解若干个罚函数的极小值来得到约束优化问题的极小点的方法.但是，罚函数的使用，特别是罚参数的选择，存在着一些困难.进而提出了滤子技巧[5]，之后滤子技巧被应用于多种约束优化问题[6-12]，但滤子方法仍不可避免地遇到了Maratos效应.Maratos效应是指价值函数拒绝了一些在解决问题上取得良好结果的试探点.为克服滤子方法的不足，Ulbrich[13]提出了一种以拉格朗日函数代替目标函数作为接受准则的新滤子方法.在此基础上，Nie等[14]利用固定标量将目标函数和约束违反度函数相结合，作为新的目标函数，但试探点的判别准则不变.实际上，如果能够对当前试探点放松接受准则，就可以在一定程度上避免Maratos效应，同时降低计算成本.

基于上述思想和方法，本文提出了一类具有自适应参数的极大极小问题的非单调滤子信赖域方法.与Ulbrich[13]提出的理论不同，本文在滤子中不使用拉格朗日函数，而是使用与文献[14]相似的函数.此外，与Nie[14]等所提出的判别准则不同的是本文中的参数不是固定的，是可以改变的，这意味着判别准则是根据参数的不同而更新的.为了避免试探点落入“山谷”，还在判定中加入了非单调技术.与现有的序列二次规划(SQP)-滤子方法不同，本文修正了二次子问题，使其总是可行的，从而避免了可行性恢复阶段，并在一定程度上减少了计算量.在合理的假设下，该算法具有全局收敛性.

1 一种改进的求解极小极大问题的灵活非单调滤子方法

考虑下面的极大极小最优化问题

(1)

其中fj(j∈I={1,2,…，m})：Rn→R是Rn上连续可微的实值函数.

显然，目标函数φ(x)是连续的，但不一定是可微的.式(1)等价于式(2).

mint

s.t.fj(x)-t≤0,j∈I={1,2,…,m},

(2)

其中(x,t)∈Rn+1，定义

C(x,t)=(f1(x)-t,f2(x)-t,…,fm(x)-t)T,

其雅可比矩阵为A(x,t).

定义指标集如下：IA(x)={j:fj=φ(x),j∈I},IN(x)={j:fj<φ(x),j∈I}.

令

f(x)=(f1(x),f2(x),…,fm(x))T,e=(1,1,…,1)T∈Rm.

构造对角矩阵F(x)=diag(f1(x),f2(x),…,fm(x)).

为了求解式(2)，通过以下二次问题(QP)求得搜索方向dk

(3)

其中Δk是信赖域半径，Hk∈Rn×n是f(x)的二阶近似Hesse阵.

定义约束违反度函数h(x,t)=‖C(x,t)+‖2,其中Cj(x,t)+=max{Cj(x,t),0,j∈I},C(x,t)+=(C1(x,t)+,C2(x,t)+,…,Cm(x,t)+)T.定义目标函数p(x,t)=t，在当前迭代点xk处，令pk=p(xk,tk)，hk=h(xk,tk)，Ck=C(xk,tk).

点对支配定义、滤子集定义和试探点被接受的定义均和文献[9]中定义1、2、3相同.

在经典的滤子方法中，可接受的点对位于(h,p)平面的左下角(图1，区域I),被拒绝的点对位于(h,p)平面右上部分(图1，区域II).

为了避免Maratos效应，设在第k次迭代处的目标函数为

l(xk,tk)=p(xk,tk)+δkh(xk,tk)=p(xk)+δk‖C(xk,tk)+‖2,

(4)

其中，对于j=1,2,…,m,Cj(xk,tk)+=max{Cj(xk,tk),0}，δk是第k次迭代时的一个自适应参数，它可以根据当前试探点的不同改进而改变.设l(xk,tk)=lk，在传统滤子方法中，式(4)中δk=0(图2).图2的右半部分有4个区域I、II、III、IV.在当前迭代k处，若试探点对(hk,lk)进入区域IV，根据接受准则，拒绝该试探点对.若(hk,lk)进入区域I、II或III，则调整参数δk.对于区域III，为了实施更严格的接受准则，增加δk的取值，这将导致拒绝区域变大，接受区域变小(图3).因此，δk的更新为

(5)

图1 经典滤子集示意Fig.1 Schematic diagram of classical filter set

图2 含参数滤子集示意Fig.2 Schematic diagram of filter set with parameters

若(hk,lk)进入区域II，则该算法进行了很好的改进，故放宽接受准则，使接受域变大，即降低δk的值(图4)，所以δk更新为

(6)

若(hk,lk)进入区域I，则接受该点对，且lk增加，hk减小，δk不变.若(hk,lk)进入区域IV，则该点对被拒绝，δk不变.

图3 松弛滤子集示意Fig.3 Schematic diagram of relaxation filter set

图4 严格滤子集示意Fig.4 Schematic diagram of strictly filter set

算法A的描述形式如下：

步骤0令0<Δ0<1,0<γ<β<1,0<λ≤1,0<γ0<γ1≤1<γ2,M≥1,μ>0,α1=α2=0.5，x0∈Rn,H0∈Rn×n是正定矩阵，初始区域半径Δ0≥Δmin>0,F0={(μ,+∞)}.令k=0,m(k)=0 .

步骤1 求子问题QP得到(dk,zk)，如果‖dk‖=0终止.

步骤6 令Δk∈[γ0Δk,γ1Δk]，转步骤1.

2 算法的收敛性

假设下面的条件是成立的.

假设1对于任给的点x0∈Rn，水平集L(x0)={x∈Rn:φ(x)≤φ(x0)}是紧集.

假设2任给的点x∈L(x0)，目标函数梯度向量线性无关.

假设3函数fj和约束函数Cj(j∈I)是二次连续可微的.

假设4对于所有的k,{(xk,tk)}位于Rn的有界闭凸子集S上.

假设5函数A:Rm×(n+1)→Rn+1在定义域上是一致有界的.

假设6序列矩阵{Hk}是一致有界的,即对于所有的k，MH>0，其中‖Hk‖≤MH.

对于所有的{(xk,tk)}∈S，根据上面的假设，存在一个约束Mf使得‖2fj(xk)‖≤Mf,j∈I.可以假设存在一个约束ν1、ν2，使得‖p(xk,tk)‖≤ν1,‖C(xk,tk)‖≤ν2，‖C(xk,tk)‖≤ν2，‖2C(xk,tk)‖≤ν2.问题(2)在点(x*,t*)的Karush-Kuhn-Tucker条件为

引理1假设(dk,zk)是SQP信赖域子问题(3)的解，则

1) 如果dk=0则zk=0;2) 如果dk≠0则zk<0.

证明:1)不失一般性，在式(3)中，根据算法A可知，因为(dk,zk)是SQP信赖域子问题(3)的解，所以存在乘子νk∈Rm和νk∈R，满足

在建筑物受太阳辐射的各个外表面中，屋面是建筑物上部与外界直接接触的重点部位，受辐射热也是最多的，其保温与隔热对建筑节能具有重要意义。为达到节能目的，屋面上可设置架空层增加空气的流动，蓄水屋面及设置屋顶绿化形成生态型屋面等。这样不仅可以增加环境的美观性，还可以改善建筑物屋面的热工性能以达到节能的目的。屋面保温材料的选用上不宜用密度大、导热系数高的材料，这样会导致屋面的重量和厚度过大，不利于结构设计；同时也不宜选用吸水率较大的材料，防止保温层吸水而降低保温效果。

(Hk+νkE)dk+f(xk)νk=0,eTνk=1,

(F(xk)+diag(f1(xk)Tdk,…,fm(xk)Tdk)-(φ(xk)+zk)E)νk=0,uk(‖dk‖-Δk)=0,f(xk)Tdk-zke≤φ(xk)e-f(xk),‖dk‖≤Δk,νk≥0,uk≥0.

如果dk=0，可以得到zk≥0.

引理2假设1～6成立，且令(dk,zk)是子问题(3)的可行点，则

(7)

(8)

证明:对于所有的j∈I，使用Taylor展式可以得到

其中yk介于xk和xk+dk之间.因为dk是可行的且‖2fj(yk)‖2≤dk，得到

|δk+1|<Δk，因此

则式(8)成立.

引理3在假设条件成立前提下，算法A是有效的.

证明:当δk充分小时，证明滤子可以接受试探点(xk+1,tk+1)，考虑下面2种情况.

根据δk的更新和式(8)，可得

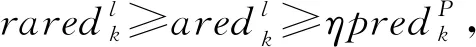
当Δk→0时，得证.

证明:若算法A非有限终止，则有无限多个迭代点被滤子接受.根据滤子的定义，分2种情况证明：

1)因为m(k+1)≤m(k)+1,有

(9)

当n=k+1，分以下2种情况讨论：

定理1设{(xk,tk)}是由算法A生成的无穷序列，则存在{(xk,tk)}的聚点为式(2)的Karush-Kuhn-Tucker点.

因此存在一个子集K，ν*∈Λ使得在K上，νk→ν*.称序列{νk}收敛于ν*.

令IA(x)={j∶νk,j>0},对于任意的j∈IA(x),由引理1中证明可知

fj(xk)Tdk=φ(xk)+zk-fj(xk),

3 数值结果

算法参数设置如下：H0=E∈Rn×n,β=0.6,γ=0.1,Δ=0.5,α=α1=α2=0.45,η=η1=η2=0.25,程序用Matlab编写.

解为x=(1.139 0,0.899 6)T,f1=f2=1.952 2.初始点是x0=(1,-1)T.

解为x=(1,1)T,f1=f2=f3=2.初始点是x0=(1,-1)T.

解为x=(0.453 3,-0.906 6)T,f1=f3=0.616 4.初始点是x0=(1,-2)T.

表1中，比较了本文的算法与文献[16]的算法.NF和NG分别表示目标函数f和梯度的计算次数.IT 表示迭代次数.此外，用“-”表示在文献[16]中没有给出的值，f*是最优解.

表1中的结果表明，与文献[16]中算法相比，本文的算法是有效的,3个问题的迭代次数令人满意.

表1 文献[16]中算法与算法A的数值结果比较

4 总结

在该方法中，试探点的接受准则是灵活的，拒绝区域是根据以往试探点的不同表现而变化的，而在传统的滤子方法中，滤子结构中的元素是固定的.数值计算结果表明，与传统方法和Matlab算法相比，新方法具有更好的计算效率和更小的计算量.此外，该方法中自适应参数的使用和调整是平衡目标函数和约束违反度函数值的一种很好的方法.