基于LLCL型并网逆变器的复合控制方法

刘 洋， 杨旭红*， 郭 凯， 吴 斌， 陈 昊， 张云飞

(1.上海电力大学自动化工程学院， 上海 200090； 2.国网滨州供电公司， 滨州 256600； 3.国网温州供电公司， 温州 325000)

并网逆变器是新能源发电设备与电网连接的重要组成部分,其性能对并网电能质量有着重要影响[1-2]。目前中外学者对于电感(L)型、电感-电容(LC)型以及电感-电容-电感(LCL)型并网逆变器做了大量研究，控制方法[3]也已经相当成熟。然而大部分研究仅仅关注并网电流总谐波畸变率(total harmonic distortion，THD)而往往忽略了(pulse width modulation，PWM)调制方式所带来的开关频率处的谐波电流成分[4-5]。

通过在滤波电容支路与小电感串联形成LC串联谐振支路，同时将串联谐振频率设定为开关频率,可以大大降低开关频率处的谐波分量，串联电感量极小因此可以忽略其带来的附加成本[6]。

除上述的LLCL滤波器，五阶以下滤波器的拓扑结构还有6种[7]，但满足低频高阻和高频低阻特性的只有两种，二者均保证了高频衰减能力，但电路设计十分复杂，而且采用串联阻尼电阻法不仅增加有功损耗，还降低了对开关频率处谐波的衰减能力。

将两个LC串联谐振支路并联在滤波电容器两端构成双陷波开关频率滤波器，确保滤除开关频率及其倍频处谐波成分，同时降低了无源阻尼带来的消耗，但其仍对并网能量的传递效率带来影响，并且并联支路的引入会产生多个正向谐振峰值，这不利于控制系统的稳定,相应的控制器设计将变得更加复杂[8]。在LC谐振支路的电感L两侧并联阻尼电阻的基础上，同时在LC支路两侧并联电容，这种方法虽然保证了复合型电感-电感-电容-电感(LLCL)滤波器高频具有-60 dB/十倍频的衰减能力，但其开关频率处的衰减能力也被大大削弱[9]。此外由一个LC串联谐振和一个LC并联谐振组成的混合谐振滤波器，对两个滤波电容的选取十分严格，若选取不当反而会放大谐波，造成严重后果。同时附加的电容也会增加无功损耗和设计成本[10]。

类似于LCL型逆变器，LLCL型逆变器也存在谐振问题，目前LLCL型逆变器谐振抑制方法大多数停留在无源阻尼层面上[11-14]。采用加权平均电流控制[15-16]的方法虽能实现降阶作用但不能保证对并网电流的直接控制，采用电容电流反馈的有源阻尼法简单可行，同时也可以达到抑制谐振尖峰的效果且不会增加系统额外的有功损耗[17]。

综合考虑电路设计及控制方法的复杂程度，选取性能较好的LLCL型并网逆变器作为控制对象，在两相静止αβ坐标系下采用电流双环控制策略：外环使用比例复数积分(proportional complex integral，PCI)控制器和准比例谐振(quasi-proportional resonance，QPR)控制器并联实现对并网电流信号无静差跟踪，内环用串联谐振支路电流反馈的有源阻尼控制消除谐振，同时加入电网电压比例前馈增强系统的抗干扰能力，最后通过仿真实验证明了控制策略的可行性与LLCL型滤波器的优越性。

1 LLCL并网逆变器拓扑结构

三相LLCL并网逆变器主电路如图1所示。图1中，Vdc为直流电压源，S1～S6为电力电子功率开关管，L1为逆变器侧的电感，L2为并网侧电感，串联谐振电感Lf和电容C构成串联谐振支路。i1k、ick和i2k分别表示流过逆变器侧，串联谐振支路以及并网侧的电流，Ugk为三相电网电压(其中k=a、b、c)。

LLCL滤波器的等效控制模型如图2所示。图2中，uinv(s)表示逆变器输出电压的拉氏变换，ug(s)表示电网电压的拉氏变换，i1(s)和i2(s)分别表示逆变器侧电流和并网侧电流的拉氏变换。

根据图2可求得uinv(s)到i2(s)的传递函数G1(s)为

(1)

式(1)中：s表示复频域内的自变量。

当式(1)中的Lf=0时，可得LCL型并网逆变器的传递函数。

由于LLCL型滤波器存在串联谐振支路,因此其应该具有两个谐振频率fres、fsw，其表达式为

(2)

(3)

式中:fres为LLCL滤波器的谐振频率；fsw为串联谐振支路的谐振频率。

图3为LLCL型和LCL型滤波器伯德图，其中fres_LCL为LCL型滤波器的谐振频率，各元器件参数如表1所示。观察幅频特性曲线(图3)可知，在中低频段LLCL型滤波器同LCL型滤波器特性基本相同，均具有谐振峰值。而在高频段LLCL滤波器和LCL滤波器分别以-20 dB/十倍频和-60 dB/十倍频的速率对高次谐波进行衰减,因此在高频段LLCL滤波器作用稍显逊色，但值得一提的是，由于LfC支路的串联谐振作用，使得LLCL滤波器在fsw处具有负向的高增益，可以大幅度衰减开关频率的谐波成分，弥补了其衰减能力不足的缺点。

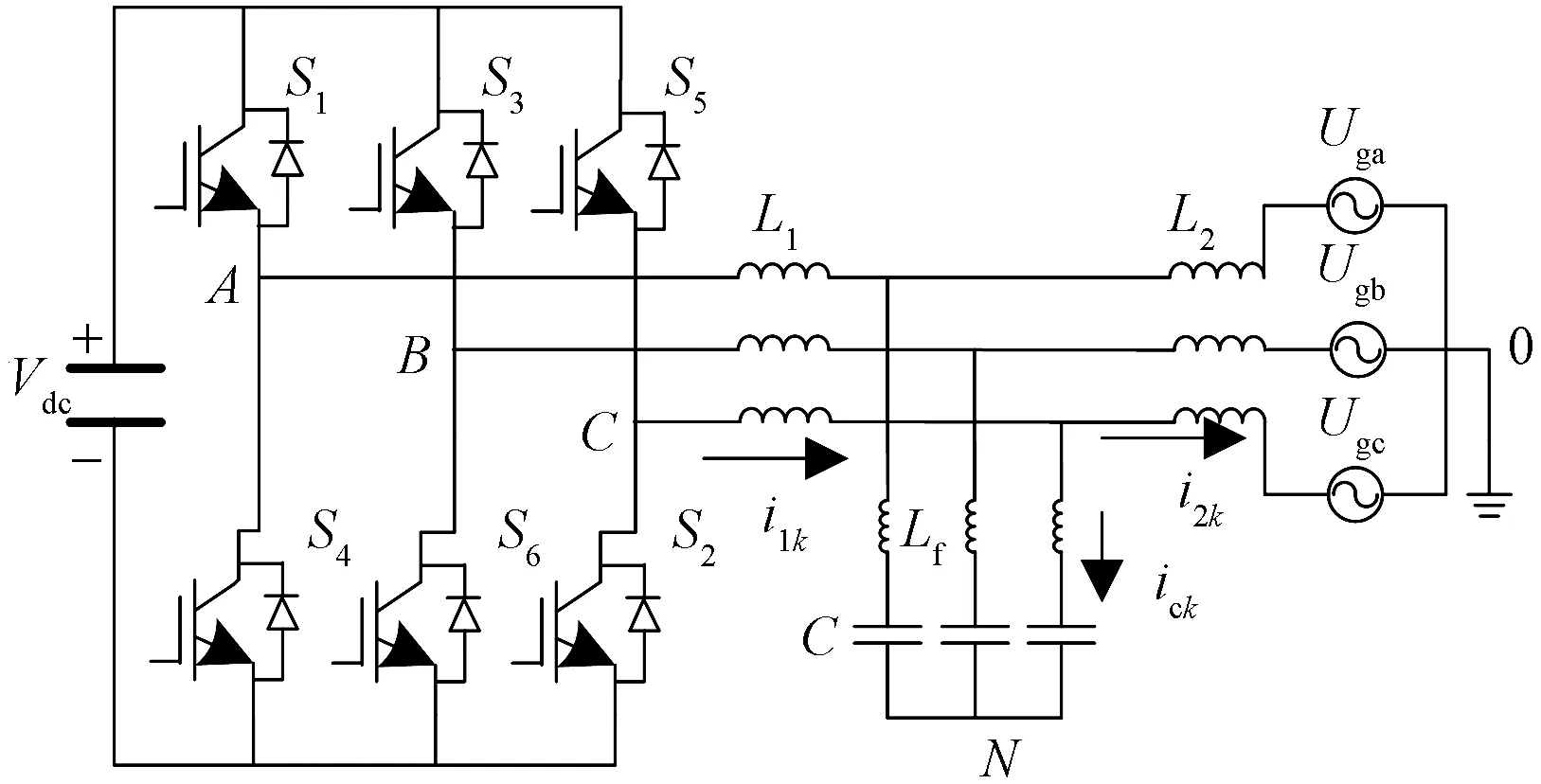
图1 LLCL并网逆变器主电路Fig.1 Main circuit of LLCL grid connected inverter

图2 等效控制模型Fig.2 Equivalent control model

图3 滤波器幅频特性曲线Fig.3 The amplitude-frequency characteristic curve of the filter

2 电流双闭环控制策略

图4为电流双闭环控制策略等效控制框图。忽略电网电压干扰项，根据图4可得控制器输出信号u(s)到并网电流i2(s)的开环传递函数为

iref(s)为并网参考电流的拉式变换；G(s)为控制器的拉氏变换；u(s)为控制器G(s)输出 信号的拉式变换；Kpwm为逆变器等效增益，1/Kpwm为电网电压前馈系数；K为电容电流的反馈系数图4 等效控制框图Fig.4 Equivalent control block diagram

(L1+L2)s}-1

(4)

式(4)中：u(s)为外环控制器输出信号的拉氏变换；Kpwm为逆变器的等效增益；K为电容电流反馈系数。

如图5所示，在加入电容电流反馈支路后，LLCL滤波器的正向谐振峰被消除，同时开关频率处的衰减特性不受影响。

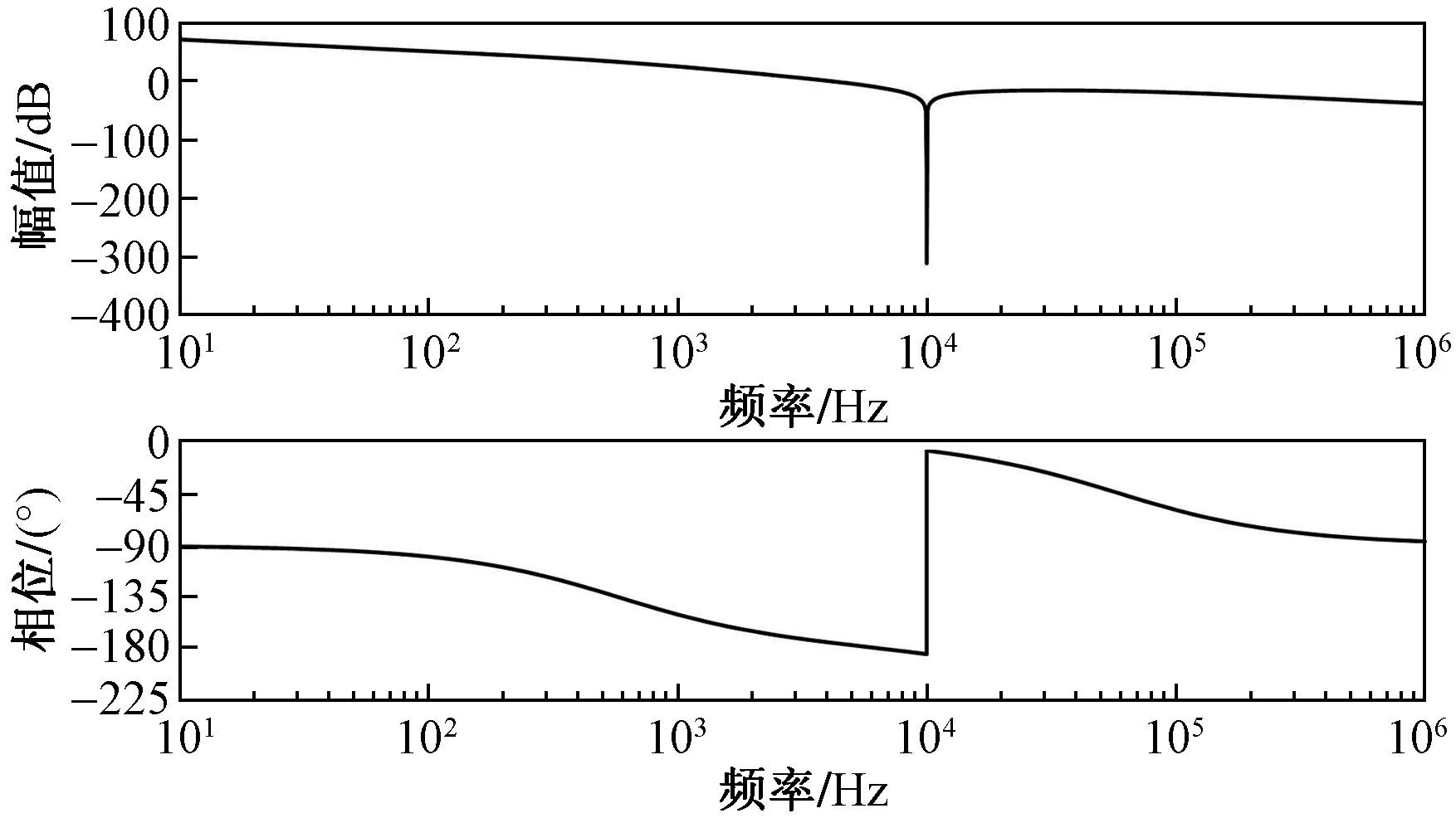
图5 开环传递函数频谱图Fig.5 The amplitude-frequency characteristic curve of the open-loop transfer function

3 外环复合控制器

比例积分(proportional integral，PI)控制器是将阶跃信号作为内模，因此对交流信号的增益是有限的,不能实现交流信号的无静差跟踪,这一点可以从式(5)表示的PI控制器的传递函数上看出。

(5)

式(5)中：KP1为比例系数；KI1为积分系数。

比例谐振(proportional resonance，PR)控制[18]不仅能够实现交流信号的跟踪，还能在特定频率实现高增益，但比例谐振对系统要求较高，式(6)中ω0=314 rad/s，观察式(7)可知，当系统的运行频率发生变化(即ωω0)时，比例谐振控制在工频50 Hz处的控制效果会下降，对频率实时变化的电网的适用性较差，PR控制器的传递函数为

(6)

式(6)中：KP2为比例系数；Kr为谐振系数；ω0为基波角频率且ω0=314 rad/s。

(7)

式(7)表示的准比例谐振(QPR)控制不仅能在基频处实现良好的跟踪性能，同时满足一定的带宽要求，保证电网频率变化时仍然可靠[19-20]。准比例谐振控制器的传递函数为

(8)

式(8)中：kp1为比例系数；kr为谐振系数；ω0为基波角频率；ωc为带宽且ωc=2frad/s，其中f为系统频率偏移量。

式(9)的比例复数积分(PCI)控制器是基于复数域的控制器，其可以实现交流无误差控制。PCI控制器的传递函数为

(9)

式(9)中：kP为比例增益；kI为积分增益；ω0为基波角频率。

其两相静止坐标系下的具体控制器结构如图7所示。

图7中，ex(x=a、b、c、α、β)为并网电流的误差信号，yx(x=a、b、c)为输出信号。由于控制器是基于复数j形式，由前面分析可知αβ坐标系中eα=jeβ，eβ=-jeα，由此可以实现复数j。

PCI和QPR并联的新型复合控制器对应的传递函数为

(10)

3.1 PCI控制器参数设计

并联复合控制器参数设计比较复杂，为了方便分析，通常将两种控制器按照各自控制特点单独进行参数设计。

对于PCI控制器来说，将其单独应用到系统中时，对应的PCI控制下的闭环传递函数为

图6 3种控制器的幅相特性曲线Fig.6 Amplitude-phase characteristic curves of three controllers

abc表示表输入的a、b、c三相的信号图7 比例复数积分控制器的结构Fig.7 The structure of the proportional complex integral controller

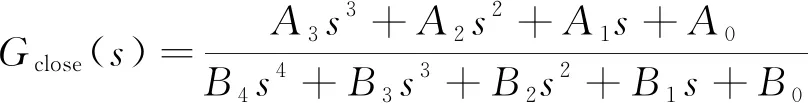
(11)

式(11)中：

(12)

(13)

将s=jω分别代入式(12)、式(13)可得系统闭环传递函数的幅频特性函数|Gclose(jω)|和相频特性函数∠Gclose(jω)：

(14)

(15)

式中：

(16)

当被控量为基频信号即ω=ω0时，代入式(14)、式(15)中，可得PCI控制下系统闭环幅频特性|Gclose(jω0)|=1，相频特性∠Gclose(jω0)=0，故能实现无静差控制。

根据PCI控制器中的参数设计方法可知[21],系统带宽(fb)要控制在500～2 000，即大于10倍的基波频率且小于1/10倍的开关频率。

选取系统带宽fb=650 Hz，即带宽角频率ωb=2πfb=4 082 rad/s。为了方便计算控制器的参数，结合系统带宽的定义式20lg|Gclose(s)|s=jωb=-3并且先定ki为0，即仅考虑kP时将ω=ωb=4 082 rad/s代入式(14)所示的幅频特性表达式中，可初步计算PCI控制器的比例系数为0.4。

PCI控制器中积分系数kI的引入会影响系统的带宽大小，若保证带宽fb在规定的范围之内，设fb=700 Hz，即ωb=4 398 rad/s，代入式(14)中计算可得kI=210。

3.2 QPR控制器参数设计

当控制器为QPR时，系统的闭环传递函数为

Tclose(s)=(M4s4+M3s3+M2s2+M1s+M0)×(N5s5+N4s4+N3s3+N2s2+N1s+N0)-1

(17)

式(17)中：

(18)

(19)

QPR控制器中包含kP1、kr、ωc三个参数，若按照式(17)所示的高阶闭环传递函数去逐个分析并计算具体的控制参数将避免不了复杂的运算过程，所以此次采用比较简便且快速的定二调一的选参方法[22]：在其中两个控制参数不变的前提下，观察第3个参数变化对控制效果的影响，以此类推，分析各个参数变化对系统控制效果带来的影响，然后再反复多次调参确保控制器能达到较好的控制效果。

图8(a)、图8(b)分别表示取kP1为0、kr为1，仅ωc变化时QPR控制器的幅值和相位曲线。观察两图可以发现ωc增大时，带宽也随之增大，而且在除基波角频率ω0=314 rad/s以外的角频率处，控制器的增益也随着ωc增大而增大，但是ω0处的增益保持不变。

图9(a)、图9(b)分别表示取kP1为0、ωc为1，仅kr变化时QPR控制器的幅值和相位曲线。由图9可知，kr的变化仅影响控制器的增益，且kr越大增益越高也即系统的稳态误差越小。

图10(a)、图10(b)分别表示取kr=1、ωc=1，仅kP1变化时QPR控制器的幅值和相位曲线。kP1在一定范围内时，控制器的带宽以及增益均受到kP1的影响，当kP1过大时，控制器总体相当于一个比例增益环节。

为了衡量控制器的抗扰性能，一般将谐波阻抗ZQPR定义为谐波电压(Ut)与谐波电流(It)的比[23]。

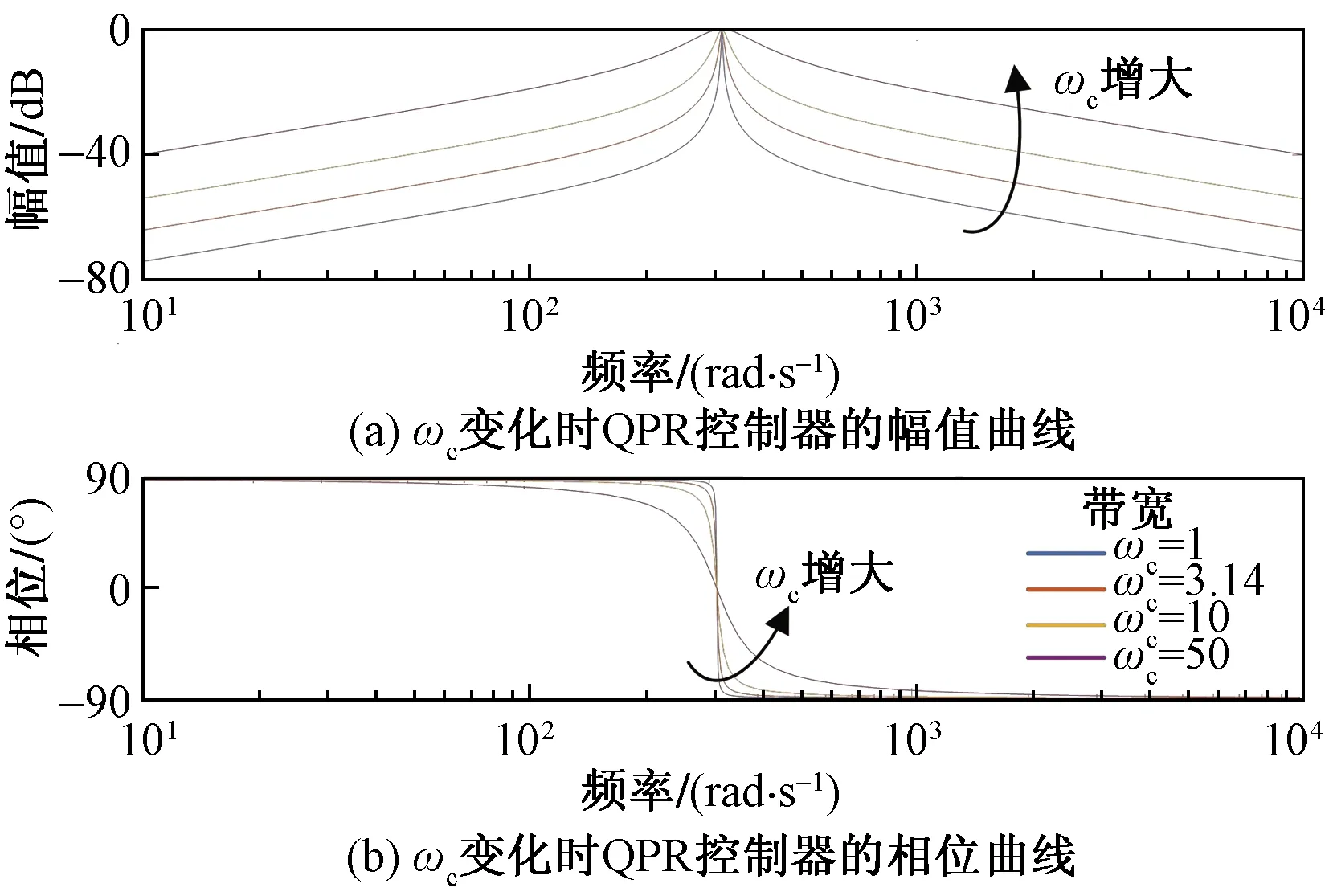
图8 ωc变化时QPR控制器的幅相特性曲线Fig.8 The amplitude and phase characteristic curve of QPR controller when ωc changes

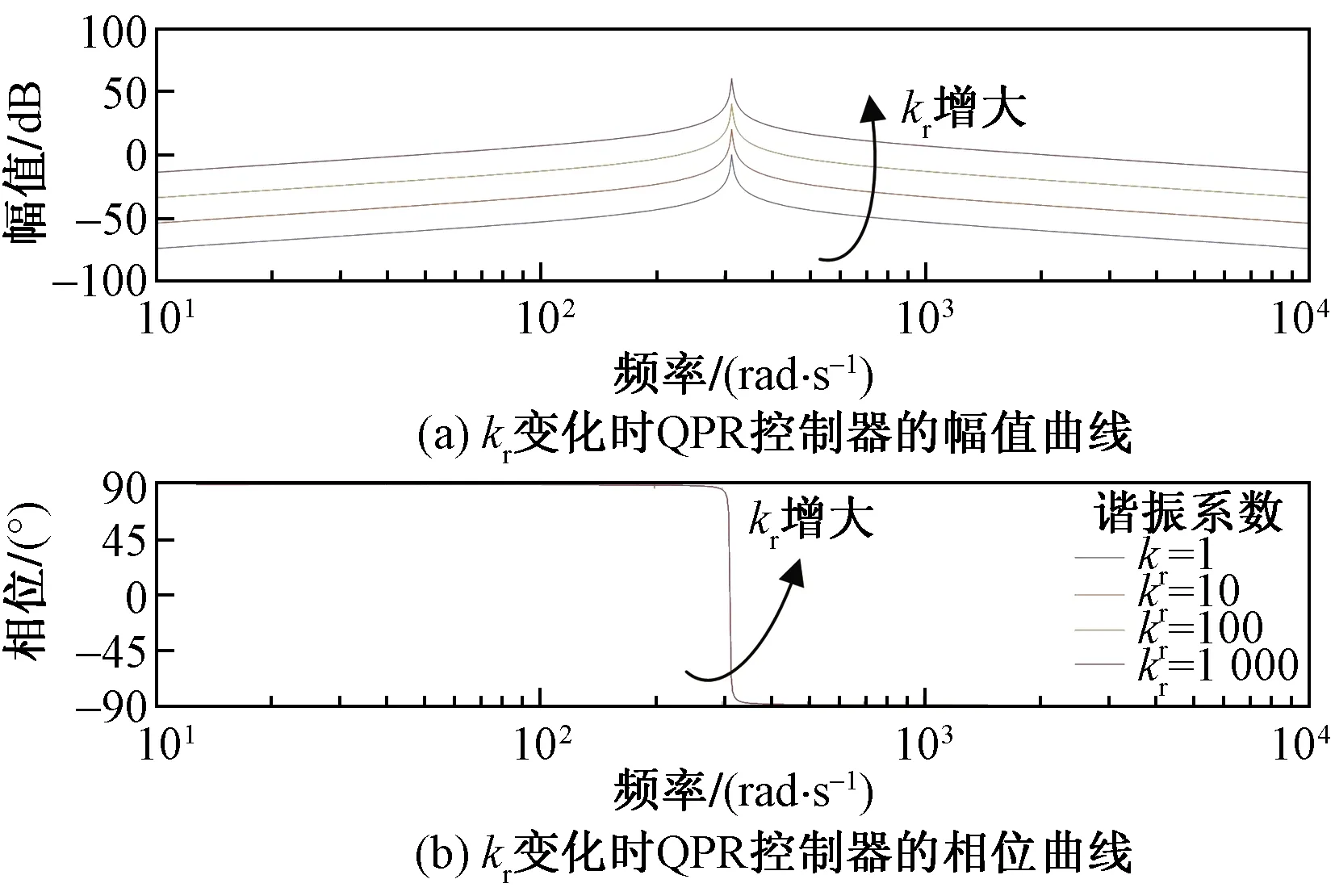
图9 kr变化时QPR控制器的幅相特性曲线Fig.9 The amplitude and phase characteristic curve of QPR controller when kr changes

图10 kP1变化时QPR控制器的幅相特性曲线Fig.10 The amplitude and phase characteristic curve of QPR controller when kP1 changes

如果谐波阻抗越大，那么就意味着谐波电流越小，系统的抗扰性能越好。

LLCL滤波器谐振频率fres之前的频段内，LLCL滤波器和L型滤波器以及LCL滤波器的特性基本一致。为便于分析，将其等效为L型的滤波器，因此系统的谐波阻抗可以表示为

(20)

式(20)中：

(21)

取kr=11、ωc=3.14，图11(a)、图11(b)分别为系统谐波阻抗的幅值曲线和相位曲线。当kP1变化时系统的谐波阻抗会受到影响，且kP1增大，谐波阻抗越大，系统的抗扰性越好。

综上所述，QPR控制器参数的设计步骤为：①根据电网频率所允许的波动区间确定ωc；②根据控制所需选取谐振系数kr；③最后根据谐波阻抗来选取合适的比例系数kP1以使得控制效果最好。

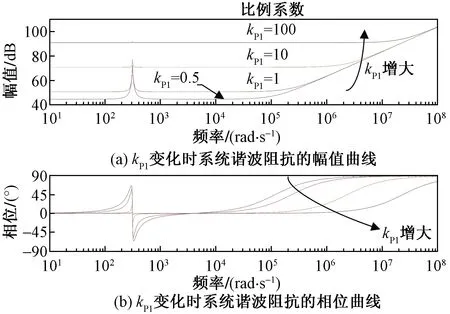
图11 kP1变化时系统谐波阻抗的幅相特性曲线Fig.11 The amplitude-phase characteristic curve of system harmonic impedance when kP1 changes

4 仿真分析

为了验证LLCL型逆变器在复合控制策略下的优越性,在MATLAB/Simulink中分别搭建了LCL型和LLCL型两种逆变器的模型,并进行仿真验证。其中比例复数积分(PCI)控制器参数分别为kP=0.4,kI=210，准比例谐振(QPR)控制器参数为kP1=0.9,kr=11。表1为实验的系统参数和组件参数。

图12分别为LCL、LLCL型逆变器在单一PCI控制下的A相并网电流的谐波失真率,比较两图可以看到LLCL型滤波效果优于LCL滤波器，通过观察二者开关频率附近的高频谐波可以发现，使用LCL型滤波器时并网电流的高频谐波分布在开关频率(fsw=10 kHz)附近，且含量约为0.5%，而使用LLCL型滤波器在开关频率附近的高频谐波由于LfC串联谐振支路在开关频率处的零阻抗作用使得此频率处的高频谐波成分被有效滤除了。

图13为所提复合控制方法下LCL和LLCL型逆变器的A相并网电流的谐波失真率，分别与图12中的两图进行比较可知复合控制方法较单一PCI控制方法而言，能有效降低谐波畸变率，提高并网电流质量。

图14为当0.14 s外部参考电流指令改变时A相电网电压(1/5处理)与并网电流的波形。当电流指令变化时，单一PCI控制下的电压电流虽能保持同相位，但由下方电流局部放大图可知，电流的波形质量明显变差,此时的谐波畸变率为3.96%，即仅使用PCI控制器时不能保证良好的动态性能。

图15为当采用新型复合控制方法后改变参考电流指令时的A相电网电压(1/5处理)和并网电流波形。观察可知指令变化前后电压与电流始终保持同频同相,根据图中电流局部放大可以看到0.14 s后的电流波形正弦度较图14更高，此时谐波畸变率为1.95%远低于3.96%。因此在复合控制器的作用下，能够保证系统拥有良好的动态性能，保证电流质量。

表1 仿真模型基本参数Table 1 Basic parameters of the simulation model

图12 单一PCI控制下的并网电流FFT分析Fig.12 FFT analysis of grid-connected current under single PCI control

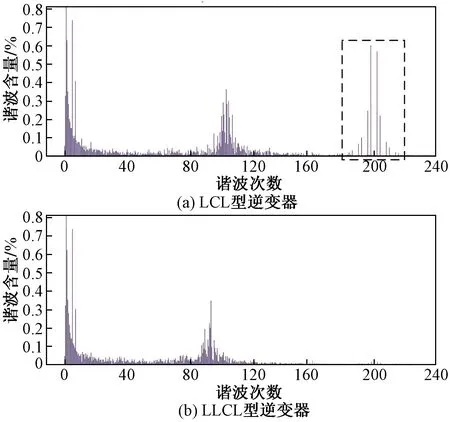
图13 新型复合控制方法下的并网电流FFT分析Fig.13 FFT analysis of grid-connected current under new combinedcontrol method

THD为总谐波畸变率图14 PCI控制Fig.14 PCI control

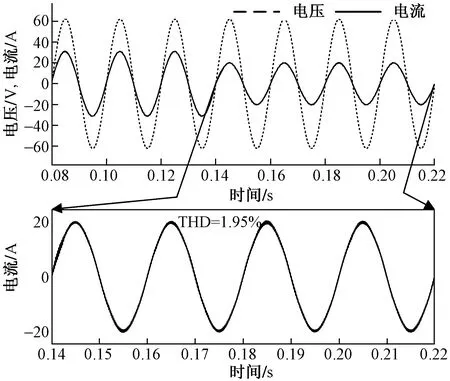
图15 新型复合控制Fig.15 New composite control

5 半实物仿真验证

为了进一步验证所提出的复合控制方法的可行性和有效性，搭建了基于实时仿真平台(RT-LAB)的半实物仿真模型对所提方法进行验证。

实验参数设置与Simuink仿真模型参数设置保持一致。图16为基于PCI和QPR复合控制器作用下的LLCL型并网逆变器入网电流实验波形，三相并网电流能够在极短时间内进入稳定状态且最终保持在参考值附近，由于定步长设置的影响，波形图中难免存在一些毛刺，但电流波形总体质量较好，实验波形与Simulink仿真波形基本一致。

图17为该复合控制策略下的A相电网电压与入网电流实验波形，观察可知，电压电流在很短的时间内便达到同频同相，稳态情况与仿真分析结果大致相同。

图18为外部参考指令发生跳变后三相入网电流的波形情况，当外部有功参考电流降为20 A时，由于PCI和QPR复合控制器的调节作用，使得入网电流能快速跟踪外部参考指令电流，电流到达稳定状态所需的时间极小，且电流质量较高。如图19所示为系统的实物图。

为证明RT-LAB半实物仿真实验结果的可靠性和有效性，周林等[24]用RT-LAB成功验证了光伏系统控制中广泛采用的MPPT(最大功率跟踪)法，并指出RT-LAB仿真平台可为实时性要求高的微电网系统中控制算法的验证提供可靠的依据。

图16 三相并网电流波形Fig.16 Three-phase grid-connected current waveform

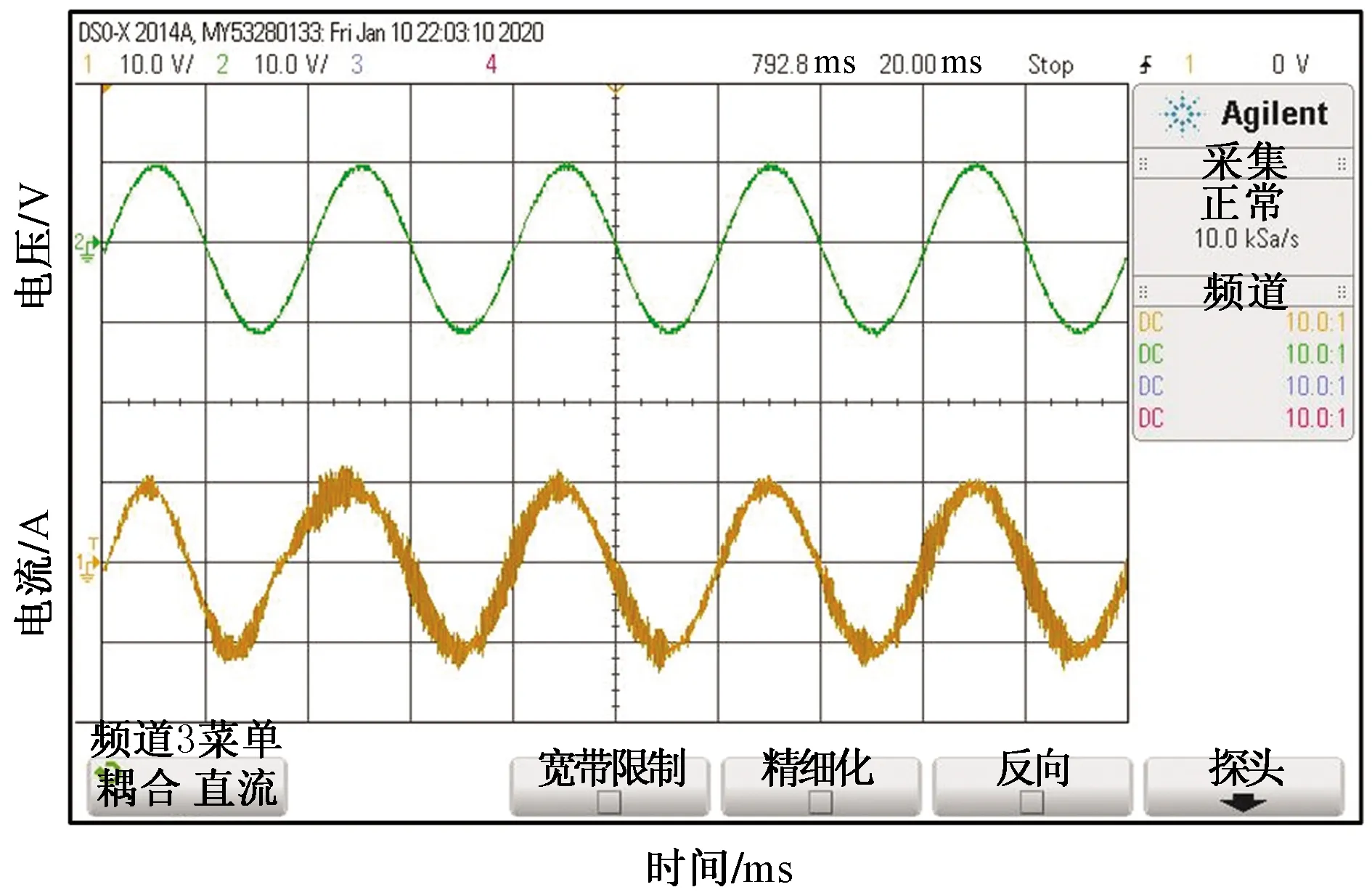
图17 A相电压和电流波形Fig.17 Phase A voltage and current waveform

图18 外部指令跳变时电流波形Fig.18 Current waveform during external command transition

图19 系统实物图Fig.19 System physical map

汪谦等[25]通过RT-LAB实时仿真平台成功地对多电平换流器柔性直流输电系统进行了仿真验证，将所得结果与PSCAD中的离线仿真结果进行效率和准确性方面的对比后发现暂态及稳态结果基本一致，证实了RT-LAB的仿真结果可以为柔性直流输电系统的仿真及应用提供有力依据。

综上所述，RT-LAB半实物仿真平台能够获得与实际工程应用基本一致的实验效果，可以为控制策略最终验证提供重要的参考价值。

6 结论

基于LLCL型并网逆变器提出了PCI与QPR并联复合控制策略。并借助MATLAB/Simulink和RT-LAB半实物仿真实验平台分别搭建了控制模型。通过理论分析与仿真实验可得到以下结论。

(1)由于串联谐振的影响，LLCL型逆变器在开关频率附近具有比LCL型逆变器更强的谐波抑制能力，能更好地提高并网电流质量，并且LfC串联谐振支路的谐振电感Lf极小，其附加成本可以忽略。

(2)采用新型复合控制策略不仅能够提高并网电流的质量，实现单位功率因数并网，还能保证系统在外部参考指令变化时具有较强的动态跟踪能力，更容易满足实际工程需要。