精密机床主轴的有限元分析
2020-12-28郑银环刘王智懿王小康
郑银环,刘王智懿,王小康
(武汉理工大学 机电工程学院,湖北 武汉 430070)
研究表明机床主轴回转误差引起的精密加工误差约为30%~70%,且所占比例与机床精度成正比[1]。早在1988年,Sdaeghipor在研究主轴系统动态特性时,创造性地引入了动柔度这一参数,得到了较为准确的分析结果[2]。1991年,Spur等对机床主轴的轴承结构进行了适当修正,获得了较为精确的静力学和动力学特性[3]。1994年,肖曙红基于数学迭代并结合有限元法,开发了主轴系统静力学和动力学性能分析程序[4]。1997年,Bert等构建了主轴的动态模型,研究了主轴的动力学性能和热特性[5]。2003年,Lin等建立了较为精确的电主轴动力学模型,得出了主轴刚度与轴承预紧力有很大的关联[6]。同年,Xiong等结合有限元法,分析了转子陀螺效应对电主轴系统动力学性能的影响[7]。2007年,林士龙等利用有限元分析方法在设计过程中就得到了主轴的动态特性,得到了较为准确的分析结果[8]。2008年,Yang等建立了某新型铣床的有限元模型,着重分析了其动力学性能[9]。2009年,钱学毅采用有限元法研究车床主轴系统的动力学性能,确定了主轴系统的前8阶固有频率、振型及最大综合变形,分析了不同的结构参数对主轴系统动态性能的影响[10]。2013年,刘丹萍等使用ANSYS软件建立了数控机床主轴的有限元模型,分析了机床主轴的模态特性,研究了主轴动力学参数对加工精度的影响,分析结果为提升主轴性能和效率发挥了重大作用[11]。2015年,谭峰对微型数控车床的主轴进行了有限元仿真分析,结果表明设计的主轴的强度和刚度均能满足使用要求[12]。
综上所述,有限元法常用来计算主轴系统的特性,并取得了一些成果。但已有文献大多研究的是机床主轴的某一方面的特性,针对纵切机床主轴系统这种特殊结构研究较少,笔者以某精密多轴机床的主轴为研究对象,使用有限元法对其静态、动态性能进行研究,检验其设计合理性。
1 有限元模型的建立
以某精密多轴机床的主轴系统为研究对象,建立主轴系统的三维模型如图1所示。
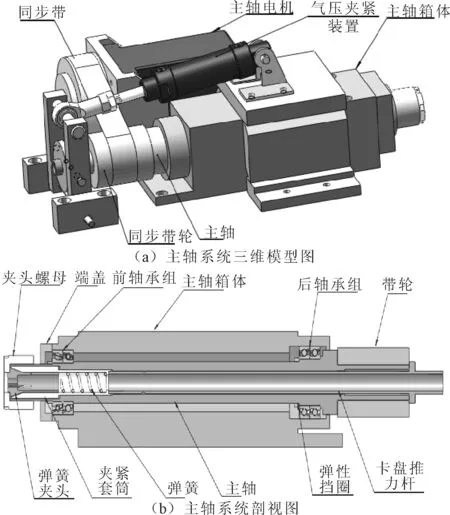
图1 某精密机床主轴系统结构图
建立主轴的有限元模型时,对结构进行了如下简化:
(1)将前后两组角接触球轴承简化为弹性支承,用弹性约束模拟;
(2)假设经过预紧后的角接触球轴承只有径向刚度,且为定值,忽略其角刚度,并将弹性支承等效为一组弹簧-阻尼单元,并且在自由振动状态下,将阻尼值设置为零;
(3)由于轴承预紧力的作用,不计外界载荷和转速对于径向刚度的影响;
(4)去掉一些不影响最终结果的细小特征,如圆角、倒角和键槽等。
主轴材料选用40Cr,调质处理,其杨氏模量为211 GPa,泊松比为0.211,密度为7 870 kg/m3,屈服强度为785 MPa。选择网格类型为hex dominant,将网格尺寸定为4 mm。模型有9 918个单元,38 924个节点。
根据实际情况施加边界条件,约束前轴承组轴向和切向方向,约束后轴承组切向方向。根据轴承选型和相关公式[13-14]推导,可知前、后端圆柱面的径向刚度分别为154.82 N/μm和169.92 N/μm。主轴在实际运行过程中,工件切削产生的作用力主要由主轴前端的导套承受,故只需考虑主轴的所受力矩,其主要为主轴电机通过同步带传递力矩,计算可得主轴所受的力矩为23.1 N/m。
2 主轴静态性能分析
静态性能分析的目的是为了校验主轴的强度和刚度是否符合设计要求,因而只需要分析主轴静态变形和等效应力的变化情况。主轴的变形和等效应力分布情况如图2所示。

图2 主轴静态分析结果
主轴后端在转矩的作用下变形量较大,最大变形量为0.005 553 1 mm,根据主轴所受的力矩23.1 N/m可求出主轴后端所受切向力为871.7 N,径向力为371.3 N。根据径向力和最大变形量可计算主轴的静刚度为567 000 N/m,故主轴刚度满足设计要求。
主轴后端所受应力最大,最大值为23.836 MPa。由于主轴材料为40Cr,取安全系数为1.4,屈服极限为785 MPa,许用应力为560.7 MPa,而主轴最大应力为23.836 MPa,远小于许用应力,故主轴强度满足设计要求。
3 主轴动态性能分析
3.1 模态分析
对主轴进行模态分析,进行求解计算后得到主轴前六阶模态的固有频率和振型,如图3所示。主轴各阶固有频率和振型如表1所示。

图3 主轴模态分析结果

表1 主轴前六阶固有频率和振型
由图3和表1可知,主轴的一阶和二阶固有频率近似相等,振型相互正交,因而认为它们是重根;同理,三阶和四阶固有频率也基本相等,因而认为它们也是重根。由于主轴具有多阶固有频率,因而主轴也具有多个临界转速,在工程实际中,通常确保主轴的最高工作转速小于一阶临界转速,一般小于一阶临界转速的75%[15],由一阶固有频率可得一阶临界转速为172 950 r/min,由电机选型可知主轴的最高工作转速为10 000 r/min,远小于其一阶临界转速的75%,因而主轴在整个工作转速范围内是安全的,不会发生共振。
3.2 谐响应分析
谐响应分析是指在外界激励作用下,系统各部分的位移响应。对主轴后端施加切向力871.7 N和径向力371.3 N,由模态分析结果可知,在一、二阶固有频率时,主轴中部和尾端的变形量较大,选择主轴中部为观测对象,可设定频率范围为1 500~3 000 Hz;而在三阶、四阶固有频率时,主轴尾端的变形量最大,设定频率范围为3 500~4 000 Hz。谐响应分析结果如图4所示。
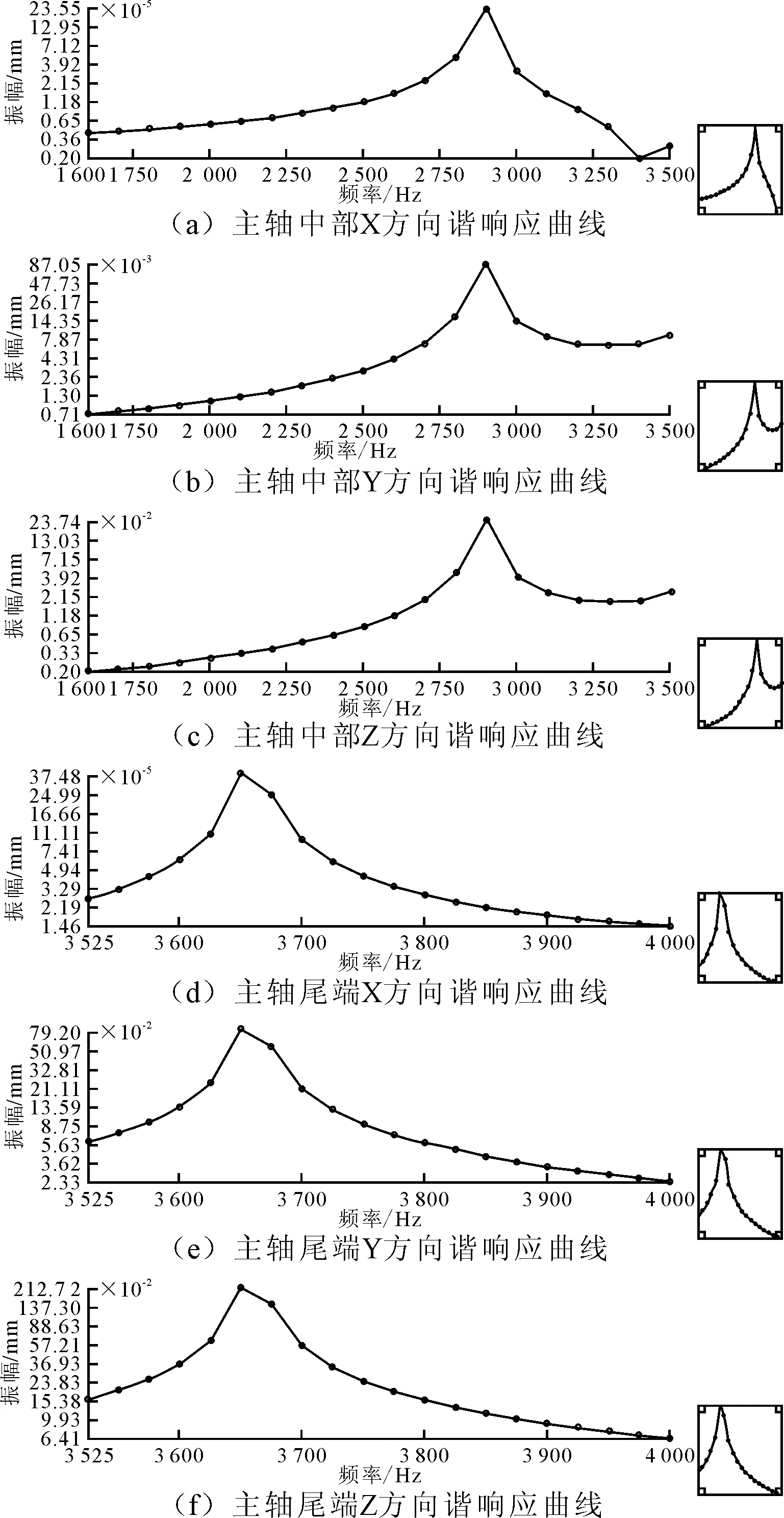
图4 主轴谐响应分析结果
由图4可知,当激振频率为2 800 Hz时,主轴中部的位移急剧增加,并且X、Y、Z 3个方向上Z方向的位移量最大,达到0.237 42 mm。当激振频率为3 600 Hz时,主轴尾端的位移显著增大,在X、Y、Z 3个方向上Z方向的位移量最大,达到2.127 2 mm。而主轴的最高转速对应的激振频率为166.7 Hz,远小于谐响应频率,因此主轴在其工作区间内可以有效避开共振区域。
4 结论
根据设计的主轴系统建立其有限元模型,分析其静态和动态性能。在静态性能分析中,得到了主轴的最大变形量、最大等效应力,结果表明主轴的强度和刚度均符合设计要求。在动态性能分析中,对主轴进行模态分析,得到了主轴的前六阶固有频率和振型,通过谐响应分析得到主轴在低阶频率范围内的位移曲线,结果表明,主轴的工作频率与其固有频率相差较远,在工作转速范围内不会发生共振。
