单Kinect+圆盒的多视角三维点云配准方法研究

黄思捷，梁正友，2，孙宇，李轩昂

（1.广西大学计算机与电子信息学院，南宁530004；2.广西多媒体通信与网络技术重点实验室，南宁530004）

0 引言

利用三维扫描技术对物体进行三维重建是当今游戏、影视、虚拟现实、增强现实中的一项新技术，已被广泛应用到游戏、影视动漫、虚拟现实、产品展示、人机交互、机器人导航控制等诸多领域。在应用方面，刘振[1]利用Kinect 对地面进行土壤表面的三维点云形态结构模型构造通过彩色图像、深度图像和点云初始配准的方法。郑立华[2]用Kinect 相机获取不同视角下果树的原始三维点云，针对传统最近点迭代算法对待配准点云的空间位置要求苛刻的问题，提出了改进的点云配准算法，完成对苹果书的建模。吴剑锋[3]针对Kinect Fusion 硬件要求高，重建效率低，无法满足快速地重建场景的缺点。提出基于点云融合算法的Kinect 快速三维重建算法，应用Kinect 的多深度图像融合的三维重建算法实现目标物体的三维重建。

为重建出完整的三维模型，需要对建模物体从不同的视角进行扫描，每次扫描的获得的点云（待配准点云）往往拥有独立的局部坐标系统，需要转换成统一的全局坐标，这一过程称为点云配准[4]。点云配准是三维重建的核心步骤，配准精度会直接影响三维模型的整体精度[5]。

根据采集视角数的不同，点云配准可以分为双视角配准和多视角配准。双视角配准是在输入点云和目标点云之间构造一个三维空间变换，使输入点云在此变换作用下能够最大限度地和目标点云整合成一个整体。其代表性的算法为迭代最近点（Iterative Closest Point，ICP）配准算法[6]，其核心思想是以迭代最近点的方法，使两个点云相互靠近，最终使两个点云之间的距离误差最小。ICP 算法存在的问题是容易陷入局部最优和缺少重叠区域导致配准精度不高。Kristijan Lenac等人[7]把遗传算法和ICP 算法相结合起来，利用遗传算法找到近似匹配点之后，使用ICP 算法来提高精度，收到较好效果。Zhang Hong 等人[8]提出一种半概率裁剪的ICP 改进算法，利用帧对模型方法和帧对帧方法之间转换后，使用传统ICP 算法对相机的姿态进行细化，最后使用TUM RGB-D 数据集来评估配准的精度。

在多视角点云配准下，多视角点云配准是通过计算各输入点云和目标点云之间的刚体变换关系，然后利用变换关系让各输入点云向目标点云进行变换。其代表性的算法是Chen Yang 等人[9]提出的多个视角的顺序配准算法。该算法先随机选择一个点云作为目标点云，然后按照点云之间的对应关系依次以此点云为基准，后一个点云为待配准点云，采用双目视角的配准方法进行配准，依次完成多视角的点云配准。此算法操作方便、易上手，但是前、后点云配准之后会有误差积累，在进行多次进行双目视角的配准之后累计的误差会被放大，最后影响三维模型整体的精度和可靠性[10-11]。针对这些问题，不少学者提出了解决方案。闫利等人[10]提出一种闭合条件约束的配准方法。该方法先采用“点-切平面”迭代最近点算法分别求解各点云之间的坐标转换参数，再以单站点云为配准单元，以转换参数作为I 观测值构建条件方程，以条件平差方法对转换参数作改正以达到全局最优。李健等人[11]提出结合转台约束下利用图像几何特征进行粗配准和使用迭代最近点ICP 算法实现点云的精确配准的方法，对累积误差导致的闭环问题以及不同角度拍摄引起的色差问题，通过全局误差修正与色差修正算法处理，提升重建结果的精度。徐思雨等人[12]设计一个目标函数，将多视角配准问题分解成多个双视角配准问题，提出逐步求精的解决策略获得精确的多视角配准结果。郭瑞科等人[13]提出一种基于KD-Tree（K-维树）点云均匀采样简化算法，通过对传统四点算法（4-Points Congruent Sets Algorithm，4PCS）中的阈值参数进行统一，确定了各误差阈值参数和点云密度之间的关系；然后通过基于姿态校正的方法解决对称视角点云引起的误配准问题。

尽管多视角点云配准研究取得不错的进展，但仍有进一步提高配准精度的需要。本文使用一台Kinect V2 传感器作为采集设备搭建了一套闭合多视角三维点云的配准系统。首先，将建模物体放在旋转圆盒上，利用Kinect V2 对建模物体每隔60°进行一次点云采集，一共采集6 个点云，形成一个有序而且闭环的点云序列。其次，对建模物体0°到180°视角范围内的3 个点云，通过两边的两个点云分别与中间点云使用ICP算法进行两两配准生成前部点云。以同样的方法对180°到360°视角范围内的3 个点云进行处理后生成后部点云。再次，用基于圆盒特征和小型包围盒约束的方法对前部点云和后部点云进行粗匹配。最后，使用基于圆盒特征和SVD（Singular Value Decomposition）奇异值刚性变换矩阵评估法对前部点云和后部进行细匹配。在进行多视角点云配准时，通过精心安排配准的顺序，避免误差累积的问题。同时，提出的粗配准方法和细配准方法都充分利用圆盒的几何特征，通过圆盒稳定和明显几何特征进行基于特征的点云配准，克服传统ICP 需要对前部点云进行迭代计算的缺点。实验结果表明，所提出的方法克服了多视角点云配准的误差累积问题，提高了三维点云的配准质量。

1 系统组成和方法框架

本文基于Kinect V2 的闭合多视角三维测量系统如图1 所示。将待测物体置于圆盒上，Kinect V2 置于物体前方，测量时手动旋转圆盒，Kinect V2 每间隔60°采集一帧图像，待物体旋转一周后采集结束。测量时，把圆盒和待测物体作为建模物体一起扫描。圆盒是一个几何特征明显并且外形变化有规律的物体，其外形在本研究中被当做一个在建模物体中人为加入的作为配准所需要的几何特征。

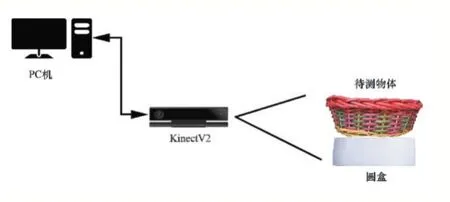
图1 测量系统

为实现对被测目标的闭合多视角三维测量，建立如图2 所示的方法框架，下面对各个主要步骤做一简要说明：

步骤一：采集及预处理。将待测物体放置在一个圆盒上，对圆盒和待测物体每隔60°采集点云一次，获得6 个点云，它们形成一个有序而且闭环的点云序列。然后去除建模物体（含圆盒和待测物体）以外的点云，为随后配准做准备。

步骤二：生成前部点云和后部点云。对建模物体0°到180°视角范围内的3 个点云，用两边的两个点云分别与中间点云用ICP 算法进行两两配准生成前部点云。以同样的方法对180°到360°角范围内的3 个点云进行处理后生成后部点云。

步骤三：粗配准。对前部点云和后部点云的圆盒点云重叠部分分别提取重叠的特征区域，用本文提出的小型包围盒约束粗配准方法前部点云和后部点云进行粗配准。

步骤四：细配准。完成粗配准之后，对前部点云和后部点云的圆盒点云重叠部分分别提取重叠的特征区域，得到重叠特征区域分别记为然后使用基于SVD 奇异值刚性变换矩阵评估法求出的刚性变化矩阵，刚性变化矩阵包括旋转矩阵R和平移矩阵T。并利用求出的旋转矩阵R和平移矩阵T对后部点云进行刚性变换，使它向前部点云进行变换，完成配准。

2 方法详细描述

2.1 数据采集

对建模物体进行点云配准需要采集完整的点云。由于Kinect V2 一次只能采集建模物体一部分的点云；因此，本文采用六面采集方法，对建模物体按圆周顺序每隔60°的不同角度采集六个点云，这些点云包含建模对象的完整点云信息。

Kinect V2 的深度摄像头一般采集范围为z轴方向0.5 米到 4.5 米，y轴方向±60°，x轴方向±70°（根据需求，可适当扩大其采集范围，一定条件下，距离越近精度越高）。由于Kinect V2 采集范围非常大，所以采集到的点云将会包括地面、背景、场景内其他物体等不需要的点云。这些不必要的点云会影响点云配准、特征提取等操作，最后对三维建模的精度造成不良影响。为避免采集到多余的点云，本文对Kinect V2 的采集范围进行精确的设置：z轴范围设定在0.05 米到2 米，x轴范围设定在-0.5 米到0.5 米。同时，还需要对地面点云进行单独采集，以便去除其中包含的地面点云。对建模物体点云进行采集步骤如下：

步骤一：设置Kinect V2 采集的有效范围。将Kinect V2 放置在一个物体上，如图6 所示，使Kinect V2达到一定的高度，因为所采集的物体随后要放在一个圆盒之上。如果Kinect V2 的高度不够，会导致目标物体部分区域无法采集到，导致生成的点云产生残缺和空洞，最终影响随后点云配准精度。

步骤二：对地面进行点云采集，获取地面点云G。

步骤三：将圆盒放置于地面上并进行点云采集，采集圆盒点云C。

步骤四：将目标物体放置在圆盒之上，对目标物体按图3 所示方向以0→1→2→3→4→5 顺序采集点云，获得建模物体的6 个闭合多视角点云序列Mi,i∈{1,2,3,4,5,6}。建模对象点云采集完成。

图3 点云的采集

2.2 点云的预处理

由于采集到的建模物体多视角点云含有地面点云信息以及离群点，需要去除这些干扰配准的点。

对地面点云G遍历其中每一个点并求出在y轴坐标（高度）中最大的值，设为yG_max。然后，对建模物体多视角点云中每一个点进行遍历，若点(x,y,z)的y坐标值小于yG_max，则该点为地面点云，将该点从建模物体多视角点云中去除。

在除去地面点云之后，对建模物体多视角点云还要去除离群点。本文采用PCL（Point Cloud Library）点云库中RadiusOutlierRemoval 滤波器[14]对点云进行采样滤波，其原理是：首先，设置滤波器的两个参数，一个参数为圆的半径长度r，另外一个参数为以r为半径生成圆内包含点云的个数n。然后，在建模物体多视角点云中任取一点云为圆心、半径为r的圆，如果在领域内的点云数量大于n，那么认定该点是非离群点；否则判断该点为离群点，并将其去除。例如，在图3，设半径为r，n为1 时，如图4 中的点云A 将判定为离群点将其去除，而B 和C 的点云将判断为非离群点将其保留。

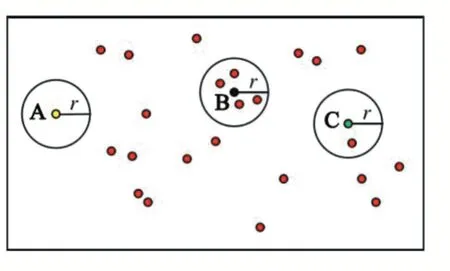
图4 除去离群点

2.3 生成前部点云和后部点云

作为多视角点云配准代表性，顺序配准算法[9]直接易行，但前后配准点云之间有误差累积，影响整体配准的精度与可靠性[10-11]。在顺序配准算法基础上，文献[10-11]采用各种全局优化措施减少误差累计问题，但是计算复杂。本文提出一种解决累积误差的方案，对于采集到的6 个有序闭合视角点云序列，我们对0°至180°的三个点云中的两个两边点云分别与中间点云用ICP 算法进行两两配准生成前部点云。以同样的方法对180°到360°视角范围内的3 个点云进行处理后生成后部点云（本小节）。由于采用两个两边点云分别与中间点云用ICP 算法进行两两配准，而不是对三个点云顺序配准，因此没有产生累积误差。最后，对生成的前部点云和后部点云进行配准（2.4 小节），最终完成闭环多视角点云的配准。

当两个点云有一定的重叠（重叠率超60%情况下），ICP 算法能得到正确的配准结果[15]。按照2.1 小节方案采集点云时，两个相邻的点云有非常大的重叠，可用直接用ICP 算法进行配准。

将采集到的0°至180°的三个点云预处理后记为Ml（左边）、Mm（中间）、Mr（右边）。从上下文可知Ml和Mm两个点云之间在视角上有theta=60°的角度差，Mr和Mm两个点云之间在视角上有theta=-60°的角度差。对Ml（作为输入点云）和Mm（作为目标点云）进行配准，首先使用公式（1）进行旋转操作对输入点云进行变换，随后再使用ICP 进行配准。

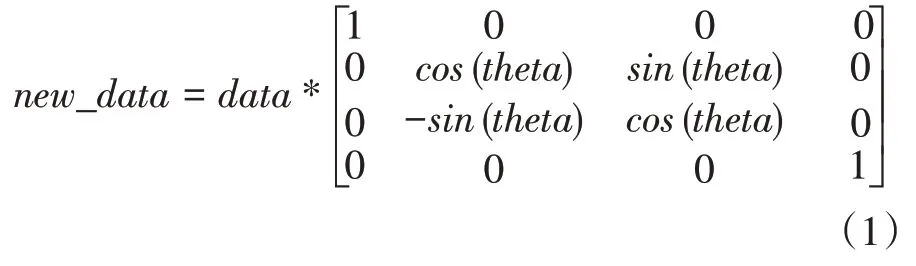
其中data为输入点云，new_data为变换后的点云，theta为输入点云到目标点云的视角差。

对Mr（作为输入点云）和Mm（作为目标点云）Ml(作为输入点云)和Mm(作为目标点云)进行配准，使用公式（1）进行旋转操作对输入点云进行变换，随后再使用ICP 算法进行配准。

通过以上操作，将0°至180°的三个点云配准成前部点云S。用同样的方法将180°至360°视角范围内的3 个点云进行处理后生成后部点云P。生成的前部点云和后部点云为完成建模物体的闭环多视角点云配准打下基础。

2.4 点云前部点云和后部点云的配准

前部点云和后部点云视角差为180°，如图5 所示。两个点云之间重叠区域非常稀少，直接使用ICP算法会由于缺少重叠区域中的特征，造成配准效果差，甚至配准失败。针对以上问题，我们利用建模物体中圆盒具有几何特征稳定的特点，提出利用圆盒特征和小型包围盒约束相结合的粗配准算法，基于圆盒交接区域特征和SVD 奇异值刚性变换矩阵评估法相结合的细配准算法。先用提出的粗匹配算法进行配准，获得良好的初始位置；然后，再用提出的细配准算法进行配准，有效解决上述问题。

2.4.1 基于局部角度阈值的特征提取

前部点云S和后部点云P位置关系如图5 所示（从y轴截面上看）。其中，两圆弧分别代表圆盒前部和后部，4 个圆圈分别是前部点云S、后部点云P在后续配置中要用到的特征区域。我们采用基于角度阈值的特征提取方法提取前部点云S和后部点云P分别对应的特征区域，该方法形式化描述如下：设点云B∈{S,P} ，vector(1 , 0,0 )是x轴正方向向量 (vector正)，vector(- 1,0,0 )是x轴负方向向量(vector负)，圆盒点云C在y轴的最大值与最小值分别为ymax和ymin，用公式（2）对点云B进行特征区域的提取，得到特征区域记为Bt。公式（2）中γ为预设的角度阈值。

图5 前部点云S和后部点云P

2.4.2 使用圆盒特征和小型包围盒约束的粗配准

基于特征的粗配准方法首先要确定要靠拢的特征区域。由于每次建模物体不一样，导致每一个建模物体交接区中的域特征区域的几何特征有很大区别，鲁棒性不高。这种拥有几何特征不明显会的特征区域会导致点云配准精度不高。针对上述问题，本文把建模物体放置在圆盒之上，将前部点云的圆盒部分和后部点云的圆盒部分的特征区域进行点云配准，求解它们的出刚性变换矩阵，随后通过刚性变换矩阵对建模对象和圆盒作为一个整体进行变换。由于使用圆盒，从不同位置分割都不会破坏其几何特征，具有很高的鲁棒性。

设点云S为目标点云，点云P为输入点云，粗匹配的目标是将输入点云P通过平移变换移动到与S交接的位置上。粗匹配的过程如下：

步骤一：对点云S用公式（2）提取到特征区域St，计算出St在x轴的最大值Smax_x和z轴的最大值Smax_z，设定一个包围盒大小的阈值h，如图5 所示。并设包围盒的 4 个顶点分别为：(Smax_x+h,Smax_z+h)、(Smax_x+h,Smax_z-h)、(Smax_x-h,Smax_z+h)、(Smax_x-h,Smax_z-h)。

步骤二：对点云P用公式（2）提取到特征区域Pt，然后计算出其在x轴最大值Pmax_x和在z轴最小值Pmin_z。

步骤三：设阈值Δx为在x轴上P每次移动的量，Δz为在z轴上P每次移动的量。Pmax_x当前所处于位置的x轴坐标值大于(Smax_x+h)，Δx应设负值，Pmax_x当前所处于位置的x轴坐标值小于(Smax_x-h)，Δx应设正值。Pmin_z和Δz也做同样的处理。如果Δx和Δz设置过大，可能会导致每次平移中让Pmax_x和Pmin_z都无法有效进入包围盒范围内。如果Δx和Δz设置过小，会增加迭代的次数。所以设置Δx和Δz合适大小的数值，不仅能让Pmax_x和Pmin_z有效进入包围盒范围内完成粗配准，而且还能减少迭代的次数。对P中的每个点(x,z)进行平移操作使用公式（3）：

步骤四：用公式（3）对点(Pmax_x,Pmin_z)进行平移得到的点用公式（4）判断是否落在包围盒内：

（3）使用圆盒交接区域特征的细配准

在完成前部点云和后部点云粗配准后，前部点云和后云部点集获得良好初始位置，已经具备进行细配准的条件。接下来要对前部点云和后部点云进行基于特征的细配准。

本文所采用细配准方法是把包含建模对象和圆盒的点云作为一个整体来进行刚性变换。首先，设粗配准后的前部点云为S，后部点云为P。使用公式（2）进行分别对S和P特征提取，分别得到相应的特征区域St和Pt。使用SVD 奇异值刚性变换矩阵评估法对St和Pt求出旋转矩阵R和平移矩阵T。最后对后部点云P使用刚性变换公式（公式（5））进行刚性变换。

其中R为旋转矩阵，T为平移矩阵，Pl是刚性变换后的点云。

由于本文是利用特征区域St和Pt进行SVD 奇异值刚性变换矩阵评估法来获取旋转矩阵R和平移矩阵T。而传统ICP 算法中必须对建模物体特征区域的每一个点进行遍历计算，而本文只需要对圆盒的特征区域进行计算，需要计算的点数量比传统ICP 要少，因此，本文的细配准算法计算效率比传统的ICP 算法要高。同时由于引进拥有几何特征明显的圆盒作为特征，避免传统ICP 算法在少量特征点云的情况下配准精度不高的问题，解决了建模物体的前部点云和后面点云配准精度低的问题。

3 实验及结果分析

3.1 实验环境

本文使用Kinect V2 作为深度数据采集的设备。Kinect V2 的深度摄像头适用于室内弱光的环境下，所以本文选择在白天关闭照明的室内进行深度信息采集。在程序实现，本文采用Visual Studio 2015 作为编译环境，并且使用PCL 点云库和OpenCV 作为第三方编程库。所有程序代码在PCL 点云库基础上进行算法改进，采用C++实现，运行于Windows 10 64 位系统、Intel Core i7-7700HQ CPU@2.80GHz 处理器、8G 内存的笔记本电脑上。图6 为本文Kinect V2 拍摄场景和采集目标水果篮子、打印机。

图6 Kinect拍摄场景和采集对象水果篮子、打印机

图6 中，圆盒高3 厘米、直径10 厘米。KinectV2放置在高6 厘米上的矩形石块上，圆盒距离KinectV2 23 厘米。水果篮子高5 厘米、长轴15 厘米、短轴11 厘米。打印机长17 厘米、宽7 厘米、高5 厘米。

3.2 实验和效果分析

3.2.1 实验处理过程

分别用2.2 小节方法对6 个闭合多视角点云序列去背景、除离群点；用2.3 小节方法对分别对0°-180°的三个点云配准生成前部点云（图7 左图），用2.3 小节方法对分别对180°-360°的三个点云配准生成后部点云（图7 右图）；用2.4 小节方法对前部点云和后部点云进行前后配准，得到配准后的点云，如图8 第三列。

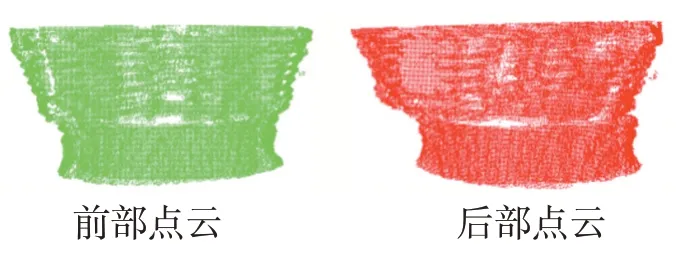
图7 配准获得点云

3.2.2 实验效果分析

我们将本文提出的方法与用顺序配准算法[6]、传统ICP 算法进行对比，实验效果如图8 所示。

图8 水果篮子配准效果图

图8 第一列是文献[6]顺序配准获得的效果图。用2.1 小节采集到的点云，以 1→0→2→4→3→5 按圆周顺序两两用ICP 算法进行配准得到的效果图。在顺序配准的正面视图（图8 第一列第一张图）和反面视图（图8 第一列第三张图）中可以看出，前部点云和后部点云出现严重的穿模，但是点云0、点云1、点云2 利用顺序配准得到配准精度不错的前部点云，后部点云也是亦然。但是顺序配准的问题在于点云2 和点云4 配准的时候，由于这两个点云缺少足够的特征导致配准的精度低下，从左视图（图8 第一列第二张图）和右视图（图8 第一列第四张图）更容易看出前部点云和后部点云严重穿模的程度。并且在随后点云4 与点云3 配准的时候，由于点云4 已经在处于误差非常大的位置上，导致点云3 在点云4 基础上继续配准导致配准的误差被放大。

在前部点云和后部点云形成之后（2.3 小节），需要对前部点云和后部点云进行配准，本文将使用ICP 算法与本文提出的方法（2.4 小节）进行对比，实验效果如图8（第二列、第三列）所示。

图8（第三列）中的第一张图、第二张图、第三张图、第四张图是使用本文方法进行前部点云和后部点云配准的效果图（对应 0°、90°、180°、270°视角），明显可以看到前部点云和后部点云的交接区域能很好地拼接在一起，交接区域并无明显的错位。图8（第二列）中的第一张图、第二张图、第三张图、第四张是直接使用ICP算法进行拼接的效果图（对应 0°、90°、180°、270°视角）。由于ICP 算法一般应用于同一面的点云配准，对本文前部点云和后部点云这样具有局部重叠区域且重叠区域比较少的情况，导致配准的精度不高。在图8（第二列第一张图）中后部点云已经开始发生偏移，图8（第二列第二张图）中前部点云和后部点云的交接区域有明显的错位。图8（第二列第三张图）中后部点云已经跟的前部点云有穿模现象，图8（第二列第四张图）中前部点云和后部点云交接区域穿模更加明显。

图9 打印机配准效果图

图9 第一列为顺序配准对打印机进行配准的效果图。用2.1 小节采集到的点云，以1→0→2→4→3→5按圆周顺序两两使用ICP 算法进行配准得到的效果图。在顺序配准的正面视图（图9 第一列第一张图）可以看到前部点云配准获得不错的配准效果。但是由于点云2 和点云4 缺少特征，点云2 和点云4 配准误差开始增大，从而导致点云3 的配准精度低下。在反面视图（图9 第一列第三张图）后部点云的右边部分已经向前部点云倾斜的。

图9 第二列为ICP 算法对打印机前部点云和后部点云配准的效果图。在左视图和右视图中（图9 第二列第二张图、第二列第四张图）明显看出前部点云和后部点云的圆盒的交接区域已经出现上下错位，并且正面效果图（图9 第二列第一张图），前部点云看出已经向右边偏斜。图9 第三列是使用本文方法（2.4.1 小节到2.4.2 小节）对打印机前部点云和后部点云配准的效果图，可以看到前部点云和后部点云配准的交接区域能很好地拼接在一起，交接区域并无明显的错位。

从以上实例可看出，本文方法利用圆盒点云作为特征点进行配准，依赖于圆盒稳定的几何特征，配准效果明显比ICP 算法好。

4 结语

本文提出了一个Kinect V2 闭合多视角三维点云的配准方法。首先，将建模物体放在旋转圆盒上，利用Kinect V2 对建模物体进行每隔60°进行一次点云数据采集，获得一个含有6 个点云的有序而且闭环的点云序列。其次，对建模物体0°到180°视角范围内的3个点云（180°到360°角范围内的3 个点云）进行配准生成前部点云（后部点云）。再次，用基于圆盒特征和小型包围盒约束的方法对前部点云和后部点云进行粗匹配。最后，用基于圆盒特征和SVD 奇异值刚性变换矩阵评估法对前部点云和后部进行细匹配。理论分析和实验结果表明，所提出的方法克服了多视角点云配准的误差累积问题，该配准方法提高了三维点云的配准质量，为在点云上进一步进行曲面重建创造了良好的条件。