结合改进的损失函数与多重范数的人脸识别

张飞翔，余学儒，何卫锋，李 琛

1.上海交通大学 电子信息与电气工程学院 微纳电子学系，上海200240

2.上海集成电路研发中心有限公司AI部，上海201203

1 引言

基于卷积神经网络的人脸识别是近年来机器学习领域非常热门的研究方向，其涉及了机器视觉、模式识别、神经网络等多学科内容[1]。卷积神经网络包含了网络模型的构建、损失函数的选取、特征相似度等问题。残差神经网络[2]（Resnet）的出现解决了传统深度神经随着网络加深退化的问题，修改损失函数和特征相似度成为优化人脸识别模型的研究热点。

Softmax损失函数在深度神经网络中被广泛使用[3]，先将分类结果映射到指数域上后再归一化，收敛速度快，但因只考虑了分类正确与否，未能设置类内约束，导致最终的特征提取效果不佳。权重与特征归一化Softmax（W&F-Norm Softmax）[4-5]去掉了Softmax 的偏置，之后将最后一层卷积层输出和全连接层权重L2范数归一化，减少了网络参数，并且将损失函数引入到了余弦域中。文献[6]提出了一种添加余弦裕度的损失函数（Cosineface），相比特征与权重归一化Softmax，Cosineface添加了类内约束，提升了人脸识别率，但存在着算法收敛较慢的缺点。文献[7]提出了一种添加角度裕度的损失函数（Arcface），相比Cosineface，Arcface 在几何性质上有更好的解释性，并且文中在不同阶段的角度约束时对损失函数的贡献进行了量化与论证。但Arcface 涉及到余弦函数计算，计算过程较为复杂。

目前基于余弦域损失函数的人脸识别算法模型收敛速度较慢，类内距离变化幅度较小。与训练阶段余弦域损失函数相匹配的测试阶段，应当使用L2范数归一化特征，再计算特征差的L2范数衡量特征间相似度[8]。但对于一些异常数据单单依靠L2范数时特征相似度信息太少，无法达到正确分类。

本文根据神经网络训练时收敛的条件，针对添加类内约束后收敛变慢，提出了一种斜率可变的余弦裕度损失函数，在训练过程中与较为常见的损失函数进行人脸识别效果对比，并且在最佳模型上使用多重范数来代替L2范数衡量特征相似度，探讨斜率可变的余弦裕度损失函数在提升收敛速度和降低类内距离上的优势，以及多重范数在提升识别率上的效果。

2 损失函数的演变过程及本文改进

本文使用的神经网络的训练流程如图1所示，人脸图片先经过卷积层转变为特征向量，再通过一层全连接层后计算损失函数。神经网络的训练即寻找损失函数最小时对应的参数最优解。近年来，损失函数基于Softmax有很多改进算法，其中包括W&F-Norm Softmax、Cosineface、Arcface等。

2.1 Softmax

Softmax最常用的损失函数之一，该函数的定义如下：

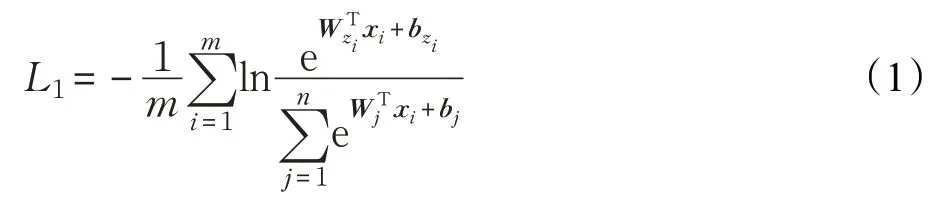
其中，m表示在训练过程中batch的大小，n表示训练集的类别个数，xi表示第i个样本的特征值，该样本属于zi类，W ∈Rd×n表示最后一层全连接层的权重，b ∈Rn表示最后一层全连接层的偏置。在卷积神经网络中，一般将最后一层卷积层的输出值作为特征x，经过全连接层编码WTx ∈Rn之后进入Softmax 层，将特征转化为属于各个类的概率值。

2.2 W&F-Norm Softmax

为了简化，一般将Softmax 的全连接层的偏置设置为0，且为了将更多的分类信息集中体现在角度域上，将特征和权重进行L2范数归一化处理，计算两者的乘积，就得到了该特征与权重之间夹角的余弦值，即

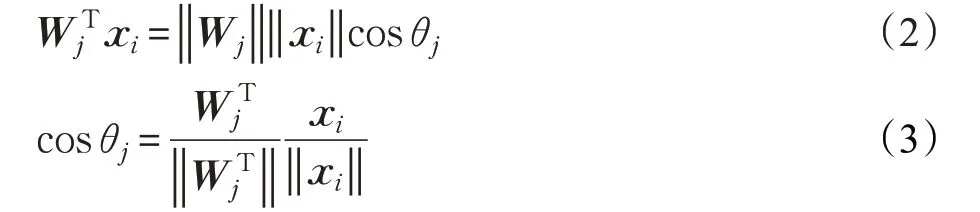
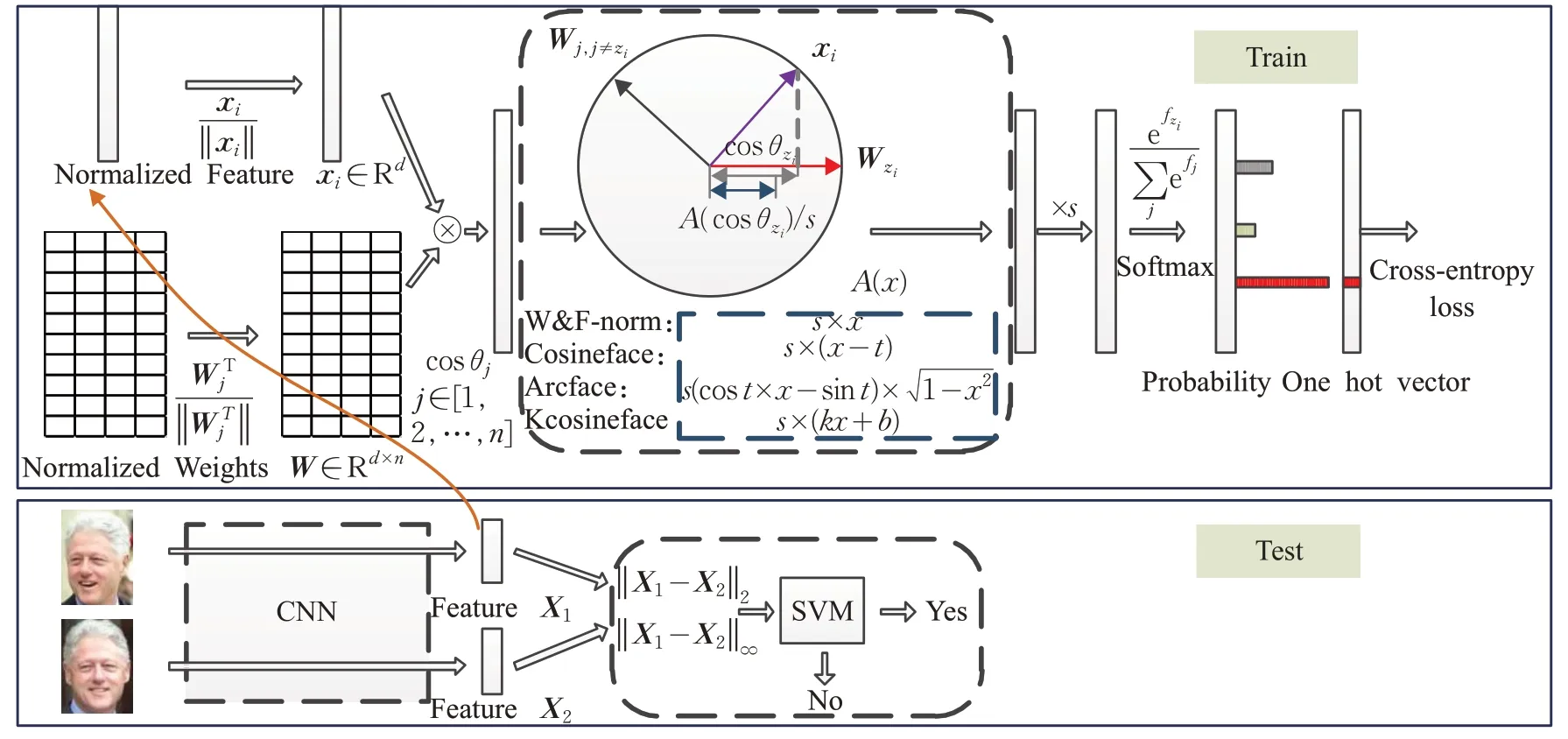
图1 人脸识别模型

经过特征和权重归一化之后，分类边界只与角度有关，训练神经网络时通过优化损失函数将对应角度缩小。文献[9-10]解释了归一化对于特征提取的作用。由于在归一化之后，特征空间被压缩到单位超球面上，导致损失函数无法优化到接近于0，故添加尺度因子s将特征空间扩大。

2.3 Cosineface

W&F-NormSoftmax 只强调分类正确与否，对类内距离和类间距离没有设置约束。Cosineface通过添加角度余弦裕度，使得类内特征更加紧密，从而变相增加了类间距离，即

其中，t为角度余弦裕度。

2.4 Arcface

相比Cosineface，Arcface对类内的约束具有更加直观的解释性。通过设置角度裕度t ，使得特征与权重之间的角度大于其真实值，这使得优化条件变得更加苛刻，即

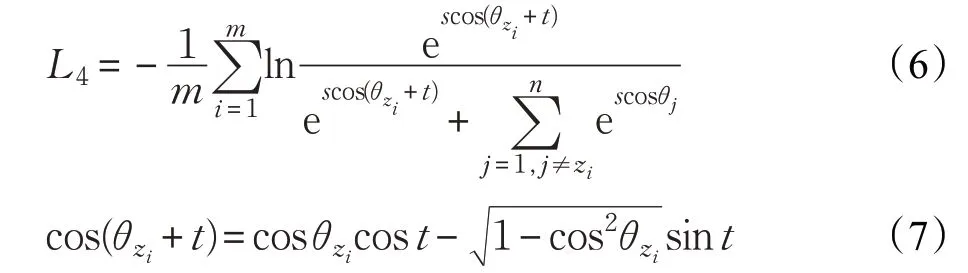
根据式（6）、式（7）可以看出Arcface 是余弦域损失函数的一种情况。

2.5 改进的损失函数Kcosine

令y=cosθ∈[-1,+1]，损失函数为：

其中，A(s,yi)为特征与标签对应的权重之间的角度余弦函数，B(s,yi)为特征与其他权重之间的角度余弦函数。为了满足优化条件，损失函数一般需具有以下几个性质：

为了简化并满足性质（2），将A和B设定为指数形式，即

若要满足性质（1）、（3）、（4），只需满足式（11）、（12）即可。

根据式（11）、（12）构造函数A(s,yi)=s(kyi+b)，其中k大于0。添加余弦裕度，需要使得：

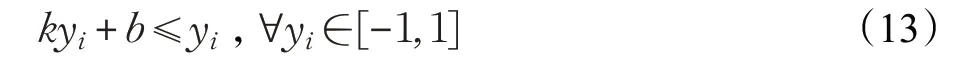
即，b≤k-1。如图2 所示，改进的kcosine 具有更多的变化形式，是对Cosineface 的扩展，相比Arcface 不需要复杂的角度余弦变换和计算。

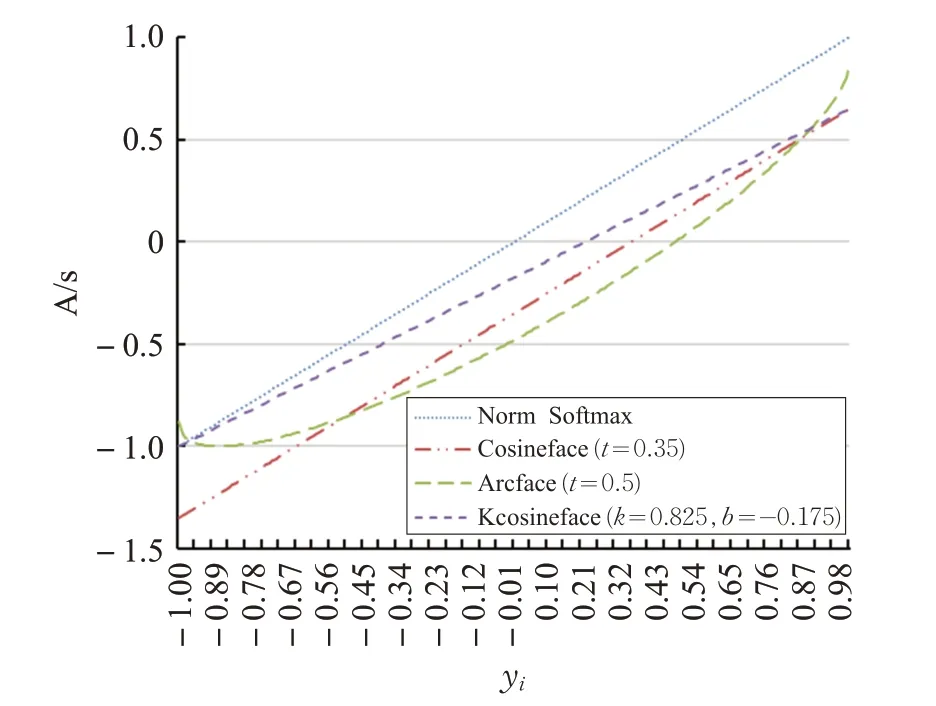
图2 A/s曲线

3 特征相似度衡量

在人脸识别模型测试时，通常使用计算特征差的L2范数来计算相似度，本文采用多重范数方法对其改进，流程如图1所示。

3.1 L2范数

人脸识别通常可以分为两个部分：特征提取和特征相似度衡量。目前较为流行的特征提取办法是经过分类训练的深度神经网络的卷积层部分，由于本文采用余弦域相关的损失函数，故在特征相似度衡量时先将特征进行L2范数归一化处理，再计算特征差的L2范数评价其相似程度，这样处理的好处在于通过L2范数可以评价余弦相似度。

L2范数定义如下：

其中，A 和B 为两个n维向量。设定阈值，根据式（15）比较L2范数和阈值的大小，判定两个特征是否来自同一个人。

3.2 多重范数

使用MobileFaceNets[11]网络作为特征提取部分，L2范数作为衡量方法，6 000 组LFW[12]图片作为测试集（3 000组正类：相同ID，3 000组负类：不同ID，每组两张图片），根据10-fold 规则依次选取5 400 组作为训练集统计出最佳阈值，另外600组作为测试集测试阈值分类效果。图3 中（a）图、（b）图、（c）图记录了3 份测试集的L2范数的平方值（1～300 为正类，301～600 为负类，图中横线为通过训练集得到的最佳阈值），观察得知，在阈值附近，存在一些异常点被误判，不能通过一维阈值达到很好的线性可分。

假设在阈值附近存在两个不同ID 的特征满足式（16）、（17）：

其中，n表示特征维度。即存在分量在L2范数计算时占据主导作用，但并不能通过阈值将其判定为负类，基于这个假设，可以通过计算特征差值的L∞范数即最大值，将该组特征判定为负类。图3中（a）图、（b）图、（c）图所示，L∞范数与L2范数存在相关关系，且在正类和负类的L∞范数的散点图呈明显阶梯状，故选取L∞范数特征作为L2范数的辅助特征。

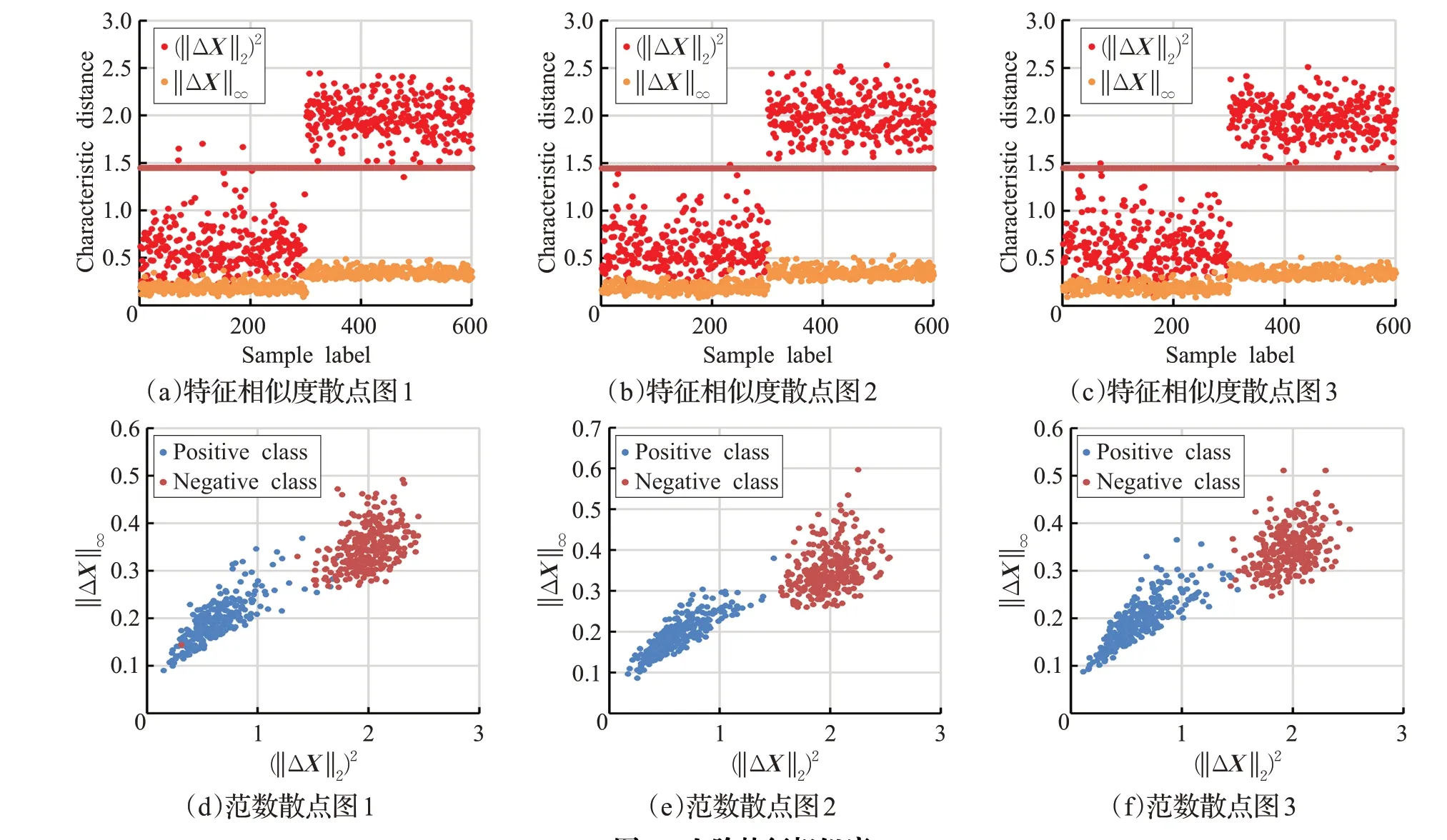
图3 人脸特征相似度

构建新特征L，满足式（18）、（19）：

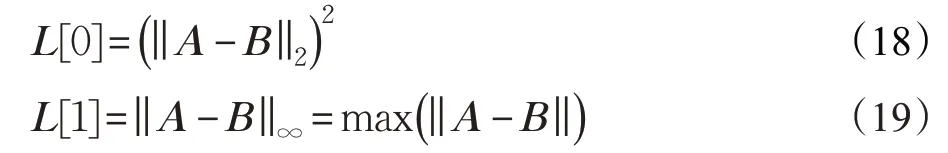
图3中（d）、（e）、（f）图分别记录了（a）、（b）、（c）图对应数据构建新特征的二维图，相比一维L2范数特征在分类策略上有更多的选择。本文采用SVM[13]对构建的新特征进行分类，核函数采用高斯核。

4 实验

为了证明改进损失函数和多重范数与SVM结合的有效性，本文首先根据相同的网络设置和环境，比较不同损失函数下模型训练后的人脸识别准确度。挑选出最佳模型，通过比较利用L2范数和利用多重范数+SVM的人脸识别准确率大小，证明新算法的优势所在。

4.1 实验所需数据库

本文采用MS-Celeb-1M-Arcface[14]数据集作为训练集，LFW、AgeDb[15]作为测试集。

4.1.1 MS-Celeb-1M-Arcface

在微软亚洲研究院公布的MS-Celeb-1M的基础上，文献[7]检查了所有图片特征与身份特征中心的距离，删除掉了距离身份特征中心较远的干扰项，并且对距离身份特征信息较近的图像和其身份做了对比，即在类内和类间距离上排除了噪声。该数据集包含了85 164 个ID，总共有380 4847张人脸。

4.1.2 LFW

从LFW数据集中随机抽选了6 000对图片，其中相同身份和不同身份的图片对各占一半，图4显示了LFW数据集的部分图片。该数据集主要用来测试人脸识别算法的准确率，计算公式为（正确判断相同身份的个数+正确判断不同身份的个数）/6 000。

图4 LFW数据库部分人脸

4.1.3 Agedb

AgeDb 包含了不同ID 的不同年龄段的照片，涵盖年龄范围为3～101岁。采用和对LFW相同的处理方式，随机抽选6 000对照片，3 000对来自相同ID，3 000对来自不同ID，通过对比验证方法测试人脸识别准确率。图5为Agedb数据库中的部分图片。

图5 Agedb数据库部分人脸

4.2 实验设置

实验使用两个GPU 核，其型号为NVIDIAGM204-GL（Tesla M60），每个核显存大小为8129MiB。在Linux环境下利用MxNet 库完成实验模型构建以及新算法实现。

使用SE_LResNet100_IR[7]网络训练人脸识别模型，最后一层卷积层输出维度为512，batch大小为80。

4.3 实验结果

4.3.1 损失函数优化结果

为了比较使用不同损失函数在训练过程中的收敛速度，每2 000个batch采样一次，使用LFW和AgeDb测试采样模型的识别准确率。经测试，在经过64 000 个batch之后，算法进入平稳期，识别率出现震荡且增长缓慢，故本实验只比较了64 000 个batch 内模型的训练情况。实验结果如图6、图7 所示，在余弦域损失函数中，权重-特征归一化后的Softmax 损失函数没有添加余弦惩罚效果较差，kcosine(k=0.825,b=-0.175)相比其他余弦域损失函数识别率增长速度较快且更加平稳，在经过64 000个batch后识别率最高。

图6 在LFW下准确率变化曲线

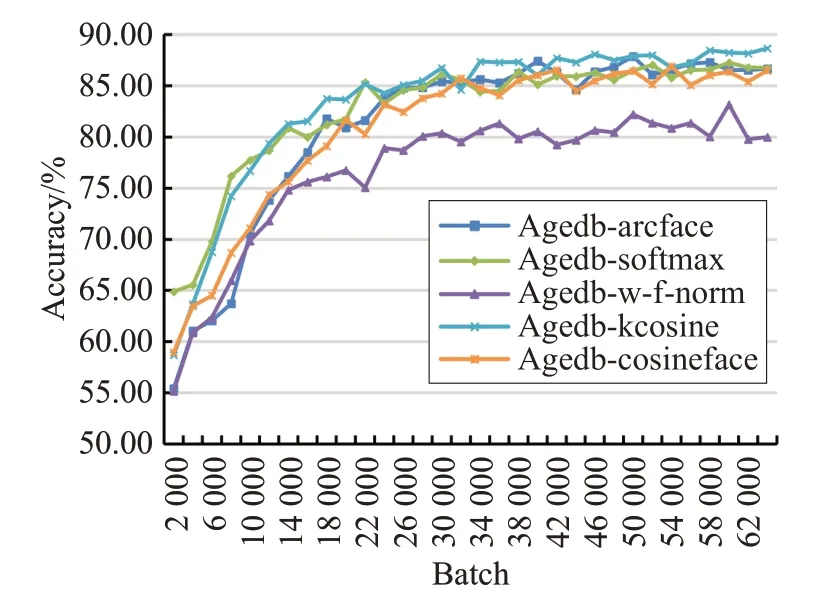
图7 在Agedb下准确率变化曲线

图8 在LFW下平滑后的准确率变化曲线

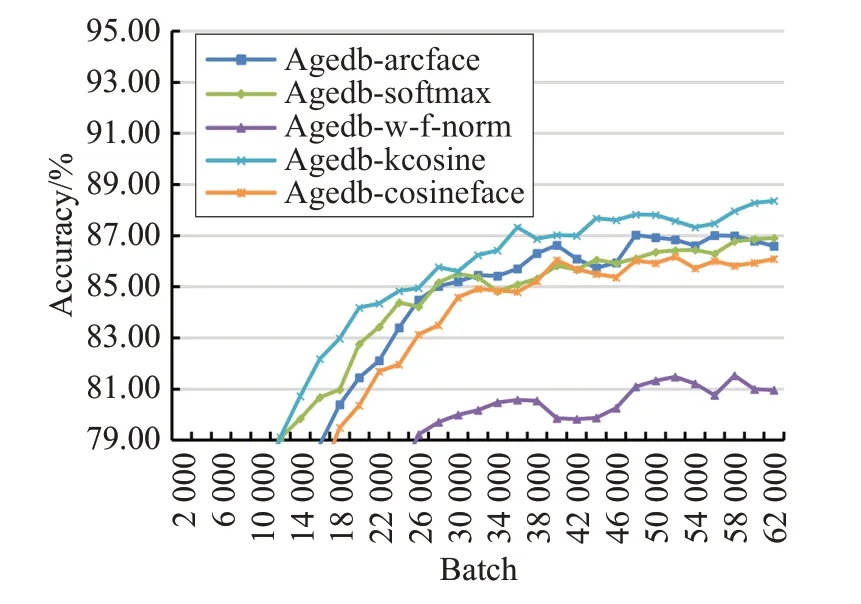
图9 在Agedb下平滑后的准确率变化曲线

为了减少干扰，将所有曲线进行窗口为3的平滑滤波处理，如图8、图9所示，可以看出kcosine损失函数相比Softmax，在LFW 数据集上识别率增长平稳，并且在64 000 个batch后的识别率更优。在Agedb 数据集上曲线震荡都较为明显，但kcosine要明显优于Softmax损失函数训练模型的识别效果。

表1 比较了以上所有算法经过64 000 个batch 训练之后在LFW 和Agedb 数据集上的识别率，可以看出经过改进的kcosine算法识别效果较好。

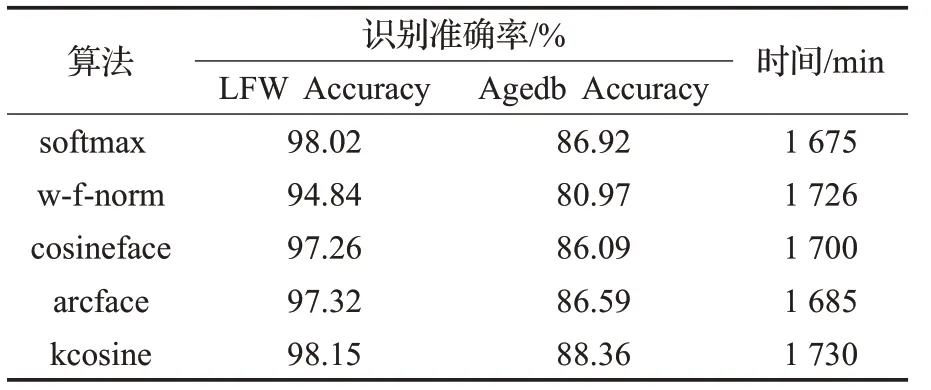
表1 LFW和Agedb数据库下的识别率

将6 000对LFW人脸图片作为输入，经过不同batch个数下的模型输出后，进行L2范数归一化，最后分别统计3 000 对正类和3 000 对负类的L2范数均值衡量该模型输出特征类内距离和类间距离。kcosine 中参数k为0.825、b=-0.175，其目的在于当角度余弦为-1时kcosine和w-f-norm softmax保持一致，惩罚力度为0，当角度余弦为+1 时kcosine 和cosineface 的惩罚力度保持一致。即kcosine随着夹角的增大，惩罚力度也逐渐增加，这样可以避免在优化过程中当分类效果不佳时惩罚的冗余。

如图10、图11所示，kcosine能够将类内距离快速降低，且类间距离也相对较低，在64 000 个batch 训练下，kcosine 相比其他两种算法不仅可以更好地分类，还能在类内距离和类间距离上得到优化。

本文中，人脸识别模型训练时使用的余弦域损失函数的时间复杂度都为O(n),n为训练集的大小。在训练过程中，训练60 000个batch所使用的时间如表1所示，由于涉及到GPU 调度和交互，不同算法所用时间的长短关系可能存在偏差，但基本都在同一量级上。kcosine在保证人脸识别率稳定快速增长的同时，用时没有明显增加，并且在训练用时相同时，kcosine相比于其他几种算法具备人脸识别率较高的优势。

4.3.2 多重范数特征优化结果

采用kcosine损失函数优化后的模型和Mobilefacenet模型，根据10-fold 规则分别测量在LFW 和Agedb 数据集下不同特征衡量方法的识别率。由表2 数据可以得出使用构造出的多重范数特征衡量方法可以使识别率均值提升0.1%左右，并且降低了识别率标准差，有更加稳定的泛化能力。

在识别过程中，由于只侧重于实时识别效率，故不考虑欧式距离阈值计算和SVM 训练的用时。经测试，每组图片使用欧式距离分类的平均用时为7.92×10-6s，使用多重范数+SVM 分类的平均用时为1.23×10-5s。相对于欧式距离，多重范数的使用使得用时增加了55.3%，但根据人眼视觉暂留机制，10-6s 量级的延时对人眼体验来说是几乎没有影响的。

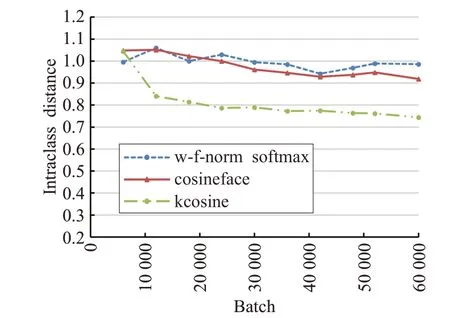
图10 类内距离变化趋势图

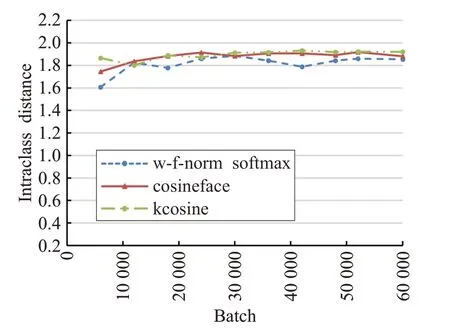
图11 类间距离变化趋势图

表2 LFW和Agedb数据库下的识别率

5 结束语

针对余弦域损失函数的类内约束，本文提出了基于添加斜率因子的余弦损失函数，比较了多种余弦域函数的优劣并与常用的Softmax 作比较，分析了几种算法在优化类内距离和类间距离的作用，改进的损失函数在收敛速度和优化特征类内距离上均能做出改善。并且针对L2范数在衡量特征相似度上存在的不足，提出了多重范数算法，利用L∞范数和L2范数结合的方式构造新特征，实现特征升维的效果，通过SVM 将新特征分类，实验证明，构建的新特征在SVM上有较好的分类效果，优化了人脸识别模型输出个别特征不佳的缺陷，在人脸识别率提升空间不大的情况下能够将其提升0.1%，并且使算法的泛化能力更加稳定。