基于时域和频域分析的滚动轴承故障诊断

程秀芳，王鹏

(华北理工大学 机械工程学院，河北 唐山 063210)

0 引言

滚动轴承是机械设备中最为常见的部件之一，轴承的运行状态直接影响设备的整体性能。当滚动轴承各元件表面出现点蚀、剥落等局部损伤故障时，就会激起系统的高频固有振动[1]，如果是大型设备的滚动轴承发生了故障，则有可能造成巨大的财产损失甚至人员伤亡[2]。因此，对滚动轴承进行故障诊断，检测滚动轴承的运行状况是十分必要的。

目前，对滚动轴承进行故障诊断的方法主要分为时域分析、频域分析、时频分析[3]。虽然滚动轴承的故障信号属于非平稳信号，但信号的时域、频域分析也是必不可少的基础方法。信号的时域指标分析具有直观、准确的特点，当信号异常时，有些时域指标会出现明显的变化。频域分析是将一个复杂信号分解为简单信号的叠加，易于理解且物理意义明确[4]。因此，时域分析和频域分析在滚动轴承的故障诊断中占有重要地位。

1 滚动轴承的故障数据

该项研究采用美国西储大学滚动轴承实验中心6205 SKF轴承的实验数据作为故障分析的依据，故障是由电火花加工出的单点故障，测试轴承连接在电机上，使用加速度传感器测试轴承的振动信号，电机转速为1 721 r/min，采样频率为12 kHz。表1所示为6205 SKF滚动轴承故障数据。

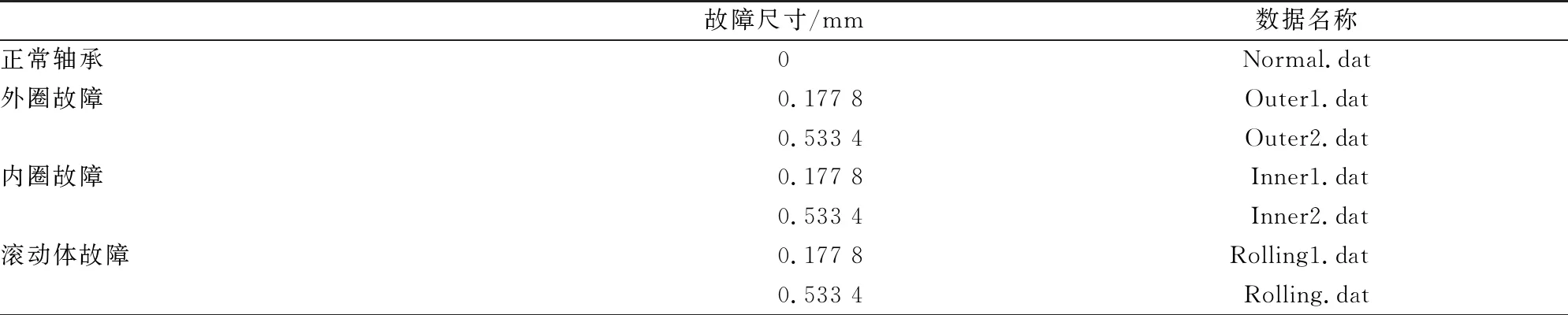
表1 6205 SKF滚动轴承故障数据

6205SKF轴承的结构参数如下：滚动体直径d=7.94 mm；节圆直径Dm=39.04 mm；滚动体的个数Z=9；由此可以计算出轴承外圈故障特征频率fo=102.82 Hz，内圈故障特征频率fi=155.33 Hz和滚动体故障特征频率fg=119.43 Hz，轴的转频fr=28.68 Hz。

2 滚动轴承故障信号的时域分析

时域分析可以从时域波形和时域指标2个方面观察信号的特点。从时域波形可以直观地看出振动信号随时间的变化情况。而时域指标中的峭度因子，峰值因子，脉冲因子可以较好地反映轴承故障信号中是否存在冲击脉冲[5]。

2.1 时域波形分析

图1是6205轴承外圈故障的振动信号，其中，图1(a)、图1 (b)、图1 (c)分别是正常轴承、外圈故障尺寸为0.177 8 mm和尺寸为0.533 4 mm的轴承振动信号的时域波形。如图1(a)所示正常轴承的振动信号冲击特征微弱，且相邻冲击时间间隔没有规律，不是轴承局部损伤的征兆特征；当外圈有故障时，如图1(b)、图1(c)所示，振动信号出现明显的冲击成分，如图1(b)冲击幅值大约为正常轴承幅值的10倍，如图1(c)冲击幅值大约为正常轴承幅值的25倍，表明轴承的故障尺寸越大，信号中的冲击现象越明显且振动幅值越大。

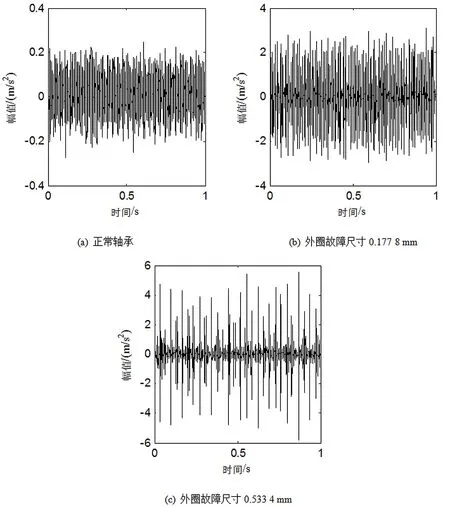
图1 6205轴承外圈故障的振动信号

2.2 时域指标分析

表1中7组滚动轴承故障数据的峭度因子、峰值因子、脉冲因子3个时域指标的计算结果，如表2所示。

表2 6205轴承外圈、内圈、滚动体故障信号的时域指标

2.2.1外圈故障分析

由表2可知，正常轴承的峭度因子为2.61，峭度因子的增大表明信号中冲击成分增多，偏离了轴承正常运转状态。当外圈故障尺寸分别为0.177 8 mm和0.533 4 mm时，峭度因子分别是正常轴承的3倍和9倍，表明故障尺寸越大产生的冲击现象越严重。峰值因子定义为峰值与均方根值之比，峰值因子的值越大表明信号中的冲击现象越严重，即轴承的损伤越严重。当外圈故障尺寸分别为0.177 8 mm和0.533 4 mm时，峰值因子分别是正常轴承的1.3倍和2.8倍，脉冲因子分别是正常轴承的1.7倍和4.7倍。

由上述数据分析可知，轴承外圈故障发生时，这3个指标均有明显的变化，外圈故障尺寸越大，指标值也越大，由此可初步判断轴承出现故障。内圈故障分析，与外圈故障情况类似。

2.2.2 滚动体故障分析

由表2可知，当滚动体发生故障时，随着滚动体故障尺寸的变化峭度因子几乎没有明显的变化。当故障尺寸为0.177 8 mm时，脉冲因子和峰值因子与正常轴承相比几乎没有增加，当故障尺寸为0.533 mm时，脉冲因子和峰值因子比正常轴承增加了约0.5倍。因此当滚动体故障尺寸较大时，可以使用脉冲因子和峰值因子来判断轴承的故障；而当滚动体故障尺寸较小时，3个指标均无法有效地诊断出轴承的故障。因此，时域指标无法有效地判断出滚动体的故障。

3 滚动轴承故障信号的频域分析

时域分析能够直观地观察滚动轴承振动信号的幅值大小和变化规律，但是不能提供包含频率关键信息的振动信号。使用傅里叶变换可以将信号从时域转换到频域，再根据轴承内圈、外圈、滚动体的故障特征频率来识别故障的部位。

3.1 滚动轴承振动信号的特点及故障诊断理论

滚动轴承的振动信号是在轴承座上检测的，当轴承有局部损伤故障时，振动信号包括简谐振动(滚动体通过负载区产生)、周期性冲击(损伤点通过其他元件表面产生)、背景噪声及信号传播过程的其他信息。其中周期性冲击及相邻冲击的时间间隔是轴承具有局部损伤的判定依据。滚动轴承的故障信号处在2个频段(如图2所示)，低频段(<2 kHz)，这个频段有冲击成分，通常包括轴、轴承和齿轮啮合振动；高频段(2～6 kHz)，这个频段是轴承损伤引起的固有频率的衰减震荡，一般只有轴承的故障信号[6]。因此，可以采用高频段作为轴承的故障诊断频段。

由于滚动轴承的故障特征频率很低，要想从高频段中找出低频的故障特征，需要使用共振解调理论。该研究采用Hilbert包络分析来提取高频振动信号中的低频调制信号，再对获得的低频调制信号进行功率谱分析，最后根据功率谱峰中心频率来判断故障的部位。

一个连续时间信号x(t)进行Hilbert变换如下：

(1)

信号x(t)的解析信号可以表示为：

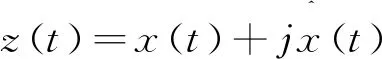
(2)

对解析信号进行傅里叶变换可得：

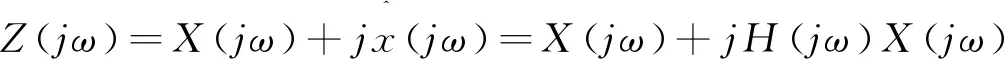
(3)

即：

(4)

此时便实现了轴承故障信号的解调。

3.2 外圈故障分析

将表1的振动信号，经过抗混叠滤波后进行快速傅里叶变换(FFT)得到如图2所示频谱图。其中，图2(a)、图2(b)、图2(c)分别是正常轴承、外圈故障尺寸为0.177 8 mm和故障尺寸为0.533 4 mm的轴承振动信号形成的频谱图。由图2(a)可知，正常轴承的冲击振动主要在0～1 kHz的低频段且能量较小，其冲击振动在1 000 Hz处出现瞬态简谐振动，这是滚动体通过负载区产生的正常振动，和轴承的故障无关。由图2(b)、图2(c)可知，当轴承外圈出现故障时，冲击振动主要集中在2～4 kHz高频段。

图2的频谱图并不能反映出轴承的故障特征频率，采用Hilbert包络解调算法提取低频调制信号，并且进行功率谱分析，如图3所示。图3(b)、图(c)均显示出外圈故障频率 (103 Hz)处有明显的谱峰值，并且，当外圈故障尺寸为0.177 8 mm时，转频 (28.68 Hz)的幅值为0.02；当外圈故障尺寸为0.533 mm时，转频 (28.68 Hz)的幅值为0.07，并且出现多阶转频的倍频且幅值较大。可判断是轴承的外圈存在故障。

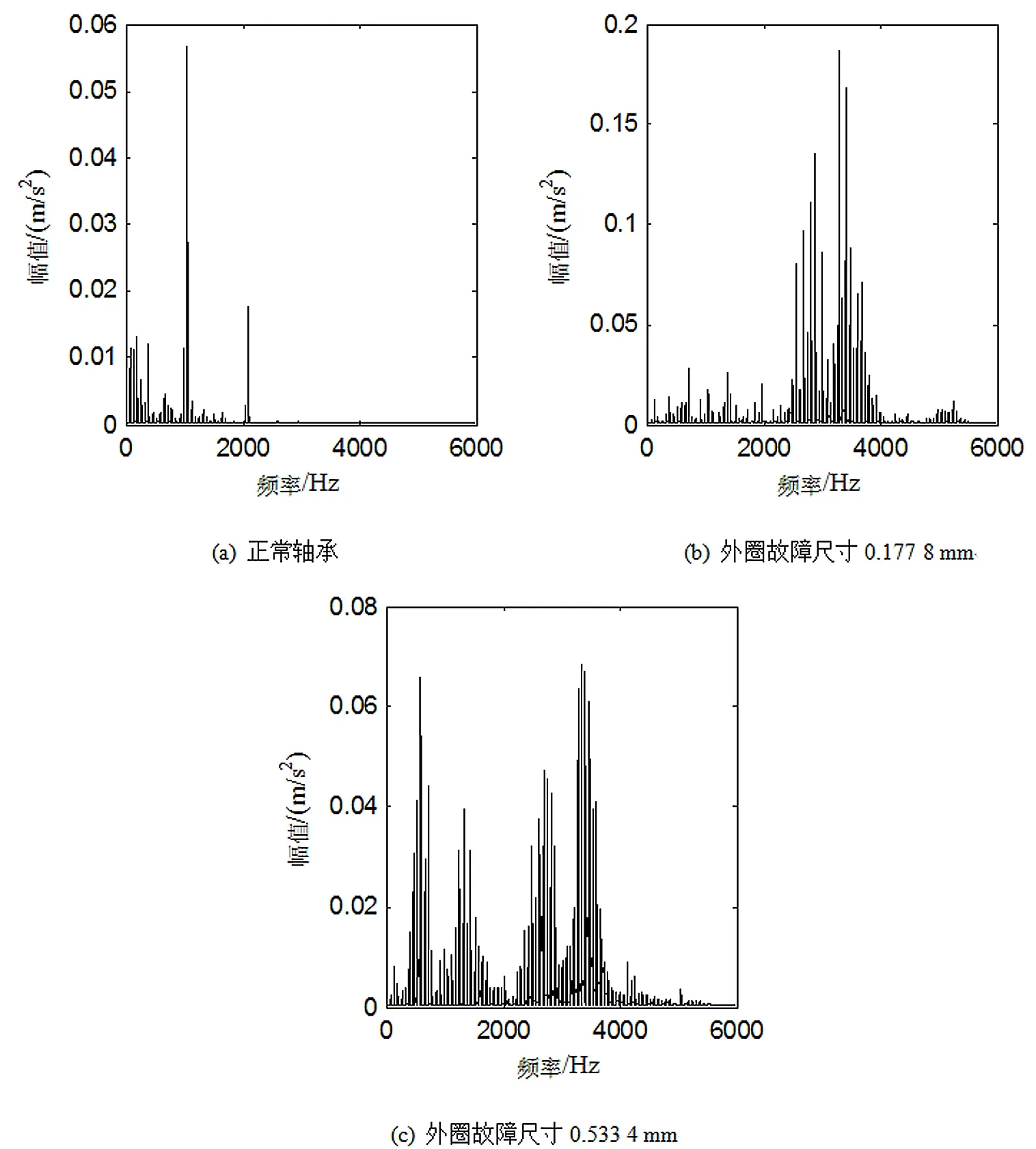
图2 6205轴承外圈故障信号的FFT谱图

3.3 内圈故障分析

图4是表1对应的6205轴承内圈故障振动信号的频域图，图5是内圈故障信号的Hilbert包络解调后的信号功率谱图。图5(a)、图5(b)均显示出内圈故障频率 (155.33 Hz)附近有明显的谱峰值，当内圈故障尺寸为0.177 8 mm时，在156 Hz处幅值为0.024；当内圈故障尺寸为0.533 4 mm时，在156 Hz处幅值为0.069，幅值增加了1.87倍，由此可以判断轴承内圈出现故障。

图5 6205轴承内圈故障信号的功率谱图

3.4 滚动体故障分析

图6是表1对应的6205轴承滚动体故障振动信号的频域图，图7是滚动体故障信号的Hilbert包络解调后的信号功率谱图。

图6 6205轴承滚动体故障信号的FFT谱图

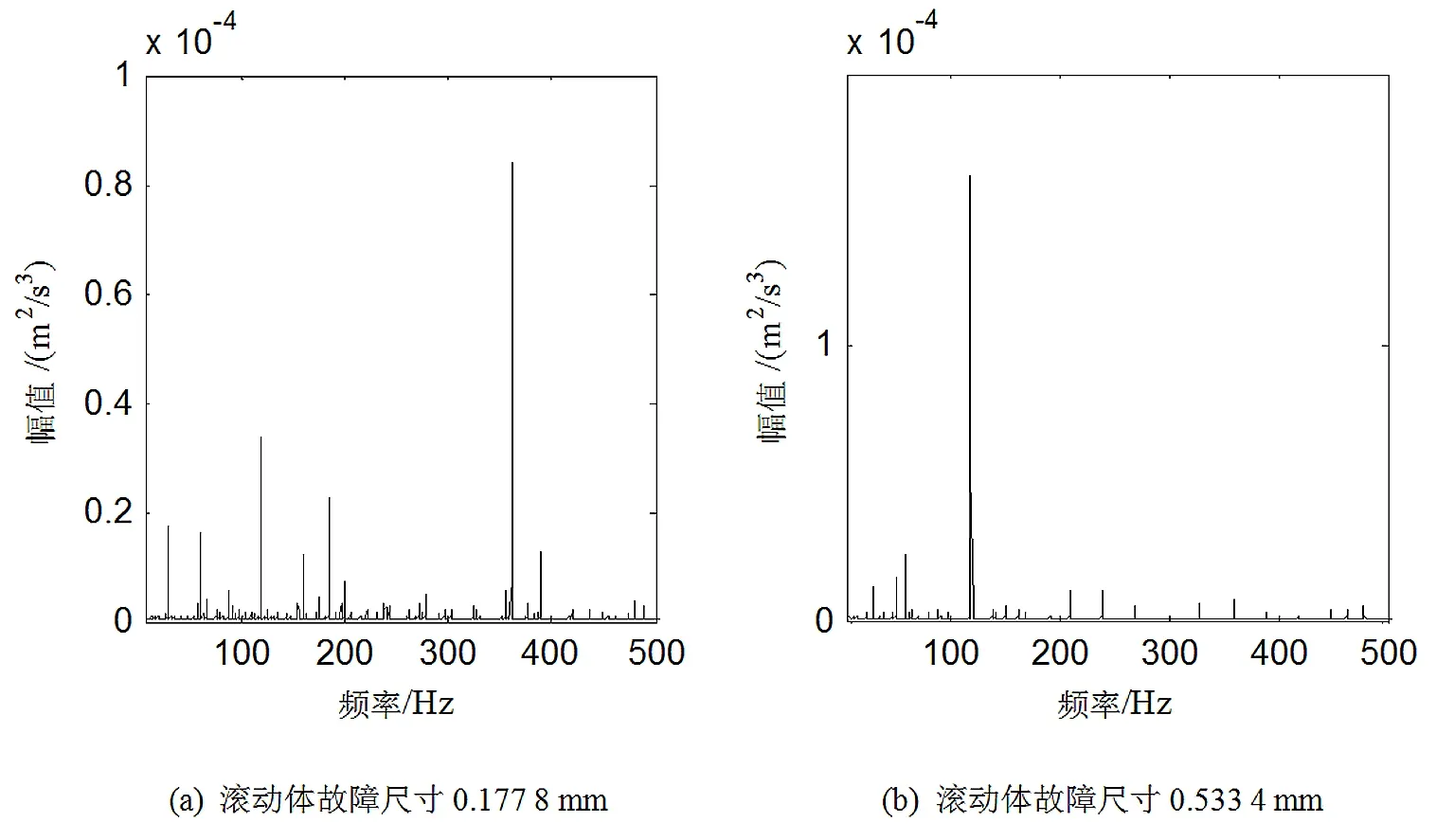
图7 6205轴承滚动体故障信号的功率谱图

图7(a)、图7(b)均显示出滚动体故障频率fg(119.43 Hz)附近有明显的谱峰值，当滚动体故障尺寸为0.177 8 mm时，在118 Hz处幅值为0.000 035；当滚动体故障尺寸为0.533 4 mm时，在118 Hz处幅值为0.000 17，其幅值增加了3.86倍，由此可以判断轴承的滚动体出现故障。但是，当滚动体发生故障时，振动的幅值相比外圈和内圈故障的振动幅值小得多，因此，滚动体发生故障更加不容易检测。

4 结论

(1)对于外圈固定、内圈旋转的滚动轴承，外圈的损伤会产生明显的冲击特征；内圈和滚动体损伤只有在通过载荷区及滚动体与滚道接触时，才有明显的冲击，并且内圈和滚动体损伤引起的振动传递到轴承座会损耗能量，尤其是滚动体的故障信号较微弱。

(2)时域指标中的峭度因子、峰值因子和脉冲因子可以较好地反映轴承故障信号中是否存在冲击脉冲，当时域指标增大时，可以初步判断轴承出现故障，但是故障具体发生的部位却无法判断。

(3)滚动轴承有局部损伤故障时，高频段会产生由于轴承损伤引起的固有频率衰减震荡的特征。因此，采用Hilbert包络分析来提取高频振动信号中的低频调制信号，并对低频调制信号进行功率谱分析，根据功率谱峰中心频率和轴承故障频率的对比，可以有效地判断出故障的部位。