四旋翼姿态的反步滑模RBF 网络自适应控制

李 众，沈炜皓

（江苏科技大学电子信息学院，江苏 镇江 212003）

0 引言

四旋翼无人机具备灵活性强、能在恶劣环境中飞行和易操控等优点，成为近年来军事和民用领域的研究热点。但是四旋翼的欠驱动、耦合性强、易受干扰影响等特性，使得设计出性能良好的控制器富有挑战。姿态控制器是飞控系统的核心，其性能将直接决定飞行质量。

针对四旋翼无人机的姿态控制方法，若简化四旋翼无人机系统模型，可利用LQR［1］、PID［2］等线性控制方法设计控制器，但其控制性能较差。针对此问题，用反步控制［3］、滑模控制［4］、神经网络控制［5］等非线性控制方法能够提高无人机系统的性能。但是，当考虑模型中的不确定因素和外界干扰时，用上述的某一种控制方法不能达到良好的控制效果，通常将几种方法结合使用，达到取长补短的效果，使得四旋翼无人机系统的鲁棒性更强、飞行性能更好。文献［6］提出积分反步自适应控制方法，使得系统的自适应性得以提高。文献［7］针对反步法抗干扰性能较弱的问题，在反步控制基础上构造滑模面，设计反步滑模控制器。文献［8］运用滑模控制与RBF 网络控制相结合的方法，设计出具备较好抗干扰性的控制方法。文献［9］为提高四旋翼无人机对外界扰动的抑制能力，增强系统的自适应性，将自抗扰技术应用于四旋翼的姿态控制，结果表明该方法能取得预期效果。

针对外界存在常值扰动和变值扰动的四旋翼无人机姿态系统，反步滑模控制随干扰波动范围较大，抑制能力和鲁棒性有待提高。因此，根据文献［6-8］设计四旋翼无人机姿态的反步滑模RBF 网络自适应控制器。首先，在反步控制的基础上构造滑模面，设计出反步滑模控制器；其次，RBF 网络具备逼近和补偿扰动的性能，根据Lyapunov 方法得到RBF 网络权值的自适应律，最终将RBF 网络自适应控制和反步滑模控制相结合，使之具备更强的干扰抑制能力。

1 四旋翼动力学模型

图1 四旋翼结构图

四旋翼无人机是四输入六输出的欠驱动系统，其结构图如图1 所示。相邻两对旋翼的转向不同。通过调节4 个电机的转速，四旋翼产生横滚、俯仰、偏航运动。横滚角、俯仰角、偏航角分别用［Φ θ Ψ］T表示，四旋翼位移用［x y z］T表示。

四旋翼的非线性特性使得精确建模异常困难，所以为了方便建模求解，根据文献［1-3］，提出如下假设：1）四旋翼结构为刚体；2）四旋翼的严格对称；3）四旋翼的重心与中心一致。

运用Newton-Euler 法［10］对四旋翼建模，可得四旋翼动力学模型为［11］：

其中，Ωi（i=1，2，3，4）为4 个电机的转速，b 和d 分别为升力因子和阻力系数，Ωr=Ω1-Ω2+Ω3-Ω4。

2 控制器设计

若考虑外界存在扰动，可将四旋翼姿态系统方程表示为［8］：

其中，ΔΦ=MΦ/IX、Δθ=Mθ/IY、ΔΨ=MΨ/Iz，Mi（i=Φ，θ，Ψ）表示外界干扰力矩。

2.1 四旋翼姿态系统状态方程

可将四旋翼姿态系统动力学方程表达为：

结合式（3）～式（5）得：

表1 参数符号含义

2.2 反步滑模RBF 网络自适应控制器的设计

图2 控制结构图

由于式（15）中存在外界干扰ΔΦ，且ΔΦ的上界未知，所以利用RBF 网络自适应控制方法的逼近作用，实现对外界干扰的估计和补偿。

RBF 网络算法［12］如下：

其中，γ 为待设计参数，且γ>0。

定理 考虑外界存在扰动的四旋翼无人机姿态系统如式（3）所示，若系统误差由式（23）控制，RBF网络权值的自适应律如式（20）所示，则四旋翼无人机姿态系统将渐进稳定。

证明 为证明反步滑模RBF 网络自适应控制的稳定性，定义Lyapunov 函数V3为：

合理选取参数h1、c1、k1，可使|Q|>0，即保证矩阵Q 正定，从而保证V˙3≤0，所以控制系统是渐进稳定的。

同理，其他两个姿态角的控制量U3、U4的设计和证明与U2类似。

3 仿真对比与结果分析

利用MATLAB 进行姿态角轨迹跟踪实验，在相同姿态角初始条件下，分别施加常值干扰力矩和变值干扰力矩，比较反步滑模控制方法和反步滑模RBF 自适应控制方法的抗扰性能。系统参数［8］如表2 所示。

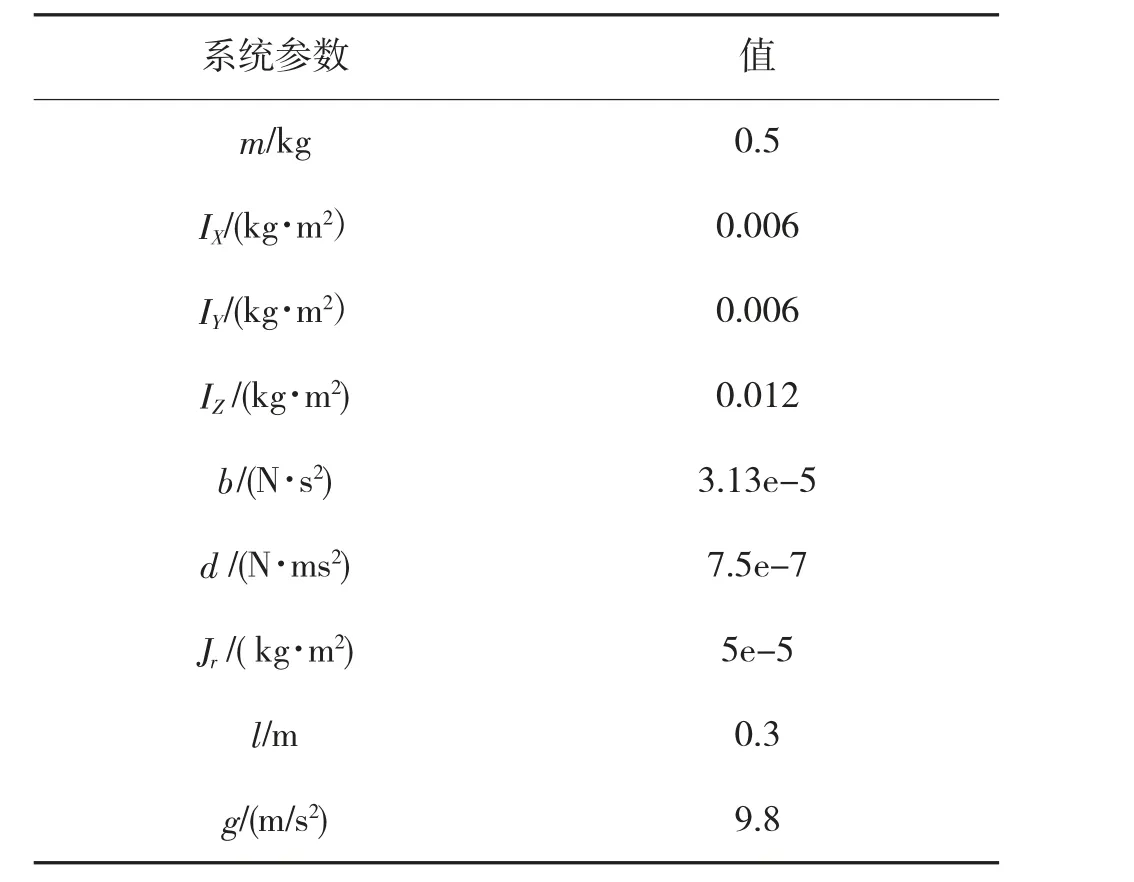
表2 系统参数

姿态系统的控制器参数选择如下：

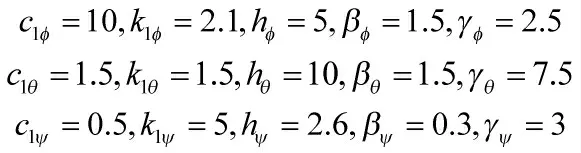
假设期望姿态角［ΦdθdΨd］轨迹均为5sin（t）。设置［Φ θ Ψ］初始值为［3° 3° 3°］，且其一阶导数为0，仿真时间为10 s。为了验证控制算法抑制干扰的能力，当t>0 s 时，在3 个姿态角通道分别施加0.3 N·m、0.3 N·m、0.6 N·m 的常值干扰力矩和0.3sin（t）N·m、0.3sin（t）N·m、0.6sin（t）N·m 的变值干扰力矩。

图3～图5 为在常值干扰力矩下，姿态角跟踪的控制效果对比。图6～图8 为在变值力矩干扰下，姿态角跟踪的控制效果对比。

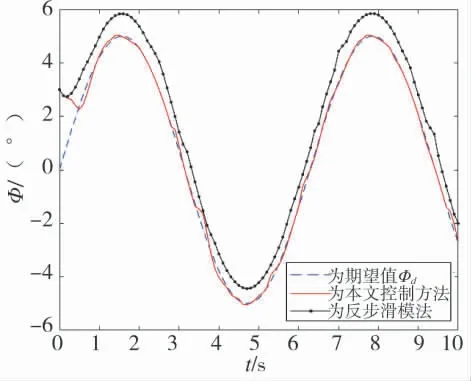
图3 常值干扰下横滚角追踪

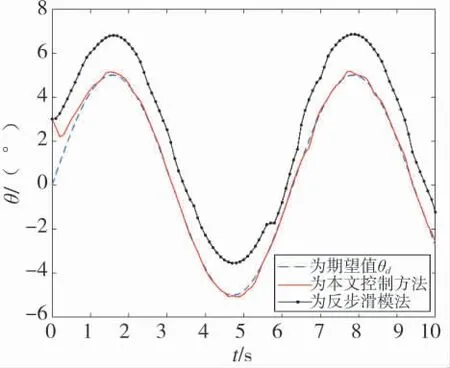
图4 常值干扰下俯仰角追踪

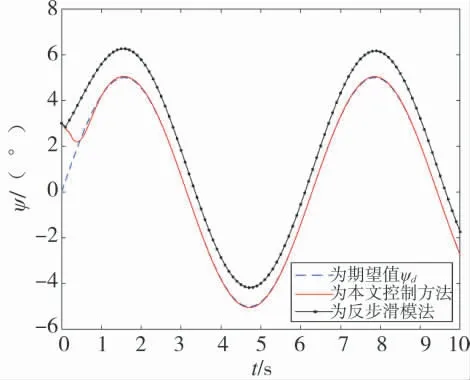
图5 常值干扰下偏航角追踪

由图3～图5 可知，当3 个姿态角通道分别存在0.3 N·m、0.3 N·m、0.6 N·m 的常值干扰力矩时，本文设计的控制算法对于期望姿态轨迹的跟踪效果较好，由于RBF 网络的逼近作用，及其对干扰的逼近补偿作用，该方法比反步滑模控制方法抑制干扰能力更强，追踪期望姿态角轨迹的误差较小，且超调量较小。

图6 变值干扰下横滚角追踪

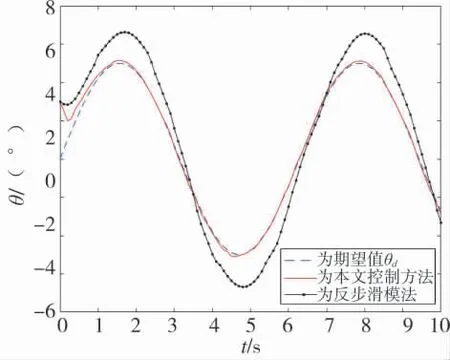
图7 变值干扰下俯仰角追踪

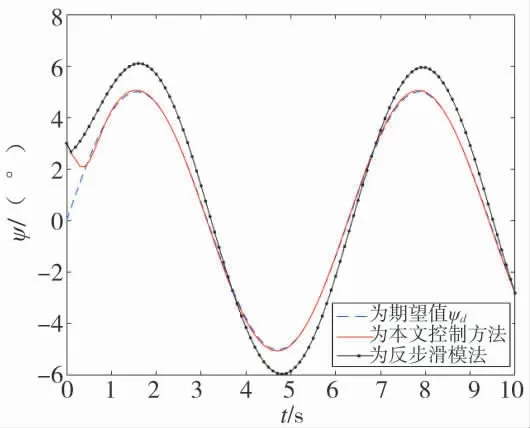
图8 变值干扰下偏航角追踪

由图6～图8 可知，当3 个姿态通道分别存在0.3 sin（t）N·m、0.3 sin（t）N·m、0.6 sin（t）N·m 的变值干扰力矩时，反步滑模控制方法不能很好地跟踪期望姿态轨迹，对时变干扰的抑制能力较差，随时变干扰的变化产生较大波动，存在较大超调量，最大跟踪误差达到1°。而本文设计的反步滑模RBF 网络自适应控制算法，对期望姿态轨迹的跟踪效果较好，由于RBF 网络具备万能逼近特性，对外界时变干扰能够进行有效估计和补偿，因此，随变值干扰产生的波动范围较小，超调量较小，角度跟踪误差保持在0.3°以内，能够较好地跟踪期望姿态轨迹，验证了该控制方法能够有效地抵抗和补偿变值干扰，抗干扰性能更强。

4 结论

针对外界存在常值干扰力矩和变值干扰力矩的四旋翼无人机姿态系统，本文将RBF 网络与反步滑模控制算法相结合，根据Lyapunov 方法构造RBF网络权值的自适应律，提出反步滑模RBF 网络自适应控制方法。该方法可应用于四旋翼无人机的姿态控制。通过Lyapunov 稳定性定理证明，基于反步滑模RBF 网络自适应控制算法的四旋翼无人机姿态系统是渐进稳定的。仿真实验结果可验证，当外界存在常值干扰力矩和变值干扰力矩时，相比于反步滑模控制算法，本文的控制方法抗干扰性能更强。