我国债券组合投资管理风险研究

张浩 河北地质大学

一、利率期限结构

利率期限结构是研究期限不同而其他特征相同的利率之间的关系。利率期限结构有三种理论：流动性偏好理论，期望理论以及市场分割理论。这三种理论是存在不同的解释，他们解释了不同形状的收益率曲线，回答了各种不同的国债即期利率存在差别的原因，并且这种差别体现不同的变化因期限的长短。

二、研究方法

（一）独立成分分析

ICA假设条件为：各独立成分属于统计独立；服从非Gaussian分布；并且以下混合矩阵均为可逆矩阵。若有k个时间序列，记为X1，X2，X3，…，Xk，则独立成分模型可表示为：X=As式中，X表示k个T时间序列的观察值，A为混合矩阵，S表示经混合矩阵分离前的独立成分向量，Si,s与Sj,t相互独立。通过计算A的逆矩阵W可以得到求解独立成分的公式：WX=s，金融市场的波动率X都按照一定的权重比例分配在每个独立成分中，即独立成分是对金融市场的观察值进行还原。矩阵S的元素，(i=1,2,…,k；t=1,2,…,T)通过上述公式可以看出系数wij的绝对值决定每个原始变量X。

（二）Nelson-Siegel利率期限结构模型

Nelson-Siegel模型的远期利率公式为：

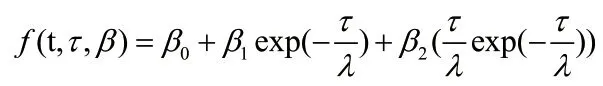
式中τ表示债券的到期期限，其中β=(β0,β1,β2)，λ为待估参数。β0，β1，β2对该函数图像有不同的影响。因子载荷数是主成分和各变量的相关系数，其值小于等于1。β0表示长期利率水平，β0是一个常数。随着到期期限τ的增大，即期利率y(τ)逐渐接近β0，当τ趋于无穷时，即期利率等于β0；β1是因子载荷数为的一个单调递减函数，随着变量τ的增大，逐渐变小并趋于0，因此可以看出β1对利率存在短期影响，且影响指数变化，速度较快；β2的因子载荷数为是一个先增后减函数，随着τ增大最终趋于0，因此β2介于β0和β1之间对利率存在中期影响。λ称为衰减率，影响短期项和中期项。

三、基于收益率预测的债券组合风险管理

上证国债组合分析

选取2019年发行国债收益率数据，该数据的选择对应短期国债、中期国债、长期国债，用于验证不同到期期限的国债所体现的风险对冲效果，数据来源中国债券信息网（见表1）。

表1

针对以上数据，利用R语言编程进行分析得出短、中、长期国债收益率分别对应的数据（见表2）。

表2

接下来对比两种模型下利率风险对冲误差为对冲组合收益与目标债券收益率的差，并对该对冲误差进行正态分布检验，得到表3结果（见表3）。

表3 利率风险对冲误差统计量

得出不论从误差均值还是绝对误差均值来看，DNS-ICA的值都小于DNS，这表现出给ICA的Nelson-Siegel宏观金融模型利率风险的对冲效果要优于传统的模型。

四、结语

利率期限结构是债券特有属性，而利率期限结构又是为了研究期限不同而其他特征相同的利率之间的关系。根据本文可以看出到期期限不同的债券所表现出的特征是有所不同，结合本文，对不同到期期限的国债收益率进行风险预测和稳定性判断，新模型较传统模型预测效果更好。